Similar presentations:
Разностные методы решения задач математической физики. Лекция 9
1.
Лекция 9Разностные методы решения задач математической физики
Уравнения математической физики
d 2U
dx
2
d 2U
dx
2
d 2U
dy
2
d 2U
dy
2
0
(1) уравнение Лапласа
x, y
(2)
уравнение Пуассона
c dT d 2T d 2T
k dt
dx 2 dy 2
(3) уравнение теплопередачи
d 2C d 2C
dC
D
2
2
dt
dy
dx
(4) уравнение диффузии
Некоторые области практического применения уравнений математической физики:
1) Моделирование технологических процессов микро- и наноэлектроники:
термический отжиг, диффузия примеси технология выращивания кристаллов,
ионно-плазменная и плазмохимическая обработка и др.
2) Моделирование характеристик электронной элементной базы: временных
параметров, частотно-спектральных характеристик, емкости и индуктивности
элементов микроэлектронной техники и др.
3) Расчет характеристик оптических элементов в микроисполнении: интегральнооптические и волоконно-оптические элементы, дифракционные элементы,
градиентные элементы, нанофотоника, плазмоника, метаматериалы и др.
4) Решение смешанных (мультифизических) задач: лазерная и ионно-плазменная
резка, сварка, закалка конструкционных сталей, магнитно-импульсная гибка
листовых материалов, термооптический расчет резонаторов мощных лазеров и др.
2.
Лекция 9Разностные методы решения задач математической физики
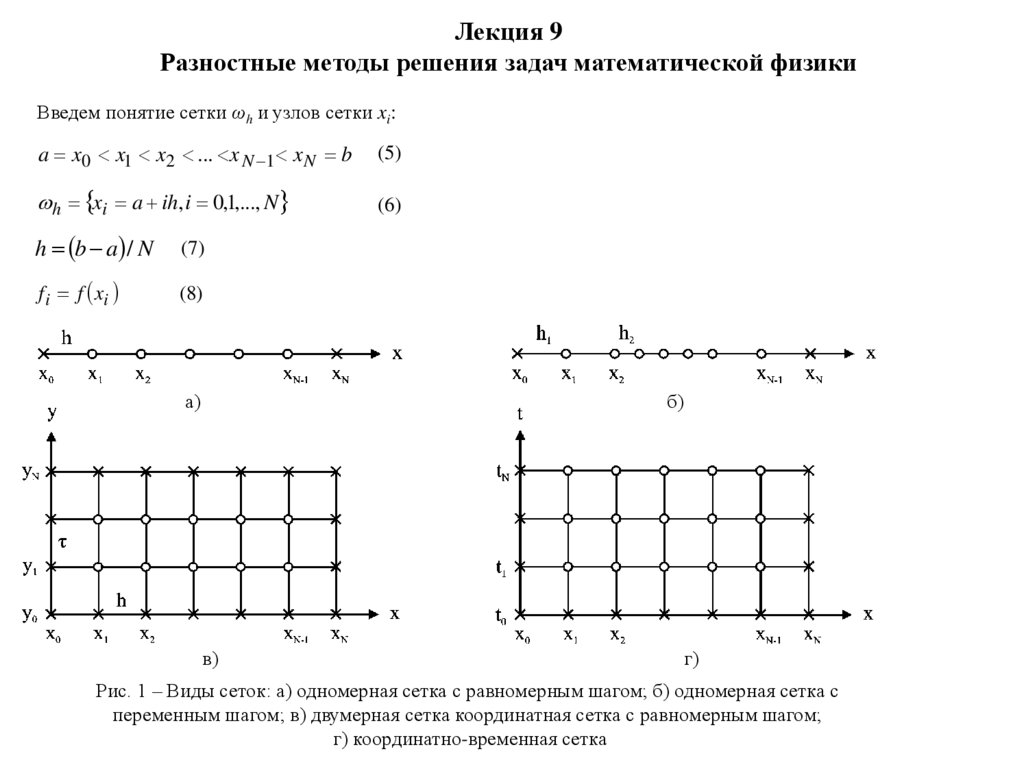
Введем понятие сетки ωh и узлов сетки xi:
a x0 x1 x2 ... x N 1 x N b
(5)
h xi a ih, i 0,1,..., N
(6)
h b a / N
(7)
f i f xi
(8)
а)
б)
в)
г)
Рис. 1 – Виды сеток: а) одномерная сетка с равномерным шагом; б) одномерная сетка с
переменным шагом; в) двумерная сетка координатная сетка с равномерным шагом;
г) координатно-временная сетка
3.
Лекция 9Разностные методы решения задач математической физики
Запишем производные 1-го порядка для искомой функции f(x):
прав
df
dx i
лев
df
dx i
центр
df
dx i
f xi 1 f x i f x i 1 f x i
x i 1 x i
h
f xi f xi 1 f xi f xi 1
xi xi 1
h
f xi 1 f xi 1 f xi 1 f xi 1
xi 1 xi 1
2h
(9)
правая производная
(10)
левая производная
(11)
центральная производная
Производную второго порядка определим как разность правой и левой производных первого
порядка, отнесенную к изменению аргумента:
d2 f
dx 2
прав
лев
df f xi 1 2 f xi f xi 1
1 df
dx i
h
dx
h2
i
i
Рис. 2 – Вычисление конечно-разностных
производных первого порядка функции cos(x)
(12)
4.
Лекция 9Разностные методы решения задач математической физики
Точность замены производной разностным выражением оценивается по формуле Тейлора:
лев
df
dx i
f xi f xi h
h
(13)
h2
(14)
f xT , xT x h; x
2
Следовательно, левая производная аппроксимируется с первым порядком точности:
f xi h f x hf x
лев
df
dx i
f x
h
f xT , xT x h; x
2
(15)
Аналогичным образом оценивается погрешность аппроксимации для правой и центральной производных:
прав
df
dx i
f x
центр
df
dx i
h
f xT , xT xi , xi 1
2
f x
(16)
h2
f xT , xT xi 1 , xi 1
6
(17)
Таким образом, погрешность замены производной конечно-разностным аналогом зависит от выбранного
шага сетки и гладкости функции.
Погрешностью разностной схемы называется разность между решением исходной задачи и ее решением в
конечно-разностном виде.
Устойчивостью разностной схемы называется свойство ограниченности полученного решения при любом
числе итераций / шагов решения. Если конечно-разностное решение неограниченно возрастает, начиная с
какой-либо итерации, схема является неустойчивой. Под условной устойчивой схемой понимают схему,
устойчивую на ограниченном числе итераций / шагов решения.
5.
Лекция 9Разностные методы решения задач математической физики
Рассмотрим линейное уравнение Лапласа, описывающее распределение электрического
потенциала в изотропной среде:
d 2U
dx
2
d 2U
dy
2
0
(18)
Перепишем частные производные второго порядка в конечно-разностном виде и
выразим искомый потенциал Ui,j:
1
U i, j U i 1, j U i 1, j U i, j 1 U i, j 1
(19)
4
Зададим нулевые начальные условия для внутренних узлов сетки:
U t 0 0
(20)
Зададим граничные условия для внешних узлов сетки:
U y 0 1В,
Ui , j 1, i 1..N , j 1
(21)
U y 10 0,
U i, j 0, i 1..N , j N
(22)
U x 0 0,
U i, j 0, i 1, j 1..N
(23)
U i, j 0, i N , j 1..N
(24)
U x 0 0
Рис. 4 – Конечно-разностное решение
двумерного линейного уравнения Лапласа
6.
Лекция 9Разностные методы решения задач математической физики
Рассмотрим уравнение Лапласа, описывающее распределение потенциала в изотропной среде:
Рис. 5 – Геометрия электродов Cr + Cu
на кристалле LiNbO3
Рис. 6 – Потенциалы электродов Cr + Cu
на кристалле LiNbO3
Рис. 8 – Электрическое поле в виде
линий равного потенциала
Рис. 9 – Цветовая карта распределения
напряженности электрического поля
Рис. 7 – Предварительный вариант
сетки (первая итерация)
Рис. 10 – Окончательный вариант
сетки (последняя итерация)
7.
Лекция 9Разностные методы решения задач математической физики
Особенности формирования неоднородностей:
1) Ориентированы вдоль полярной оси кристалла.
2) Зарождаются на отрицательных электродах.
3) Локализованы у краев (углов) электродов.
4) Имеют существенно отличающиеся размеры.
5) Исчезают при нагревании до 150-170°С.
Рисунок 11 – Иглообразные оптические неоднородности
поверхности кристалла ниобата лития: а) между электродами;
б) на краях электродов. Напряжение – до 650 В.
Исследование формирования и развития неоднородностей поляризационно-оптическим методом:
а)
б)
в)
г)
Рисунок 12 - Образование неоднородностей: а) U=0 В; б) U=625 В; в) U=650 В; г) U=650 В с выдержкой 60
сек; 1 – перераспределение поверхностного заряда полем Ey у торца электрода, 2 – начальный этап формирования
неоднородностей, 3 – скачкообразное увеличение неоднородностей, 4 – прорастание неоднородностей до
положительного электрода
8.
Лекция 9Разностные методы решения задач математической физики
Рисунок 13 – Локализация неоднородностей вблизи краев
отрицательных электродов
Рисунок 15 – Распределение электрического
поля в межэлектродном зазоре
Рисунок 14 – Образование неоднородностей
на микродефектах границ электродов
Рисунок 16 – Распределение напряженности
электрического поля Ez вблизи края электрода
9. Лекция 9 Основы численного интегрирования
Методы численного интегрирования основаны на замене определенного интеграла конечнойсуммой в виде произведения функции, зависящей от подынтегральной, на шаг изменения
дискретного аргумента.
а)
б)
в)
Рис.3. Численное интегрирование: а) метод правых прямоугольников; б) метод левых
прямоугольников; в) метод средних прямоугольников
b
n
b
n
f ( x)dx hf ( xi 1 )
f ( x)dx hf ( xi )
a
a
| P | M1
i 1
h b a
2
M1 max | f x |, x a; b
| P | M1
i 1
h b a
2
M1 max | f x |, x a; b
b
n
f ( x)dx
a
i 1
f ( xi 0.5 )h
h 2 (b a)
P M2
24
M 2 max f '' ( x)
x [ a, b]
10. Лекция 9 Основы численного интегрирования
Методы численного интегрирования основаны на замене определенного интеграла конечнойсуммой в виде произведения функции, зависящей от подынтегральной, на шаг изменения
дискретного аргумента.
а)
б)
Рис.4. Численное интегрирование: а) метод трапеций; б) метод парабол
xi
xi
x i 1
xi 1
xi 1
b
b
xi
a
f ( xi 1 ) f ( xi )
f ( x)dx
h
2
1
f ( x)dx h [ ( f 0 f n ) f1 ... f n 1 ]
2
h 2 (b a )
P
M2
12
M 2 max f '' ( x)
x [ a, b]
f ( x)dx
a
f ( x)dx
L2,i ( x)dx
h
( f i 1 4 f i 0,5 f i )
6
b a
[ f 0 f 2n 2( f 2 f 4 ... f 2n 2 )
6n
4( f1 f 3 f 5 ... f 2n 1 )]
h 4 (b a )
P
M4
2880
M 4 max f
x [ a,b]
IV
( x)










 mathematics
mathematics