Similar presentations:
Решение систем, содержащих показательные уравнения
1. Тема урока:
РЕШЕНИЕ СИСТЕМ,СОДЕРЖАЩИХ
ПОКАЗАТЕЛЬНЫЕ
УРАВНЕНИЯ.
2. Проверка домашнего задания.
3. Ответы к домашнему заданию.
4. Решить уравнения.
4 5 2 24 0x
x
2
x 1
3 2
x 1
5 2 6
3 16 2 81 5 36
x
x
x
x
5.
Решить уравнение:4 x 5 2 x 24 0
4 x ( 22 ) x 22 x ( 2 x ) 2 .
Нетрудно заметить, что
22 x 5 2 x 24 0
Введем новую переменную
t 2x
22 x t 2
t 2 5t 24 0
t1 8
t2 3
Вернемся к старой переменной, решив уравнения:
1) 2 x 8
2 x 23
x 3
2) 2 x 3
нет решений
(т.к. -3 < 0)
Ответ:
x 3
6.
Решить уравнение:2 x 1 3 2 x 1 5 2 x 6
Все показательные функции соберем в одной части, т.е. 5 2 x перенесем влево.
2 x 1 3 2 x 1 5 2 x 6
Вынесем за скобки общий множитель – степень с меньшим показателем: 2 x 1.
деления
2 x В 1(скобках
22 3 записывается
1 5 21 ) результат
6
на то выражение, что выносим за скобки, а
x при
1 делении показатели степеней
2 (4 3 10) 6
вычитаются.
x 1
2 ( 3) 6
Разделим обе части уравнения на (-3)
2 x 1 2, т.к. 2 21
x 1 1 x 2
Ответ:
x 2
7.
Решить уравнение:3 16 x 2 81x 5 36 x
Т.к. 36 x 0, можно обе части уравнения разделить на 36 x
16 x
81
) 2 ( )x 5
36
36
4
9
3 ( )x 2 ( )x 5
9
4
3 (
и выполнить сокращение
в скобках
Введем новую переменную t (
2
3t 5; 3t 2 5t 2 0
t
t1 1
4 x
)
9
9 x 1
( )
4
t
2
t2
3
Вернемся к старой переменной
4
1) ( ) x 1;
9
4
4
( ) x ( )0
9
9
x 0
Ответ:
x1 0; x2 0,5.
2)
4
2
( )x ;
9
3
2x 1
x 0,5
2 2x
21
( ) ( )
3
3
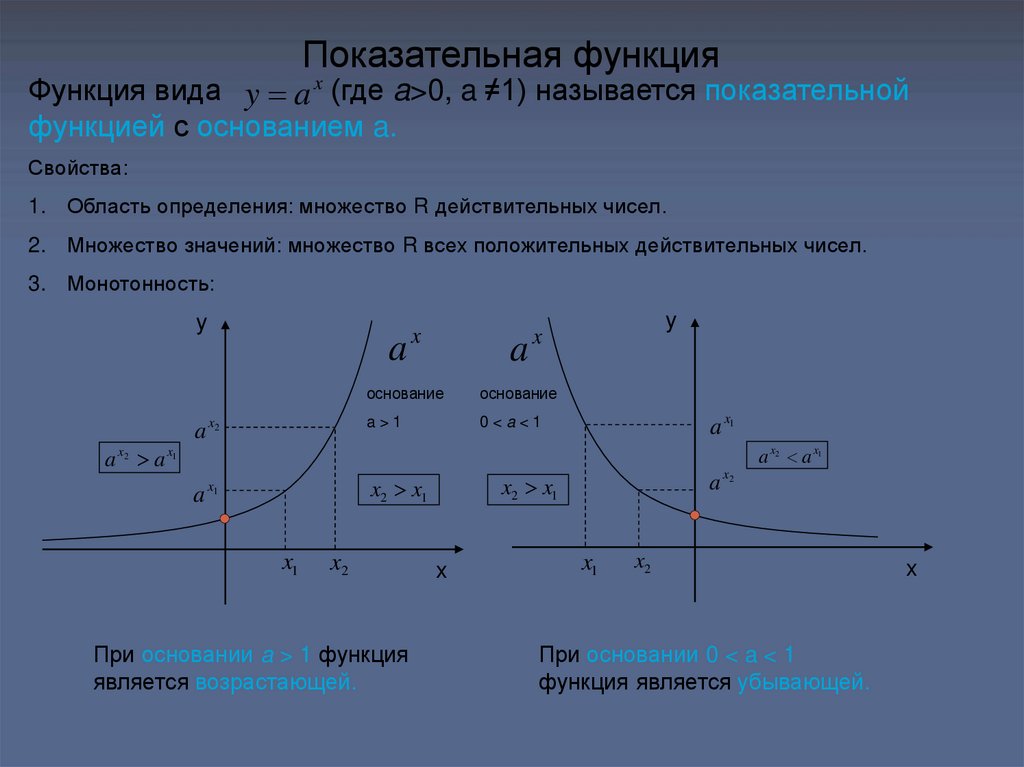
8. Показательная функция
Функция вида y a x (где a>0, a ≠1) называется показательнойфункцией с основанием a.
Свойства:
1. Область определения: множество R действительных чисел.
2. Множество значений: множество R всех положительных действительных чисел.
3. Монотонность:
y
x
a
основание
основание
a>1
0<a<1
a
a x2
y
x
a x1
a x2 a x1
a x2 a x1
a
x1
x2
При основании a > 1 функция
является возрастающей.
a x2
x2 x1
x2 x1
x1
x
x1
x2
При основании 0 < a < 1
функция является убывающей.
x
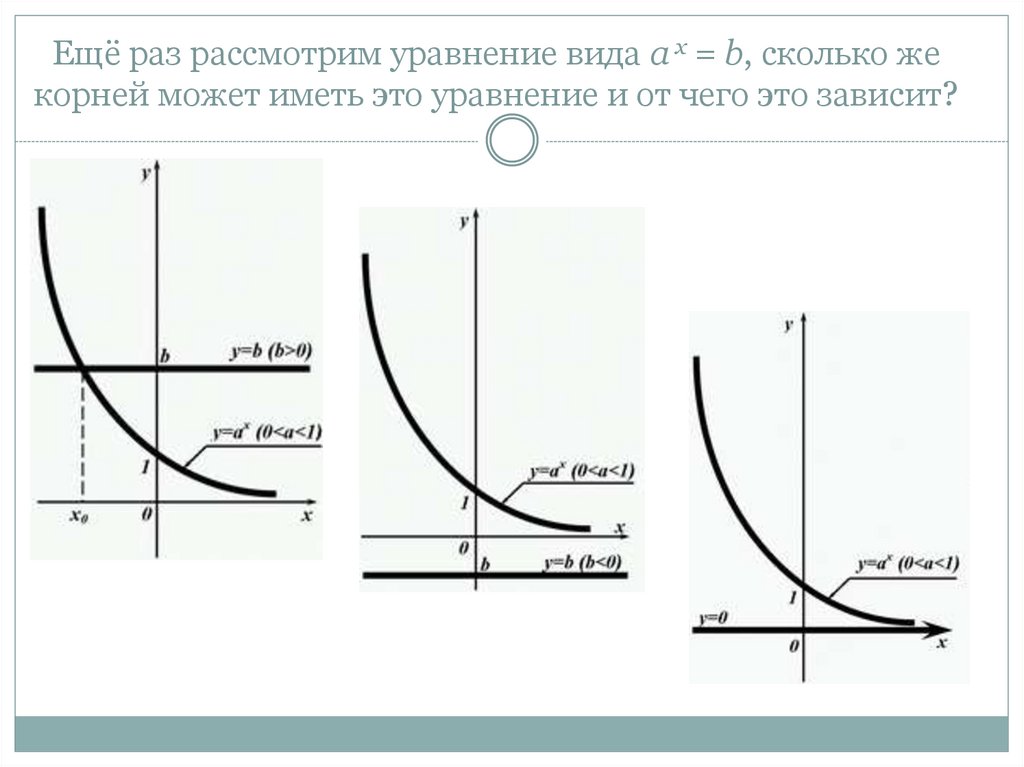
9. Ещё раз рассмотрим уравнение вида a х = b, сколько же корней может иметь это уравнение и от чего это зависит?
10.
Системы показательныхуравнений
Решить систему
x y 1
x 2 y 1
5
25
x 1 y
1 y 2 y
2
5
5
1 3 y 2
3 y 3
y 1 x 0
Ответ:
( 0;1).
Из первого уравнения выразим
x через y и подставим во второе
уравнение.
Решим второе уравнение,
найдем y.
Найдем вторую переменную,
подставив y = 1 в уравнение.
11.
Системы показательныхуравнений
Решить систему
27 x 3 y
x
3 81y 11
33 x 3 y
x
3 34 ( y 11)
Очевидно, что основанием обоих
уравнений является число 3.
Приводим обе части каждого
уравнения к одному основанию.
От системы показательных уравнений переходим к
системе уравнений:
3x y
x 4 y 44
Ответ: ( 4; 12 ).
3x y
x 12 x 44
y 12
x 4











 mathematics
mathematics








