Показательные уравнения и способы их решения

1.

Показательные
уравнения и способы их
решения.
Автор:
учитель математики МБОУ
«Средняя (полная)
общеобразовательная школа
№8» Елабужского
муниципального района РТ
Шурыгина И.В.

2.

Определение:
Показательные уравнения – уравнения, в
которых переменная входит только в
показатели степеней при постоянных
основаниях.
Например,
4
5
х 1
4,
х 2 3 х
0,5
х 7
5
3 х 8
,
1 2 х
0.5
2,
16 17 4 16 0.
х
х

3. Основные методы решения показательных уравнений

1.Метод уравнивания показателей.
2.Метод разложения на множители.
3. Метод введения новой
переменной.
4. Функционально-графический ( он
основан на использовании
графических иллюстраций или
каких-либо свойств функции).

4. Метод уравнивания показателей

f ( x)
g ( x)
Показательное уравнение a
a
, где a 0, a 1
равносильно уравнению
1 2 x 1 1
( )
,
2
8
1 2 x 1
1 3
( )
( ) ,
2
2
2 x 1 3,
2 x 3 1,
2 x 2,
x 1.
Ответ:х=1.
f ( x) g ( x),

5. Используя формулу

Решим уравнение
16 х
3 6
( ) ( ) ,
9
4
3 2 х
3 6
( )
( ) ,
4
4
2 х 6,
х 6 : ( 2),
х 3 .
Ответ: х=-3.
а n
b n
( ) ( )
b
a

6. Продолжим

16 х 3
125 2
( ) (
) ,
25
64
4 2 х 6 4 6
( )
( ) ,
5
5
2 х 6 6,
2 х 6 6,
2 х 12,
х 6.
Ответ: х=-6.

7. Решите уравнение и укажите промежуток, которому принадлежит корень уравнения

1 2 , 25 x 2
(
)
6.
36
1) ( 3; 2 2) 2;0
3) 2;5
4) 0;2
Решение:
(6 2 ) 2, 25 x 2 6;
1
4 4,5 x
1
2
6
,
6
6
;
т.к.
то получаем
36
4 4,5 x 1;
4,5 x 1 4;
4,5 x 3;
3
;
4,5
30
x
;
45
2
x
,
3
x
2
0;2
3

8. Решите уравнение, используя свойство пропорции. В ответе укажите меньший корень.

x2
6
22
8 5 x ,
2
3
6
x2
8 5 x
6 6
6
x 2 5 x 8
3 2 ,
2
2
62 ,
x 2 5 x 8 2,
x 2 5x 8 2 0,
x 2 5x 6 0,
x1 2
x2 3
Ответ:2-меньший корень.

9. Метод разложения на множители.

Решите уравнение 2 3x 1 6 3x 1 3 9,
3x 1 (2 32 6 31 ) 9,
x 1
3
9 9,
3x 1 1,
x 1
0
3
3 ,
x 1 0,
x 1.
Ответ:x=1.

10. Решите уравнения:

64 8 x 8 0,
2x
2x
8 (64 x) 0,
2x
т.к.8
2х
0, то
64 x 0,
x 64.
Ответ:х=-64.

11.

1 х
1 х 1
( ) ( )
30
5
5
Т.к. 0 а 1 , то вынесем за скобку степень с
наибольшим показателем
1
1
( ) х (1 ( ) 1 ) 30,
5
5
1 х
( ) (1 5) 30,
5
1
( ) х 6 30,
5
1
( ) х 5,
5
5 х 5,
х 1.
х 1.
Ответ:х=-1

12.

Найти корни показательного уравнения, указать
их сумму.
162 х 8 81х 3 2 х 24,
2 х 81х 8 81х 3 2 х 8 3,
81х 2 х 8 3 2 х 8 ,
2 8 81 3 0,
81х 2 х 8 3 2 х 8 0,
х
2х 8
х
или
х1 3.
х1 х2 3 0,25 3,25.
Ответ: 3,25.
81х 3,
34 х 3,
4 х 1,
х2 0,25.

13. Решите уравнение методом введения новой переменной

2 2 х 2 х 2 0;
Пусть 2 х t ,где t 0 ,тогда t 2 t 2 0
По теореме, обратной теореме Виета, получаем:
t t 2
t1 t 2 1,значит, t 2 не удовлетворяет условию t 0
1
Если
2
t 1,то
1
t2 1
2 x 1,
2 x 20 ,
x 0.
Ответ:х=0.

14. Решите однородное уравнение

3 22 х 6 х 2 32 х 0,
3 2 2 3 2 3 0 : (2 3 ),
2х
х
х
2х
х
х
2
3
3 ( ) х 1 2 ( ) х 0,
3
2
2 х
(
Пусть 3 ) t ,
1
3t 1 2 0 t ,
t
t 0 ,тогда
3t 2 t 2 0,
t1 1, не удовлетворяет условию t 0
2
t2 ,
3
2 х 2
2
Если t
,то ( 3 ) 3 ; х 1.
Ответ:х=1.
3

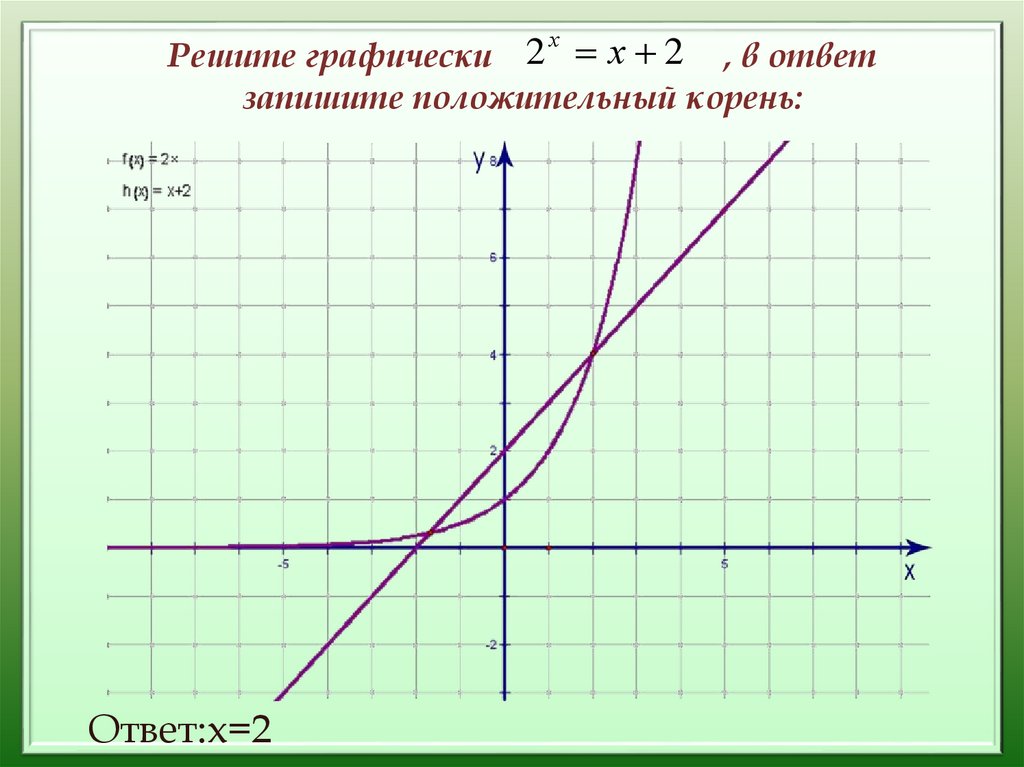
15. Решите графически , в ответ запишите положительный корень:

х
2
х 2
Решите графически
, в ответ
запишите положительный корень:
Ответ:х=2

16.

Уравнения, решаемые с помощью исследования
функций, входящих в левую и правую части
уравнения.
Решить уравнение
7 6 х х 2;
Рассмотрим функции:
у 7 6 х
6 х
у
7
Функция
- показательная, монотонно
и у х 2
убывающая на R.
Функция у х 2 -линейная,
монотонно возрастающая на R. Следовательно,
графики данных функций могут пересекаться не более
1 раза. Значит, уравнение не может иметь более
одного корня, который может быть найдет подбором:
х=5.
Ответ: х=5.

17.

Решим уравнение
5 х 12 х 13 х
Решение:
разделим левую и правую часть уравнения на 13 х ,
так как 13
х
0 , получаем
5
Рассмотрим функцию у
13
х
5
13
х
12
13
х
1.
х
12
,данная функция
13
монотонно убывает на множестве неотрицательных чисел, т.к.
является суммой двух убывающих показательных функций при
х 0.
Следовательно, данная функция принимает каждое свое
значение не более 1 раза, поэтому исходное уравнение имеет не
более 1 корня, который можно найти подбором.
2
2
2
Зная, что 5 12 13 , получаем
Ответ:
х 4.
х 2, х 4.

18.

Показательно-степенные уравнения вида
(a( x)) b ( x ) (a( x)) c ( x )
Данное уравнение эквивалентно уравнению а ( х ) 1 и системе:
в ( х) с( х),
а ( х) 0.
Отдельно рассматривается случай а( х) 0 при условиях
в ( х) 0, с( х) 0.
Решите уравнение
Решение:
3) х 2 0 при
( х 2) х 5 х ( х 2) 4 2 х .
2
1) х 2 1, х 3.
х 2.
х 2 5 х 4 2 х,
2) х 2 0,
х1 1, х2 4,
значит
х
0
.
При подстановке получаем при х=2 равенство
не имеет смысла.
х 4.
Ответ: 3;4.

19.

Решить показательное уравнение с параметром
Решить уравнение
2 а 10а 21 х 2 2 а а 15.
2
2
(а 2 10а 21) х 2а 2 а 15,
Разложим на множители квадратные трехчлены и получим:
(а 3)( а 7) х (2а 5)( а 3)
1. Если а 3, то 0 х 0, х R
2. Если а 7, то
3. Если
0 х 36, решений нет.
а 3, а 7, то х
Ответ: 1. При а 3,
2. При а 7,
2а 5
,
а 7
один корень.
х R.
нет решений.
3. При а 3, а 7, х
2а 5
,
а 7

20.

Литература:
Г.И.Ковалева и др. «Математика, тренировочные тематические
задания повышенной сложности с ответами», Волгоград, издательство
«Учитель»;
А.Г.Мерзляк, В.Б.Полонский, М.С.Якир «Алгебраический
тренажер», Москва, «Илекса» 2001г.;
И.С.Слонимская, А.И.Слонимский, «Математика, экспрессрепетитор для подготовки к ЕГЭ, уравнения и неравенства», Москва,
«АСТ Астрель» 2009г.;
Материалы из интернет-ресурсов.