Similar presentations:
Показательные уравнения и неравенства
1.
Тема:«Показательные
уравнения
и неравенства».
2.
«Развитие и образование ни одномучеловеку не могут быть даны или
сообщены. Всякий, кто желает к ним
приобщиться, должен достигнуть
этого собственной деятельностью,
собственными силами, собственным
напряжением».
А. Дистервег
3. 1. Какая функция называется показательной?
y a , где a 0, a 1x
4. 2. Какие из перечисленных ниже функций являются показательными?
1у 2
х
2
у х
2
3
у
3
4
да 5
у 2 3
х
нет
6
у х
1
да 7
у
х
да
х
да
нет
х
у 5х
нет
8
у 10
нет
5. Какое уравнение называется показательным?
af ( x)
a
g ( x)
, где a 0,a 1
6.
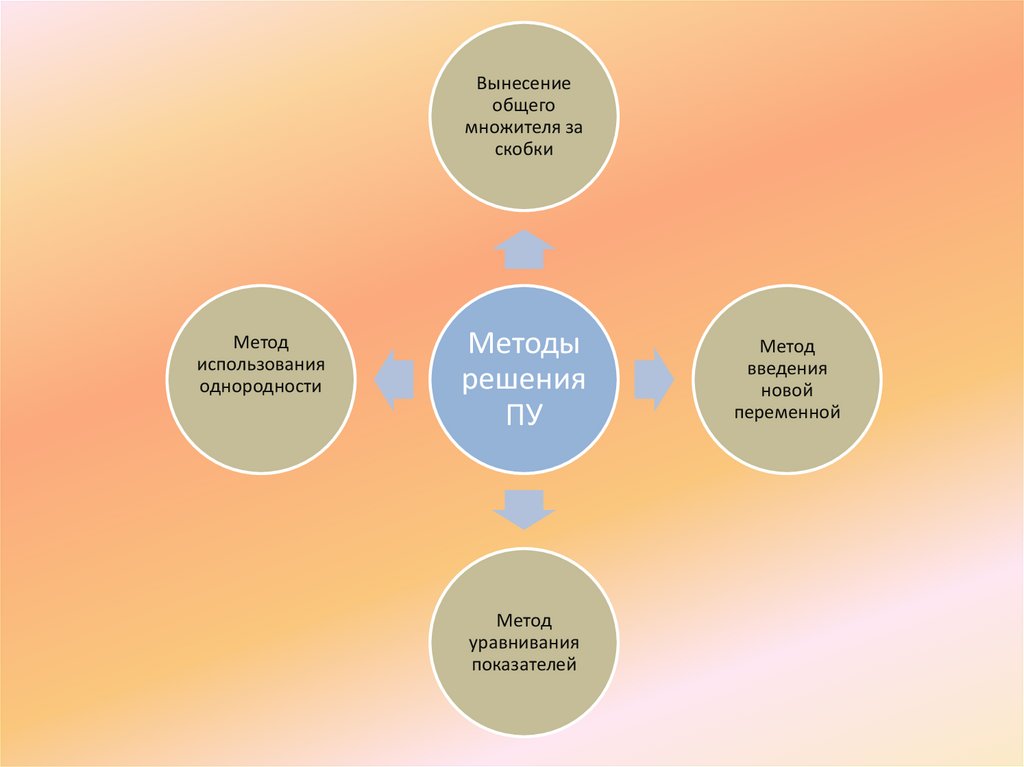
Какие основные методы
решения
показательных
уравнений существуют?
6.
Вынесениеобщего
множителя за
скобки
Метод
использования
однородности
Методы
решения
ПУ
Метод
уравнивания
показателей
Метод
введения
новой
переменной
7. Метод уравнивания показателей
1)5 5 , х 31)5 125
х
2) 2
3)3
3 х 6
2
х 1
3
х
8
4)8
5 х 8
5)11
х
3
3 х 6
1
2 ,3 х 6 1, х 2
3
2)2
1
3) Корней нет
х
4)8 81 , х 1, х 1
11
0
5)115 х 8 110 ,5 х 8 0, х 1,6
8. Вынесение общего множителя за скобки
x 23 72
x
2
3
x
3 (3 1) 72;
72
3 ;
8
x
3x 9;
3x 32;
x 2
Ответ: 2
9. Метод введения новой переменной
2x
1
x
4 5 4 4 0
1
x 2
1
x
(4 ) 5 4 4 0;
Пусть
1
x
4 t, t 0.
t 2 5t 4 0;
D 25 16 9;
t1 4, t2 1.
ОДЗ : x≠0
Вернемся кк
Вернемся
замене:
замене:
1
x1
1
4
4
x
1
1
x
4 1
0
x
x 1
решений _ нет
Ответ: 1
10.
Решение:4 x 2 x 1 3,
4 x 2 2 x 3 0,
Сделаем
Уравнение примет
1 замену переменных. Пусть
вид
у 2 2 y 3 0.
-3; 1
Полученное уравнение имеет корни
2 x 3,
x
2
11 x 0 .
Сделаем обратную замену: x
2 1
1
Ответ: 1
11.
Методвведения новой переменной
9
x 2 1
36 3
2( x 2 1)
3
x 2 3
9 4 3
3 0
x 2 3
3 0;
Вернемся к
замене:
3x 1 3 x 2 1 1
2
2
x 1
3
1
x 1 0
2
Пусть
x 2 1
3
t, t 0.
t 2 4t 3 0;
t1 3, t2 1.
x 0
x 0
x1 1
2
x 1 x 1
2
2
Ответ: 0,1,-1
12. Использование однородности
64 9 x 84 12 x 27 16 x 064 32 x 84 3x 4 x 27 4 2 x 0
Разделив обе части
уравнения на
42 x ,
получим:
Вернемся к
замене:
3
3
64 ( )2 x 84 ( )x 27 0
4
4
3 x 3
( 4 ) 4
( 3 )x 9
4
16
Пусть
3
( )x t, t 0.
4
64t 84t 27 0;
x 1
x 2
3
9
, t2 .
4
16
Ответ: 1 или 2
2
t1
13. Укажите методы решения показательных уравнений.
1.4.
2.
5.
3.
6.
Метод
уравнивания
показателей.
Функционально –
графический метод.
2, 6
1, 5
Метод введения
новой переменной.
3, 4
14. Какое неравенство называется показательным?
Какое неравенствопоказательным?
a
f ( x)
a
g ( x)
называется
, где a 0,a 1
15. Что нужно учесть при решении показательных неравенств ?
Решить неравенство 2x 12 x 20
x 0.
?
Что нужно учесть при решении простейших
показательных неравенств ?
1. Привести основания степени к одинаковому основанию
2. Использовать свойства монотонной функции
16. Решите неравенства
x8 x 3
8 x 3
3x 81
x R
x
3 x 34
4
2
9
3
x
2
2
2
3 3
x 2
x 4
Ответ:
x
Ответ: Х-любое
x ;4
Ответ:
; 4
4
x
x
2
x 2;
Ответ: 2;
17. Решите неравенство
125 x 3
5
5
2 x 3
5
3 x 1
1 3 x 1
5 2 x 6 5 3 x 1
2x 6 3x 1
2x 3x 1 6
x 5
-5
x 5;
x
Ответ:
5;
18. Решите неравенство
1x 5 x
7
7
x 2 5 x
7
7 6
6
2
x 2 5 x 6
x2 5x 6 0
( x 2) ( x 3) 0
+
2 x 3
2
x 2;3
_
2
3
+
3
x
Ответ:
2;3
19.
Решите неравенство0,36
7 x 1
2 x
1
7 x 1
2 x
0,36
0,360
7x 1
0
2 x
7 x 1 2 x 0
7 x 1 x 2 0
1
x 2
7
1
7
2
x
1
Ответ: ; 2
7
20.
Решите уравнения и неравенства.1) 2 2
x
3
x
1
1
2)
3 3
1
5)
6
x
36
3) 10
4
4)2
х 3
x 3
1000
2 28
х


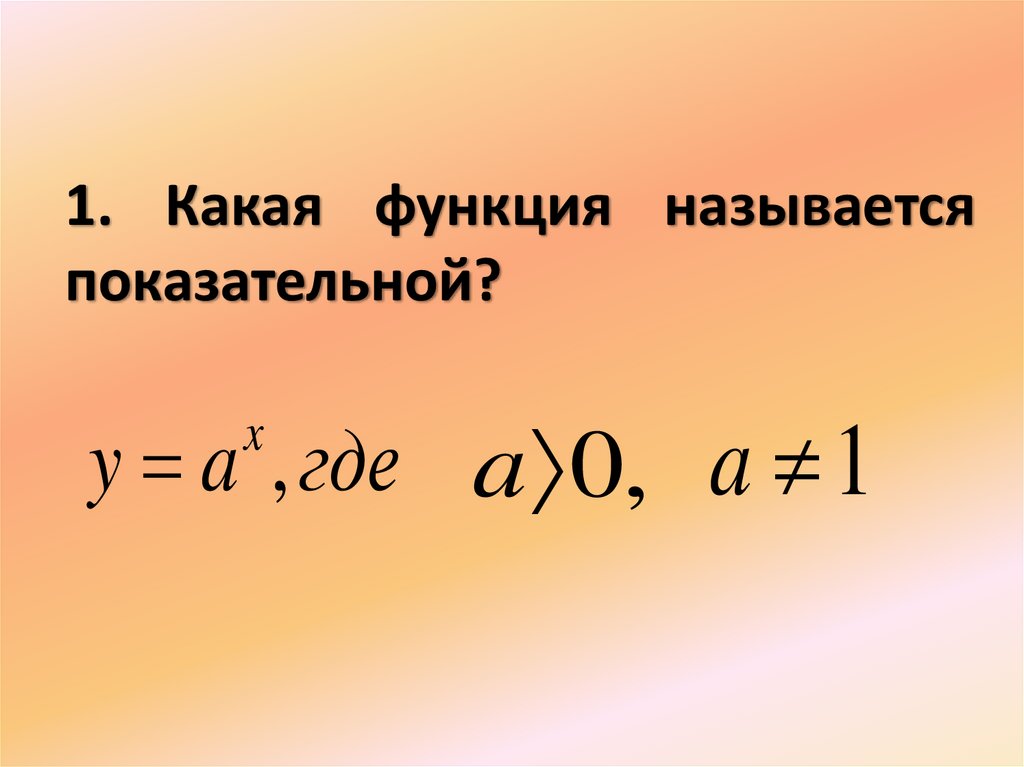









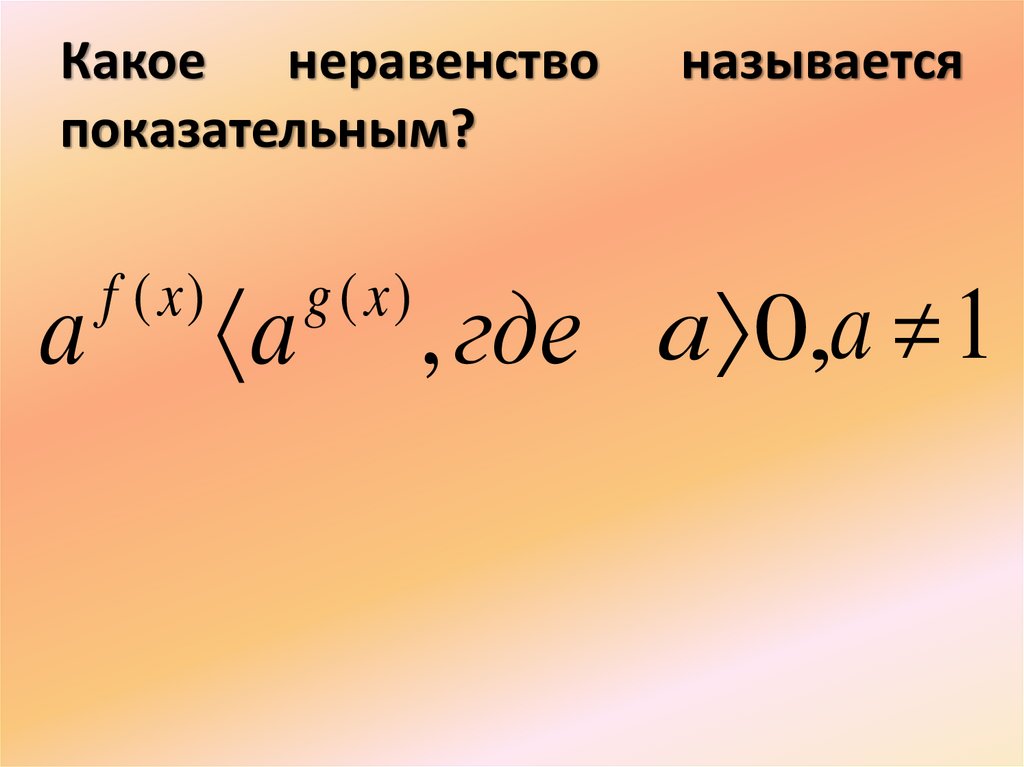






 mathematics
mathematics