Тригонометрические уравнения

1.

Тригонометрические
уравнения

2.

Тригонометрическое уравнение – это уравнение, в котором неизвестная находится
строго под знаком тригонометрической функции.
Существует два способа решения тригонометрических уравнений:
Первый способ – с использованием формул.
Второй способ – через тригонометрическую окружность.
Тригонометрическая окружность - это главный инструмент тригонометрии, она
позволяет измерять углы, находить их синусы, косинусы и прочее.

3.

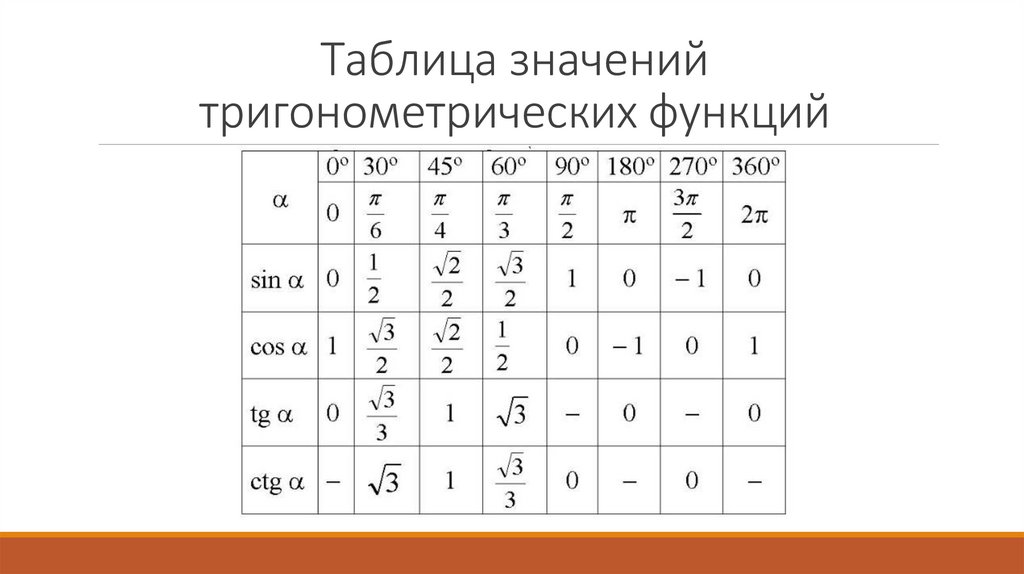
Таблица значений
тригонометрических функций

4.

Знаки тригонометрических функций

5.

Основные формулы тригонометрии
Основное тригонометрическое
тождество
Выражение тангенса через синус и
косинус
Выражение тангенса через синус и
косинус
Синус суммы и разности
Косинус суммы и разности
Тангенс суммы и разности

6.

Формулы приведения и их правила
1.Необходимо определить знак результата по таблице четвертей
2.Определить, изменяется ли наша функция на кофункцию.
Если присутствуют углы
, то происходит замена на кофункцию.
sin a-> cos a ; cos a -> sin a ; tg a -> ctg a ; ctg a -> tg a

7.

Формулы двойного аргумента
Формулы сложения верны для любых α и β , в том числе и для β =α . В этом случае получим
формулы синуса, косинуса и тангенса двойного аргумента, которые являются следствиями
формул сложения:

8.

Формулы тройного аргумента

9.

Формулы половинного аргумента

10.

Формулы преобразования суммы и
разности в произведение

11.

Пример
Решим уравнение:
Не подходит по условию
Возвращаемся к старой переменной sinx=1