Similar presentations:
Основные законы распределения ДСВ. Биномиальный, Пуассона
1. Основные законы распределения ДСВ. Биномиальный, Пуассона.
Урок 172. Фундаментальные условия схемы независимых испытаний.
1. Число опытов фиксировано и проходят водних и тех же неизменных условиях.
2. Каждый опыт приводит к одному из двух
взаимно исключающих исходов, которые
условно называют «УСПЕХ» и «НЕУДАЧА» это взаимно несовместные и
противоположные события.
3. Вероятность «успеха» p остается постоянной
от испытания к испытанию. Вероятность
«неудачи» – q.
4. Все испытания независимы.
3. Формула Бернулли
Вероятность того, что в n независимыхиспытаниях «успех» наступит ровно m раз,
равна
где p – вероятность «успеха» в каждом
испытании, а q = 1 – p,
и m = 0, 1, 2, …, n.
О случайной величине – число «успехов» в n
независимых испытаниях – говорят, что она
имеет биномиальное распределение с
параметрами n и p.
4. Задача 1
• В магазин поступила обувь с двух фабрик всоотношении 2:3. Куплено 4 пары обуви.
Найти закон распределения числа
купленных пар обуви, изготовленной первой
фабрикой. Найти математическое
ожидание и среднее квадратическое
отклонение этой случайной величины.
5. Задача 1
Дано:Испытание – случайным образом купить 4 пары
обуви.
Соотношение пар обуви 2-х фабрик 2 : 3.
Случайная величина X – число пар обуви,
изготовленной первой фабрикой из 4-х
купленных.
Найти: X, M(X), D(X).
6.
Пусть X – число пар обуви, изготовленнойпервой фабрикой из 4-х купленных.
Случайная величина может принимать
следующие значения: 0, 1, 2, 3, 4.
Случайная величина распределена по
закону Бернулли
Число испытаний n равно четырем.
Вероятность «успеха» - это вероятность
того, что пара обуви изготовлена первой
фабрикой.
7.
По условию поступила обувь с двухфабрик в соотношении 2:3.
Вероятность того, что случайно
выбранная пара обуви изготовлена
первой фабрикой, равна
p = 2 / (2 + 3) = 0,4, q = 1 – p = 0,6.
8.
x1 = 0, событие A1 – ни одна пара неизготовлена 1-й фабрикой.
P(X = 0) = P4 (0)=C40 p0 q 4 – 0= 1∙0.40∙0.64=0,1296
x2= 1, событие A2 – одна пара изготовлена 1-й
фабрикой
P(X = 1) =P4 (1)=C41 p1 q 4 – 1= 4∙0.41∙0.63= 0,3456
x3 = 2, событие A3 – две пары изготовлены 1-й
фабрикой
P(X = 2) =P4 (2)=C42 p2 q 4 – 2 =6∙0.42∙0.62 = 0,3456
9.
x4 = 3, событие A4 – 3 пары изготовлены 1-йфабрикой
P(X = 3) = P4 (3)= C43 p3 q 4 – 3 = 4∙0.43∙0.61= =
0,1536
x5= 4, событие A5 – 4 пары изготовлены 1-й
фабрикой
P(X = 4) = P4 (4)= C44p4 q 4 – 4 = 1∙0.44∙0.60 = =
0,0256
10.
Контроль:p1+ p2+ p3 + p4 + p5 = 0.1296 + 0.3456 + 0.3456 +
+ 0.1536 + 0.0256 = 1
xi
0
1
2
3
4
pi 0,1296 0,3456 0,3456 0,1536 0,0256
11.
xi0
1
2
3
4
pi 0,1296 0,3456 0,3456 0,1536 0,0256
По формуле М(Х) = x1 p1 + x2 p2 +…+ xn pn
М (Х) = 0 · 0,1296 + 1 · 0,3456 + 2 · 0,3456 +
+ 3 · 0,1536 + 4 · 0,0256 = 1,6
12.
xi0
1
2
3
4
pi 0,1296 0,3456 0,3456 0,1536 0,0256
По формуле
D (X) = M (X2) – (М (Х))2
M(X2)= 02 · 0,1296 + 12 · 0,3456 + 22 · 0,3456 +
+ 32 · 0,1536 + 42 · 0,0256 = 3,52
D (X) = M (X2) – (М (Х))2= 3,52 – 2,56 = 0,96.
13. Свойства биномиального распределения.
P ( Х m) C p qm
n
m
n m
Математическое ожидание
биномиального распределения равно
произведению числа испытаний на
вероятность «успеха» в каждом
испытании: M(X) = np.
Дисперсия равна: D(X) = npq.
14.
Случайная величина Х – число пар обувисреди четырех, изготовленных первой
фабрикой, имеет биномиальный закон
распределения с параметрами:
n = 4, p = 0,4.
Найдем математическое ожидание и
дисперсию случайной величины Х по
свойству биномиального распределения.
15.
Биномиальный закон распределения спараметрами n = 4, p = 0,4.
По свойству биномиального
распределения:
М (Х) = np = 4 ∙ 0,4 = 1,6,
D (X) = npq = 4 ∙ 0,4 ∙ 0,6 = 0,96.
Ответы совпадают.
Ответ: М(Х) = 1,6, D(Х) = 0,96.
16. Асимптотические формулы. Закон редких событий.
Закон распределения Пуассона:Формулу Пуассона применяют,
когда вероятность «успеха» очень
мала, а число испытаний велико.
При этом np ≤ 10.
17. Свойства распределения Пуассона
Математическое ожидание и дисперсияслучайной величины, распределенной по
закону Пуассона, совпадают и равны
параметру λ этого закона, т.е.
М (Х) = λ, D (Х) = λ, M(X) = D(X)
Таким образом, np = λ является
параметром распределения Пуассона.
18.
Задача № 2Среднее число инкассаторов, прибывающих утром на
автомобиле в банк в 15-ти минутный интервал,
равно 2. Прибытие инкассаторов происходит
случайно и независимо друг от друга.
1) Составьте ряд распределения числа инкассаторов,
прибывших утром на автомобиле в банк в течение
15 минут.
2) Найдите числовые характеристики этого
распределения.
3) Определите вероятность того, что в банк в
течение 15 минут прибудут на автомобиле хотя
бы два инкассатора.
4) Определите, чему равна вероятность того, что в
течение 15 минут число прибывших инкассаторов
окажется меньше 3-х.
19.
Дано: Испытание – инкассаторы прибывают утром наавтомобиле в банк в 15-ти минутный интервал.
Случайная величина X – число инкассаторов,
прибывающих утром на автомобиле в банк в 15-ти
минутный интервал
Среднее число инкассаторов, прибывающих в 15-ти
минутный интервал, равно 2.
Найти: а) X, б) M(X), в) D(X), г) P(X ≥ 2), д) Р(X < 3).
Решение:
Пусть случайная величина X – число инкассаторов,
прибывающих утром в банк: X = { 0, 1, 2, 3, 4, … , n }
По условию прибытие инкассаторов происходит
случайно и независимо друг от друга, следовательно,
возможны два взаимно исключающих исхода с одной и
той же вероятностью «успеха» в каждом испытании.
20.
Так же по условию известно, что среднеечисло инкассаторов, прибывающих утром
на автомобиле в банк в 15-ти минутный
интервал, равно 2.
Среднее значение случайной величины –
это ее математическое ожидание, оно
равно 2, следовательно, меньше 10.
Значит, случайная величина
распределена по закону Пуассона, с
параметром np = λ = 2.
21.
Если x = 0, то P(X = 0) = P0( 2 ) = 20 ∙ е – 2 /0 ! == 0,1353
Если x = 1, то P(X = 1) = P1( 2 ) = 21 ∙ е – 2 /1 ! =
= 0,2707
Если x = 2, то P(X = 2) = P2( 2 ) = 22 ∙ е – 2 /2 ! =
= 0,2707
Если x = 3, то P(X = 3) = P3( 2 ) = 23 ∙ е – 2 /3 ! =
= 0,1804
Если x = 4, то P(X = 4) = P4( 2 ) = 24 ∙ е – 2 /4 ! =
= 0,0902
22.
Если x = 5, то P(X = 5) = P5( 2 ) = 25 ∙ е – 2 /5 ! == 0,0361
Если x = 6, то P(X = 6) = P6( 2 ) = 26 ∙ е – 2 /6 ! =
= 0,0120
Если x = 7, то P(X = 7) = P7( 2 ) = 27 ∙ е – 2 /7 ! =
= 0,0034
Если x = 8, то P(X = 8) = P8( 2 ) = 28 ∙ е – 2 /8 ! =
= 0,0009
Если x = 9, то P(X = 9) = P9( 2 ) = 29 ∙ е – 2 /9 ! =
= 0,0002
23.
Если x = 10, то P(X = 10) = P10( 2 ) = 210 ∙ е – 2 /10 != 0.000038
Так как уже при x = 10 вероятность можно
принять равной нулю. Очевидно,
что P11 ( 2 ) еще меньше отличается от нуля.
Ряд распределения Х имеет вид:
Xi
0
1
2
3
4
Pi 0,1353 0,2707 0,2707 0,1804 0,0902
5
0,0361
6
0,0120
7
8
9
0,0034 0,0009 0,0002
24.
2) Числовые характеристики полученногораспределения случайной величины X известны из
условия.
Математическое ожидание и дисперсия случайной
величины, распределенной по закону Пуассона,
совпадают и равны параметру λ этого закона, т.е.
М (Х) = λ, D (Х) = λ
По условию среднее число инкассаторов,
прибывающих утром на автомобиле в банк в 15-ти
минутный интервал, равно 2. Значит M(X) = 2, а по
свойствам и D(X) = 2. Среднее квадратическое
отклонение равно корню квадратному из дисперсии,
то есть 1,4.
25.
3) Определим вероятность того, что в банк в течение 15минут прибудут на автомобиле хотя бы два
инкассатора.
«Хотя бы 2» - это «или 2, или 3, или 4, или 5, или …»
Тогда
P(X ≥ 2) = P(X = 2) + P(X = 3) + P(X = 4) + … + P(X = n)
С другой стороны, противоположным данному событию
будет событие (X< 2), то есть x ≤ 1, поэтому:
P(X ≥ 2) = 1 – P(X < 2) = 1 – ( P(X = 0) + P(X = 1)) =
= 1 – ( 0.1353 + 0.2707) = 1- 0.406 = 0.594
Вероятность того, что в банк в течение 15 минут
прибудут на автомобиле хотя бы два инкассатора,
составляет 0,594.
26.
4) Определим, чему равна вероятность того, что втечение 15 минут число прибывших инкассаторов
окажется меньше 3-х.
«Меньше 3-х» - это «или 0, или 1, или 2», тогда
Р(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) =
= 0.1353 + 0.2707 + 0.2707 = 0.6767
Вероятность того, что в течение 15 минут число
прибывших инкассаторов окажется меньше 3-х,
составляет 0,6767.
Ответ:
M(X) = 2, D(X) = 2, P(X ≥ 2) = 0,594, Р(X < 3) = 0,6767.
27. Распределение Пуассона
• Распределение Пуассона крайне важно вомногих физических и биологических задачах.
• Оно представляет собой грубую модель
частоты встречающихся катастрофических
наводнений при довольно длительном
периоде наблюдений.
• Распределение микроэлементов в образце
почвы может также приближаться к
пуассоновскому.
28. Радиоактивный распад
• Рассмотрим пробу радиоактивного вещества,которое в среднем дает r импульсов
радиоактивности в секунду.
• Ожидаемое число импульсов за t секунд есть
rt.
• Этот процесс можно описать
распределением Пуассона.
29.
• Проба состоит из очень большого числа nрадиоактивных атомов, причем каждый атом
имеет крайне малую вероятность p распада в
течение одной секунды.
• Ожидаемое число распадов за одну секунду
есть r = np.
• Ожидаемое число распадов за t секунд есть
rt = npt.
• Это является математическим ожиданием
распределения Пуассона, которое дает
вероятность k распадов за t секунд:
rt k rt
P(k )
e
k!
30. Подсчет клеток под микроскопом
• Предположим, что n клеток определенноготипа расположены случайным образом по
площади предметного стекла, которое
разбито квадратной решеткой на 900 (30 30)
равных участков.
• Вероятность того, что конкретная клетка
лежит в данном участке решетки, есть p =
1/900.
31.
• Процесс размещения n клеток на предметномстекле можно рассматривать как n повторных
испытаний для биномиального эксперимента,
где «успех» определяется как попадание
клетки в конкретный участок решетки.
• Если n велико, то для вычисления
вероятности того, что конкретный участок
решетки содержит k клеток, можно
воспользоваться пуассоновским
приближением биномиального
распределения: λ = np = n/900.
• Величина P(k) дает долю тех из 900 участков,
в которых содержится по k клеток.
32.
Задача № 3Стрелок может поразить мишень с вероятностью
0,9. Составить закон распределения числа
попаданий в цель при четырех выстрелах. Найти
среднее число попаданий при четырех выстрелах и
разброс значений числа попаданий для данного
стрелка при четырех выстрелах.
Дано: Испытание – четыре выстрела по мишени.
Событие А – мишень поражена
Р(А) = 0,9
Случайная величина X – число попаданий при
четырех выстрелах,
Найти: а) X, б) M(X), в) D(X).
33.
Решение:Случайная величина X - число попаданий в
цель при четырех выстрелах – может
принимать значения 0,1, 2, 3, 4
Соответствующие вероятности найдем по
формуле Бернулли:
P(X = m) = Pn(m) = Cnm p m q n – m.
Число испытаний n равно 4
Вероятность «успеха» - это вероятность того,
что стрелок попадет в цель - 0,9
Число «успехов» равно m, и меняется в
соответствии со значениями случайной
величины.
34.
x1 = 0, событие A0 – ни одного попадание причетырех выстрелах.
P(X = 0) = P4 (0)= C40 p0 q 4 – 0 = 1∙0.90∙0.14 =
= 0,0001
x2= 1, событие A1 – одно попадание при
четырех выстрелах.
P(X = 1) = P4 (1)= C41 p1 q 4 – 1 = 4∙0.91∙0.13 =
= 0.0036
x3 = 2, событие A2 – два попадания при
четырех выстрелах.
P(X = 2) = P4 (2)= C42 p2 q 4 – 2 = 6∙0.92∙0.12 =
= 0,0486
35.
x4 = 3, событиеA3 – три попадания при
четырех выстрелах.
P(X = 3) = P4 (3)= C43 p3 q 4 – 3 = 4∙0.93∙0.11 =
= 0.2916
x5= 4, событие A4 – четыре попадания при
четырех выстрелах.
P(X = 4) = P4 (4)= C44p4 q 4 – 4 = 4∙0.94∙0.10 =
= 0,6561
Контроль:
p1+ p2 + p3 + p4 + p5 = 0.0001 + 0.0036 + 0.0486 +
+ 0.2916 + 0.6561 = 1
36.
И так искомый закон распределения имеет вид:Xi
0
1
2
3
4
Pi 0.0001 0.0036 0.0486 0.2916 0.6561
Найдем среднее число попаданий при
четырех выстрелах.
По свойству биномиального распределения
математическое ожидание биномиального
распределения равно произведению числа
испытаний на вероятность «успеха» в каждом
испытании: M(X) = np.
Тогда M(X) = np = 4∙0,9 = 3,6 – среднее число
попаданий при четырех выстрелах.
37.
Разброс значений числа попаданий дляданного стрелка при четырех выстрелах – это
дисперсия случайной величины.
Для биномиального распределения дисперсия
равна
D(X) = npq.
Тогда D(X) = npq = 4∙0,9∙0,1 = 0,36, а среднее
квадратическое отклонение равно корню
квадратному из дисперсии и равно 0,6.
Значит, в среднем при четырех выстрелах
попаданий будет от трех до четырех.
Ответ: среднее число попаданий при четырех
выстрелах будет равно от трех до четырех.
38.
• Задача № 4• Дана случайная величина, распределенная
по закону редких событий, число вызовов на
АТС в минуту. Известно, что среднее число
вызовов в минуту на АТС равно 2.
• Найти вероятность того, что за 4 минуты на
АТС поступит 3 вызова, менее 3-х вызовов,
не менее 3-х вызовов.
39.
• Задача № 5Для того чтобы проверить точность своих
финансовых счетов, компания регулярно
пользуется услугами аудиторов для
проверки в бухгалтерских проводках
счетов. Предположим, что служащие
компании при обработке входящих счетов
допускают примерно 5% ошибок. Аудитор
случайно отбирает 4 входящих документа.
Найти закон распределения числа ошибок
выявленных аудитором.
Найти математическое ожидание и
среднее квадратическое отклонение этой
случайной величины.
40. Домашнее задание
• Решить задачи № 3, 4, 5Калинина
• Конспект: глава 6 § 6.3, 6.4
• Повторить: глава 4 «Повторение
испытаний»




















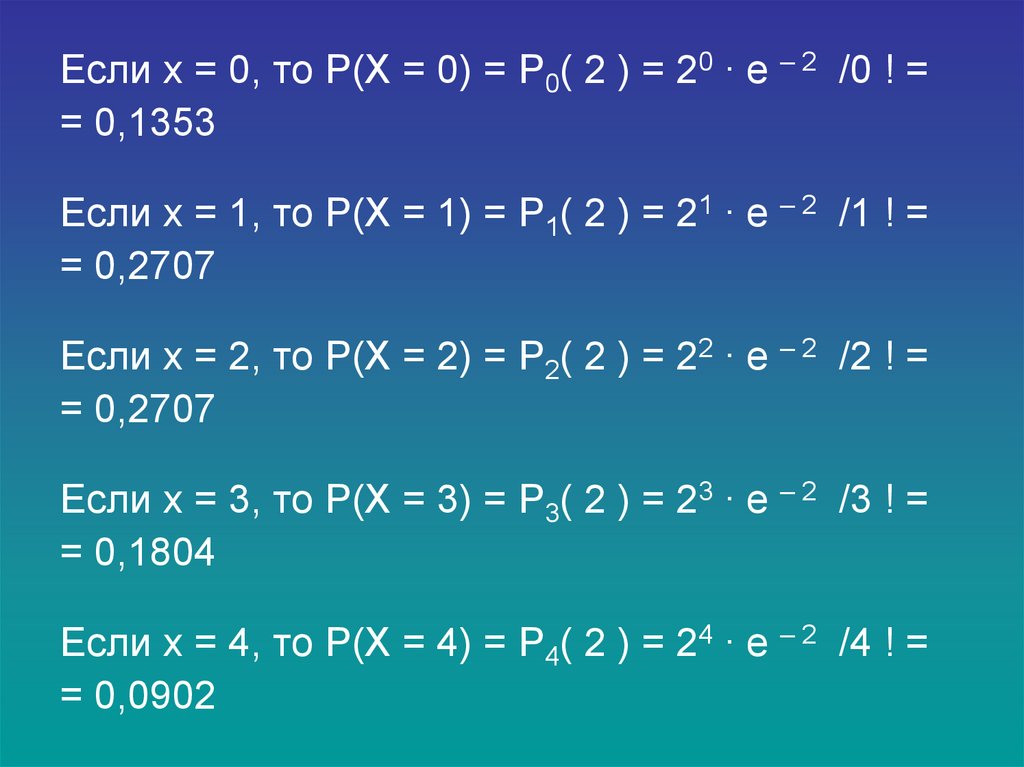



















 mathematics
mathematics








