§ 2. Многочлены над полем действительных чисел

1. Сопряжённые корни и неприводимые многочлены

1.71M

Category: $mathematics$ mathematics

Многочлены над полем действительных чисел

1. АЛГЕБРА (4-й семестр)

2023-24
учебный год

2. МНОГОЧЛЕНЫ НАД ЧИСЛОВЫМИ ПОЛЯМИ

ЛЕКЦИЯ 9

3. § 2. Многочлены над полем действительных чисел

Основными задачами этого раздела
являются рассмотрение вопросов:
1. Сопряжённые корни многочленов
2. Неприводимые над R многочлены
3. Отделение действительных корней
многочлена и метод Штурма

4. 1. Сопряжённые корни и неприводимые многочлены

Для комплексного числа z сопряжённым будет
число z , если:
z x iy
z x iy
Пользуясь свойствами сопряжённости, которые
можно распространить на любого число
слагаемых и сомножителей, для любого
многочлена с действительными коэффициентами
n
n 1
f
(
z
)
a
z
a
z
a1 z a0
имеем:
n
n 1
n
f ( z ) a n z a n 1 z
n 1
a1 z a0 f ( z )
(1)

5.

1. Сопряжённые корни и неприводимые многочлены
Теорема 1. Если комплексное число
z0=x0+iy0 является корнем многочлена
f(z)=anzn+an-1zn-1+…+a1z+a0 с
действительными коэффициентами, то и
сопряженное к нему число ž0=x0–iy0 также
является корнем этого многочлена.
◘ Пусть z0 – корень f(z). Тогда
f(z0)=anz0n+an-1z0n-1+…+a1z0+a0
и, следовательно, f ( z0 ) 0 . Но в силу (1)
n
n 0
n 1
n 1 0
f ( z0 ) a z a z a1 z 0 a0 f ( z 0 ) 0
т.е., ž0 – корень многочлена f(z). ◙

6.

1. Сопряжённые корни и неприводимые многочлены
Теорема 2. Неприводимыми над полем R являются
лишь многочлены первой степени и второй степени с
отрицательным дискриминантом.
◘ Пусть p(x) - любой неприводимый многочлен из R[x],
степень которого n>1. Достаточно доказать, что его
степень равна 2.
Пусть z0 - любой корень многочлена p(x). Этот корень не
может быть действительным, так как в противном
случае имели бы p(x)=(x-z0)q(x), где q(x) – многочлен
положительной степени из R[x], т.е. p(x) был бы
приводим над полем R.
Итак, z0 – мнимый корень и тогда (по теореме 1) ž0 тоже
является корнем многочлена p(x). Значит,
p( x) ( x z0 ) ( x z 0 ) q( x) x2 ( z0 z 0 ) x z0 z 0 q( x)

7.

1. Сопряжённые корни и неприводимые многочлены
p( x) ( x z0 ) ( x z 0 ) q( x) x2 ( z0 z 0 ) x z0 z 0 q( x)
Многочлен в квадратных скобках
принадлежит R[x], так как числа z0+ž0 и z0ž0 –
действительные.
А поскольку p(x)єR[x], по теореме о делении
с остатком частное q(x) тоже принадлежит
R[x].
В силу неприводимости p(x) многочлен q(x)
обязан иметь нулевую степень и,
следовательно, p(x) имеет вторую степень.
Понятно, что в этом случае дискриминант
многочлена p(x) отрицателен. ◙

8.

1. Сопряжённые корни и неприводимые многочлены
Следствие 1. Любой многочлен f(x)єR[x]
разлагается в произведение неприводимых
над полем R многочленов 1-ой и 2-ой
степени (или только первой, или только
второй):
k
m
i 1
k 1
f ( x) a ( x i ) ( x bk x ck )
2
◙

9.

1. Сопряжённые корни и неприводимые многочлены
k
m
i 1
k 1
f ( x) a ( x i ) ( x 2 bk x ck )
Очевидно, каждому линейному множителю
соответствует действительный корень f(x), а
каждому множителю 2-ой степени – пара
сопряженных мнимых корней.
Отсюда заключаем, что многочлен из R[x]
может иметь только чётное число мнимых
корней.

10.

1. Сопряжённые корни и неприводимые многочлены
Следствие 2. Многочлен нечётной степени
с действительными коэффициентами
имеет по крайней мере один
действительный корень.
◘ Мнимых корней – чётное число, значит
действительных – нечётное, т.е. хотя бы
один, так как всего корней – нечётное число.
◙

11.

1. Сопряжённые корни и неприводимые многочлены
Пример 1. Многочлен f(x)=x5+6x-9
Приводим?
приводим
над полем R,
так как имеет по крайней мере один
Почему?
действительный корень.
Пример 2. Многочлен f(x)=4x6+9x2+1
неприводим
над полем R,
Приводим?
так как не имеет действительных корней,
Почему?
ведь f(x)>0 при любом
xєR.

12. 2. Отделение действительных корней

Уравнения степени выше 4 неразрешимы в
радикалах. Поэтому большую роль играют
приближенные методы решения алгебраических
уравнений. Обычно при этом выделяют 3 этапа:
Нахождение границ действительных корней, т.е.
указание такого промежутка (a,b), в котором
находятся все действительные корни многочлена.
Отделение корней, т.е. нахождение таких
интервалов (ai,bi), в каждом из которых лежит
только один действительный корень.
Приближенное вычисление самих корней, т.е.
построение последовательности, сходящейся к
тому или иному корню.
Мы рассмотрим только два этапа.

13. 2. Отделение действительных корней

Лемма 1. (О модуле старшего члена). Если
f(z)=anzn+an-1zn-1+…+a1z+a0 – многочлен
степени n 1 из кольца C[z] и
A=max{|a0|,|a1|,…,|an-1|}, то при любом K R+
из неравенства
A
z K
1
an
(2)
вытекает неравенство:
an z
n
K a0 a1 z a n 1 z
n 1
(3)

14. 2. Отделение действительных корней

◘ Имеем:
a0 a1 z an 1 z
n 1
a0 a1 z ... an 1 z
A 1 z ... z
n 1
A z 1
z 1
n
n 1
Отсюда при |z|>1 для любого K R+ получаем, что
n
K a0 a1 z an 1 z
n 1
z
KA
z 1
(4)
A
z K
1
an
b1 1 q n
Sn
1 q
A max( a0 , a1 ,..., an 1 )

15. 2. Отделение действительных корней

n
K a0 a1 z an 1 z
n 1
z
KA
(4)
z 1
С другой стороны, имеем цепочку
равносильностей:
KA
z
n
z 1
an z
n
KA
an
z 1
(5)
KA
z 1
an
KA
z
1
an

16. 2. Отделение действительных корней

A
z K
1 (2)
an
n
z
n 1
K a0 a1 z an 1 z KA
z 1
Таким образом, если неравенство (2)
выполнено, то ввиду цепочки (5), имеем:
a n z KA
n
(4)
z
n
z 1
Тогда в силу (4) получаем требуемое:
a n z n K a0 a1 z a n 1 z n 1
◙

17. 2. Отделение действительных корней

Покажем способ применения леммы для
нахождения границ действительных корней
многочлена f(x)=anxn+an-1xn-1+…+a1x+a0 R[x].
A
1
По лемме имеем: если x
an
тогда
a n x n a n 1 x n 1 ... a1 x a0
где A max( a0 , a1 ,..., an 1 )
Следовательно, при таких x
f ( x) an x n an 1 x n 1 a0 0
f ( x) 0

18. 2. Отделение действительных корней

Отсюда следует, что все действительные корни
f(x) находятся в промежутке (–M,M), где
A
M
1
an
Таким образом мы указали один из способов (не
самый точный) для нахождения границ
действительных корней.
Пример 3. Найти границы действительных
корней многочлена f(x)=2x5 – 3x2 + 6.
Имеем A = 6, |a5| = 2, M = 6/2 + ?1 = 4.
Таким образом, все действительные корни f(x)
находятся в промежутке (–4,4). ◙

19. 2. Отделение действительных корней

Существует много способов отделения
действительных корней многочлена f(x) с
действительными коэффициентами.
Один из этих способов – графический –
заключается в том, что используя аппарат
математического анализа, исследуют функцию
f(x) и приближенно рисуют её график. При этом
возникает возможность указать приближенно и
промежутки, в которых находятся корни.
Разумеется, используя этот метод, мы не
гарантированы от ошибок.

20. 2. Отделение действительных корней

Наиболее безупречным в теоретическом
отношении является метод Штурма, имеющий
чисто алгебраический характер. Изложим суть
этого метода (без доказательства основной
теоремы Штурма).
Рассмотрим некоторую систему чисел,
например, 2, –7, –11, 13, –14. Здесь знаки
чередуются следующим образом: +, –, –, +, – .
Число перемен знаков в этой системе равно 3.
Если в системе встречается нуль, то он не
принимается во внимание (не имеет знака).
Например, в системе 3, –2, 0, 0, –3, 0, 5 число
перемен знаков равно 2.

21. 2. Отделение действительных корней

Применим к многочлену f(x) и его производной
f’(x) алгоритм Евклида, но при этом остатки
будем брать с противоположными знаками:
f ( x) f ' ( x) q1 ( x) f 2 ( x)
'
f ( x) f 2 ( x) q 2 ( x) f 3 ( x)
f 2 ( x) f 3 ( x) q3 ( x) f 4 ( x)
f m 2 ( x) f m 1 ( x) q m 1 ( x) f m ( x), f m ( x) НОД f ' , f .

22. 2. Отделение действительных корней

Система многочленов
f ( x), f ' ( x), f 2 ( x), , f m ( x)
(6)
называется системой функций Штурма для
многочлена f(x).
В дальнейшем будем рассматривать только
многочлены, не имеющие кратных корней.
Известно, что такие многочлены взаимно просты
со своей производной и поэтому fm(x)=c (const).
Обозначим через w(a) число перемен знаков в
системе чисел:
'
f (a ), f (a ), f 2 (a ), , f m

23. 2. Отделение действительных корней

Теорема Штурма.
Покажем
примере,
как, используя
теорему
Если на
a<b,
то w(a)
w(b) и число
Штурма, можно определить корни многочлена.
действительных
корней многочлена f(x)
Замечание. Многочлены ряда Штурма можно
с точностью
до положительных
внаходить
промежутке
[a,b]
равно w(a) – w(b).
множителей, т.е., при вычислениях можно
умножать и делить многочлены на числа, но
только на положительные, так как знак
многочленов играет в этом методе
существенную роль.

24. 2. Отделение действительных корней

Пример 4. Отделить действительные корни
многочлена f(x)=x3 – 10x + 2.
◘ M = A / |an| + 1 = 10/1 + 1 = 11.
Т.образом, корни находятся в промежутке (-11,11).
Далее находим производную f’(x)=3x2 – 10.
Затем применяя алгоритм Евклида, находим
| 10 x 3
систему многочленов Штурма: 3x 2 10
x 3 10 x 2 | 3x 2 10
30 x 2 100 || 3 x 9
30 x 2 9 x
9 x 100
3x 3 10 x
90 x 1000
20 x 6
90 x 27
973
Таким образом, ряд функций Штурма:
3x 3 30 x 6 || x
x3–10x+2, 3x2–10, 10x–3, 1.

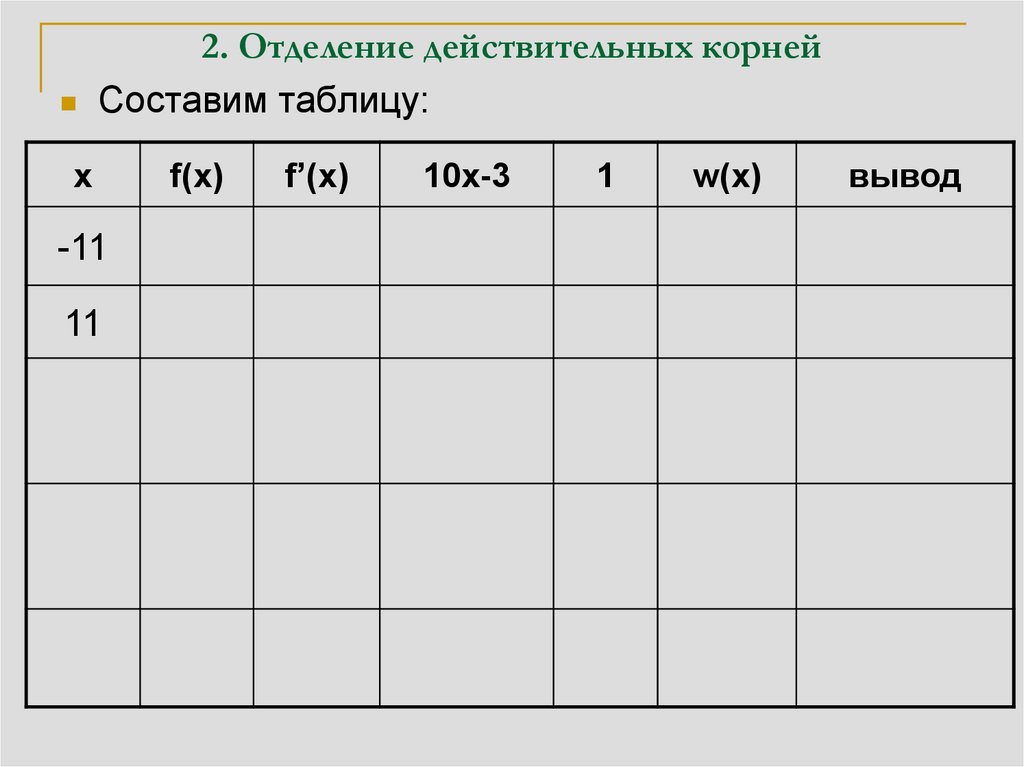
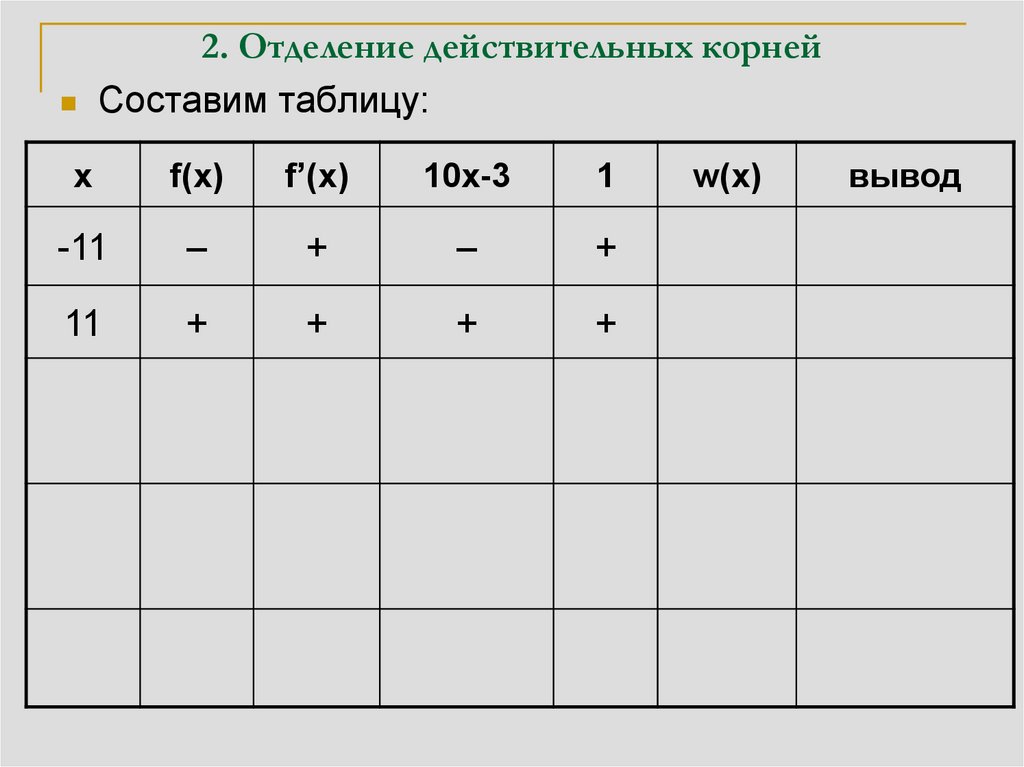
25. 2. Отделение действительных корней

Составим таблицу:
x
f(x)
f’(x)
10x-3
1
w(x)
вывод
-11
–
+
–
+
3
На интервале
(-11,11) есть три
0
действительных
корня
2
На интервале
(-11,0) есть один
корень, а на (0,11)
есть два корня
0
На интервале
(0,5) есть два
корня, а на (5,11)
корней нет
1
На интервалах
(0,3) и (3,5) есть
по одному корню
11
0
5
3
+
+
+
–
+
–
+
+
+
–
+
+
+
+
+
+

26. 2. Отделение действительных корней

27. 2. Отделение действительных корней

28. 2. Отделение действительных корней

29. 2. Отделение действительных корней

Составим таблицу:
x
f(x)
f’(x)
10x-3
1
w(x)
вывод
-11
–
+
–
+
3
11
+
+
+
+
0
На интервале
(-11,11) есть три
действительных
корня
0
5
3
+
+
–
–
+
+
–
+
+
+
+
+
2
На интервале
(-11,0) есть один
корень, а на (0,11)
есть два корня
0
На интервале
(0,5) есть два
корня, а на (5,11)
корней нет
1
На интервалах
(0,3) и (3,5) есть
по одному корню

30. 2. Отделение действительных корней

31. 2. Отделение действительных корней

32. 2. Отделение действительных корней

33. 2. Отделение действительных корней

34. 2. Отделение действительных корней

35. 2. Отделение действительных корней

36. 2. Отделение действительных корней

Таким образом, корни находятся на промежутках
(–11,0), (0,3), (3,5). Можно сузить эти промежутки,
учитывая, что на концах промежутка, имеющего
корни, f(x) принимает значения с
противоположными знаками:
f(–5)= –125+50+2<0,
f(0)>0 – корень принадлежит (–5,0);
f(–3)= –27+30+2>0 – корень принадлежит (–5,–3);
f(–4)=–64+40+2<0,
f(–3)>0 – корень принадлежит (–4,–3).
◙

English Русский Rules