Similar presentations:
Комплексные функции и многочлены
1. Математика Часть 2
УГТУ-УПИ2007 г.
2.
Лекция 4Комплексные функции и
многочлены.
1. Комплексная функция действительного
аргумента.
2. Многочлены в комплексной области.
3.
1.Комплексная функция действительного аргумента.
Если
Если каждому
каждому действительному
действительному числу
числу tt ставится
ставится вв
соответствие
соответствие комплексное
комплексное число
число z,z, то
то zz == z(t)
z(t) называется
называется
комплексной
комплексной функцией
функцией действительного
действительного аргумента.
аргумента.
4.
В алгебраической форме z(t) выглядит так:z (t ) x(t ) iy (t )
5.
Числу z (t ) соответствует вектор с координатамиx (t ), y (t ),следовательно, задание функции z (t )
равносильно заданию векторной функции скалярного
аргумента.
Отсюда, в частности, следует правило
дифференцирования комплексной функции:
z '(t ) x '(t ) iy '(t )
6.
z eПример:
i
- комплексная функция
действительного аргумента
z ' ?
Решение.
z ' ie
i
действительно,
z cos i sin ;
z ' sin i cos
i (cos i sin ).
.
7.
2. Многочлены в комплексной области.Рассмотрим многочлен порядка n:
f n ( z ) a0 a1 z a2 z ... an z .
2
n
Здесь
a0 , a1 , a2 ,..., an
заданные комплексные числа,
z - комплексная переменная.
Другой многочлен
m ( z ) b0 b1 z b2 z ... bm z .
2
m
8.
Рациональной дробью называется отношениедвух многочленов
f n ( z ) a0 a1 z a2 z ... an z
.
2
m
m z b0 b1 z b2 z ... bm z
2
При
при
n m
n m
n
дробь называется правильной,
- неправильной.
9.
Пустьm n.
Как и в элементарной алгебре справедливо
основное свойство деления:
Rp ( z)
fn ( z)
Ql ( z )
m ( z )
m ( z )
Здесь:
Ql (z ) - частное (целая часть дроби),
R p (z ) - остаток,
Ql ( z ), R p ( z ) - многочлены,
l m n
p m
10.
ЕслиR p (z ) 0
fn ( z)
Ql ( z )
m ( z)
или
f n ( z ) Ql ( z ) m ( z )
( деление без остатка)
Корни многочлена
Корнем
Корнем многочлена
многочлена f n (z ) называется
называется число
число
удовлетворяющее
удовлетворяющее уравнению
уравнению
f n ( z) 0
z0
,,
11.
В развернутом виде:a0 a1 z a2 z ... an z 0
2
n
Такое уравнение называется алгебраическим
уравнением n-ой степени.
Теорема Безу.
Т
Остаток, получаемый при делении
f n (z )
на (z-а), равен
f n (а )
fn ( z)
f n (a)
Ql ( z )
.
z a
z a
12.
Доказательство.Rp ( z)
f n ( z)
Ql ( z )
.
m ( z)
m ( z)
По условию:
m ( z ) ( z a );
По основному свойству деления:
Ql ( z ) Qn 1 ( z );
R p ( z ) R0 ( z ) R0 ;
f n ( z ) Qn 1 ( z ) ( z a) R0
Пложим z = a, тогда
f n ( a ) R0
13.
Следствие.Для того чтобы многочлен
( z a)
f n (z )
делился на
без остатка, необходимо и достаточно,
чтобы число z=a было его корнем .
Итак, если z = z0 - корень многочлена f n (z ),
f n ( z ) ( z z0 ) Qn 1 ( z )
Другие корни f n (z ) следует искать из уравнения
и т.д.
Qn 1 ( z ) 0
14.
ЕслиЕсли
где
где
f n ( z ) ( z z0 ) Qn k ( z ),
k
Qn k ( z0 ) 0,
то
то z0 называется
называется корнем
корнем кратности
кратности kk
многочлена
многочлена
f (z ).
n
15.
Основная теорема алгебрыТ Многочлен n-ой степени имеет ровно n
корней, если каждый корень считать столько
раз, какова его кратность.
Т1
Если коэффициенты уравнения n-ой степени
действительные числа и z x iy
0
0
0
корень этого уравнения, то сопряжённое число
z x0 iy0
*
0
- также корень этого уравнения.
16.
Таким образом:Комплексные корни многочлена с действительными
коэффициентами являются сопряженными парами
корней .
17.
Из теоремы Безу и основной теоремы алгебры следует,что всякий многочлен степени n можно разложить на
множители:
f n ( z ) a0 ( z z1 )
( z z2 ) ...( z zm )
k1
k2
km
18.
Здесьz1
z2
- корень кратности k1,
- корень кратности k2,
…………………………..
k1 k 2 ... k m n
Если коэффициенты f n (z ) - действительные
числа, то, объединяя скобки, соответствующие
комплексно-сопряжённым корням, можно
представить этот многочлен в виде произведения
множителей двух типов:
19.
1. Линейные множителиz zi
ki
- соответствуют действительным корням zi
кратности ki,
2. Квадратичные множители
z
2
pz q
kj
где p,q - действительные числа, D p 2 4q 0
- соответствуют парам комплексно-сопряжённых
корней кратности kj
20.
Для доказательства последнего рассмотрим:(z z j ) (z z )
*
j
z
x
iy
z
x
iy
j
j
j
j
Здесь:
z 2x j z x y
2
z pz q ;
2
2
p 2 x j ; q x j y j ;
2
2
j
2
j
D p 4q 4 x 4 x y 0
2
2
j
2
j
2
j
21.
Таким образом, многочлен с действительнымикоэффициентами имеет разложение:
f n z a0 z z1
s1
z z2
s2
... z zl
sl
kj
( z p1 z q1 ) ....( z p j z q j ) ,
2
k1
2
где
s1 s2 ... sl 2k1 ... 2k j n
22.
Пример:
Разложить на множители
f 4 z z 1.
4
Решение.
Действительных корней нет. Комплексные корни:
i
z 1 0i e ,
4
4
1 0i e
k 0;1; 2;3.
i 2 k
4
,
23.
z1 ei
4
z2 e
z3 e
z4 e
i 3
4
2
2
i
2
2
2
2
, 2 i 2
i 5
4
i 7
4
,
2
2
i
z 2*
2
2
2
2
i
z1*
2
2
24.
Парыz1, z4 ; z2, z3
сопряжённые
z 1 z z1 z z4 z z2 z z 3
4
z z z1 z4 z1 z4
2
z1 z4 1
z
2
z z2 z3 z2 z3 .
z1 z 4 2
25.
Точно также,z2 z3 1
z2 z3 2,
Окончательно
z 1 z 2z 1 z 2z 1 .
4
2
2



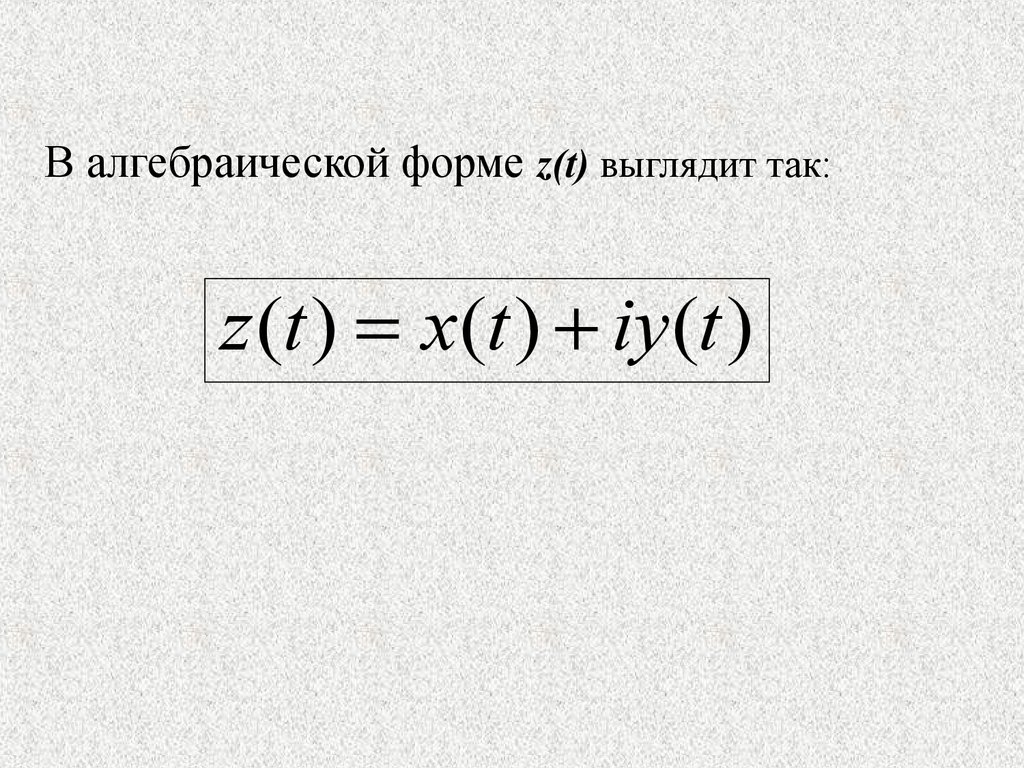


















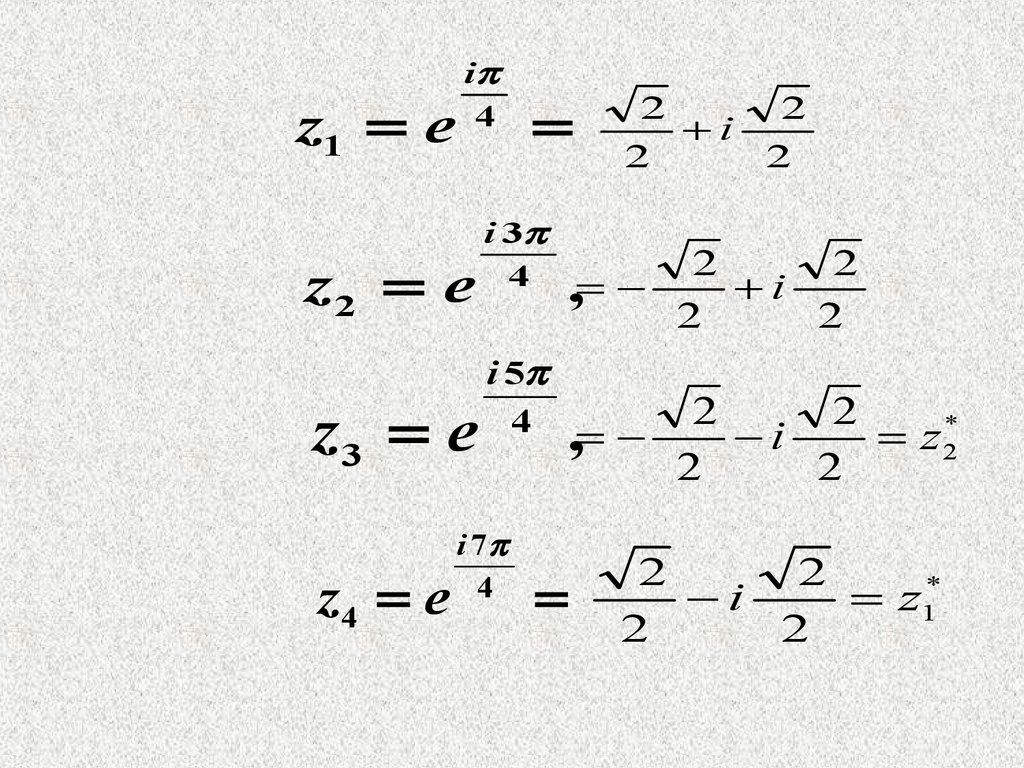
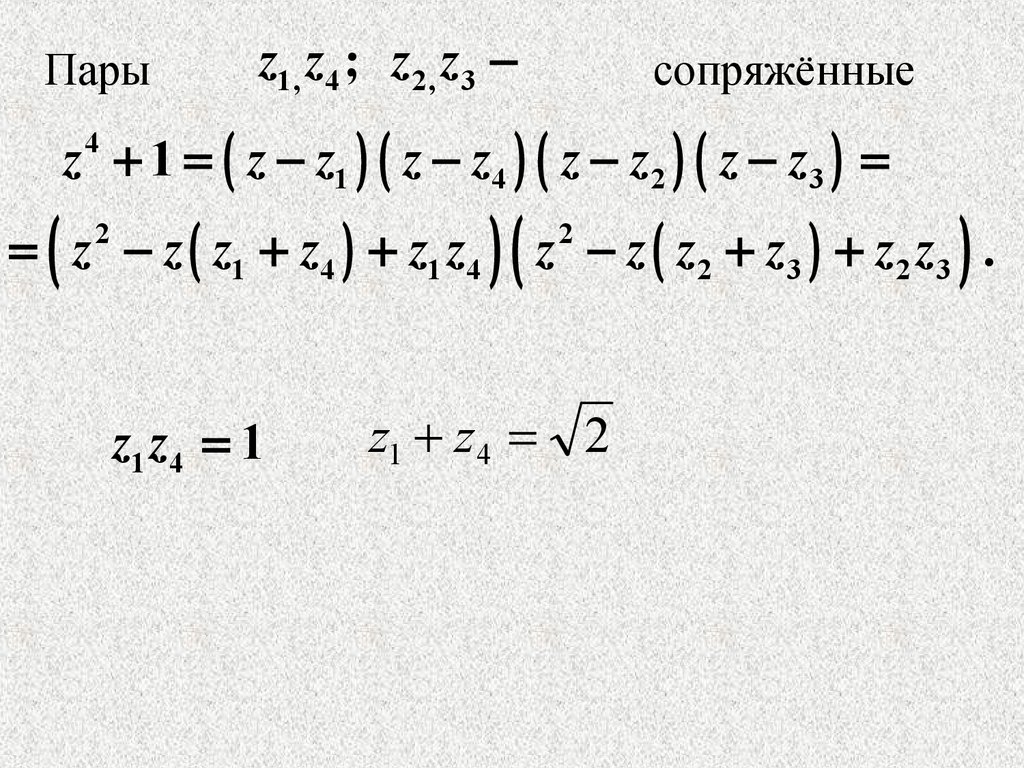

 mathematics
mathematics








