Similar presentations:
Лекции по теории функции комплексной переменной
1. Лекции по теории функции комплексной переменной
Уфимский государственный авиационныйтехнический университет
Общенаучный факультет
Кафедра математики
Лекции по теории функции
комплексной переменной
Уфа 2016г.
2.
Лекция № 1§1. Комплексные числа и
последовательности комплексных
чисел.
п. 1. Понятие комплексного числа.
Геометрическая интерпретация.
3.
Рассмотрим плоскостьR2.
z x , y R
2
2
2 -вектор
x R, y R. Определим z
x y , 1
операцию сложения:
z1 x1 , y1 , z2 x2 , y2 z( x , y ) :
x x1 x2
z z1 z2
; 2
y y1 y2
i
y
0
z x, y
z
i z z1 z2
1
z2
x
1
0
1
4.
операцию умножения на число:z x , y , R :
1 1, 0
z x , y
i 0, 1
базис
z x , y x 1 y i
Как ввести z z1 z2 ,
3
5.
Вектор 1– единица операции умножения.Определим i i i 2 . Т.к. 1 i i , то полагают
i 1. 4
1,0
i
i
2
1,0
2
0
2
2
iz
z
1
1,0
0
z ( x , y ) : z i ( x 1 y i ) i y 1 x i y, x
5
6.
z1 x1 , y1 , z2 x2 , y2 Rz1 z2 ( x1 , y1 ) ( x1 , y1 )
Правило умножения
2
( x1 1 y1 i ) ( x2 1 y2 i )
x1 x2 y1 y2 1 x1 y2 x2 y1 i
x1 x2 y1 y2 ; x1 y2 x2 y1 6
2
Def. Числовая плоскость R называется
комплексной плоскостью C, если для ее точек
определены модули (1), операции сложения (2)
и умножения (6).
Точки комплексной плоскости С называются
комплексными числами.
7.
Действительные числа включаются вмножество комплексных чисел.
a=(a,0)-вещественное число, 0=(0, 0), 1=(1, 0),
-1=(-1, 0), ib= (0, b)-чисто мнимое число,
i =(0, 1)- мнимая единица, -i=(0, -1).
Равенство. z1 x1 , y1 , z2 x2 , y2 :
x
x
1
2
z1 z2
.
y1 y2
Алгебраическая форма записи.
z x i y Re z i Im z .
упорядоченная
пара
z ( x , y )
вещественных чисел.
8.
Комплексное сопряжение.*
*
*
z z x i y ( x , y ). Re z x , Im z y .
*
*
z z Im z z z , * *
Re z
z1 z2
2
*
*
,
* *
z1 z2 ,
z z,
2i
z1 z2
*
2
* *
z1 z2 ,
2
2
z z ( x iy )( x iy ) x y z
Деление.
*
* x x y y
z1 z1 z2 z1 z2
1 2
1 2 i y1 x2 y2 x1
2
2
2
2
z2 z2 z*2 z 2
x 2 y2
x 2 y2
2
9.
Примеры.2
2
z x iy x y i 2 xy ;
1, n 4k
i
n 4k 1
n
*
i
, k 0,1,2...; i i;
1 n 4k 2
i n 4k 3
2
2
3 4i 3 4i 2 3i 6 12
8 9
i
2 3i 2 3i 2 3i 22 32 22 32
6 17
1
i
i ;
i
13 13
10.
Z-2+2i
Re z=0
Комплексные числа можно изображать точками
на комплексной плоскости.
Y (Im z)
2
2+2i
1
i
X (Re z)
0
-2
-1
0
-1
-2-2i
-2
1
-i
2
Im z=0
2-2i
11.
Модуль и аргумент комплексного числаIm z
z=x+iy
Z
iy
Arg z arg z 2 k
0
r
j
j
r
z
Re z
x
-iy
z*=x-iy
12.
Полярные координаты (x,y) (r,j).x r cos j
y r sin j
Модуль комплексного числа:
2
2
r x y z
Re z Im z
2
2
Аргумент комплексного числа:
y Im z
tg j
; j j 0 2 k ; 0 j 0 0 2
x Re z
Arg z arg z 2 k ;
0 arg z 0 2 Главное значение аргумента.
13.
arg z0 arg z 2
-разрез по Re z 0
-разрез по Re z 0
Примеры. 0 0, arg 0 — не определен!
i 1, arg i ;
2
1 1, arg 1 ; i 1, arg i ;
2
z 2 2i , z 2 2 , arg z ;
4
1 1, arg1 0;
14.
Тригонометрическая форма записиz x i y , x r cos j , y r sin j .
z r cosj i sinj , r z , j Arg z .
формула Эйлера: j e
ij
cosj i sinj , j R.
Показательная форма записи
ij
z re
, r z , j Arg z .
Теорема.1.1. Пусть j , R, k Z , тогда
i0
ij i
i j
1) e
3) e
i j 2 k
1; 2) e e
ij
e ; 4) e
ij
e
1
ij
;
; 5) e
ij
1.
15.
Примеры.i0
1 1 cos 0 i sin 0 e ;
i
i 1 cos i sin e 2 ;
2
2
i
1 1 cos i sin e ;
i
3 i 2e 6 ;
3
i
2 2i 2 2e 4 ;
2
i
i 3 1 2e 3 ;
i
i 1 cos i sin e 2 ;
2
2
3
i
i
i
i
i 4
i 4
4
e e e e e e 4 .
16.
Вопрос.j
j
i 2
ij
2 12 1 j ?
e e
Умножение и деление в показательной форме.
ij1
ij 2
z1 r1e , z2 r2e ,
z1 r1 i j1 j 2
i j1 j 2
e
.
z1z2 r1r2e
,
z2 r2
ij
Формула Муавра. z re r cosj i sinj .
n
n
n inj
n
z r e
r cosj i sinj
n
r cos nj i sin nj .
cosj i sinj cos nj i sin nj
n
17.
Извлечение корня. z reij
r cosj i sinj
r cos j 2 k i sin j 2 k re
i j 2 k
;
j 2 k
i
n z n re n ,
n z n r cos j 2 k i sin j 2 k ,
n
n
k 0, 1 , n 1.
Корень n-той степени из комплексного числа
принимает n различных значений.
18.
Примеры.1 i
3
3 i
2 e 4
3
9
i
3
i
3
3
4
2 e
2 e 4
3 2
2 cos i sin
4
4
3
2
2
i 2 2i .
2
2
19.
3 2 2i1
i 2
1 / 3 3 4
8 e
k
i
e 12 , k 0;
7
i
2
e 12 , k 1;
3
i 5
i
e 4 e 4 1 i , k 2;
20.
i0e 1, k 0;
i
2 k
i
2
e
i , k 1;
4 1 e 4
i
e 1, k 2;
i 3
i
e 2 e 2 i , k 3.
21.
ie 4 2 1 i , k 0;
2
i 3
2 k e 4 2 1 i , k 1;
i
4 1 e
2
4
3
i
2
4
1 i , k 2;
e
2
i
2
4
e
1 i , k 3.
2
22.
Множество комплексных чисел C образует поле.Поле С не является упорядоченным.
В упорядоченном поле P
a ,b P
a 0 В поле С 12 i 2 0, но
a b 0
.
b 0
1 0, i 0.
2
2
Операция сравнения в С не определена.
Утверждение 1 i i 1 0 неверно.
Модуль
2
z x y
аксиомам норм.
2
удовлетворяет
23.
Неравенства треугольника.z1 z2 z1 z2 z1 z2
Упорядоченная четверка E C , , ,
является нормированным векторным
пространством над полем R. Оно превратится в
метрическое пространство, если z1 , z2 C
ввести метрику по формуле z1 , z2 z1 z2 .
24.
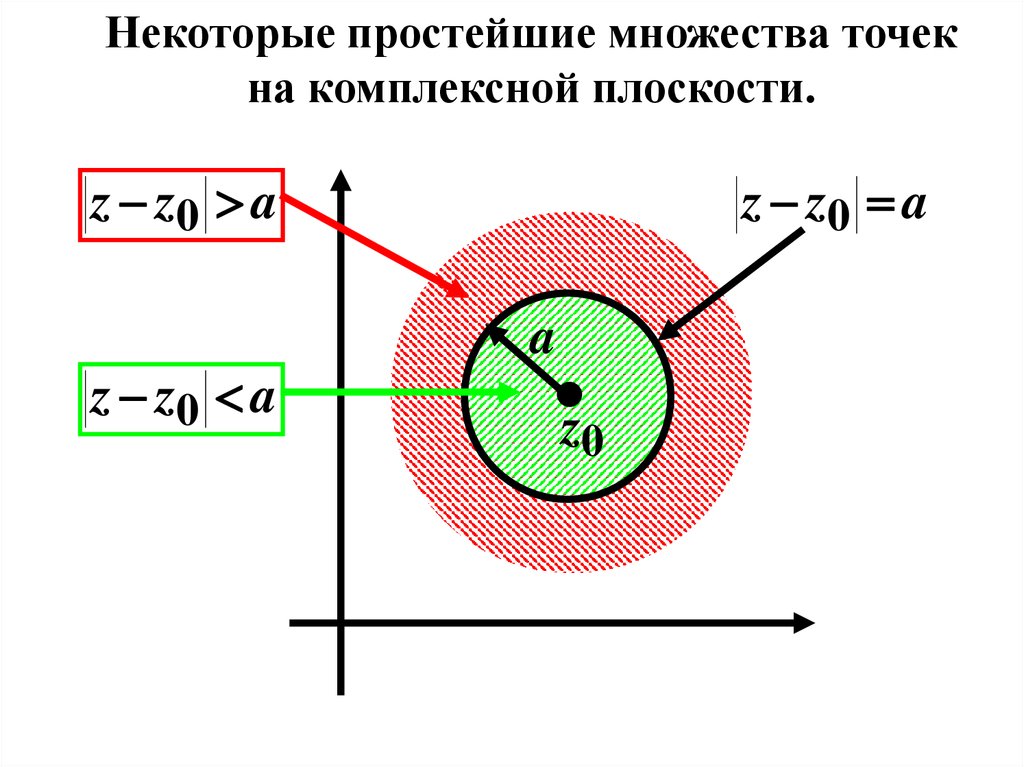
Некоторые простейшие множества точекна комплексной плоскости.
z z0 a
z z0 a
z z0 a
a
z0
25.
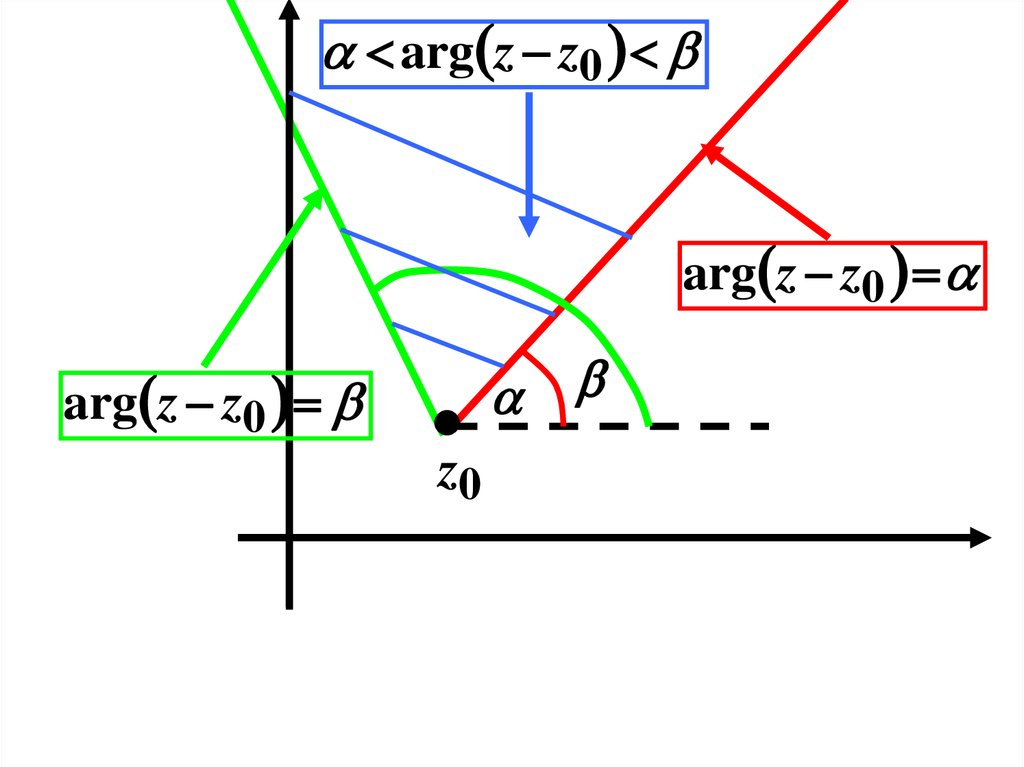
arg z z0arg z z0
arg z z0
z0
26.
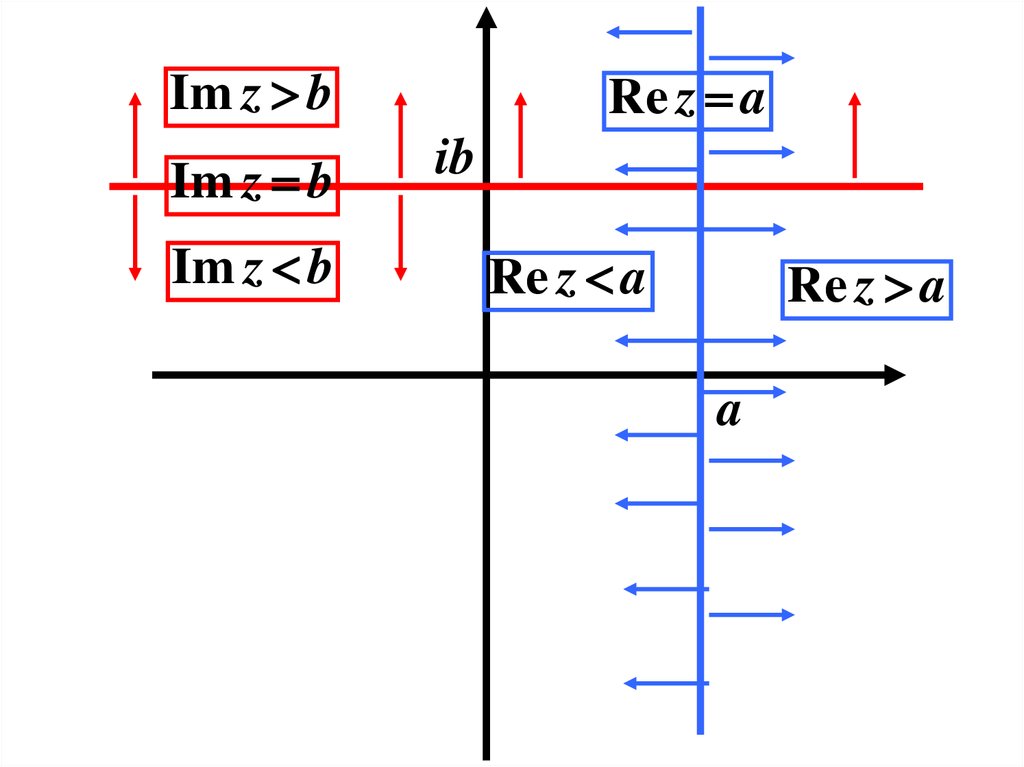
Im z bIm z b
Im z b
Re z a
ib
Re z a
Re z a
a
27. п.2. Последовательности комплексных чисел.
Def. Последовательностью комплексных чиселназывают упорядоченное счетное множество
Обозначение: zn
комплексных чисел.
Члены последовательности располагаются в
порядке следования их номеров.
Сходящиеся последовательности.
Def. Комплексное число z называется пределом
последовательности zn , если для 0
N : z zn , n N .
z z , lim zn z .
n
n
28.
Примеры.n
z
z
lim 1 e ;
n
n
n
не
1
0, n 2k
lim arg
lim
существует
n
n
n , n 2k 1
Каждый член последовательности
zn an ibn zn an i bn .
Т.1.2. Необходимым и достаточным условием
сходимости zn z a ib является
требование an a , bn b.
29.
Def. Последовательность zn называетсяограниченной, если A 0 : zn A n.
Сходящаяся последовательность ограничена.
Т.1.3. Из всякой ограниченной
последовательности можно выделить
сходящуюся подпоследовательность.
Критерий Коши. Необходимым и достаточным
условием сходимости zn z является
требование, чтобы для 0 N :
zn m zn , n N , m 0.
30. Неограниченно возрастающие последовательности.
Def. Если для A 0 N A : zn A, n N ,то последовательность zn называется
неограниченно возрастающей.
n
Примеры. zn z , z 1;
zn in.
! z : lim zn . z 0; z ;
0
n
z
;
z
;
1
zn n 0.
0
;
zn
;
0
31.
Все неограниченно возрастающиепоследовательности сходятся к единственной
бесконечно удаленной точке комплексной
плоскости.
Def. Комплексная плоскость дополненная
бесконечно удаленной точкой называется
расширенной комплексной плоскостью.
Def. Окрестностью бесконечно удаленной точки
называется множество z : z R внешность
круга с центром в начале координат достаточно
большого радиуса R.
32.
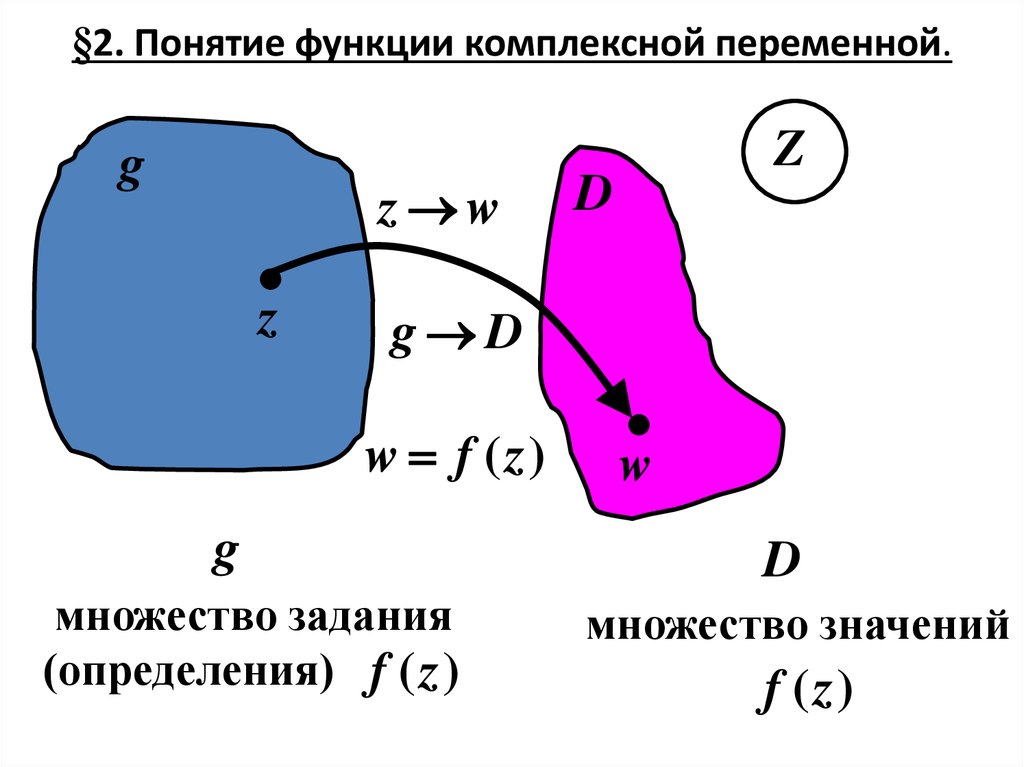
33. §2. Понятие функции комплексной переменной.
gz w
z
Z
D
g D
w f (z )
g
множество задания
(определения) f (z )
w
D
множество значений
f (z )
34. Точки множества.
Def. Точка z0 g называется внутреннейточкой множества g , если
z0 z : z z0 : z0 g .
Def. Множество, состоящее из внутренних
точек называется открытым множеством.
g
z0
z0
35.
Def. Множество g называется связным, еслиz1 , z2 g можно соединить кусочно-гладкой
кривой L g .
Def. Область— открытое, связное множество.
Def. Точка z0 g называется граничной
точкой множества g , если в z0
z1 g и z2 g .
Def. Совокупность граничных точек множества
g называется границей множества g.
g , C , , ,
36.
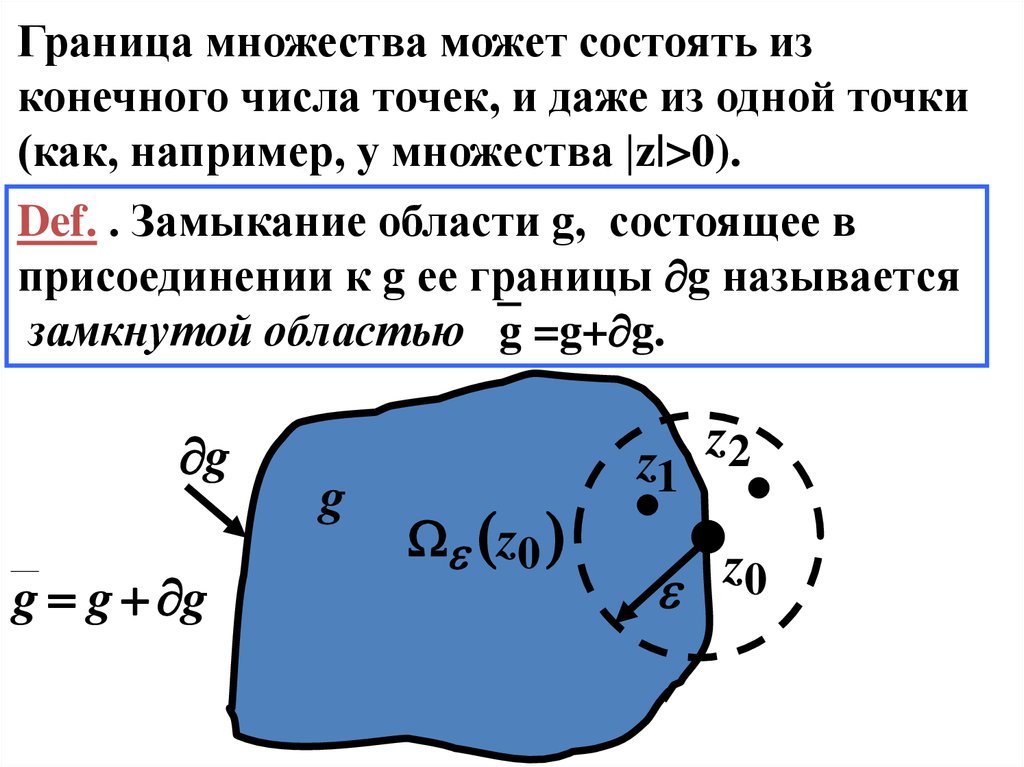
Граница множества может состоять изконечного числа точек, и даже из одной точки
(как, например, у множества |z|>0).
Def. . Замыкание области g, состоящее в
присоединении к g ее границы g называется
замкнутой областью g =g+ g.
g
g g g
g
z0
z
z1 2
z0
37.
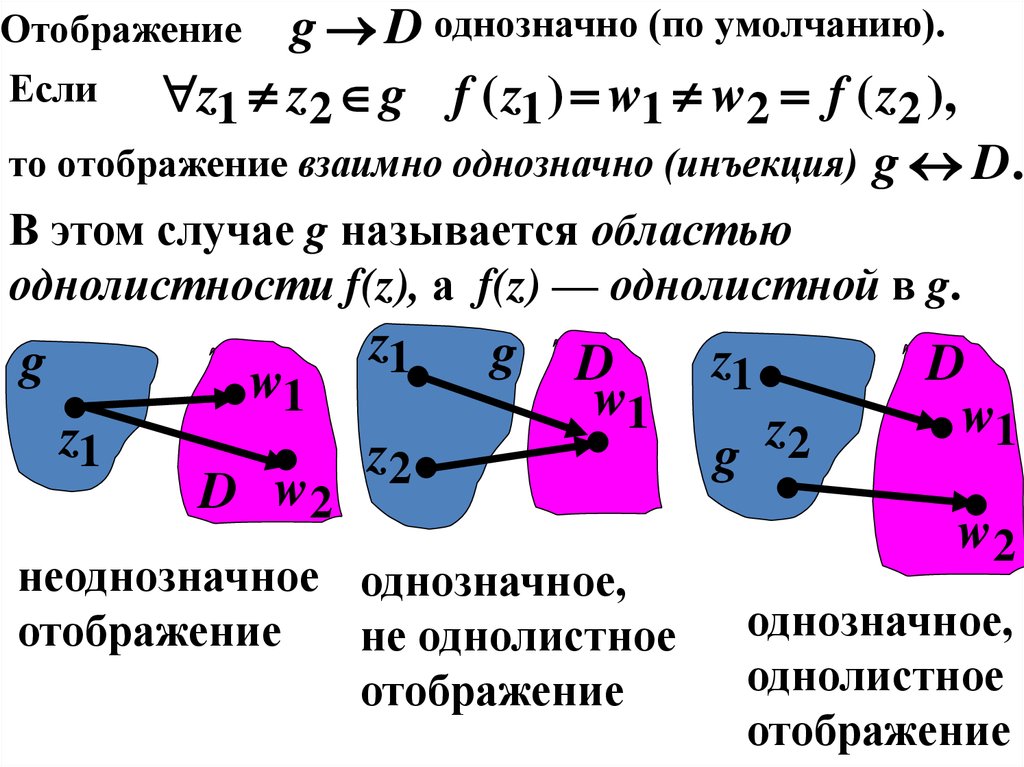
g D однозначно (по умолчанию).Если
z1 z2 g f ( z1 ) w1 w2 f ( z2 ),
то отображение взаимно однозначно (инъекция) g D.
Отображение
В этом случае g называется областью
однолистности f(z), а f(z) — однолистной в g.
g
z1
w1
D w2
z1
z2
g
D
w1
неоднозначное однозначное,
отображение
не однолистное
отображение
z1
g
z2
D
w1
w2
однозначное,
однолистное
отображение
38.
При g D когда область значений совпадает с Dв D обратная функция z=j(w),
осуществляющая отображение D g.
Если отображение g D однозначно, но не
однолистно, то можно говорить об обратной
функции, но она не будет однозначной.
При z=x+iy, w= f(z)=u(x,y)+iv(x,y).
Свойства функции комплексной переменной
определяются свойствами функций двух
действительных переменных.
39. Некоторые элементарные функции комплексной переменной.
1. w f ( z ) az b;z x iy , a a1 ia2 ke
i
, b b1 ib2 .
Однозначная, однолистная на всей комплексной
плоскости.
Геометрический смысл: растяжение в k раз,
поворот на угол , параллельный перенос
вдоль вектора b.
Единственное отображение, сохраняющее
подобие всех фигур.
40.
2. w f ( z ) z 2 x 2 y 2 i 2 xy , z x iy .2 2ij
ij
w f (z) r e
, z re
.
Однозначная, но не однолистная на всей
комплексной плоскости. f ( z ) w1 w2 f ( z );
Область однолистности— полуплоскость
C arg z C , C R.
Область однолистности отображается на всю
комплексную плоскость.
Любая прямая, не проходящая через точку
z=0 отображается в параболу. Декартова сеть
линий в верхней полуплоскости отображается
в 2 взаимно ортогональных семейства
софокусных парабол.
41. Декартова сеть
4.4
3
Im ( Zh)
Im ( Zv)
2
Im ( Zb)
1
0
0
2
2.
1
0
Re ( Zh) Re ( Zv) Re ( Zb)
1
2
2
42.
Отображение декартовой сети в Im z 02
w z
2
2
1
Im ( Wh)
Im ( Wv)
0
Im ( Wb)
1
2
2
2
2
1.5
1
0.5
0
0.5
Re ( Wh) Re ( Wv) Re ( Wb)
1
1.5
2
2
43.
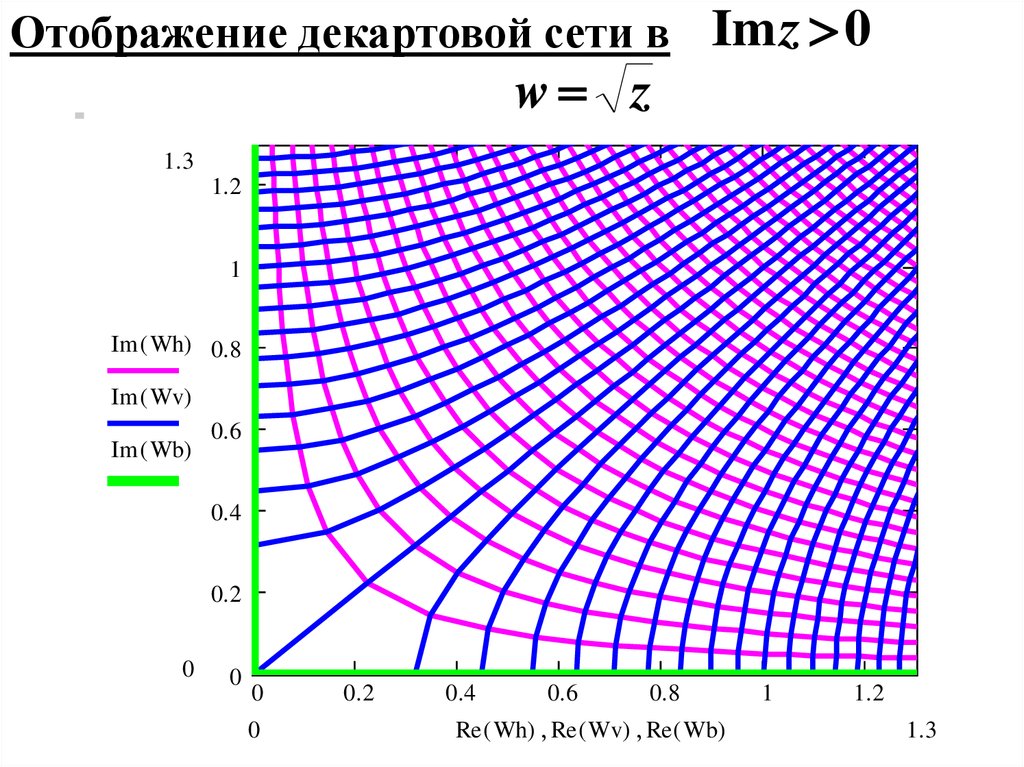
3.w f (z) z.
Многозначная функция.
Две ветви: w1 z , w2 z .
Точки ветвления, при обходе которых по
любому замкнутому контуру происходит
переход с одной ветви на другую z 0, z .
На плоскости с разрезом по отрицательной
части вещественной оси arg z
каждая ветвь— однозначная функция.
w1 z главное значение. arg w1 .
2
2
w1 z
arg z Re w1 0 .
44.
Отображение декартовой сети в Im z 0w z
1.3
1.2
1
Im ( Wh) 0.8
Im ( Wv)
Im ( Wb)
0.6
0.4
0.2
0
0
0
0
0.2
0.4
0.6
0.8
Re ( Wh) Re ( Wv) Re ( Wb)
1
1.2
1.3
45.
4. w f ( z ) 1z
x
2
x y
2
i
y
2
x y
2
, z x iy .
1 ij
ij
w f (z) e
, z re .
r
Однозначная, однолистная на всей комплексной
плоскости.
Геометрический смысл: симметричное
отражение относительно вещественной оси и
инверсия относительно единичной окружности.
46.
Отображение декартовой сети в10
1
w
z
z
10
Im ( Wh)
Im ( Wv)
0
Im ( Wb)
10 10
10
10
5
0
Re ( Wh) Re ( Wv) Re ( Wb)
5
10
10



















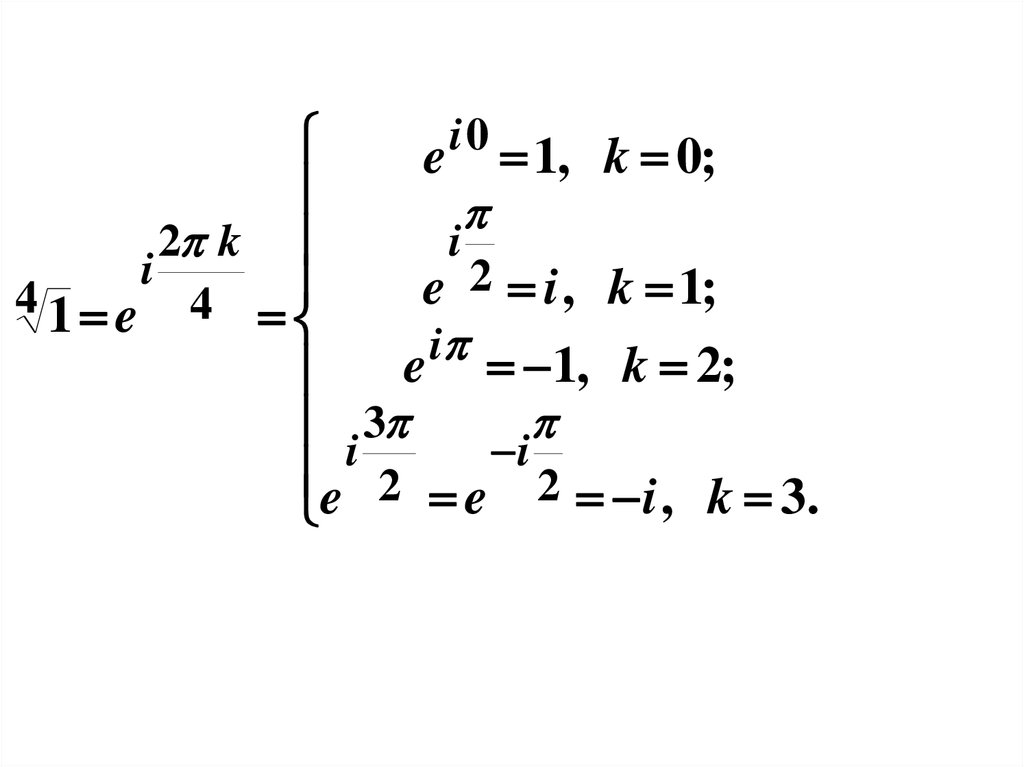



















 mathematics
mathematics








