Similar presentations:
Элементы теории функций комплексного переменного (пр.2)
1.
ТомскийТомский политехнический
политехнический университет
университет
Доцент, к.ф.м.н.
Богданов Олег Викторович
Элементы теории функций комплексного
переменного (Пр.2)
2.
Комплексные числаПонятие комплексного числа.
В множестве действительных чисел действие извлечения
корня четной степени из отрицательного числа невыполнимо.
Выражения
1, 9 , 4 7 не имеют смысла и, поэтому, уравнения
x 2 1 = 0, x 4 16 = 0, x 2 6 x 25 = 0
на этом множестве решений не имеют.
Для того, чтобы сделать возможным извлечение корня четной степени
из отрицательного числа множество действительных чисел было
расширено добавлением к нему множества мнимых чисел.
1,
О п р е д е л е н и е 1. Число, квадрат которого равен
называется мнимой единицей и обозначается буквой
i2 = 1 .
i.
3.
Итак, используя мнимую единицу, можно записать корни квадратных уравнений:x 2 1 = 0,
x 2 1, x1, 2 1 i
x 2 4 = 0, x 2 4, x1, 2 4 4
( 1) 2 1 2i
x 2 6 x 25 = 0, x1, 2 3 9 25 3 16
3 16
( 1) 3 4 1 3 4i
1 1 8 1 7
x 2 x 2 = 0, x1, 2
2
2
1 7
( 1) 1 7
i
1
7
i
2
2
2 2
4.
О п р е д е л е н и е 2. Число видаx, y
действительные числа, а
z = x i y, где
i мнимая единица,
называется комплексным числом.
Число
x
называется действительной частью комплексного числа
и обозначается
Число
y
x = Re z = Re( x i y)
называется мнимой частью числа и обозначается
y = Im z = Im( x i y)
Запись комплексного числа в виде
z = x i y,
называется алгебраической формой записи
комплексного числа.
Число
, не содержащее действительной части,
z = iy
называется чисто мнимым числом.
О п р е д е л е н и е 3. Комплексное число, имеющее ту же действительную
и противоположную по знаку мнимую часть, называется
z = x i y и обозначается
комплексно-сопряженным с числом
z = x i y = x i y.
5.
О п р е д е л е н и е 4. Числоz = x iy
и обозначается
x2 y 2
| z |, или
называется модулем числа
r:
| z |= r = x 2 y 2 .
Очевидно, что
| z | 0
Действия над комплексными числами в алгебраической форме
1. Условие равенства комплексных чисел: два комплексных числа
z1 = x1 i y1
и
z2 = x2 i y2
равны тогда и только тогда, когда равны их действительные и мнимые
z1 = z1
x1 = x2 , y1 = y2 .
6.
2. Сложение и вычитание комплексных чисел:при сложении и вычитании комплексных чисел складываются и
вычитаются их действительные и мнимые части
(2 3i ) (1 4i ) = (2 1) i ( 3 4) = 3 i,
(3 5i ) (2 4i ) = (3 2) i ( 5 4) = 1 9i,
(1 4i ) ( 3
2
i ) (1
3) i
(4
2 ).
3. Умножение комплексных чисел на постоянное число:
при умножении комплексных чисел на постоянное число нужно умножить
на это число его действительную и мнимую части
2 (3 i ) 6 2i,
5 (4 2i ) = 20 10i,
i (1 2i ) = i 2i 2 = i 2 , так как
i2 = 1 .
Можно совместить два действия
2 (3 i ) 5 (4 2i ) = 6 2i 20 10i = 26 8i,
4 (2 i ) i (1 2i ) = 8 4i i 2i 2 = 8 5i 2 = 10 5i.
7.
4. Умножение комплексных чисел :при умножении двух комплексных чисел нужно умножить их как обычные
многочлены, учесть, что
i 2 = и1 привести подобные
(2 3i )(1 4i ) = 2 8i 3i 12i 2 = 2 5i 12 = 14 5i,
(3 5i )(2 4i ) = 6 12i 10i 20i 2 = 6 2i 20 = 26 2i,
(4 3i ) 2 = 16 24i 9i 2 = 16 24i 9 = 7 24i
Найдем произведение двух комплексно-сопряженных чисел
z
z = ( x iy )( x iy ) = x 2 ixy ixy i 2 y 2 = x 2 y 2 .
Итак, произведение
z
z = x 2 y 2 =| z |2 .
есть действительное число, равное сумме квадратов действительной и
мнимой части комплексного числа. Или: произведение двух
комплексно-сопряженных чисел равно квадрату модуля комплексного числа
(3 2i )
(3 2i ) = 32 22 = 13.
(1 i )
(1 i ) = 12 12 = 2.
( 3
2i )
( 3
2i ) = ( 3 )2 ( 2 )2 = 3 2 = 5.
8.
З а м е ч а н и е.Используя результат произведениякомплексно- сопряженных чисел, можно проводить разложение
на множители суммы квадратов действительных чисел
x 2 y 2 = ( x iy )( x iy ).
x 2 25 = ( x 5i )
( x 5i ).
x 2 4 x 5 = x 2 4 x 4 1 = ( x 2)2 1 = ( x 2 i )( x 2 i ).
5. Деление комплексных чисел :
при делении двух комплексных чисел нужно умножить числитель и знаменатель
дроби на сопряженное знаменателю выражение, провести умножение в
числителе и упростить с учетом, что в знаменателе будет произведение
сопряженных чисел, т.е. действительное число
2 3i (2 3i )(1 4i ) 2 3i 8i 12i 2
(2 3i ) : (1 4i ) =
=
=
=
1 4i (1 4i )(1 4i )
1 16
10 11i
10 11
=
=
i.
1 16
17 17
(4 5i ) : i =
4 5i (4 5i )( i )
=
=| i 2 = 1 |= 4i 5i 2 = 5 4i.
i
i ( i )
1 1
( i ) i
=
=
= i
i i
( i) 1
1
= i.
i
9.
Построение комплексных чисел на плоскостиВ декартовой системе координат на плоскости на оси OX откладывается
действительная часть комплексного числа, и ось OX называется
действительной осью, а на оси OY откладывается мнимая часть комплексного
числа, и ось OY называется мнимой осью комплексной плоскости XOY.
Тогда комплексное число изображается точкой на плоскости с координатами
x
и
y,
а также радиус-вектором этой точки
OM = {x, y}.
Длина радиуса-вектора точки есть модуль комплексного числа
| z |=| OM |= x 2 y 2 .
10.
Тригонометрическая форма записи комплексного числаПоложение точки
z = x iy
комплексной плоскости определяется
не только декартовыми
( x , y ),
но и полярными координатами
(r , )
расстояние от точки до
где
начала координат, т.е. длина
или модуль радиус-вектора,
r
угол между положительным направлением действительной оси
и радиусом-вектором.
Этот угол называется
аргументом
комплексного числа и определяется с точностью до
Множество всех значений угла обозначается
Arg z
При работе с комплексными числами обычно используется так
называемое главное значение аргумента
= a, rg z
arg z
,
Arg z = arg z 2
k.
которое удовлетворяет условию
Таким образом,
2
k , k = 1,2,3,...
11.
Из рисунка видно, чтоx = r cos
, y = r sin
,
z x iy r cos i
r sin
и любое комплексное число
можно представить в виде
z = r (cos i sin ).
Подобная запись называется
записи
тригонометрической формой
комплексного числа.
Число, комплексно-сопряженное к данному, запишется в виде
z = r (cos i sin ).
Любое число можно перевести из тригонометрической формы записи
в алгебраическую и обратно. Кроме того, из тригонометрической формы
записи можно получить еще показательную форму записи комплексног
12.
Принято определять аргумент числа в зависимости от знаковдействительной и мнимой частей числа следующим образом:
arctg
= arg z = arctg
arctg
y
x
x > 0, (I, IV ),
y
x < 0, y 0, ( II),
x
y
x < 0, y 0, ( III)
x
Приведем значения арктангенсов некоторых углов
arctg 0 = 0,
arctg = /2,
arctg (
) = /2.
arctg (1/ 3 ) = /6, arctg ( 1/ 3 ) = /6,
arctg 1 = /4,
arctg ( 1) = /4,
arctg ( 3 ) = /3,
arctg ( 3 ) = /3.
13.
Зачастую в расчетах далеко не всегда участвуют основные острые углытангенсы которых известны. В случае произвольного угла используем
калькулятор, который с некоторой степенью точности даст значение уг
в радианах или в градусах:
arctg (2,835) 1.23 70,6o ,
arctg (67,83) 1.56 89,2o ,
arctg ( 0,324) 0,31 18o.
Для правильного определения аргумента следует всегда изобразить
число на комплексной плоскости для того, чтобы определить, в какой
четверти находится данное число. .
Рассмотрим примеры нахождения аргумента комплексных чисел.
14.
z 4, arg (4) = arg (4 0i ) = arctg (0/4) = arctg 0 = 0,
z 4, arg ( 4) = arg ( 4 0
i ) = arctg (0/( 4)) = arctg 0 =
,
z 3i, arg (3i ) = arg (0 3i ) = arctg (3/0) = arctg =
/2,
z 3i, arg ( 3i ) = arg (0 3i ) = arctg ( 3/0) = arctg ( ) =
/2,
z 1 i, arg (1 i ) = arctg (1/1) = arctg 1 =
/4
z 1 i, arg (1 i ) = arctg ( 1/1) = arctg ( 1) =
/4,
z 1 i, arg ( 1 i ) = arctg (1/( 1)) = arctg ( 1) =
/4 = 3
/4,
z 1 i, arg ( 1 i ) = arctg ( 1/( 1)) = arctg 1 =
/4 = 3
/4.
15.
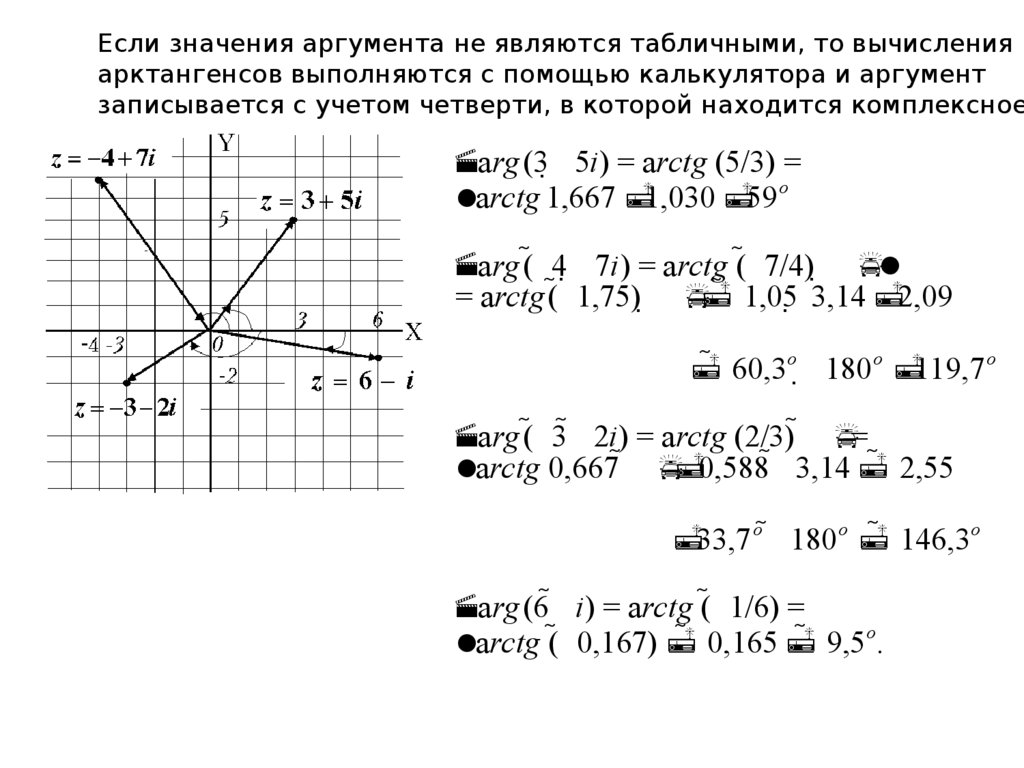
Если значения аргумента не являются табличными, то вычисленияарктангенсов выполняются с помощью калькулятора и аргумент
записывается с учетом четверти, в которой находится комплексное
arg (3 5i ) = arctg (5/3) =
arctg 1,667 1,030 59 o
arg ( 4 7i ) = arctg ( 7/4)
= arctg ( 1,75) 1,05 3,14 2,09
60,3o 180 o 119,7 o
arg ( 3 2i ) = arctg (2/3) =
arctg 0,667 0,588 3,14 2,55
33,7 o 180 o 146,3o
arg (6 i ) = arctg ( 1/6) =
arctg ( 0,167) 0,165 9,5o.
16.
Комплексное число в показательной формеПусть комплексное число записано в тригонометрической форме
z = r (cos i sin ).
Воспользуемся формулой Эйлера
cos i sin = ei .
Тогда получим
Выражение
z = r (cos i sin ) = rei .
z = re
i
- показательная форма записи числа .
Отметим, что комплексно-сопряженное число в показательной
форме будет иметь вид
z = re
i
.
Показательная и тригонометрическая формы записи комплексного числа
применяется для выполнения операций умножения, деления комплексных
чисел, а также для возведения в целую положительную степень и
извлечения корня.
17.
Действия над комплексными числами в показательной итригонометрической формах
Пусть
z1 = r1e
i
1
z1 z2 = r1 e
, z2 = r2 e
i
1
r2 e
i
1
i 2
z1: z2 = r1 e : r2 e
i 2
= r1 r2
i ( 1 2 )
e
.
r1 i ( 1
= e
r2
i 2
2 )
.
a) При умножении комплексных чисел их модули перемножаются,
а аргументы складываются.
b) При делении комплексных чисел их модули делятся, а аргументы выч
3e3 i/4
2e2 i/3 = 6ei (3 /4
5e
4e i/4
i/3
2 /3)
= 20ei ( /4
3e3 i/4 3 i (3 /4
2 i/3 = e
2
2e
2 /3)
/3)
3 i/12
= e
,
2
= 6 e(17 /12) i ,
= 20 e
i/12
,
18.
Отметим ряд интересных результатовЧисло
i
имеет модуль равный единице, и аргумент
i
Поэтому, при умножении на число
к аргументу прибавится
изображающего число
,
2
z,
,
2
некоторого числа
т.е.
i = ei /2 .
z = r ei
что приведет к повороту вектора,
на
90 o
в положительном направлении
без изменения длины.
Перевод числа из одной формы записи в другую
1.
От алгебраической к тригонометрической и показатель
Для перехода к тригонометрической и показательной форме
представления комплексного числа находим:
1) модуль числа по формуле
2) аргумент числа
= arg z
r =| z |= x 2 y 2 ,
19.
z = x iy z r (cos), z r
ei
i sin
1. z = 1 i =
r =| z |= 1 1 = 2
/4
= arg z = arctg1 =
i
z = 1 i = 2e 4 ,
z = 1 i = 2
cos i sin
4
4
2. z = 1 i 3 =
r =| z |= 1 3 = 2
= arg z = arctg (
i
3) =
/3
z = 1 i 3 = 2e 3 .
z = 1 i 3 = 2
cos i sin
3
3
20.
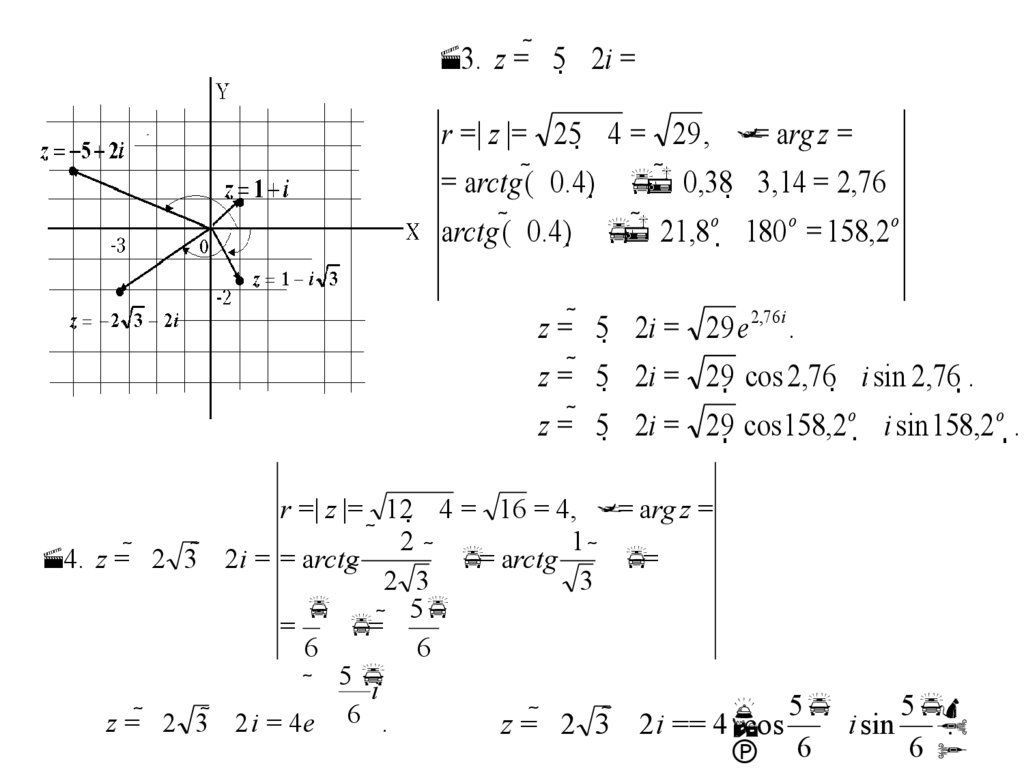
3. z = 5 2i =r =| z |= 25 4 = 29 , = arg z =
= arctg ( 0.4) 0,38 3,14 = 2,76
arctg ( 0.4) 21,8o 180 o = 158,2 o
z = 5 2i = 29 e 2,76 i .
z = 5 2i = 29 cos 2,76 i sin 2,76 .
z = 5 2i = 29 cos 158,2 o i sin 158,2 o .
r =| z |= 12 4 = 16 = 4, = arg z =
2
1
4. z = 2 3 2 i = = arctg
= arctg
=
2 3
3
5
= =
6
6
5
i
5
5
z = 2 3 2 i = 4e 6 .
z = 2 3 2 i == 4
cos i sin
.
6
6
21.
z = 4, | z |= 4, arg (4) = 0 z = 4 e0 i = 4 (cos 0 i sin 0).z = 4, | z |= 4, arg ( 4) = z = 4 e i = 4 (cos i sin ).
/2 i
z = 3i, | z |= 3, arg (3i ) = z = 3 e =3
cos i sin
.
2
2
2
z = 3i, | z |= 3, arg ( 3i )=
z=3 e /2 i =3
cos i sin
.
2
2
2
22.
2.От показательной к алгебраической
Пусть комплексное число задано в показательной форме
z = r ei
Для перехода к алгебраической форме:
1) сначала переходим к тригонометрическому представлению числа
i
z = r e = r (cos i sin ) = r cos i r sin .
2) Вычисляем
cos , sin
.
3) Находим действительную
x = rcos и мнимую
y = r sin
части числа и записываем окончательно число в алгебраической форме
z = x iy
23.
iz = e 2
= cos 2
i sin 2 = 1 i
0 = 1.
i
z = e
= cos
i sin = 1 i
0 = 1.
i
z = 2e
= 2[cos
i sin
] = 2( 1 i
0) = 2.
i
z = e 2 = [cos
2
2
i
z = e 2
= [cos
i sin
2
] = (0 i ) = i.
i sin
2
] = (0 1
i ) = i.
2
i
2
2
1
3
3
3 3
) i sin (
)] = 3(
)=
.
z=3e 3 =3[cos(
i
i
3
3
2
2
2
2
2,015i
= 7[cos( 2,015) i sin ( 2,015)]
z = 7e
7( 0,43 0,90 i ) = 3,01 6,32i.
24.
Возведение в степень и извлечение корняПоказательная и тригонометрическая форма записи комплексных чисел
Удобна для выполнения действий возведения в большую степень
и извлечения корня
n
z = re
n
n
i ( 2 k ) n
z = r ei ( 2 k )
n
=r e
i ( n 2 nk )
n
=r e
i n
.
2 k
i
n
n
n
= re
, (k = 0, 1, ..., n 1).
Соответствующие формулы в тригонометрической форме называются
формулами Муавра
z n = r n (cos n i sin n ).
n
2 k
2 k
i sin
z = n r
cos
, (k = 0, 1, ..., n 1).
n
n
25.
Задача. Выполнить действия с комплексными числами втригонометрической и показательной формах.
1. ( 2 3 2
i)6 .
Перейдем к показательной форме записи. Изобразим число
на комплексной плоскости. Оно находится в 3-ей четверти.
1) Находим модуль числа
| 2 3 2i |= 4
3 4 = 16 4.
2) Находим аргумент
2
=
arg ( 2 3 2i) = arctg
2 3
1
5
arctg
= =
.
6
6
3
3) Записываем число
4) Возводим в степень
z = 4 e
5
i/6
=4 e
z = 4e
=2 e
=
= 412 (cos( 5
) i sin( 5
)) = 412 cos( 5
) = 412.
6
5
i/6 6
6
( 5
i/6)
6
12
5i
.
26.
2.3
2 2i .
Записываем число в показательной форме
3
2 2i = 8 e
i (3 /4 2 k )
| 2 2i |= 4 4 = 8.
.
При извлечении корня 3-ей степени
получим 3 значения корня.
Записываем выражение для вычисления
всех корней
3
i =3
i (3 /4 2 k )
3
8e
= 2 ei ( /4
и перебираем значения
до
k
k = (n 1) = 3 1 = 2.
от
k =0
2 k/3)
27.
3i ( /4)
= 2
cos i sin =
k = 0 : = 2 e
4
4
2
2
= 2
i
= 1 i.
2
2
11
11
2 2i = k = 1 : 2 ei ( /4 2 /3) = 2
i sin
cos
12
12
1,4 ( 0,97 0,26 i ) 1,36 0,36 i.
19
19
k = 2 : 2 ei ( /4 4 /3) = 2
cos
i sin
12
12
1,4 (0,26 0,97 i ) 0,36 1,36 i.
28.
3.Вычислить
z1
z2
,
z1 z2
если
z1 = 1 2i, z2 = 3 4i.
Выполним сложение и умножение чисел в алгебраической форме
(1 2i )
( 3 4i ) 3 6i 4i 8i 2
=
(1 2i ) ( 3 4i )
2 2i
3 6i 4i 8 11 10i
,
2 2i
2 2i
а затем деление
(11 10i)( 2 2i ) ( 22
=
( 2 2i )( 2 2i)
42 2i
42 2
i
8
8
8
20i 22i 20i 2 ) 22 2i 20
2
2
( 2) 2
4 4
21 1
i 5,25 0,25i,
4
4
29.
Функции комплексного переменногоО п р е д е л е н и е. Если каждому значению комплексной переменной
z = x iy
соответствует определенное значение комплексной переменной
w = u iv ,
то говорят, что переменная
и пишут
независимой переменной
z
w
есть функция
w = f ( z)
Аналогично тому, что задание комплексного числа равносильно заданию
пары действительных чисел, задание функции комплексной переменной
z
x
равносильно заданию двух функций пары действительных переменных
и
y
w = f ( z ) = u( x, y) iv( x, y)
u ( x, y ) Re w( z ), v( x, y ) Jm w( z ),
А именно:
Преобразования, целью которых служит нахождение функций
u ( x, y), v( x, y ),
называется выделением действительной и мнимой
частей функции комплексного переменного.
30.
1. w = z 2 u iv = ( x i y ) 2u iv = x 2 2i x y (i y ) 2 = ( x 2 y 2 ) i 2 xy, u = x 2 y 2 , v = 2 xy.
2. w =
z
z 3i
.
x iy
x iy
( x i y )( x i( y 3))
=
=
=
=
2
2
z 3i x i y 3i x i( y 3)
x ( y 3)
z
x 2 ixy ix( y 3) i 2 y ( y 3) x 2 y( y 3)
3x
=
= 2
i 2
.
2
2
2
2
x ( y 3)
x ( y 3)
x ( y 3)
x 2 y ( y 3)
3x
u= 2
, v= 2
.
2
2
x ( y 3)
x ( y 3)
31.
Основные элементарные функции1. Степенная функция
w=z
n
w = z 3 = ( x i y )3 = x3 3x 2 (iy ) 3x(iy ) 2 (iy )3 =
= x3 i3x 2 y 3xy 2 i 3 y 3 =
= x3 3xy 2 i3x 2 y i y 3 = ( x3 3xy 2 ) i (3x 2 y y 3 ),
u ( x; y ) = x3 3 xy 2 , v( x; y ) = 3 x 2 y y 3.
Отметим, что при
n 3
можно пользоваться алгебраическим
представлением комплексного числа, а при больших значениях
показателя степени -- тригонометрическим или показательным.
32.
2. Показательная функцияw = e z = e x
iy
z
w=e
= ex
ei y = e x
(cos y isin y ).
Выделяем действительную и мнимую части функции
Ree z = e x cos y, Ime z = e x sin y,
а также находим модуль и аргумент
| e z |= e x ,
arg e z = y.
Основные правила
z1 z2
e
=
z1 z2
e e .
e
z1 z 2
=
e
z1
e
z2
,
e
z n
nz
=e .
Вычислим значения функции в некоторых точках
1. ei /2 = cos /2 i sin /2 = i.
2. e i = cos1 i sin 1 = 0,54 0,84i.
3. e 2
5i
= e 2 (cos 5 isin 5) 7.39(0,28 0,96i ) 2,07 7,09i.
33.
w = ln z3. Логарифмическая функции
z = x iy
Если комплексную переменную
w = Ln z
и
представить
в показательной форме
z =| z | ei Arg z =| z |
ei ( 2 k )
| z |= x 2 y 2 , модуль
, где
= arg z
аргумент числа
w = Ln z = Ln| z | ei Arg z = ln | z |
ei ( 2 k ) = ln | z | i( 2 k ).
w = ln z = ln | z |
ei arg z = ln | z | iarg z = ln| z | i .
Ln z = ln| z | i(arg z 2
k ),
Действительная часть функции
мнимая --
ln z = ln | z | iarg z
u( x; y) = ln | z |,
v( x; y) = Argz.
w = ln z
-- главное значение логарифма при
k =0
34.
Свойства логарифмов:ln( z1z2 ) = ln z1 ln z2 , ln( z1/z2 ) = ln z1 ln z2 ln z = ln z.
Задача. Вычислить значения логарифмов
1. Ln( 1
3i ) =|
| 1
3i |= 1 3 = 2,
arg ( 1
3i ) = 2 /3
|=
= ln 2 i(2
/3 2
k ) 0,69 i(2,09 6,28k ), (k = 0; 1; 2;...).
2. ln ( 6) =|
| 6 |= 6,
|= ln 6 i 1,79 3,14i.
arg ( 6) =
35.
4. Тригонометрические функцииw = sin z, w = cos z, w = tg z, w = ctg z.
Эти функции определяются через функцию
w = ez
по формулам Эйлера
eiz e
sin z =
2i
,
sin z 1 eiz e
tg z =
= iz
cos z i e e
Функции
w = sin z
и
eiz e
cos z =
2
iz
iz
iz
,
iz
.
cos z eiz e
ctg z =
= i iz
sin z
e e
w = cos z
iz
iz
.
не являются ограниченными
и в этом их самое существенное отличие от обычных тригонометрических
функций.
36.
Вычислим значения тригонометрических функций.ei ( i ) e
sin(
i) =
2i
i(
i)
ei (3
e e
i
=
(0,04 23,10) 11,58i.
2i
2
e i (3 2i )
cos(3 2i ) =
= 0,5[e 2 e 3i e 2e 3i ] =
2 2
2
= 0,5[e (cos 3 i sin 3) e (cos 3 i sin 3)] =
= 0,5[cos 3(e 2 e 2 ) i sin 3(e 2 e 2 )] = 3,72 0,51i.
2i )
5. Гиперболические функции
w = sh z, w = ch z, w = th z, w = cth z.
e z e
sh z =
2
z
e z e z
sh z
ch z
, ch z =
, th z =
, cth z =
.
2
ch z
sh z
37.
Справедливы следующие соотношенияsin (iz ) = ish z ,
cos(iz ) = ch z ,
sh(iz ) = i sin z ,
tg (iz ) = i th z ,
ch 2 z sh 2 z = 1,
ch(iz ) = cos z ,
ctg (iz ) = icth z ,
sh 2 z ch 2 z = ch2 z.
С помощью гиперболических функций можно записать формулы
sin z = sin ( x i y ) = sin xch y icos xsh y,
cos z = cos( x i y ) = cos xch y isin xsh y,
Эти формулы применяются для вычислений тригонометрических и
гиперболических функций
38.
Вычислить значения:i
1. sh = i sin = i,
2
2
2. chi = cos = 1.
e (1 2i ) e
3. sh(1 2i) =
2
(1 2 i )
=
e1e
2i
e 1e 2i
=
2
e1 (cos 2 i sin 2) e 1 (cos 2 i sin 2)
=
2
0,98 2,81i
0,49 1,4i.
2
4. cos(3 2i ) = cos 3
ch2 i sin 3
sh 2
0,99
3,76 i
0,14
3,63 3,72 0,51i.
39.
Линии и области на комплексной плоскостиЗадача. Построить линии, заданные
соотношениями
z 2
1. |
|= 3.
z i
|
z 2
|= 3 | z 2 |= 3 | z i |
z i
| z 2 |= 3 | z i | | x i y 2 |= 3 | x i y i | ( x 2)2 y 2 =
= 3 x2 ( y 1)2 x2 4 x 4 y 2 = 9(x2 y 2 2 y 1)
8 x 2 8 y 2 4 x 2 y 4 = 0 ( x 1/4)2 ( y 9/8)2 = 45/64.
Центр окружности
O
( 1/4; 9/8)
Радиус
45/64 0,84.
40.
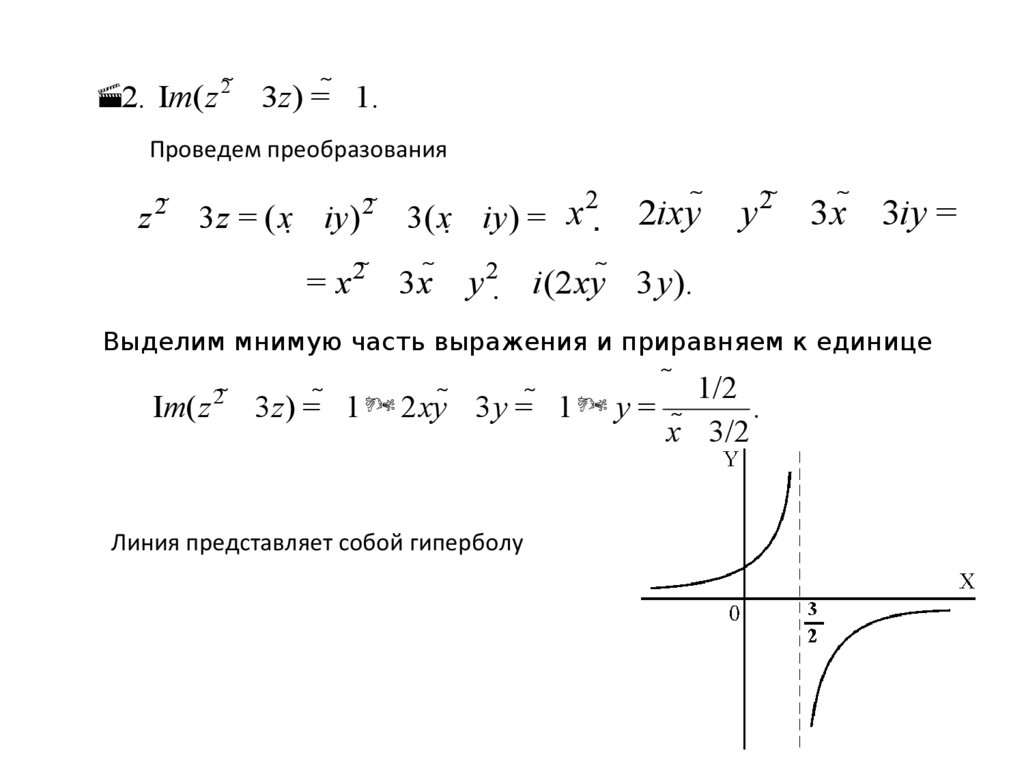
2. Im( z 2 3z ) = 1.Проведем преобразования
2
2
x
2
ixy
y
3 x 3iy =
z 3z = ( x iy ) 3( x iy ) =
2
2
= x 2 3x y 2 i (2 xy 3 y ).
Выделим мнимую часть выражения и приравняем к единице
1/2
Im( z 3z ) = 1 2 xy 3 y = 1 y =
.
x 3/2
2
Линия представляет собой гиперболу

















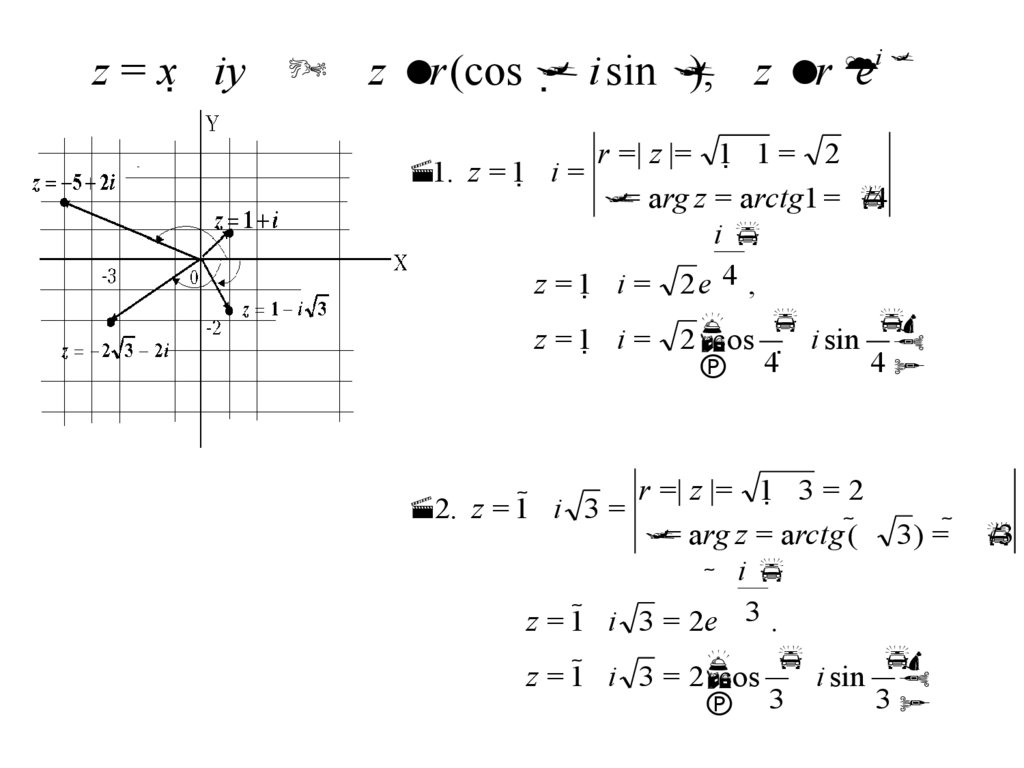


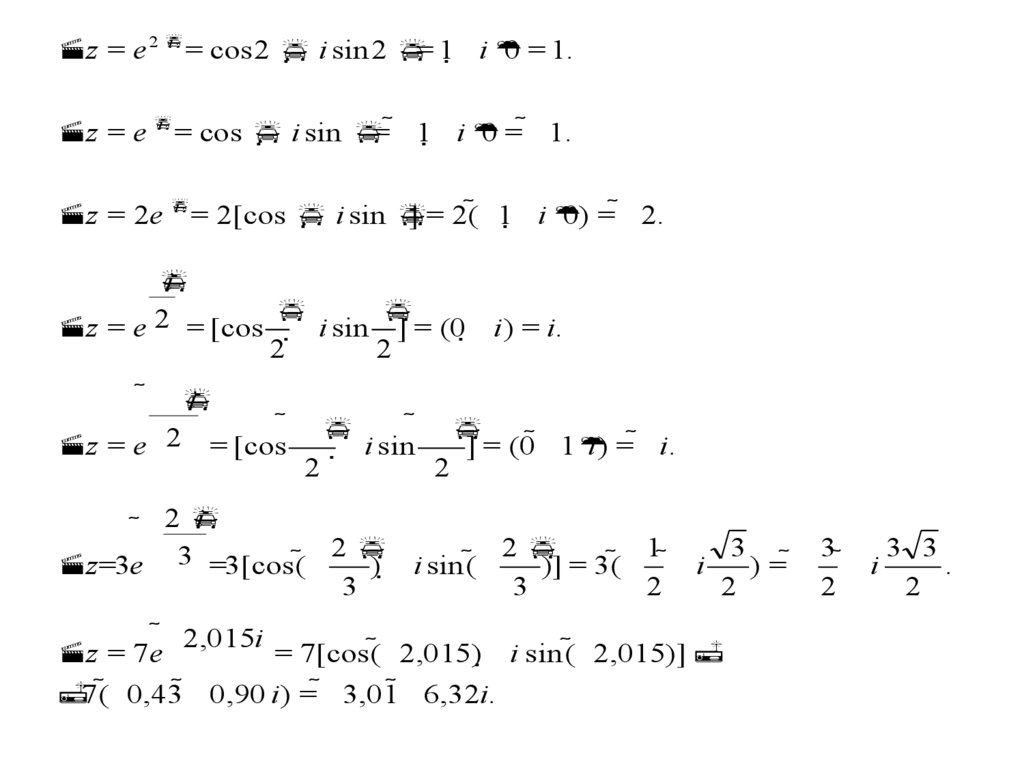






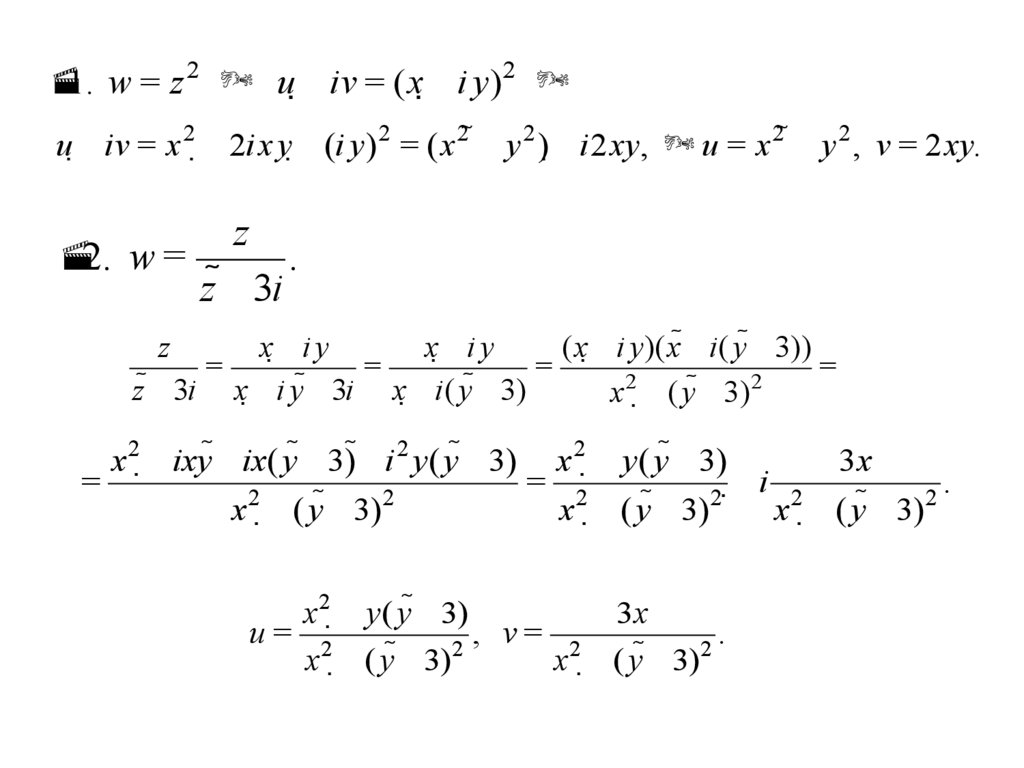









 mathematics
mathematics








