Дифференцирование функций комплексной переменной. Понятие аналитической функции

1. §4. Дифференцирование функций комплексной переменной. Понятие аналитической функции.

Пусть f(z) C(g).
Def. f(z) называется дифференцируемой (или
моногенной) в точке z0 g, если при z 0
def
f
( z z-z0) конечный предел lim
f ( z0 );
z 0 z
f z0 z f z0
f ( z0 ) lim
.
z
z 0
Не зависит от способа стремления
z 0 !

2.

Теорема 4.1 Если f z u x , y iv x , y
дифференцируема в точке z0 x0 iy0 , то
в точке x0 , y0 u x , u y , v x , v y :
u x v y , u y v x условия Коши-Римана.
Доказательство.
z x i y;
1) z x :
f
x u x0 , y0 i x v x0 , y0
lim
lim
x
x 0 x x 0
u x x0 , y0 iv x x0 , y0 *
* .

3.

2 ) z i y :
y u x0 , y0 i y v x0 , y0
f
* lim
lim
i y
y 0 i y y 0
i u y x0 , y0 iv y x0 , y0
v y x0 , y0 iu y x0 , y0
u x v y , u y v x .
(**).

4.

Пусть f(z) C(g), f z u x , y iv x , y .
Теорема 4.2 Если в точке z0 x0 , y0 g
du, dv и u x v y , u y v x , то f z
дифференцируемая в точке z0 .
Доказательство. du x0 , y0
u u x x0 , y0 x u y x0 , y0 y x , y ,
lim
z 0
( x, y)
z
0;

5.

dv x0 , y0
v v x x0 , y0 x v y x0 , y0 y x , y ,
( x, y)
lim
0;
z 0 z
Обозначим x , y x , y i x , y .
f u x x u y y iv x x iv y y ( x , y )
z
x i y
z
u x v y , u y v x
u x x v x y iv x x iu x y ( x , y )
x i y
z

6.

u x x i y iv x x i y ( x , y )
x i y
z
( x, y)
u x x0 , y0 iv x x0 , y0
z
f
lim
u x x0 , y0 iv x x0 , y0 f ( z0 ).
z 0 z
u x v y , u y v x :
1. f ( z ) u x x , y iv x x , y
v y x , y iv x x , y u x x , y iu y x , y
Замечания.
v y x , y iu y x , y .

7.

2. Теорема 4.2 не обратная к теореме 4.1
f
3. lim
f ( z0 )
z 0 z
f
0 :
f ( z0 ) , z .
z
Если f(z) дифференцируема в точке z0, то она
и непрерывна в этой точке.
Обратное, вообще говоря, неверно.
Пример.
f ( z ) z , z0 0.

8.

Основное определение. f(z) дифференцируемая
в z g, f ’(z) C(g) называется
аналитической функцией в g.
Обозначение:
f z C
g .
Понятие аналитичности функции определяет
глобальное поведение f(z) в области g.
Теорема 4.3 Необходимым и достаточным
условиями
f z u x , y iv x , y C
g .
являются u x , u y , v x , v y C g и
u x v y , u y v x условия Коши-Римана.

9.

Доказательство.
Необходимость. f z C
g f z C g
'
u x , u y , v x , v y C g .
Из Т.4.1 => u x v y , u y v x .
Достаточность. u x , u y , v x , v y C g
du, dv . Из Т.4.2 т.к. u x v y , u y v x
f z u x iv x .
'
Т.к. u x , v x C g f z C g .
'

10.

Замечание. Далее будет показано, что из
'
f z C
g f z C g .
Основное замечание. Условие f z C g
—лишнее.
'
Альтернативное определение.
f(z) дифференцируемая в z g, называется
«аналитической» функцией в g.
Вместо Теорем 4.2 и 4.3 будут

11.

Теорема 4.4 Если u x , y , v x , y C g и
в точке z0 x0 , y0 g u , u , v , v :
x y x y
u x v y , u y v x , то f z
дифференцируемая в точке z0 .
Теорема 4.5 Необходимым и достаточным
условиями «аналитичности» f z u iv в g
являются
u x , y , v x , y C g и
u x , u y , v x , v y : u x v y , u y v x z g .

12.

Оказывается, что производная
«аналитической» функции непрерывна в g,
причем для n f(n)(z) C(g), т.е. класс
«аналитических» функций не является
расширением введенного нами класса, а
полностью с ним совпадает.

13. Следствия условий Коши-Римана

f z u x , y iv x , y C
g .
1. u u xx u yy 0; v v xx v yy 0;
Обратно, пара гармонических в g функций
u(x,y) и v(x,y), связанные условиями КошиРимана, являются действительной и мнимой
частью аналитической функции.

14.

2. z re
i
, f z u r , iv r , C
1
1
ur v , vr u .
r
r
3.
f z R x , y e
i ( x , y )
.
Rx R y , R y R x .
g .

15. Свойства аналитических функций.

1. f z C
g f z C g .
f1
2. f1 , f 2 C g f1 f 2 , f1 f 2 , C g .
3. w f z C
f2
g , w G , w C G
F ( z ) f z C g .

16.

4. f z u x , y iv x , y C g , f z0 0
z0 g . Тогда в w0 : w w0
'
w0 f z0 z w C w0 :
z w
1
.
w0
z0 , w0
'
f w0
Доказательство. Для z w
необходимо, чтобы в z0
u u x , y x x u , v
v v x , y y y u, v
'

17.

Для этого достаточно, чтобы в z0
ux
vx
uy
ux
0. Но
vy
vx
uy
uxv y u yv x .
vy
2
2
2
'
=(Коши-Риман)= u x v x f z0 0.
Доказано обратной функции z= (w).
z
1
Cоставим разностное отношение
w w
z
и непрерывность '(w0) при условии
'
f z0 0.

18.

5. Пусть в односвязной области g плоскости
(x,y) задана функция u x , y Re f z C g ,
Тогда v x , y Im f z C g , определяется
с точностью до аддитивной постоянной.
Доказательство.
dv v x dx v y dy { K . P .} u y dx u x dy
v x , y можно определить по dv
с точностью до аддитивной постоянной.

19.

x, y
x0 , y0
x , y0
v x , y u y dx
x 0 , y0
x, y
u x dy
x , y0
x , y0
x
y
x0
y0
u y x , y0 dx u x x , y dy .

20.

6. f z C z0 можно восстановить
z z* z z*
*
0
0
f z 2u
,
C0 ,
2
2
i
C0 f z0 .
z z* z z*
*
0
0
f z 2iv
,
C0 ,
2
2
i
7. grad u u x , u y , grad v v x , v y
grad u, grad v u x v x u y v y u y v y u y v y
0. Т.к. grad линии уровня => линии уровня
u(x,y)=c и v(x,y)=c взаимно .

21. Геометрический смысл модуля и аргумента производной аналитической функции.

w f z C
g , f z0 0 z0 g
'
w
i
f ( z0 ) lim
ke , k 0, R.
z 0 z
'

22.

z0 z
z0
1
z
arg z
g Z
w f z
w0 w
w
arg w
w0
1
G W

23.

1
z0
2
1
w f z
1
w0
1
2

24.

w
i
f ( z0 ) lim
ke , k 0, R
z 0 z
'
2
w k z o z ,
Свойство постоянства
растяжения.
k f z0 не зависит от выбора
'
f z0
'
При отображении w f z C g , f z0 0
Геометрический смысл
z0 g
'
бесконечно малые линейные элементы
преобразуются подобным образом, причем
f z0 коэффициент преобразования подобия.
'

25.

w
i
f ( z0 ) lim
ke , k 0, R
z 0 z
'
arg f ( z0 ) lim arg w lim arg z
'
z 0
z 0
1 1 1 1 .
'
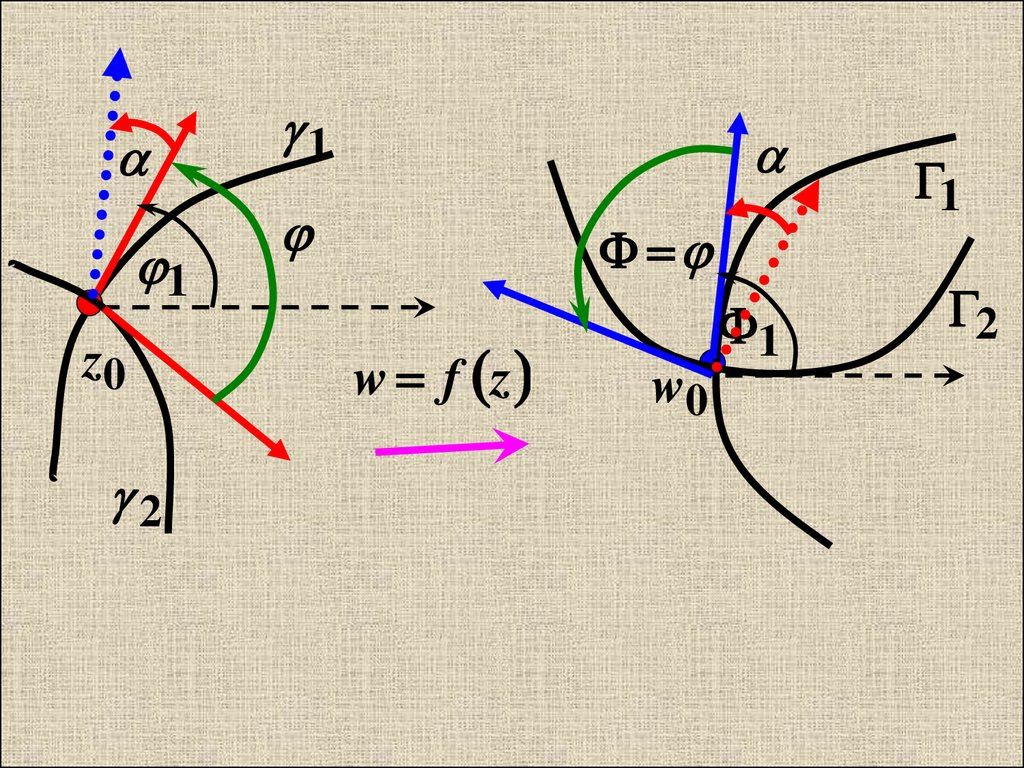
Геометрический смысл arg f ( z0 ) :
'
Аргумент производной arg f ( z0 ) в точке z0
определяет величину угла, на который нужно
повернуть касательную к гладкой кривой ,
проходящей через точку z0, чтобы получить
касательную к образу этой кривой в точке
w0=f(z0).

26.

arg f ( z0 ) не зависит от выбора 1 =>
'
для 2 : z0 2 : 2= 2+ => = 2- 1= 2- 1=
(сохраняется величина и направление углов).
Свойство сохранения углов.

27. Примеры простейших функций комплексной переменой.

'
1. f z const C
Z , f z 0.
'
2. f z az b C Z \ , f z a .
1
1
'
3. f z C Z \ 0 , f z .
2
z
z
n
'
n 1
4. f z z C Z \ , f z nz
,
n целое
5. f z z x iy C , u x 1 v y 1.
*