Similar presentations:
Многочлены от одной переменной
1. 2.1. Многочлены от одной переменной
• Многочлены.• Делимость многочлена.
• Теорема Безу.
• Схема Горнера.
• Корни многочлена.
2. 1.1. Многочлены
• Выражение вида:a0 x a1 x
n
n 1
a2 x
n 2
... a n 1 x a n
• называется многочленом степени n
одного аргумента (переменной).
• Будем обозначать многочлен одной
переменной через
• P x , Q x ,
…
3.
• Степенью многочлена называетсянаивысшая степень аргумента
многочлена.
• Для указания степени многочлена
будем использовать нижний индекс
заглавной буквы: Pn x .
4.
• ЗаписьPn x a0 x n a1 x n 1 a 2 x n 2 ... a n 1 x a n
• представляет собой стандартный вид
многочлена одной переменной х
степени n, где
• a0 , a1 , ..., an 1 , an – коэффициенты
• степеней переменной х.
5. Определение 1.
• Два многочленаPn x
и
Qn x
,
• называются равными,
• если их коэффициенты
• при соответствующих степенях х
равны,
6.
• т.е. пустьn
n 1
n 2
P
x
a
x
a
x
a
x
... a n 1 x a n
• n
0
1
2
,
n
n 1
n 2
• Qn x b0 x b1 x b2 x ... bn 1 x bn ,
• тогда Pn x Qn x
• a0 b0 ,
a1 b1
,…
a n bn
.
7.
• Многочлен Qm x• называется многочленом степени
• выше чем многочлен Gk x
,
• если наивысший показатель степени
х многочлена Qm x
• больше наивысшего показателя
степени х многочлена Gk x
• т. е.
m k
8.
• МногочленыQm x
и
Gk x
• называются многочленами
одинаковой степени, если
m k
.
9. Основные формулы сокращенного умножения:
• (a b) 2 a 2 2ab b 2 ;• (a b) 2 a 2 2ab b 2 ;
• (a b) a 3a b 3ab b ;
3
3
2
2
3
• (a b) 3 a 3 3a 2 b 3ab 2 b 3 ;
• a 2 b 2 (a b)(a b)
;
• a b (a b)(a ab b );
3
3
2
2
• a 3 b 3 (a b)(a 2 ab b 2 ) ;
10. 1.2. Деление многочлена на многочлен
• Любой многочлен может бытьпредставлен в виде:
Pn x Qm x Gk x R x ,
• где
• Qm x
– делитель многочлена P x ,
n
• Gk x – частное от деления многочлена
• Pn x на многочлен Qm x ,
11.
• R x – остаток от деления многочлена• Pn x на многочлен Qm x .
• Причем, сумма степеней делителя и
частного равна степени делимого,
• т. е.
m k n
,
• степень остатка меньше степени
делителя.
12. Определение 1.
• МногочленPn x
• делится на многочлен
Qm x
,
• если остаток от деления равен нулю,
• т.е.
R x 0
.
13. Пример 1.
• Найти частное и остаток от делениямногочлена
• на
P4 x x 4 3x 3 5x 2 6 x 1
2
Q
x
x
3x 2 .
• 2
14. Деление столбиком.
• x4 + 3x3 - 5x2 + 6x – 1-x2 + 3x + 2
• x4 - 3x3 - 2x2
- x2 - 6 x - 15 = G2(х)
6x3 - 3x2 + 6x
6x3 -18x2 - 12x
15x2 + 18x - 1
15x2 - 45x - 30
63 x + 29 = R(x)
15. 1.3. Деление многочлена на двучлен
16. Теорема Безу
• При делении многочлена Pn x• на двучлен
x
• остаток от деления равен значению
многочлена при x ,
• т. е. R x Pn .
17. Доказательство.
• Пусть при делении многочлена Pn x• на двучлен
x
• имеем
• Pn x x Qn 1 x R x .
18.
• Подставим в полученное выражениезначение
x
,
• получим Pn Qn 1 R ,
• или
• или
Pn 0 Qn 1 R
Pn R
,
,
• что и требовалось доказать.
19. Определение 1.
• Корнем многочлена называетсятакое значение аргумента, при
котором значение многочлена
обращается в нуль.
20.
• Таким образом,x
• является корнем многочлена , Pn x
• если
Pn 0
.
21. Следствия из теоремы Безу
22. 1.
• МногочленPn x
• делится на двучлен x
• тогда и только тогда, когда число
является корнем многочлена .
x
23. Другими словами,
• если при делении многочлена• на двучлен
Pn x
x
• остаток R(x) от деления равен нулю,
• то значение
x
• – корень многочлена.
24. Доказательство.
• По теореме Безу• если R 0 ,
• то следовательно
,
Pn R
Pn 0
.
• По определению корня многочлена
имеем, что
x
• – корень многочлена, что и
требовалось доказать.





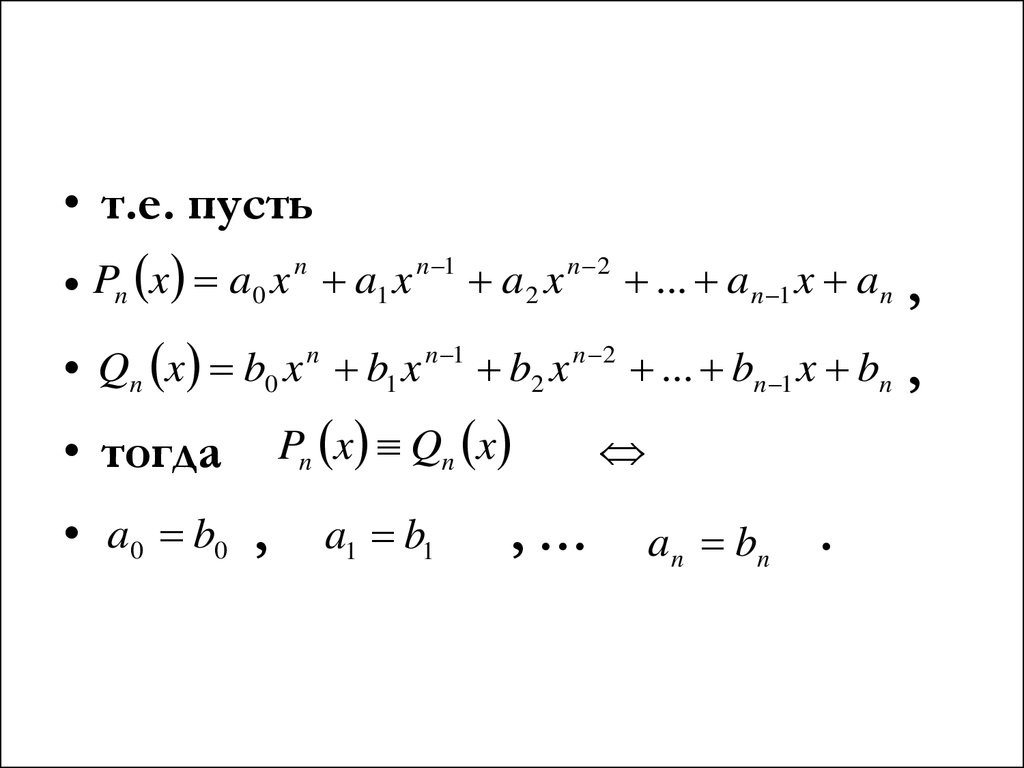







































 mathematics
mathematics








