Similar presentations:
Способы нахождения корней многочлена. Теорема Безу
1. Способы нахождения корней многочлена. Теорема Безу.
Выполнили:Студенты 1 курса группы ИМ-11
Зорин Александр Сергеевич
Шабунин Дмитрий Олегович
Г.Абакан
08.01.2016г
2. Цели
Познакомитьсяс историей образования
способов нахождения корней линейных и
квадратичных многочленов;
Понятие многочлена;
Схема Горнера;
Рассмотреть алгоритм решения кубических
и биквадратных уравнений;
Решения алгебраических уравнений 3-й и
4-й степени;
Теорема Безу.
3. Немного истории
Способ нахождения корней линейных иквадратичных многочленов, то есть способ
решения линейных и квадратных
уравнений, был известен ещё в древнем
мире.
4.
Омар Хайям(1048-1131гг)
Сципиона дель ФерроНикколо Фонтана Тарталья Джероламо Кардано
(1465-1526г)
( 1499—1557)
(1501–1576)
Поиски формулы для точного решения общего уравнения третьей
степени продолжались долгое время (следует упомянуть метод,
предложенный Омаром Хайямом), пока не увенчались успехом в первой
половине XVI века в трудах Сципиона дель Ферро,
Никколо Фонтана Тарталья и Джероламо Кардано.
5. Многочлены
Многочлен от одной переменной x – это выражение вида〖 a〗_n x^n+a_(n-1) x^(n-1)+⋯+a_1 x+a_0,
где x – переменная ,a_n,a_(n-1),…,a_0– коэффициенты из некоторого
числового поля, n – целое неотрицательное число, а нулевое- свободный
член.
Также многочлен называют «полиномом», этот термин происходит от
греческих слов «πολι» - много и «νομχ» - член.
Предполагается, что коэффициенты многочлена принадлежат
определенному полю (полю действительных, рациональных, комплексных
чисел).
совокупность всех многочленов с коэффициентами из данного поля Р
образует кольцо Р[х] - кольцо многочленов над данным полем, это кольцо
не имеет делителей нуля, т.е. произведение многочленов, не равных нулю,
не может дать нуль.
6. Что такое схема Горнера?
Схе́ма Го́рнера (или правилоГорнера, метод Горнера) —
алгоритм вычисления
значения многочлена,
записанного в виде суммы
мономов (одночленов), при
заданном значении
переменной.
Метод Горнера позволяет
найти корни многочлена, а
также вычислить производные
полинома в заданной точке.
Схема Горнера также является
простым алгоритмом для
деления многочлена на бином
вида . Метод назван в
честь Уильяма Джорджа
Горнера.
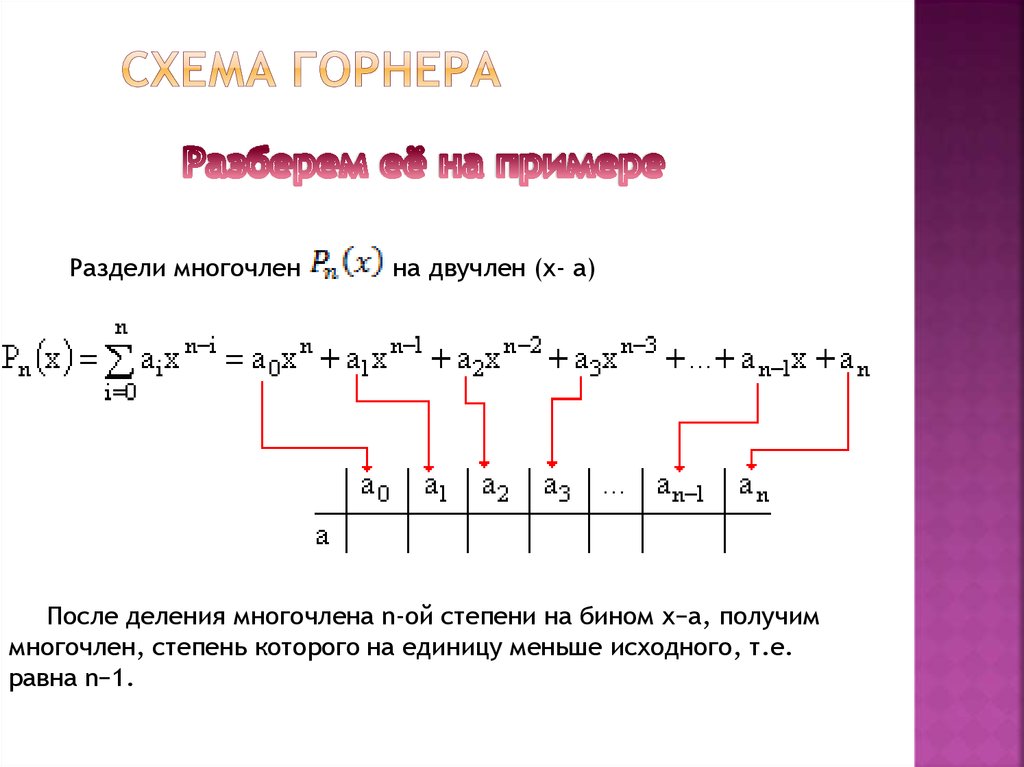
7. Схема Горнера
Раздели многочленна двучлен (x- а)
После деления многочлена n-ой степени на бином x−a, получим
многочлен, степень которого на единицу меньше исходного, т.е.
равна n−1.
8. Алгоритм решения кубического уравнения
Рассмотрим алгоритм решениякубических уравнений, когда x=0 является
корнем кубического уравнения
Ax3+Bx2+Cx+D=0
В этом случае свободный член D равен
нулю, то есть уравнение имеет вид
Ax3+Bx2+Сx=0
Если вынести x за скобки, то в скобках
останется квадратный трехчлен, корни
которого легко найти либо через
дискриминант, либо по теореме Виета
x(Ax2+Bx+C)=0
9. Пример решения кубических уравнений
Пример. Найти действительные корниуравнения 3x3+4x2+2x=0
Решение.
3x3+4x2+2x=0
x(3x2+4x+2)=0
x=0 является корнем уравнения. Найдем
корни квадратного трехчлена
3x2+4x+2
Так как его дискриминант D=42-4*3*2=-8
меньше нуля, то действительных корней
трехчлен не имеет.
10. Алгоритм решения биквадратного уравнения
Уравнениявида ax4 + bx2 + c = 0 будем
называть биквадратными уравнениями.
Биквадратное уравнение можно решить
заменой y=x2 свести к квадратному
уравнению y2+by+c=0.
А дальше решаем как квадратное
уравнения
После получения корней подставляем
вместо У x2
11. Пример решения биквадратного уравнения
Пример. Решить уравнение x4 - 10x2 + 1 =0.
Решение. Пусть y= x2, y2-10y+1=0,тогда
y1,2=5 ± √(24).
Решив совокупность неполных квадратных
уравнений
x2 =5+ √(24) и x2 =- √(24),
получим ответ.
Ответ:X1,2,3,4=±
√(5 ± √(24)).
12. Теорема Безу
довольнопросто в своем
использовании, но при этом
она является одной из
базовых теорем теории
многочлена. Она гласит,
что остаток от деления
многочлена f(x) на
многочлен (x-c) - это f(c).
f(x) – многочлен с
коэффициентами из кольца
P.
13. Доказательство:
Раздели многочлен f(x) на двучлен с остатком r.Получим
f(x) =(x-c)*s(c) +r .
Теперь подставим в получившееся равенство вместо
Получаем
x
число с.
f(c)=(c-c)*s(c) +r
Так как скобка (c-c)* равна нулю, то из этого следует, что
f(c)= r.
14. Источники
1.Биографический словарь деятелей в области математики
/ сост. Бородин А.И., Бугай А.С. — К.: Рад. школа, 1979.—
607 с.
2.
http://www.calc.ru/Teorema-Bezu-Skhema-Gornera.html
3.
http://math1.ru/education/raznoe/gorner.html
4.
Изображения взяты из Интернет-ресурса yandex
15. Спасибо за внимание конец
Выполнили:Студенты 1 курса группы ИМ-11
Зорин Александр Сергеевич
Шабунин Дмитрий Олегович














 mathematics
mathematics








