Основные свойства действительных чисел

1. Основные свойства действительных чисел

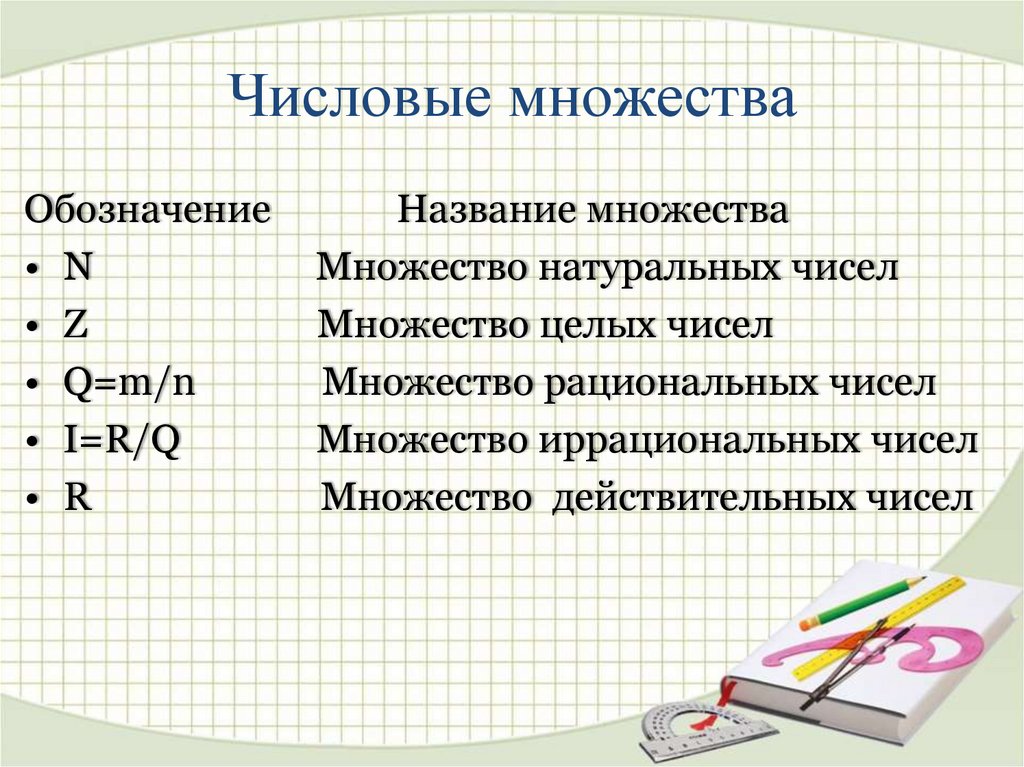
2. Числовые множества

Обозначение
• N
• Z
• Q=m/n
• I=R/Q
• R
Название множества
Множество натуральных чисел
Множество целых чисел
Множество рациональных чисел
Множество иррациональных чисел
Множество действительных чисел

3. Иррациональные числа

Иррациональные числа – это числа которые
m
невозможно представить в виде n , где m целое число, n – натуральное число.
Иррациональные числа – это бесконечные
непериодические десятичные дроби.
2 1,414213562...;
3 1,7320508075...;
π 3,14159...; e 2,7182845
- иррациональные числа.

4. Действительные числа

Все числа – рациональные и
иррациональные образуют множество
действительных чисел.
Это множество обозначается буквой R.
47
; 0;
7 ; 3 2 ; 100000
16
действител ьные числа.
5; 3; 1,678;

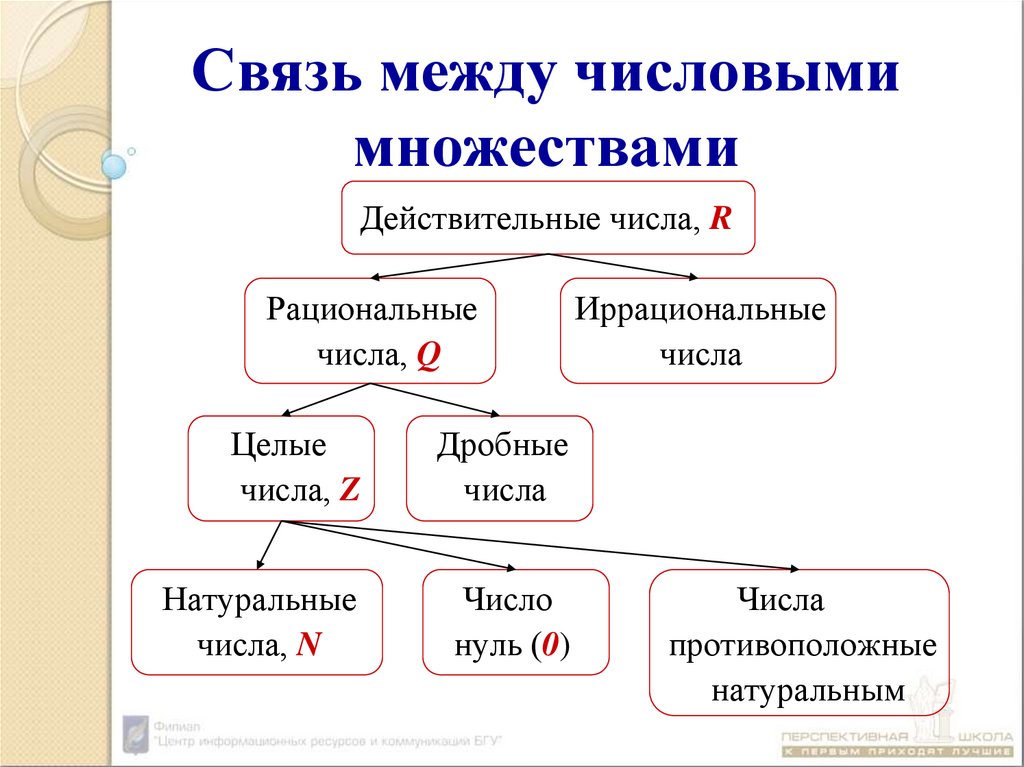
5. Связь между числовыми множествами

Действительные числа, R
Рациональные
числа, Q
Целые
числа, Z
Дробные
числа
Натуральные
числа, N
Число
нуль (0)
Иррациональные
числа
Числа
противоположные
натуральным

6. Действия над действительными числами

Над действительными числами можно
выполнять арифметические действия;
они удовлетворяют тем же свойствам, что и
действия над рациональными числами.
1.
2.
Сложение
a + b = b + a;
(a + b) + c = a + (b + c);
a + 0 = 0 + a = a;
a + (-a) = (-a) + a = 0.
Вычитание a – a = 0; a – 0 = a; 0 – a = -a;
(a + b) – c = (a – c) + b = a + (b – c);
a – (b + c) = (a – b) – c = (a – c) – b;
a – (b – c) = (a – b ) + c = (a – c) + b.

7. Действия над действительными числами

3.
Умножение
a ∙ b = b ∙ a;
(a ∙ b) ∙ c = a ∙ (b ∙ c);
a ∙ 0 = 0 ∙ a = 0;
a ∙ 1 = 1 ∙ a = а;
a ∙ (-1) = -1 ∙ a = -а.
4.
Деление
a : 1 = a; a : a = 1; a : (-1) = -a;
0 : a = 0;
a : (b ∙ c) = (a : b) : c = (a : c) : b;
a : (b : c) = (a : b ) ∙ c = (a ∙ c) : b.

8. Сравнение действительных чисел

Действительные числа можно сравнивать;
для них справедливы те же свойства неравенств,
что и для рациональных чисел.
1. Если а > b, то b < а.
2. Eсли а > b и b > c, то а > c.
3. Если а > b и с – любое число,
то а + с > b + с.
4. Если а > b и с > 0 , то ас > bс.
5. Если а > b и с < 0, то ас < bс.

9. Свойства действительных чисел

Каждому действительному числу а на
координатной
прямой
соответствует
единственная точка А с координатой а, и
наоборот , каждой точке А координатной
прямой соответствует единственное число а.
7
А
1
В
0
1
С
3
D
3,5
E x
Множество всех действительных чисел
называется числовой прямой.

10. Дома: П3.4. Выучить свойства. Решить: №146(1ст); 838(а).