Призма. Тема 19

1.

2.

Тема 19.
Призма

3.

План лекции
1. Основные понятия.
2. Понятие призмы.
3. Виды призмы.
4. Площадь и объем.

4.

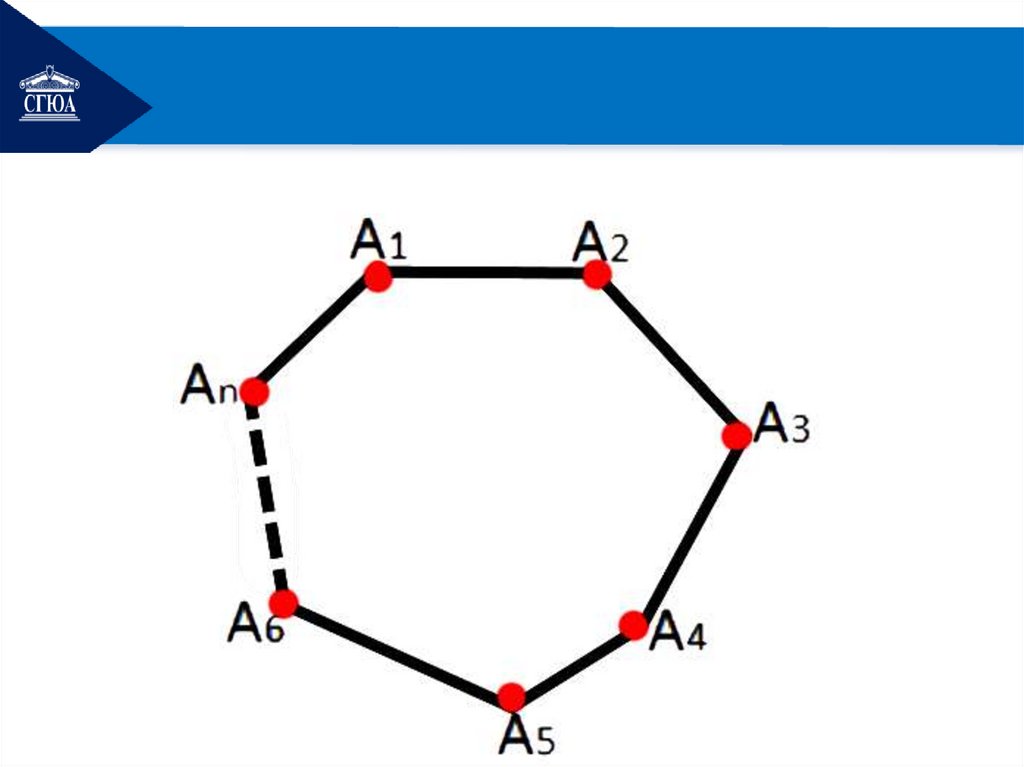
1. Основные понятия
Опр. Многоугольник – это
замкнутая линия, которая
образовывается, если
взять n каких-либо точек
A1 , A2 , A3 , An
и соединить их
последовательно отрезками.

5.

• Точки A , A , A , A
1
2
3
n
называются вершинами
многоугольника.
• Отрезки
A
,
A
,
,
A
23
n1
называются 12
сторонами
многоугольника.
Многоугольник с n сторонами
называют n-угольником.

6.

7.

Многоугольник называется
правильным, если все его
стороны равны.
Некоторые пространственные
фигуры, изучаемые в
стереометрии, называют
телами или геометрическими
телами.

8.

Мы будем изучать
геометрические тела, которые
называются
многогранниками.
Многогранником называется
геометрическое тело,
поверхность которого состоит
из конечного числа плоских
многоугольников.

9.

Многоугольники,
составляющие поверхность
многогранника, называются
его гранями; стороны
многоугольников – рёбрами;
вершины – вершинами
многогранника.

10.

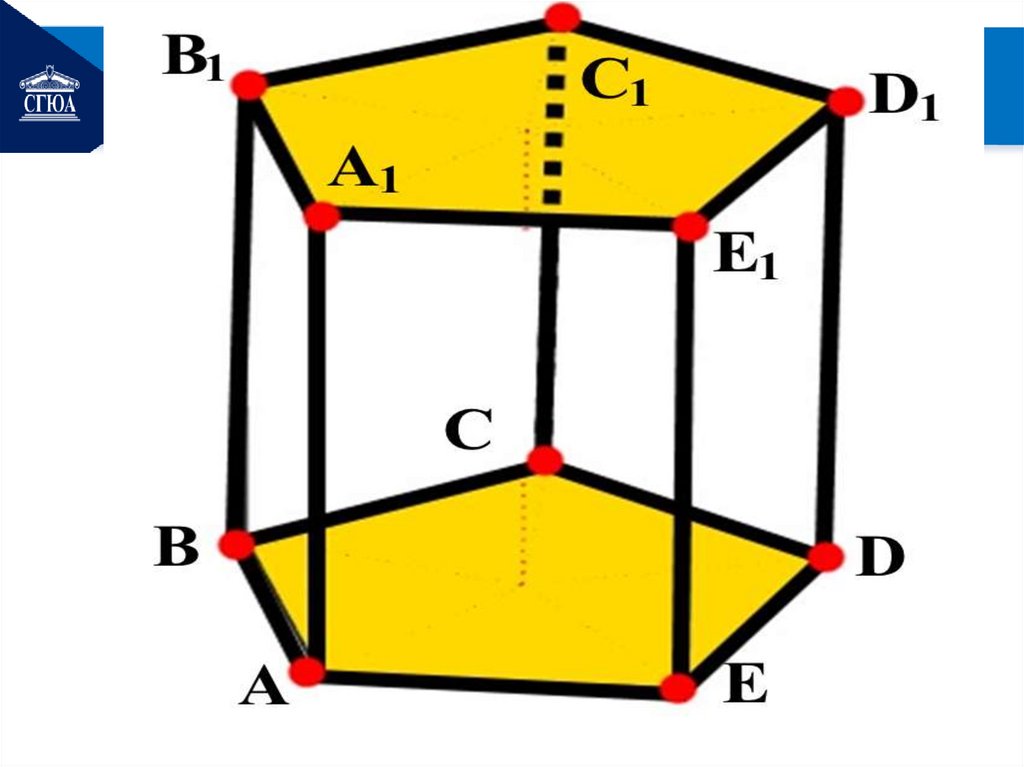
2. Понятие призмы
Опр. Призма – это
многогранник, две грани
которого являются равными
многоугольниками,
находящимися в
параллельных плоскостях, а
остальные грани –
параллелограммами.

11.

12.

Грани, которые находятся в
параллельных плоскостях,
называются
основаниями призмы, а
остальные грани – боковыми
гранями призмы.

13.

Свойства призмы
•Основания призмы равны и
лежат в параллельных
плоскостях.
• Боковые рёбра призмы
равны и параллельны.
•Основания призмы – это
равные многоугольники.

14.

Высотой призмы называется
любой из перпендикуляров,
проведённых из точки одного
основания к плоскости другого
основания призмы.
Диагональ призмы –это
отрезок, который соединяет
две вершины,
не принадлежащие одной
грани.

15.

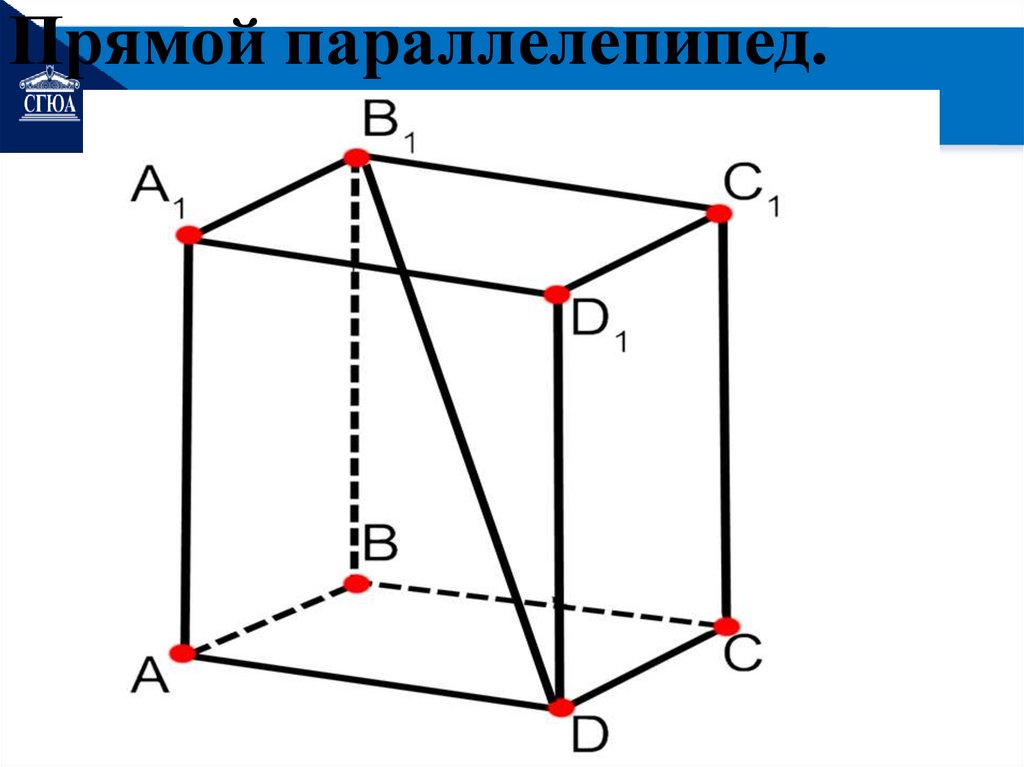
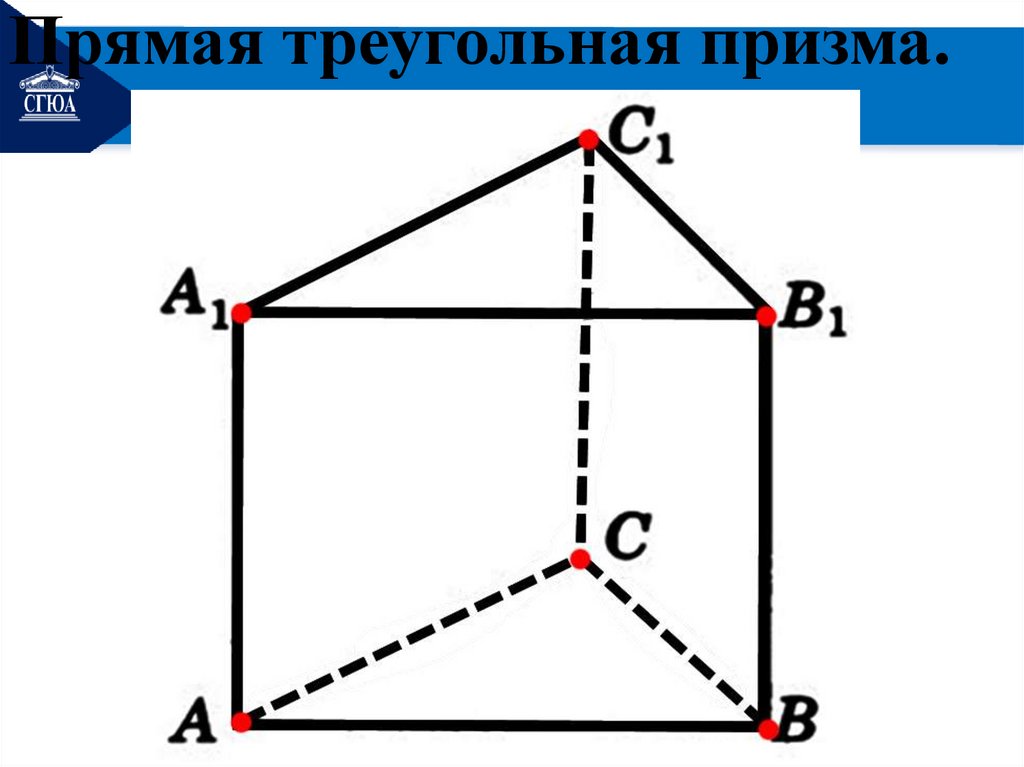
3. Виды призмы
1. Прямая призма.
Призма называется прямой,
если её рёбра
перпендикулярны плоскостям
оснований. Частным случаем
прямой призмы являются:

16.

Прямой параллелепипед.

17.

Прямая треугольная призма.

18.

Некоторые свойства.
•Боковые грани прямой
призмы – прямоугольники.
•Боковое ребро прямой
призмы является её высотой.
•Диагональ не существует
только у треугольной призмы.

19.

2. Прямая правильная призма.
Прямая призма называется
правильной, если её
основания являются
правильными
многоугольниками, то есть
квадратом, равносторонним
треугольником и т.д.

20.

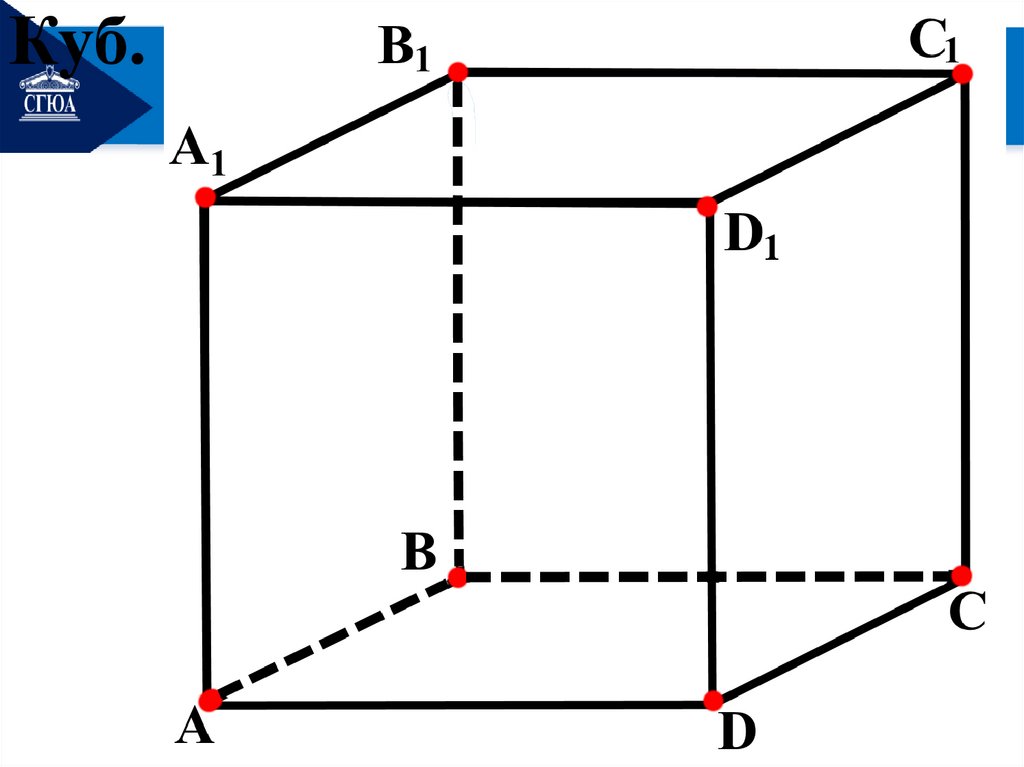
Куб.

21.

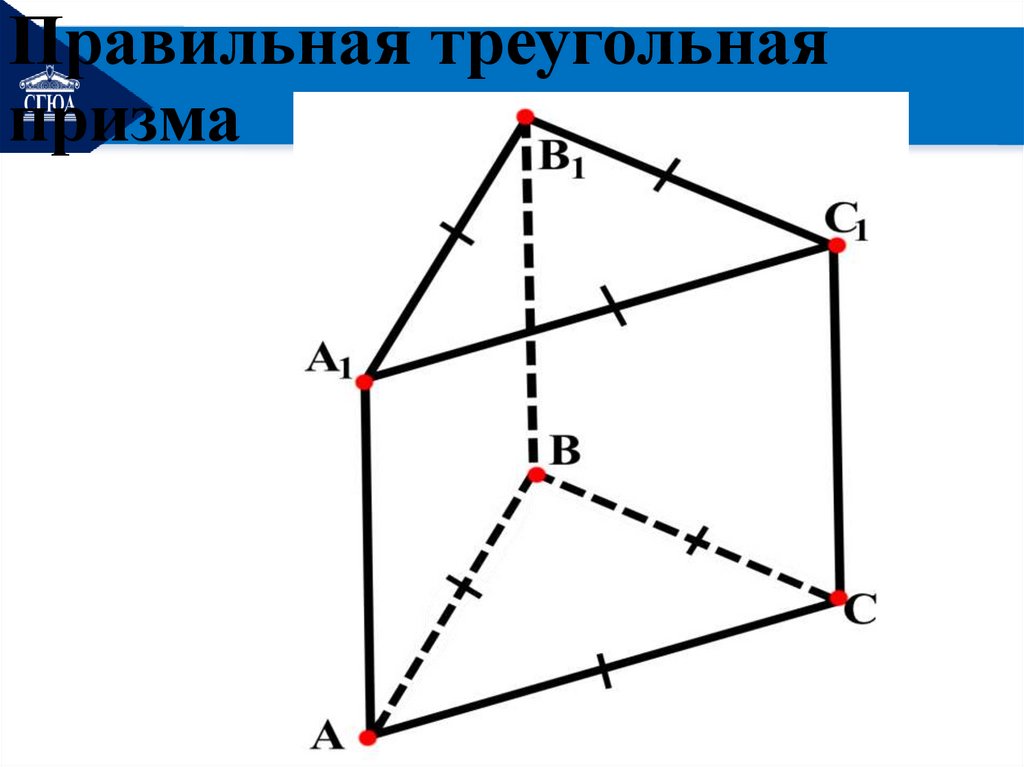
Правильная треугольная
призма

22.

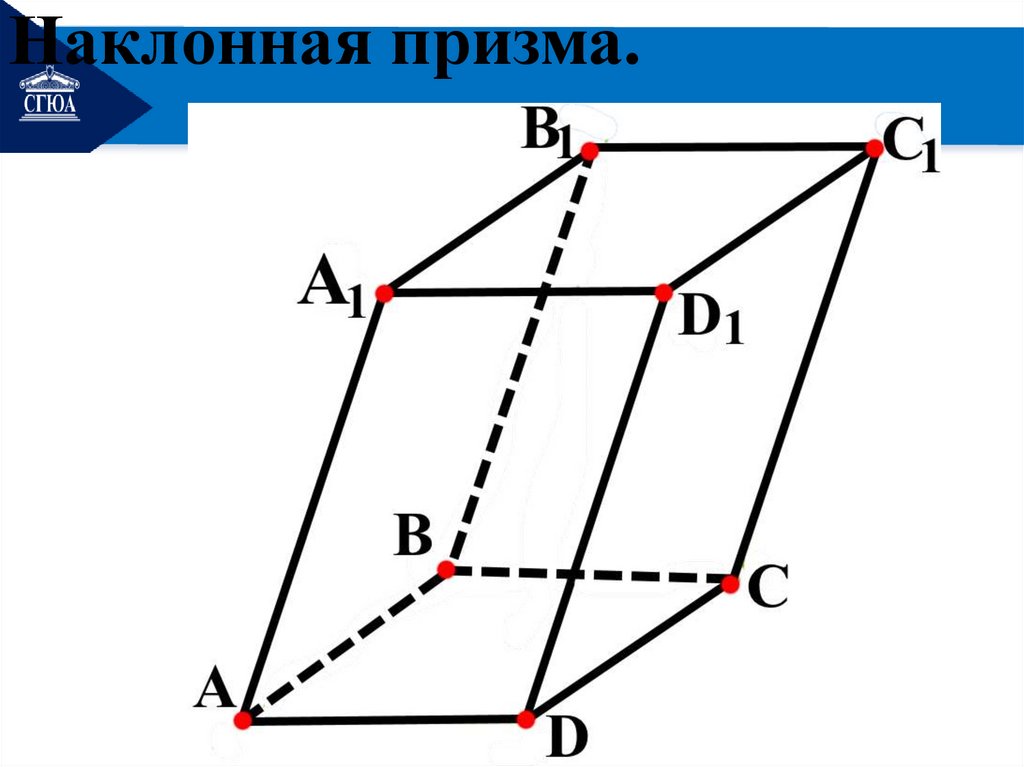
3. Наклонная призма.
Призма называется
наклонной, если её рёбра не
перпендикулярны плоскости
основания, то есть рёбра
образуют с плоскостью
основания произвольный
угол( не 90º).

23.

Наклонная призма.

24.

4. Площадь и объём
На практике будем работать с
прямой призмой.
Опр. Площадью боковой
поверхности призмы
называется сумма площадей
всех боковых ее граней.

25.

Теорема (Площадь боковой
поверхности призмы).
Площадь боковой поверхности
прямой призмы равна
произведению периметра
основания на высоту.
Sбок Pосн h

26.

Теперь рассмотрим полную
поверхность призмы.
Опр. Площадью полной
поверхности призмы
называется сумма площадей
всех её граней.

27.

Теорема(Площадь полной
поверхности призмы)
Площадь полной поверхности
прямой призмы равна сумме
площадей боковой
поверхности призмы и её
оснований.
S полн Sбок 2Sосн

28.

Теорема(Объём призмы).
Объём призмы равен
произведению площади
основания призмы на высоту.
Vпр S осн h