Действия с векторами

1. Действия с векторами

2. Сложение векторов

Правило «Треугольника»
Правило «Параллелограмма»
Правило «Многоугольника»

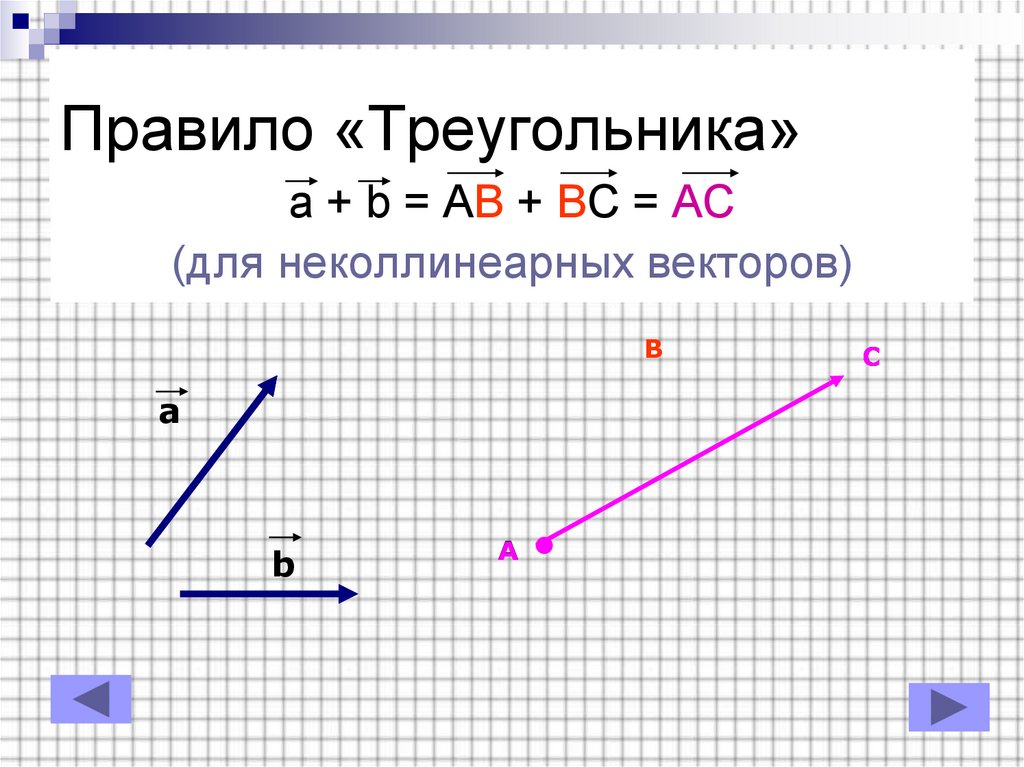
3. Правило «Треугольника»

a + b = AB + BC = AC
(для неколлинеарных векторов)
B
a
b
A
C

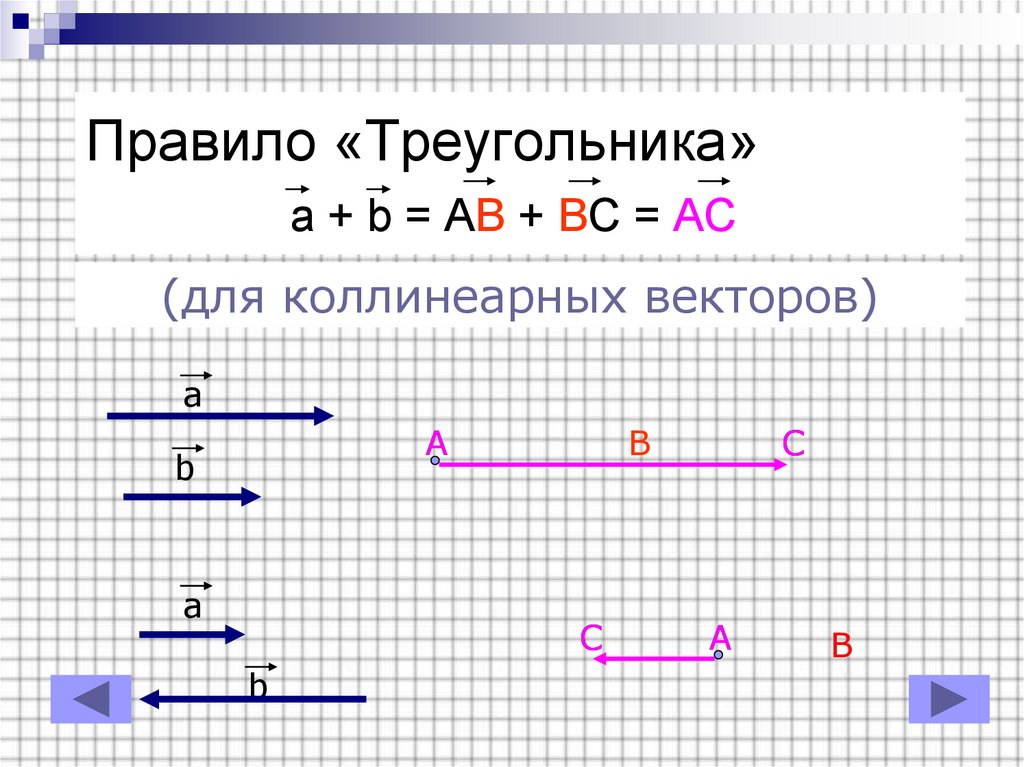
4. Правило «Треугольника»

a + b = AB + BC = AC
(для коллинеарных векторов)
a
A
b
a
B
C
b
C
A
B

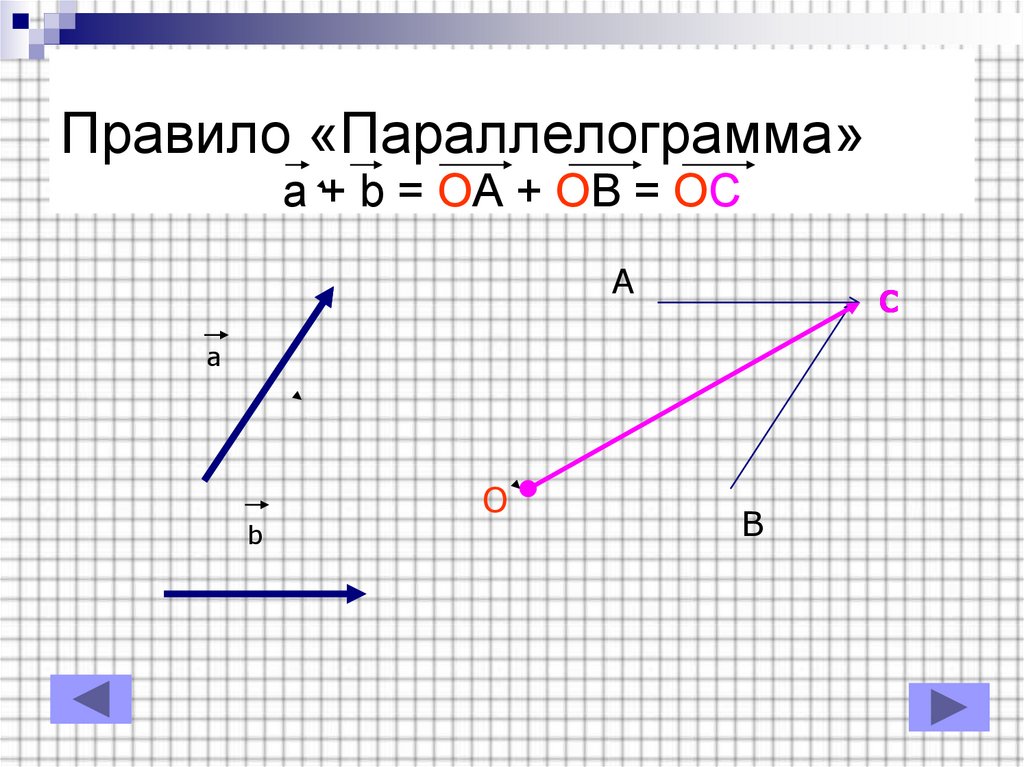
5. Правило «Параллелограмма»

a + b = OA + OB = OC
A
C
a
b
O
B

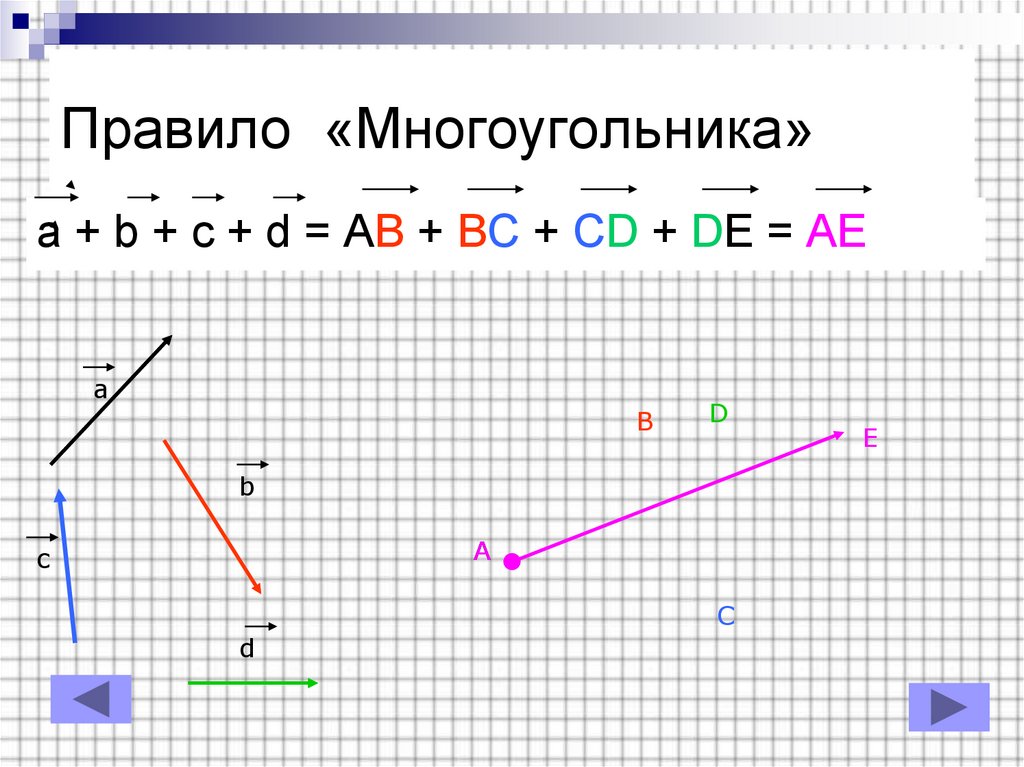
6. Правило «Многоугольника»

a + b + c + d = AB + BC + CD + DE = AE
a
B
D
b
A
c
C
d
E

7.

ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ
Для любых векторов а , в и с
справедливы равенства:
1) а + в = в + а --- переместительный
закон
2) ( а + в ) + с = а + ( в + с ) --сочетательный закон

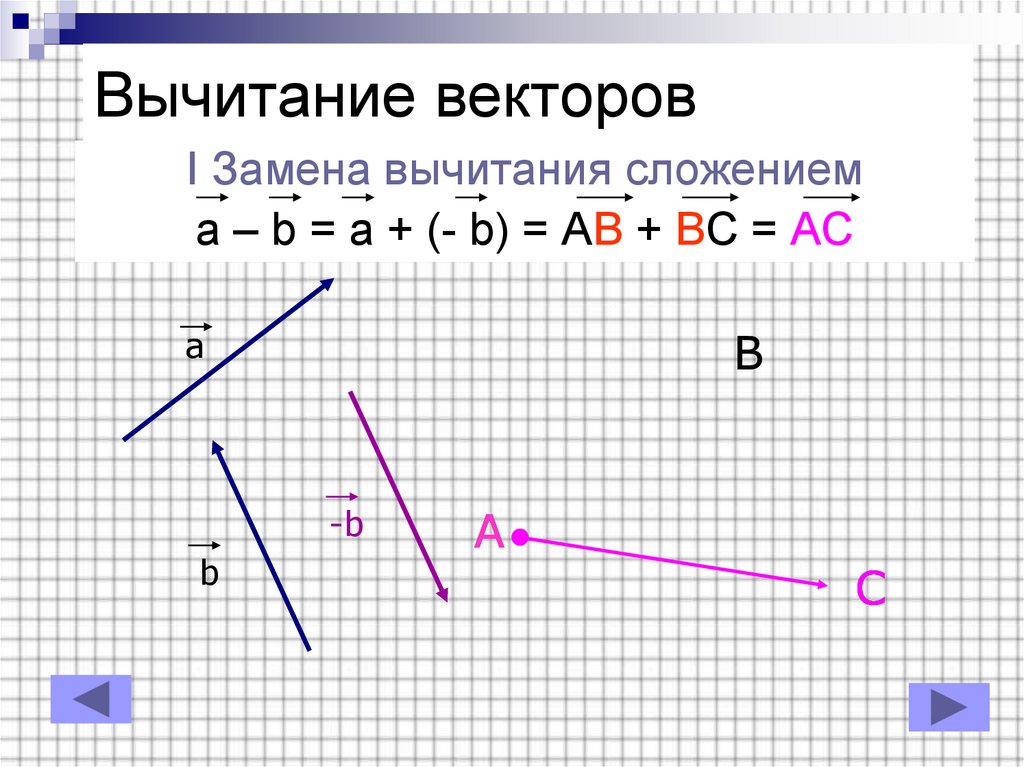
8. Вычитание векторов

I Замена вычитания сложением
a – b = a + (- b) = AB + BC = AC
B
a
-b
b
A
C

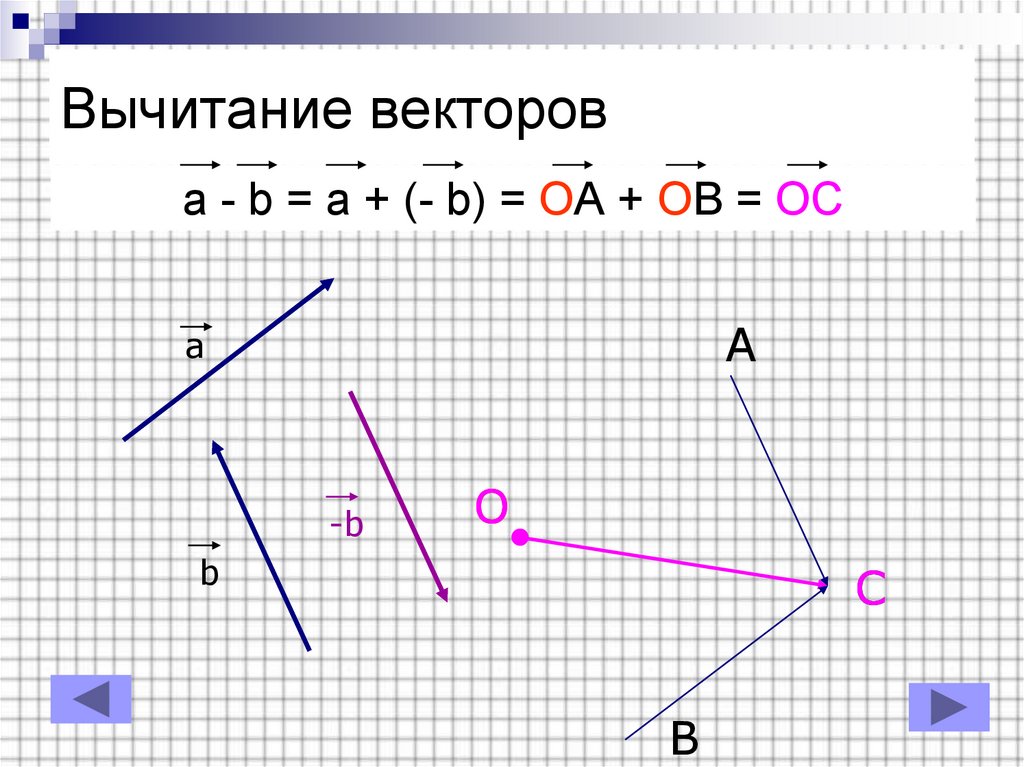
9. Вычитание векторов

a - b = a + (- b) = OA + OB = OC
A
a
-b
O
b
C
B

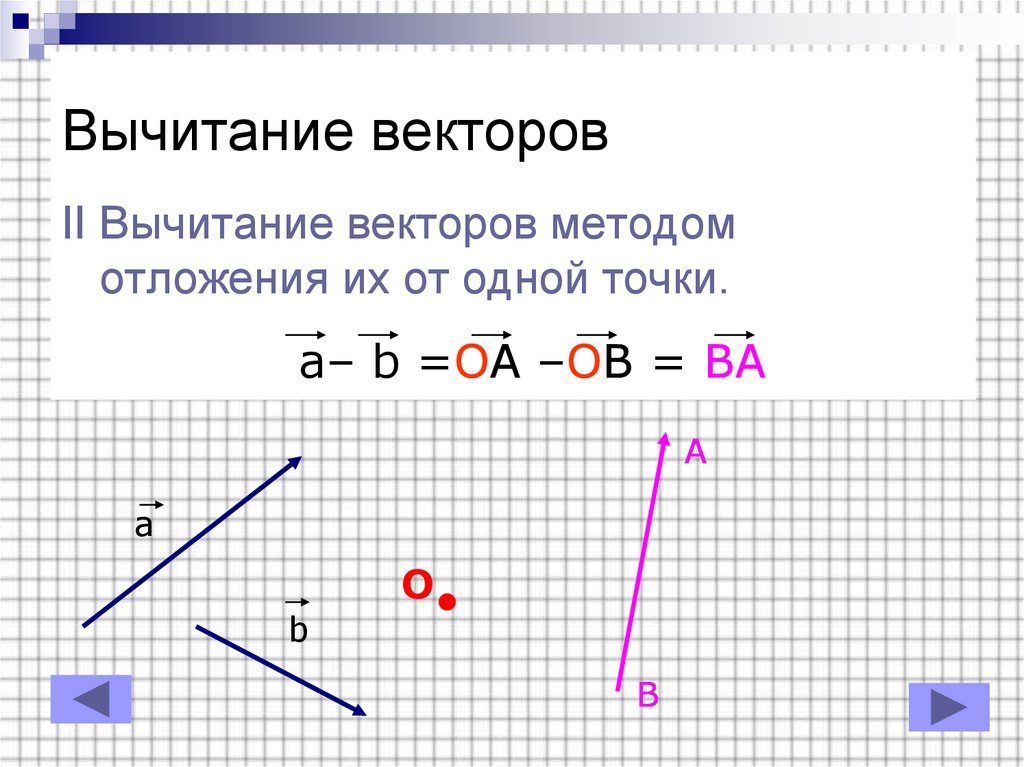
10. Вычитание векторов

II Вычитание векторов методом
отложения их от одной точки.
a– b =OA –OB = BA
A
a
O
b
B

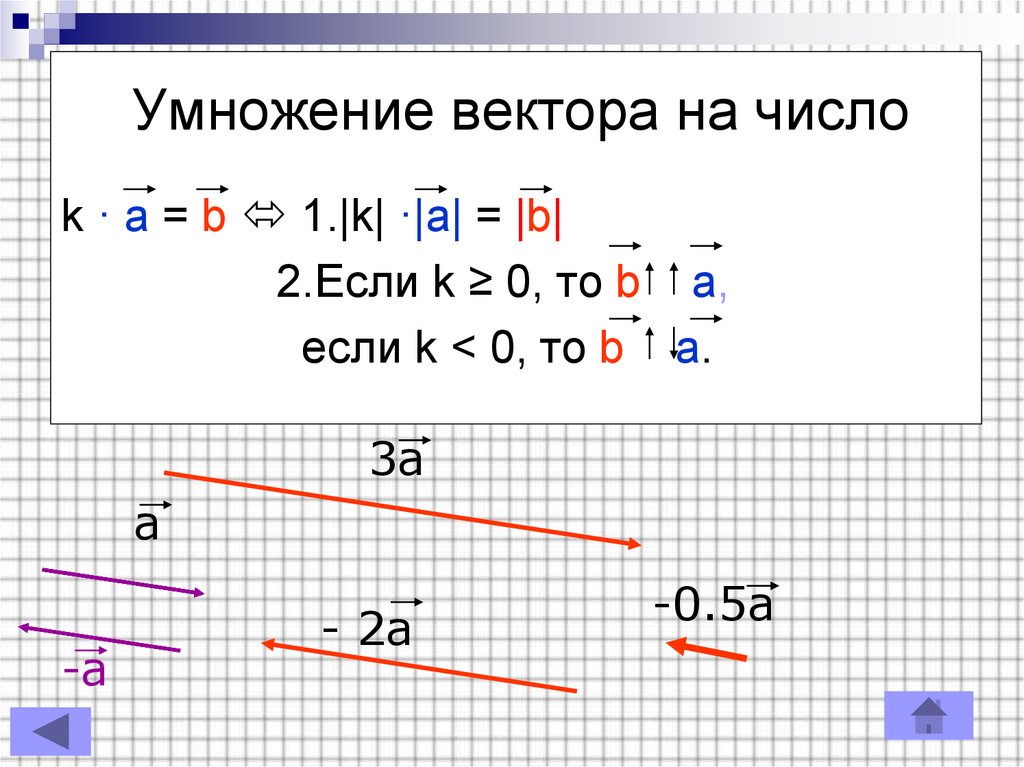
11. Умножение вектора на число

k · a = b 1.|k| ·|a| = |b|
2.Если k ≥ 0, то b a,
если k < 0, то b a.
3a
a
-a
- 2a
-0.5a

12. Свойства умножения векторов

Для любых векторов a и b и любых чисел
k и l справедливы равенства:
(kl) a = k (l a ) – сочетательный закон
k( a + b ) = k a + k b - I распределительный
(k + l) a = k a + l a - II распределительный