Similar presentations:
Средние величины. Тема 4
1.
Тема 4.Средние величины
2.
План лекцииСредняя, её сущность. Виды и
формы средних величин
2. Средняя арифметическая
3. Средняя гармоническая
4. Средняя геометрическая и
средняя квадратическая
5. Структурные средние
6. Прочие средние
1.
3.
Средний показательпредставляет собой
обобщенную характеристику
признака в статистической
совокупности в конкретных
условиях места и времени
4.
Важнейшее свойствосреднего показателя
заключается в том, что
он отражает то общее,что
присуще всем единицам
изучаемой совокупности
5.
Средний показательвыражает типичные
черты однотипных
явлений по одному из
варьирующих признаков
6.
Главное значение среднихпоказателей состоит в их
обобщающей функции, то
есть замене индивидуальных значений признака
средней величиной,
характеризующей всю
совокупность явлений.
7.
Если средняя величинаобобщает качественно
однородные значения
признака, то она является
типической
характеристикой признака в
данной совокупности
8.
Сущность среднегопоказателя можно
раскрыть через его
логическую формулу,
которая называется
исходным соотношением
средней (ИСС)
9.
ИСС =Суммарное значение осредняемого признака
Число единиц совокупности
10.
11.
12.
13.
средняя арифметическая;средняя гармоническая;
средняя геометрическая;
средняя квадратическая,
кубическая и т.д.
14.
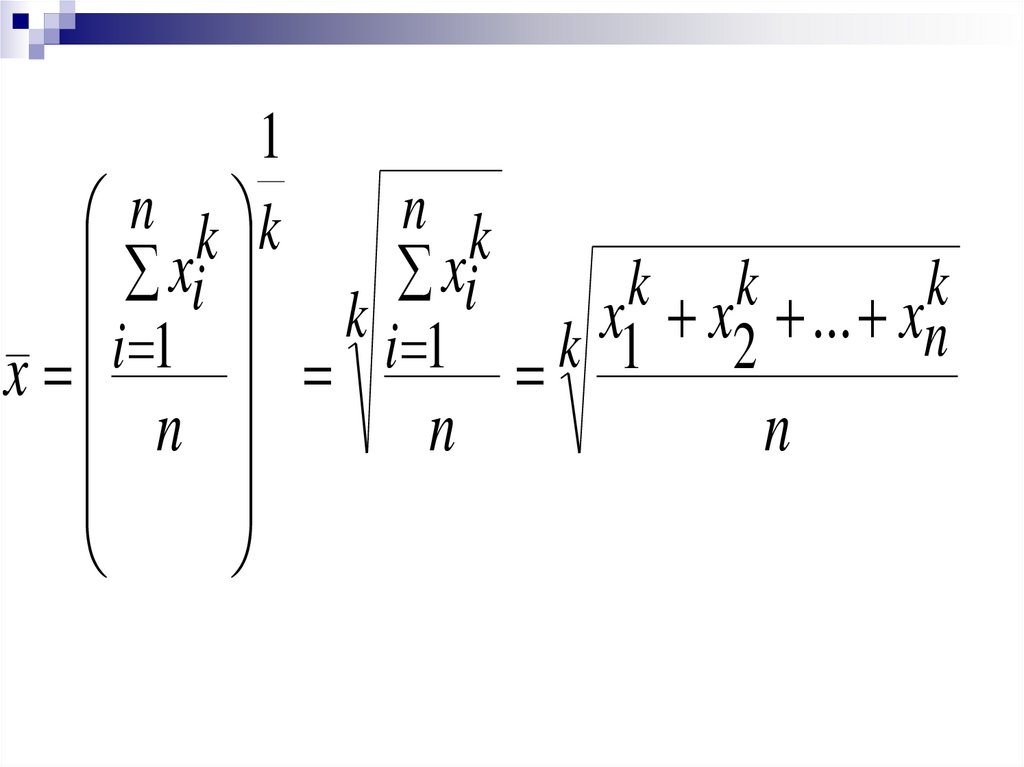
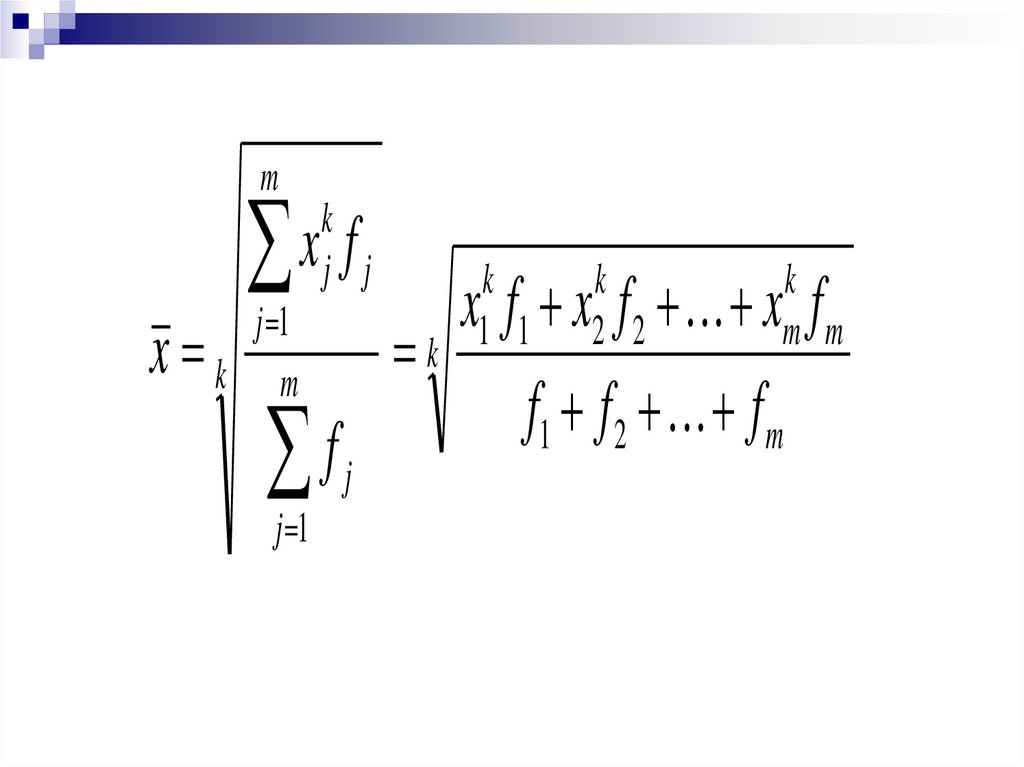
Перечисленные средниеобъединяются в общей формуле
степенной средней (при различной
величине k)
15.
1n k
n k k
xi
xi
k
k
k
k
x
x
...
x
n
k
i
1
i
1
1
2
x
n
n
n
16.
mx
x f
j 1
k m
k
j j
f
j 1
j
x f x f x f
k
f1 f 2 f m
k
1 1
k
2 2
k
m m
17.
Изменение показателя степени kприводит в каждом отдельном
случае к определенному виду
средней:
при k= -1 получается средняя
гармоническая
при k= 0 средняя геометрическая
при k= 1 средняя арифметическая
18.
при k= 2 средняя квадратическаяпри k= 3 средняя кубическая
при k= 4 средняя
биквадратическая
19.
Средняяарифметическая
при к= 1
20.
xарифм.n
n
xi
xi
1 i 1
i
1
n
n
21.
Торговыйцентр
1
2
3
4
5
6
Товарооборот
25
(млн.руб.)
18
27
32
15
21
22.
Определим средний размертоварооборота
23.
24.
25.
26.
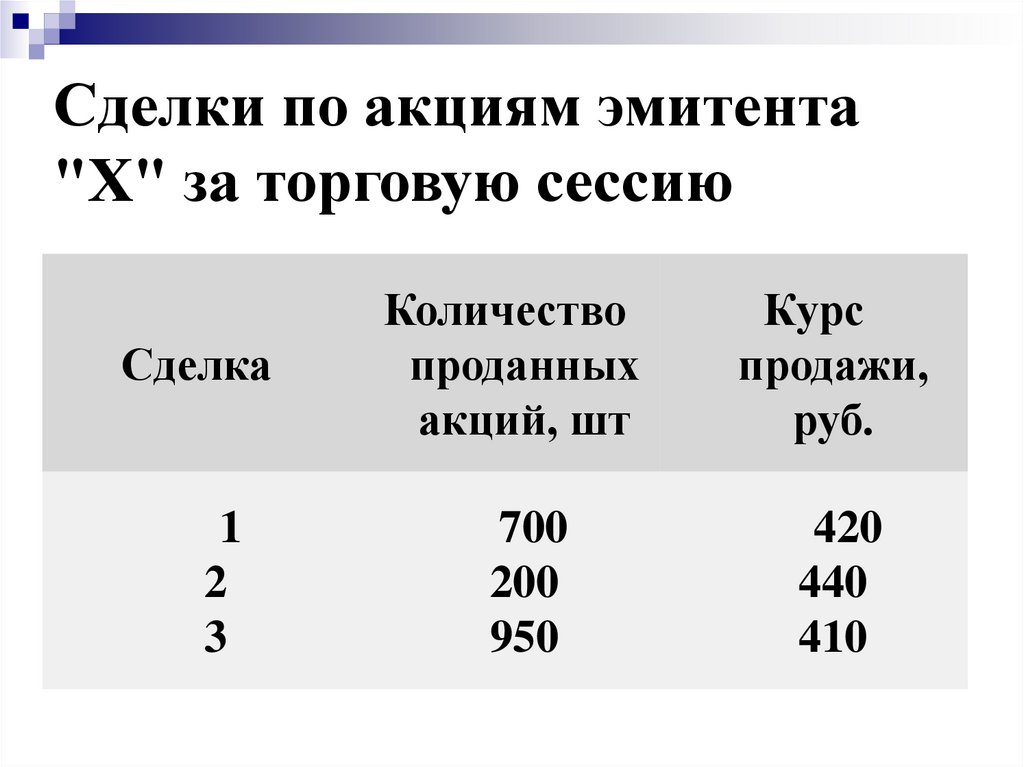
Сделки по акциям эмитента"Х" за торговую сессию
Сделка
Количество
проданных
акций, шт
Курс
продажи,
руб.
1
2
3
700
200
950
420
440
410
27.
Определим средний курспродажи акций
28.
29.
xfx
f
30.
31.
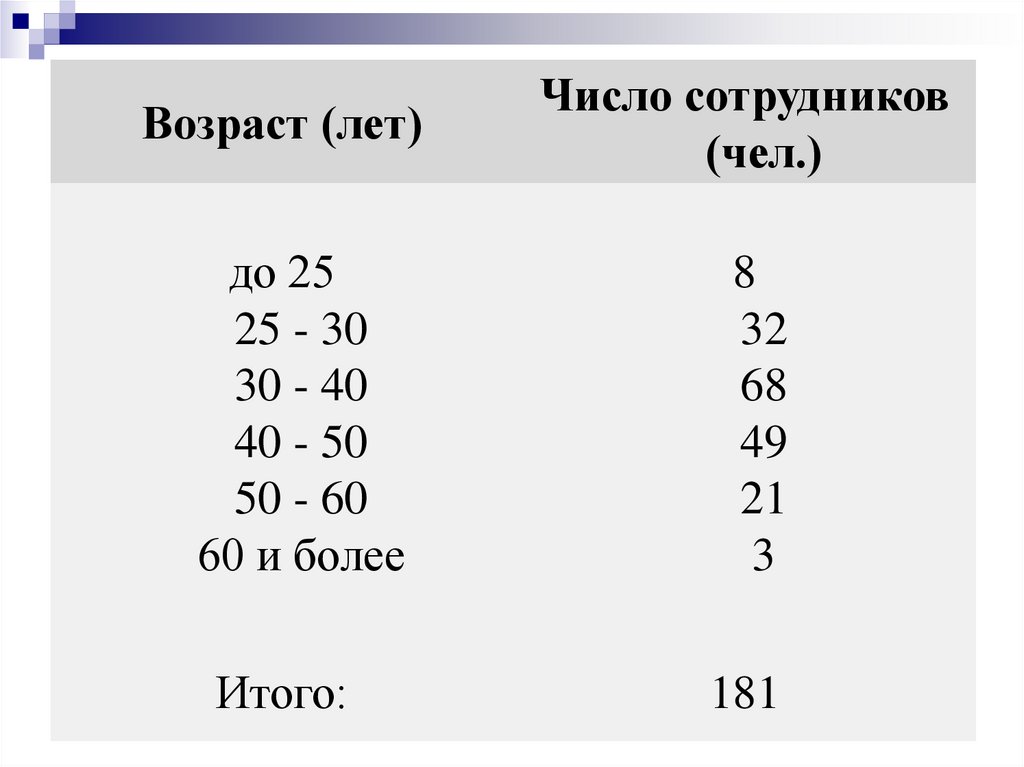
Возраст (лет)Число сотрудников
(чел.)
до 25
25 - 30
30 - 40
40 - 50
50 - 60
60 и более
8
32
68
49
21
3
Итого:
181
32.
1.ЗАКРОЕМ ОТКРЫТЫЕИНТЕРВАЛЫ
2.ОПРЕДЕЛИМ СЕРЕДИНЫ
ИНТЕРВАЛОВ
3. ПОСТАВИМ В
СООТВЕТСТВИЕ КАЖДОЙ
СЕРЕДИНЕ ИНТЕРВАЛА
ЧАСТОТУ ДАННОГО
ИНТЕРВАЛА
33.
22,5 27,5 35,0 45,0 55,0 65,08
32 68
49
21
3
34.
ИСС=35.
xfx
f
36.
37.
Средняягармоническая
при к= -1
38.
xn
1
x
39.
Mx
M
x
40.
Mi xi fi41.
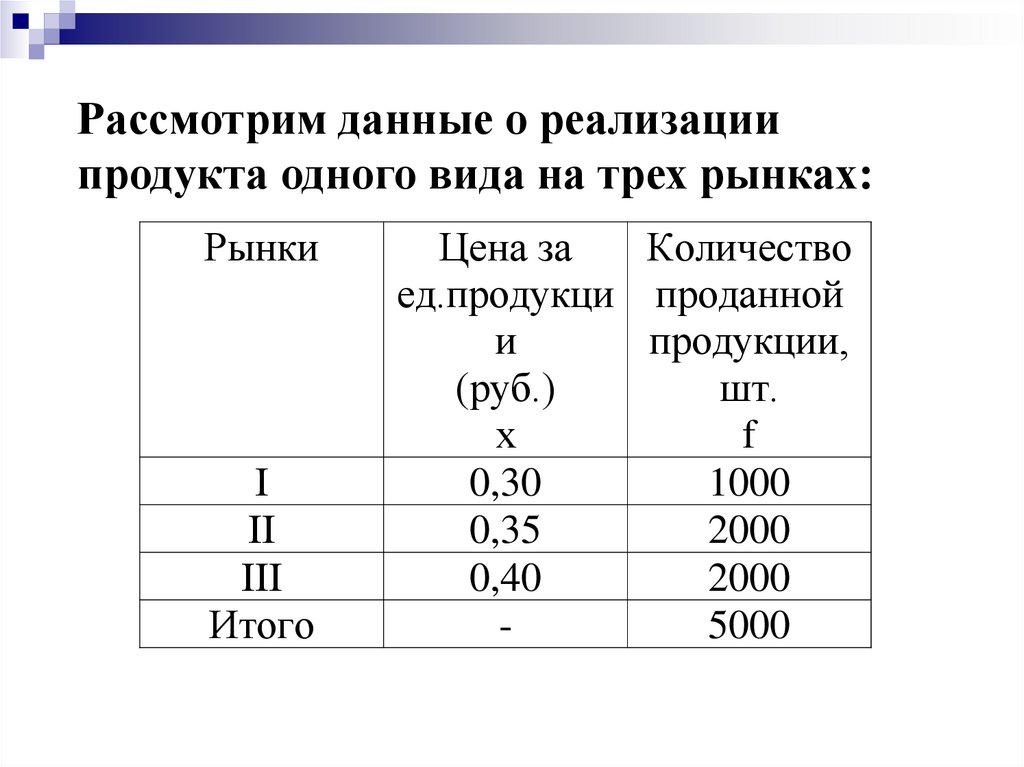
Рассмотрим данные о реализациипродукта одного вида на трех рынках:
Рынки
I
II
III
Итого
Количество
Цена за
ед.продукци проданной
продукции,
и
шт.
(руб.)
f
х
1000
0,30
2000
0,35
2000
0,40
5000
-
42.
ИСС=43.
0,30 1000 0,35 2000 0,4 2000x
0,36
1000 2000 2000
f
xf
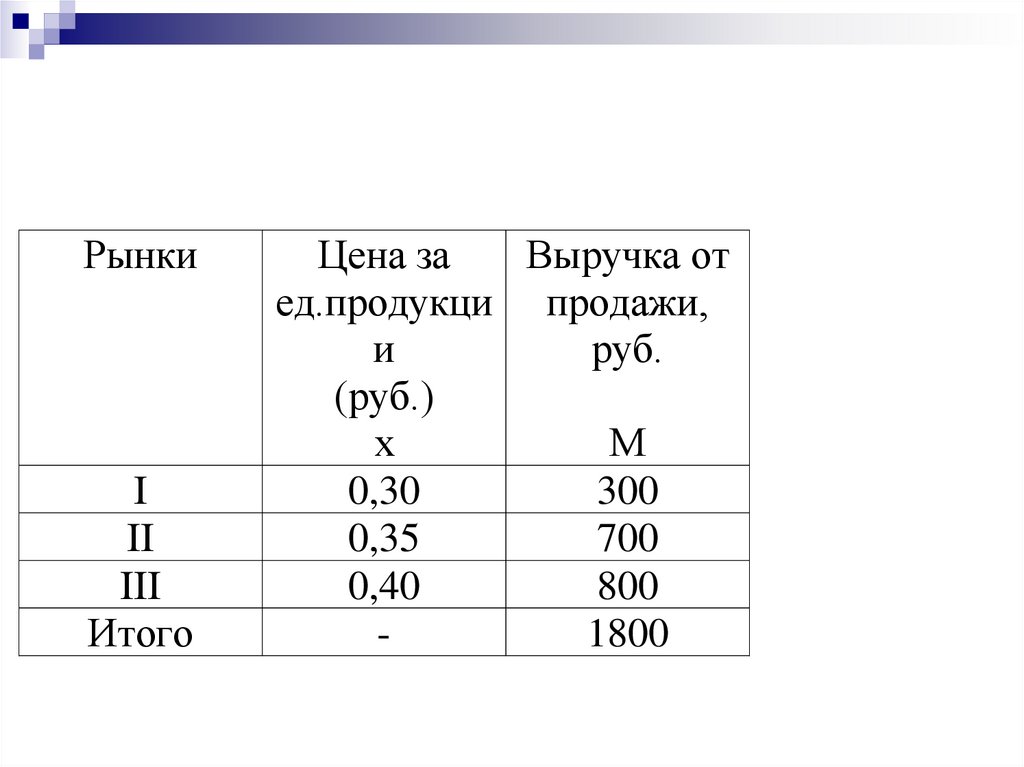
44.
РынкиI
II
III
Итого
Цена за
Выручка от
ед.продукци продажи,
и
руб.
(руб.)
х
М
0,30
300
0,35
700
0,40
800
1800
45.
ИСС=46.
300 700 800 1800x
0,36руб.
M 300 700 800 5000
x 0,3 0,35 0,4
M
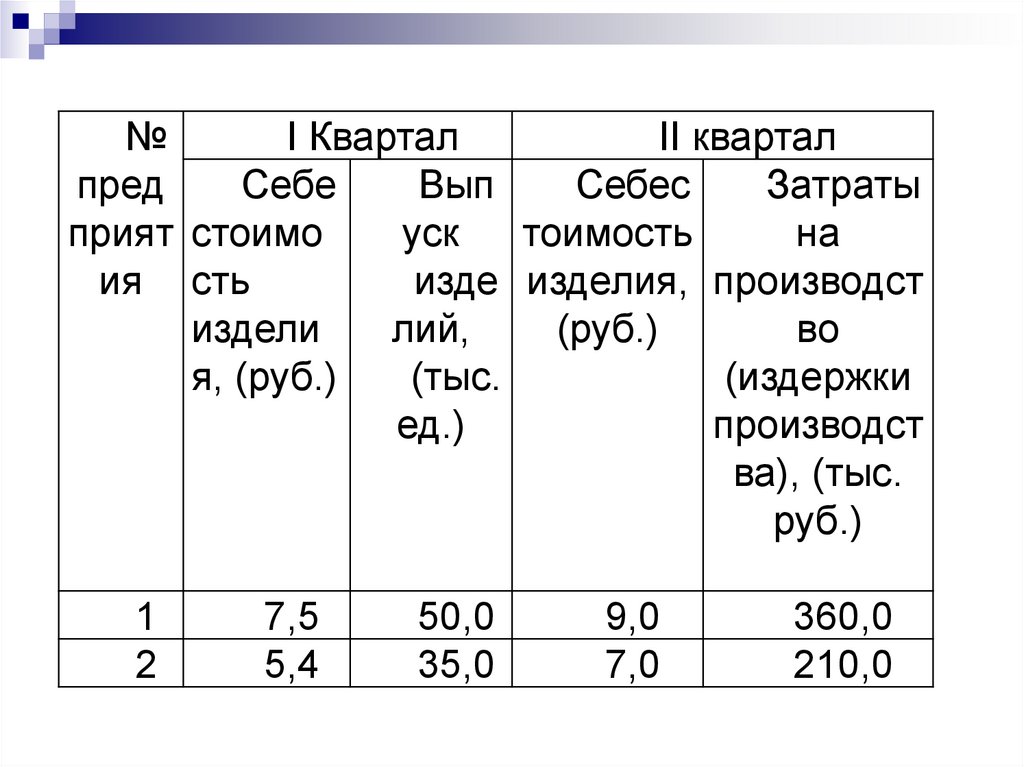
47.
I КварталII квартал
№
пред
Себе
Вып
Себес
Затраты
уск
прият стоимо
тоимость
на
ия сть
изде изделия, производст
лий,
(руб.)
издели
во
я, (руб.)
(тыс.
(издержки
ед.)
производст
ва), (тыс.
руб.)
1
2
7,5
5,4
50,0
35,0
9,0
7,0
360,0
210,0
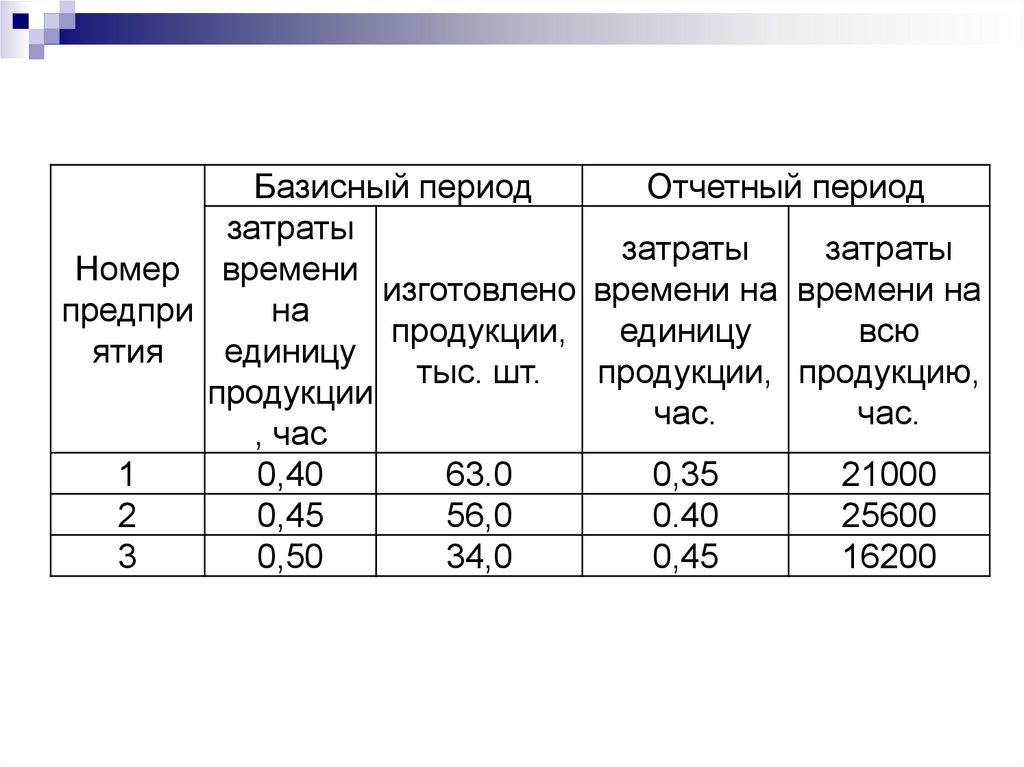
48.
Базисный периодОтчетный период
затраты
затраты
затраты
Номер времени
изготовлено времени на времени на
предпри
на
продукции,
единицу
всю
ятия
единицу
тыс. шт.
продукции, продукцию,
продукции
час.
час.
, час
1
0,40
63.0
0,35
21000
2
0,45
56,0
0.40
25600
3
0,50
34,0
0,45
16200
49.
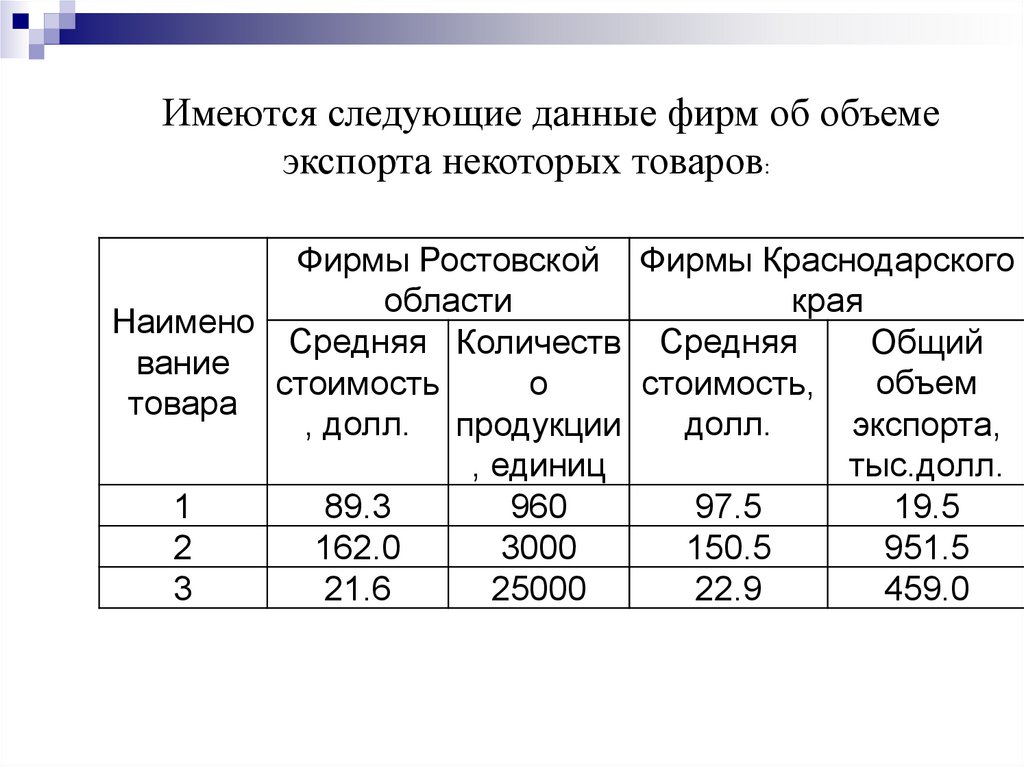
Имеются следующие данные фирм об объемеэкспорта некоторых товаров:
Фирмы Ростовской Фирмы Краснодарского
области
края
Наимено
Средняя Количеств Средняя
Общий
вание
объем
стоимость
о
стоимость,
товара
, долл. продукции
долл.
экспорта,
, единиц
тыс.долл.
1
89.3
960
97.5
19.5
2
162.0
3000
150.5
951.5
3
21.6
25000
22.9
459.0
50.
Вычислите среднюю стоимостьэкспортируемых
продовольственных товаров:
а) по фирмам Ростовской
области;
б) по фирмам Краснодарского
края.
Сравните данные. Укажите,
какие виды средних необходимо
применить.
51.
Средняя геометрическаяпри к = 0
52.
xгеом. n x1 x2 ... xn n xi53.
Пример. Максимальный выигрыш влотерее составляет миллион рублей, а
минимальный – сто рублей. Какую
величину можно считать средней между
миллионом и сотней? Арифметическая
средняя явно непригодна, так как
составляет 500050 рублей, а это, как и
миллион, крупный, а никак не средний
выигрыш. Геометрическая средняя в
этом случае дает наиболее правильный с
точки зрения экономики и логики ответ:
100 100000 10000
54.
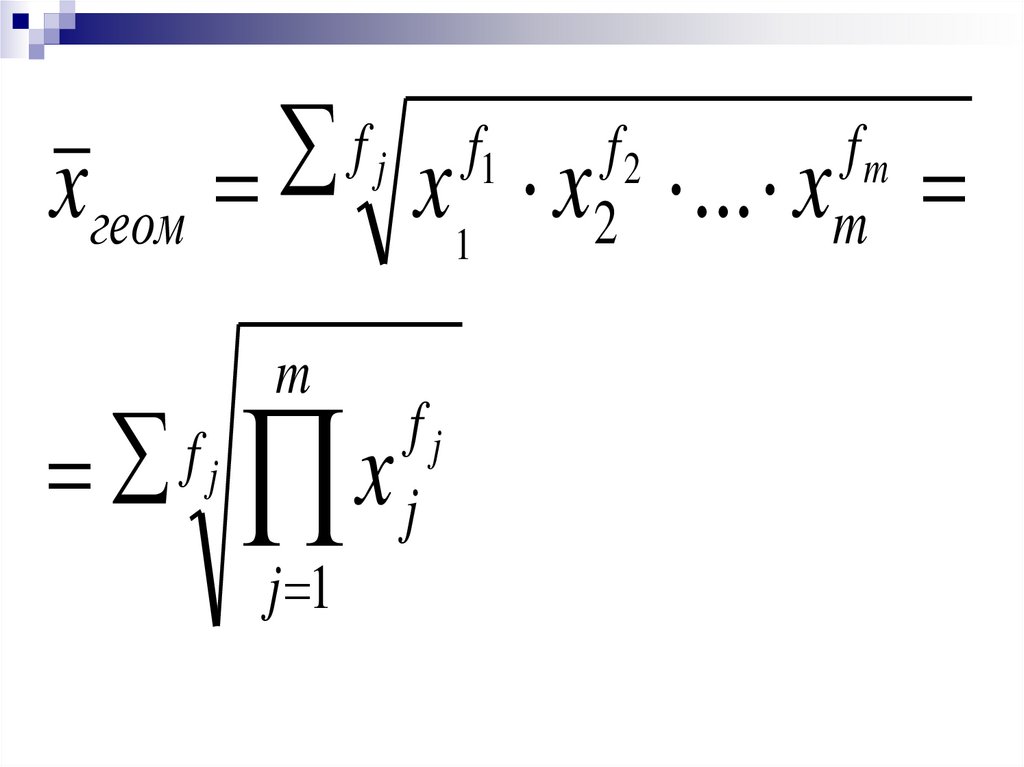
xгеомf j f1
fm
f2
x x ... x
1
m
f
j x
j 1
fj
j
2
m
55.
Средняя квадратическаяпри к = 2
56.
nxêâàäð.
x
i 1
n
2
i
57.
mx квадр
x
f
j
j 1
m
2
j
f
j
j 1
58.
Чем больше показатель степени,тем больше величина
соответствующей
средней (мажорантность
средних):
xгарм. xгеом. xарифм. xквадр.
59.
Структурные средние60.
При изучении статистическойсовокупности применяются
такие ее характеристики,
которые описывают
количественно структуру
совокупности, ее строение.
61.
Квантили – это варианты,занимающие определенное
место в ранжированной
совокупности.
62.
К квантилям относятся:перцентили, квартили,
децили и медиана,
63.
Медиана – это значениепризнака, относительно
которого совокупность
делится на две равные по
числу вариантов части.
64.
В зависимости отхарактера исходных
данных медиана
определяется по - разному
65.
Несгруппированные данные66.
Сгруппированные данные67.
0,5 fi vMe 1Ме xMe min k
f Me
68.
Мода – это значениепризнака, наиболее часто
встречающееся в
совокупности.
69.
В интервальномвариационном ряду мода
рассчитывается по
следующей формуле:
70.
f Mo f Mo 1Мо xMо min k
( f Mo f Mo 1 ) ( f Mo f Mo 1 )
71.
Среднююарифметическую,
медиану и моду часто
называют мерами
центральной тенденции.
72.
Средняя арифметическая имеетсущественные преимущества
перед другими мерами
центральной тенденции.
Средняя арифметическая
основывается на информации,
содержащей все значения ряда.
73.
Если средняяарифметическая близка к
моде и медиане, то она
типична.
74.
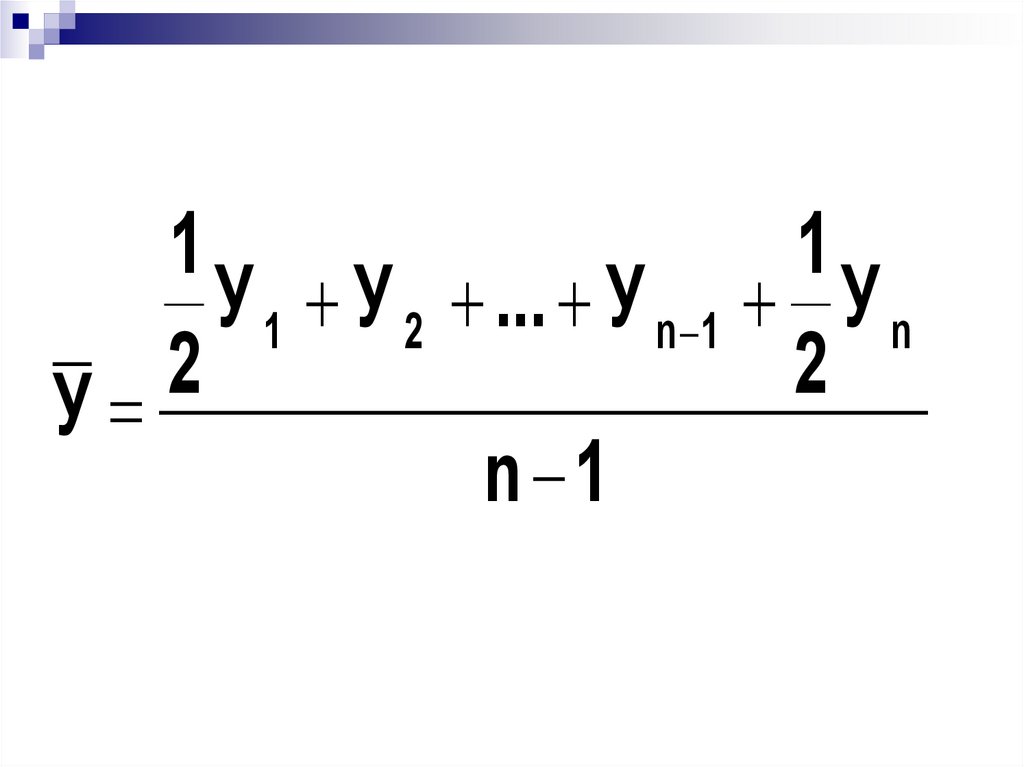
Прочие средние:Средняя хронологическая
простая
75.
11
У 1 У 2 ... У n 1 У n
2
2
У
n 1
76.
На фирме имеются следующие остаткиоборотных средств: на 1 января – 242 тыс.
руб.; на 1 февраля – 251 тыс. руб.; на 1
марта – 213 тыс. руб.; на 1 апреля – 186 тыс.
руб. Определить средний остаток оборотных
средств фирмы за первый квартал.
Решение:
В условии данные представлены в виде
моментного ряда с равностоящими датами,
средний уровень такого ряда определяется
по формуле:
77.
Решение:В условии данные представлены
в виде моментного ряда с
равностоящими датами, средний
уровень такого ряда определяется
по формуле средней
хронологической простой:
78.
242 / 2 251 213 186 / 2y
229 тыс.руб.
4 1

















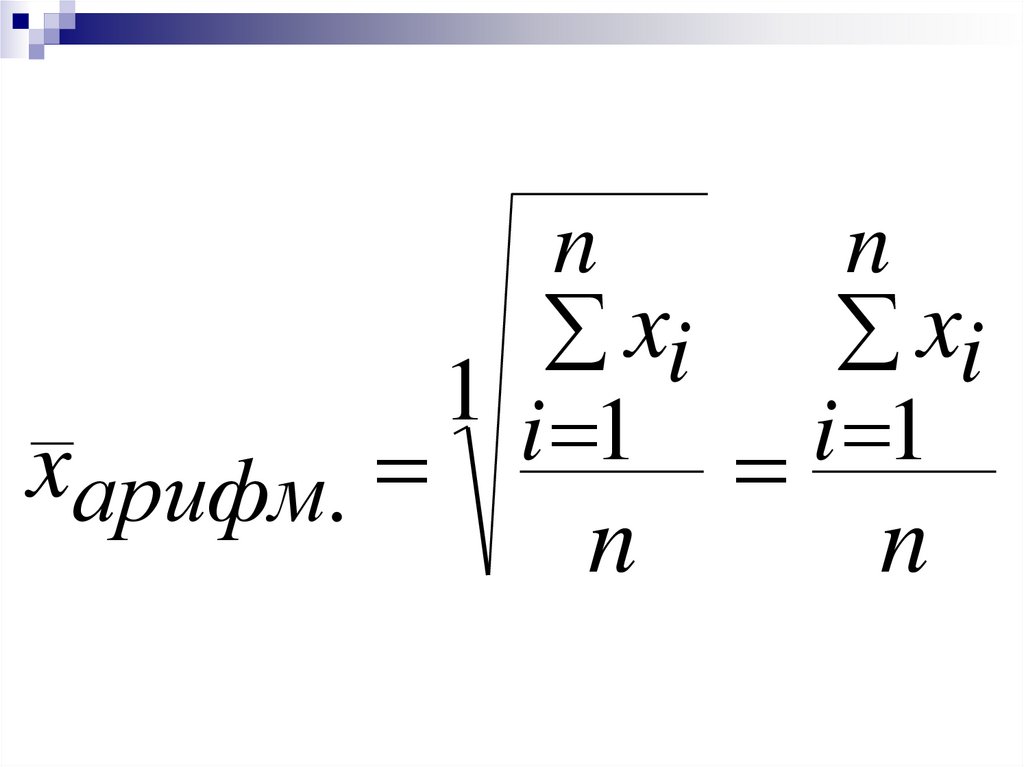



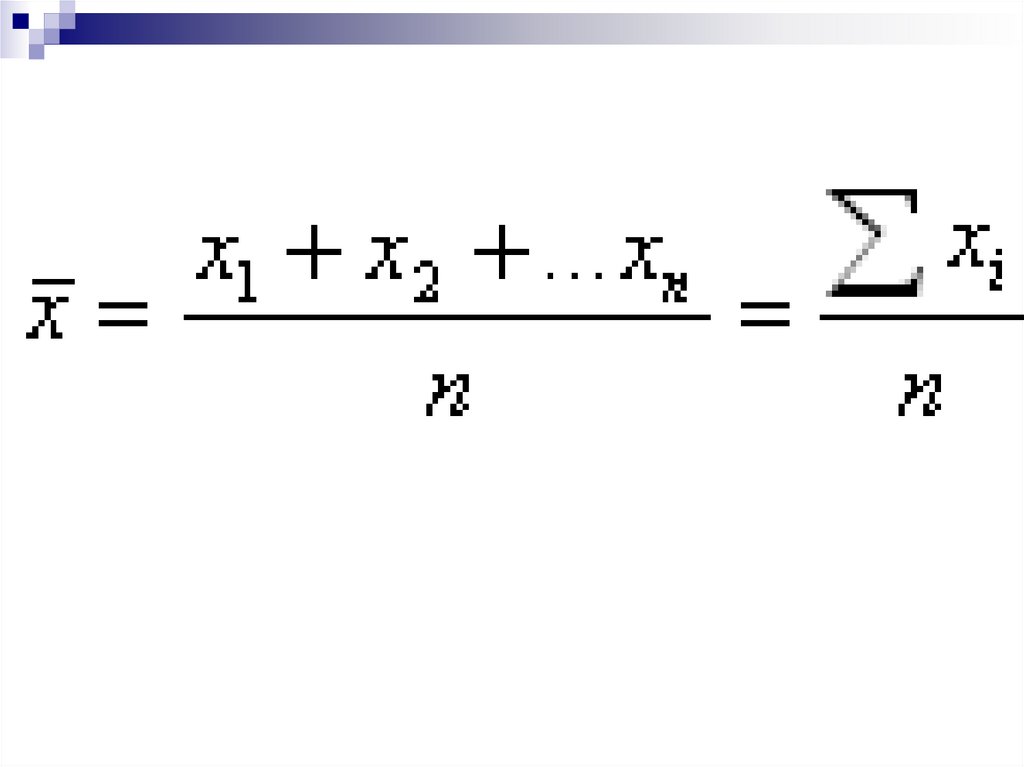
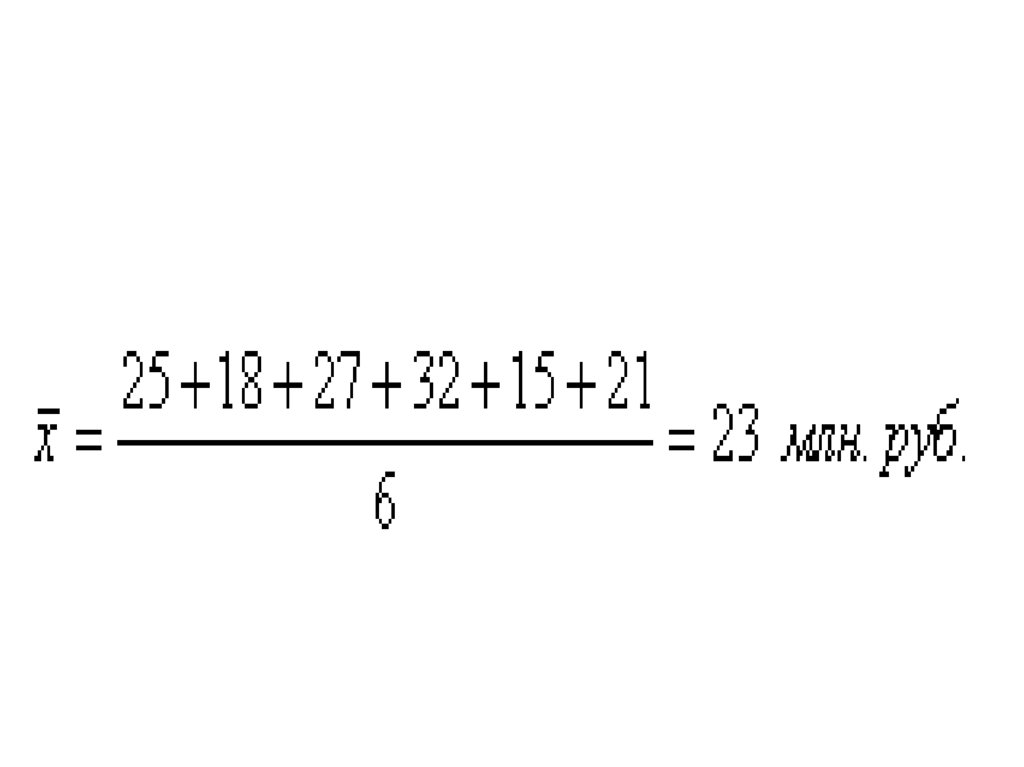


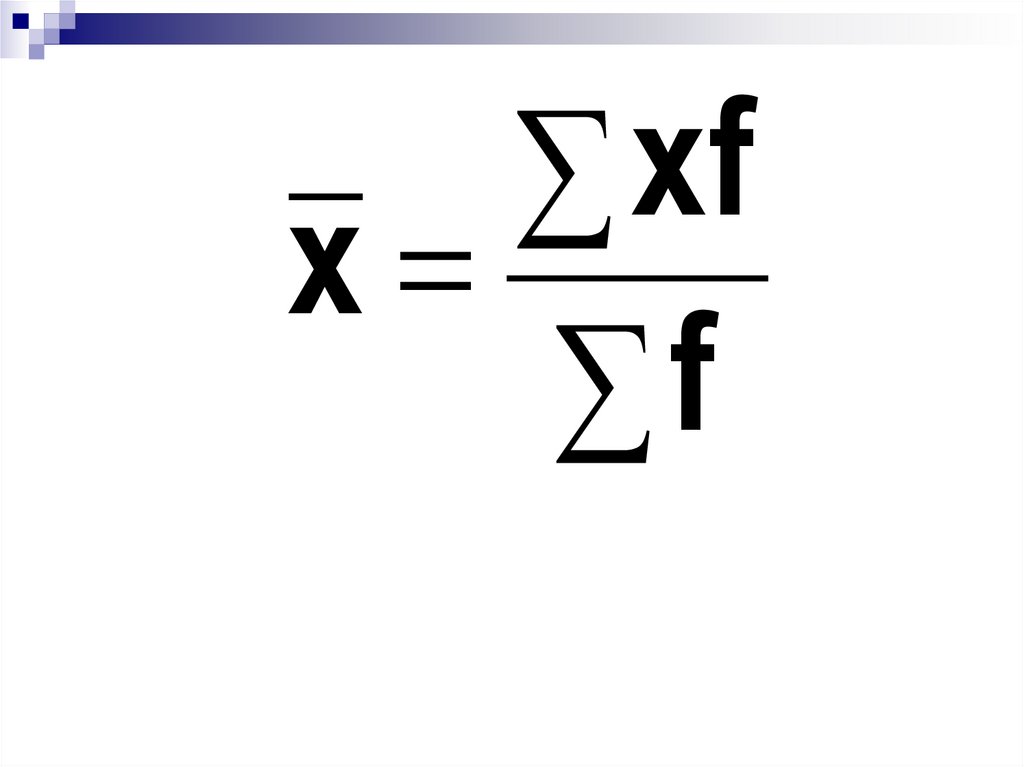



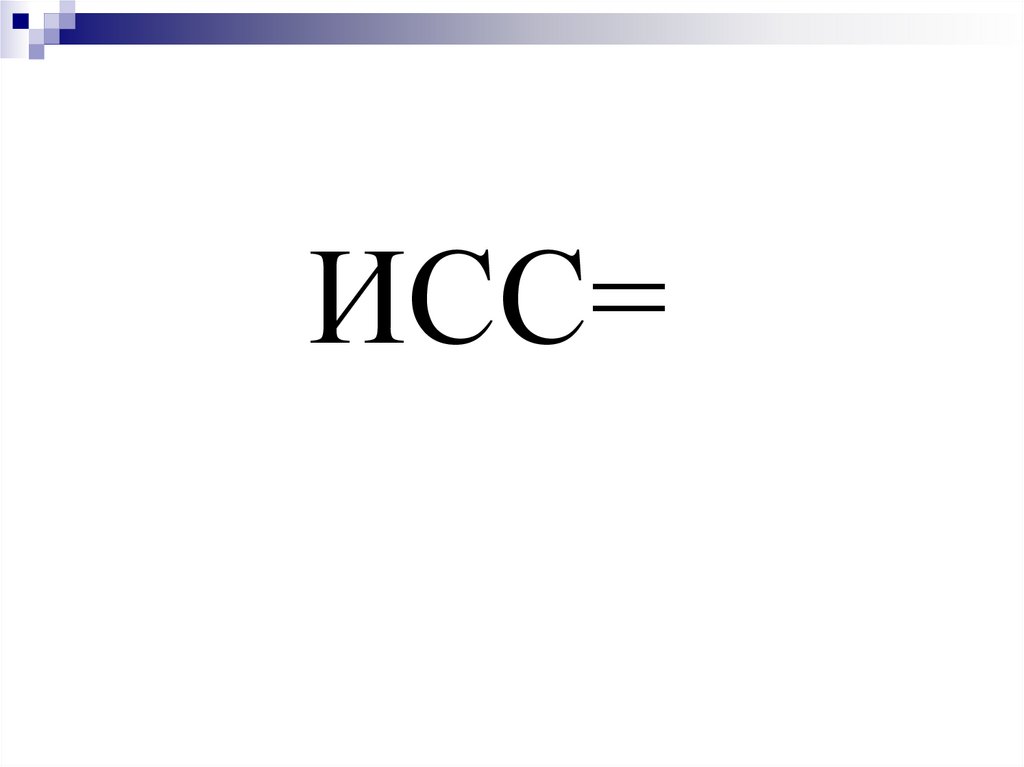
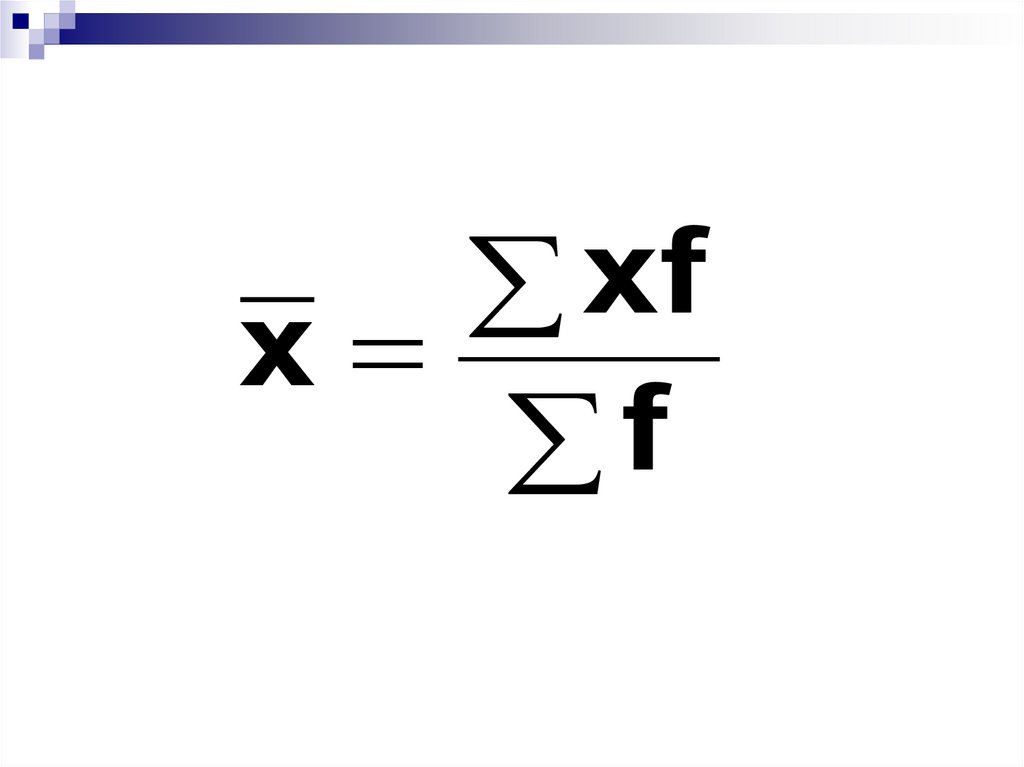
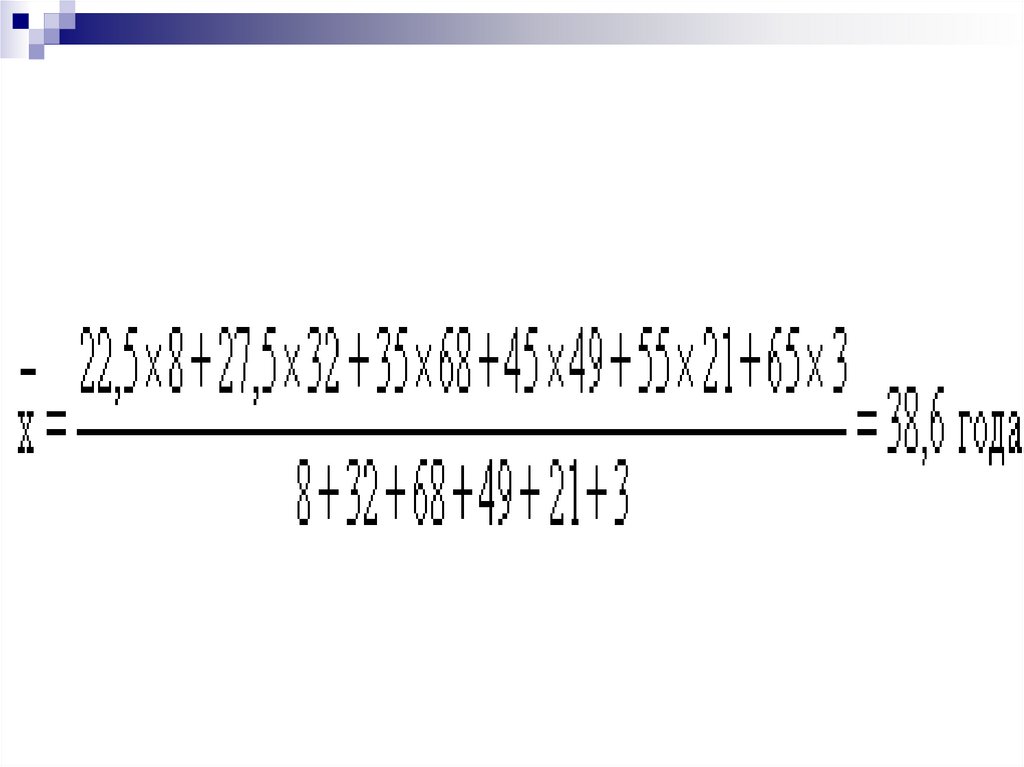

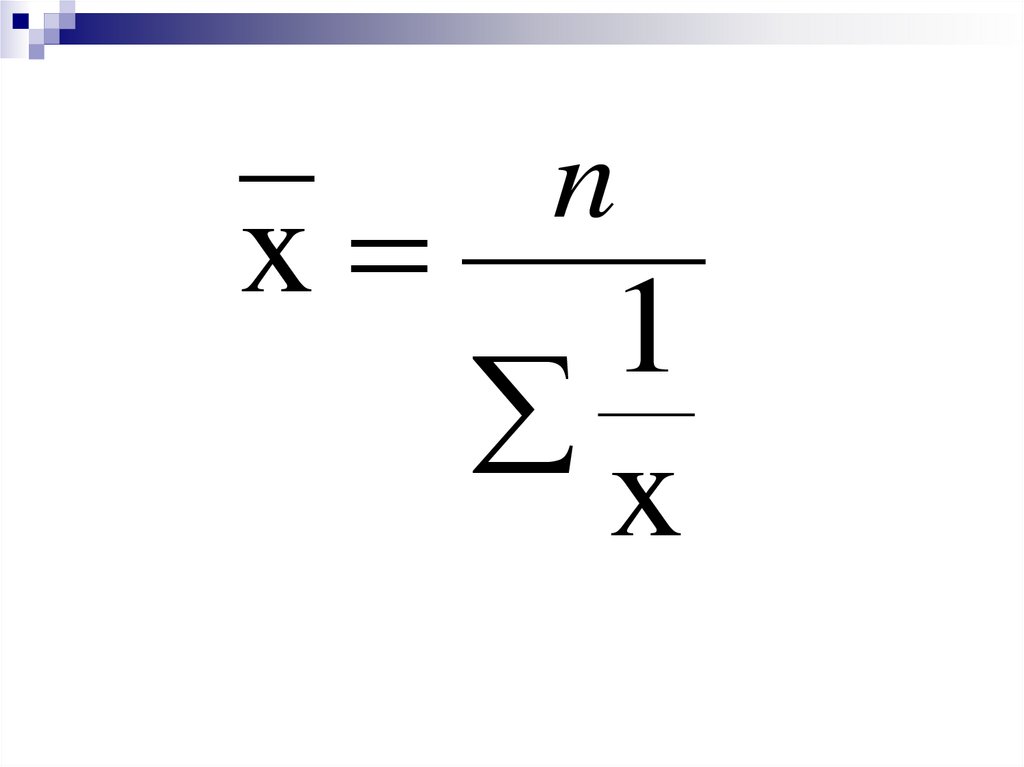
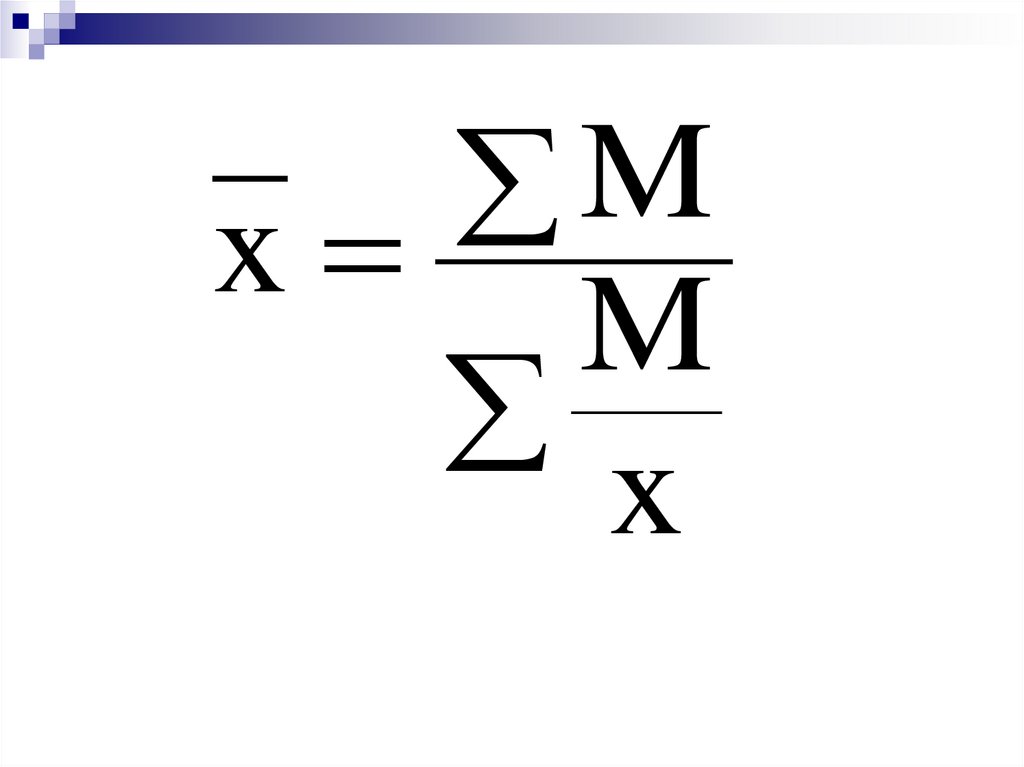
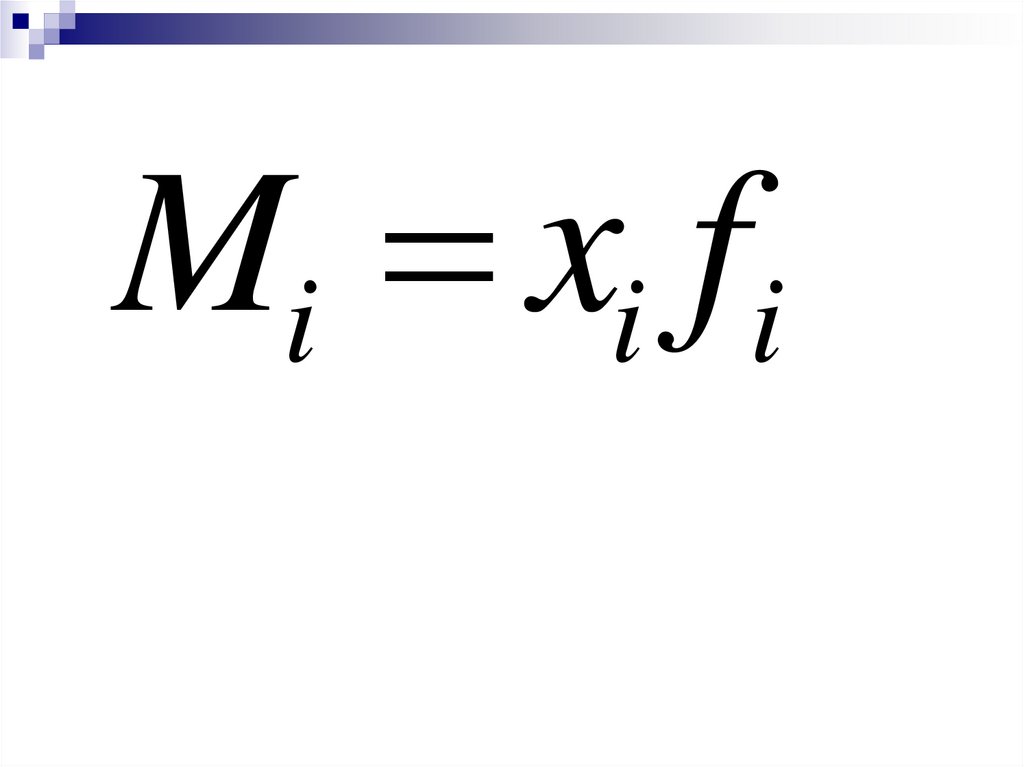
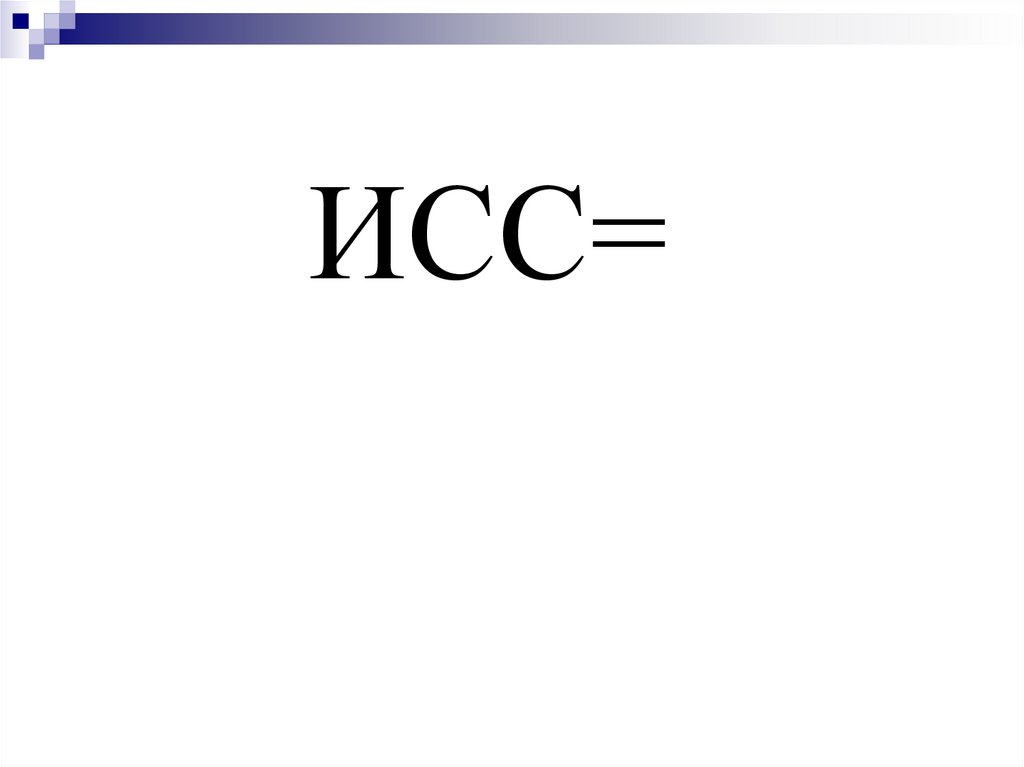

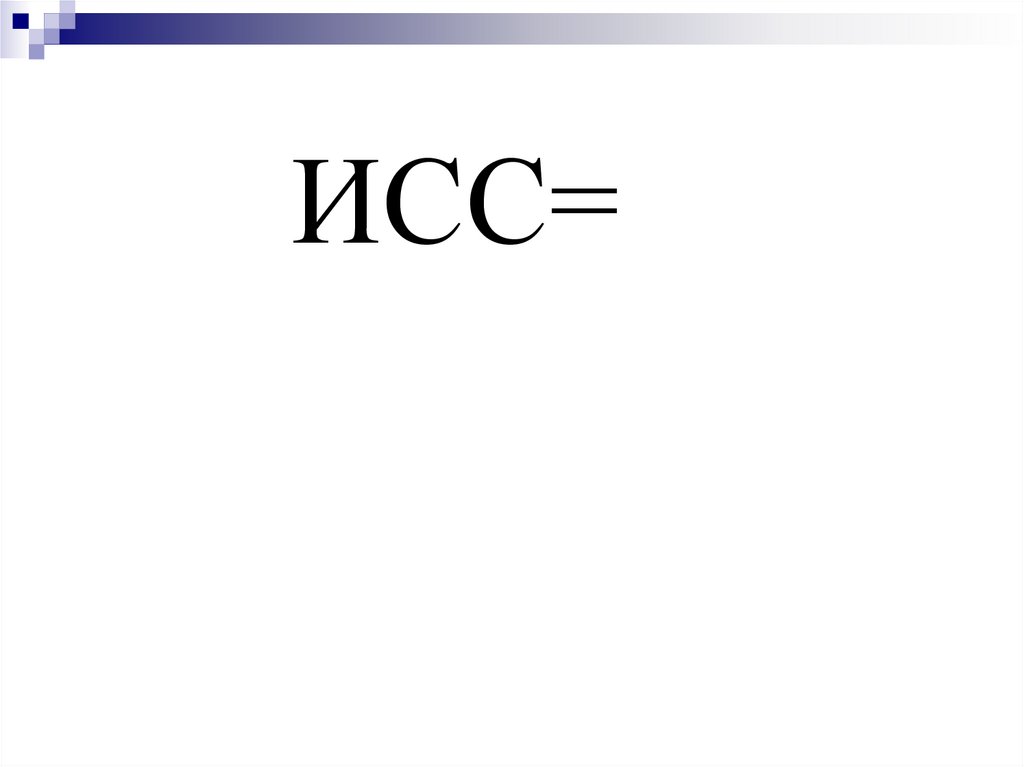



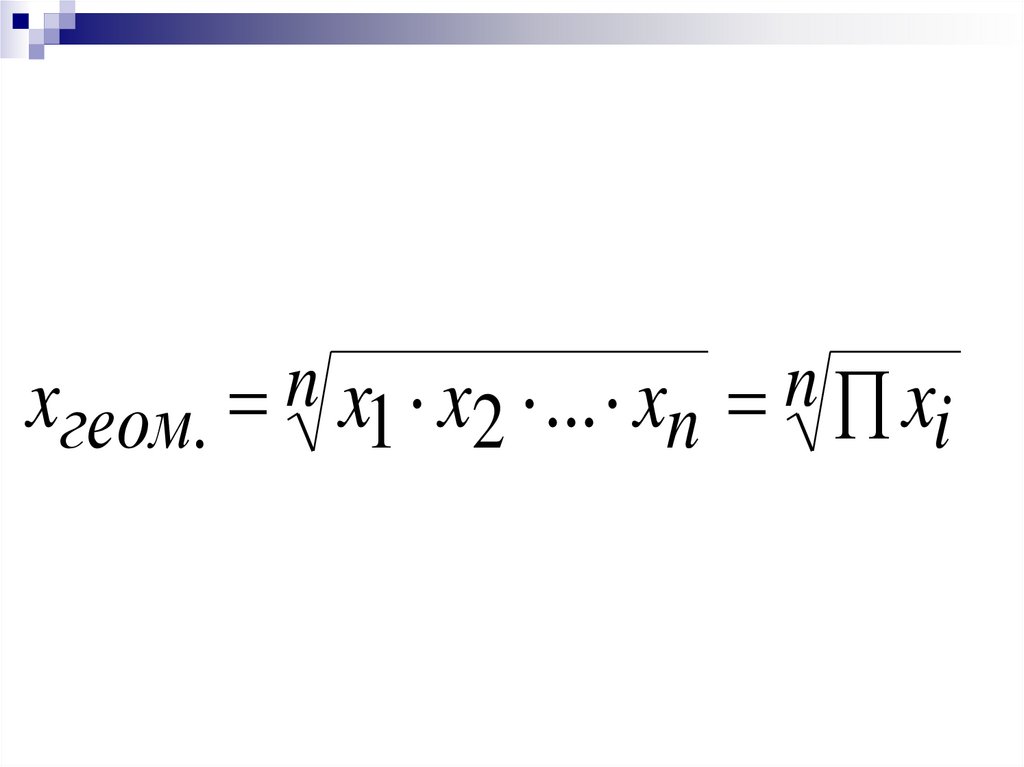


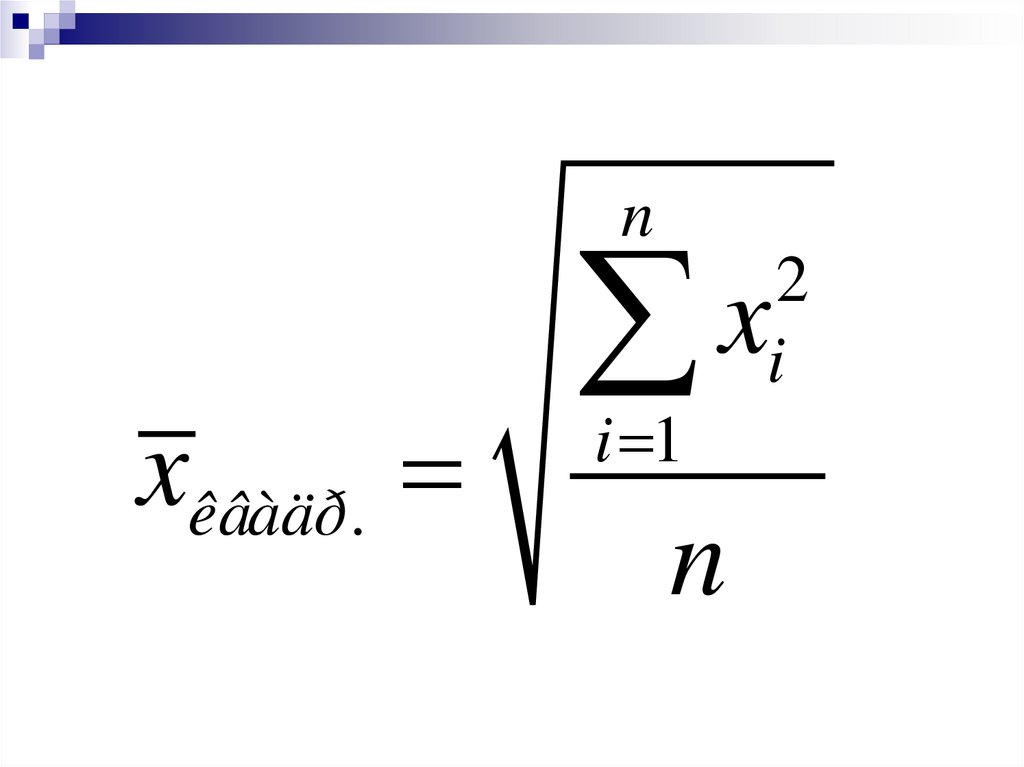
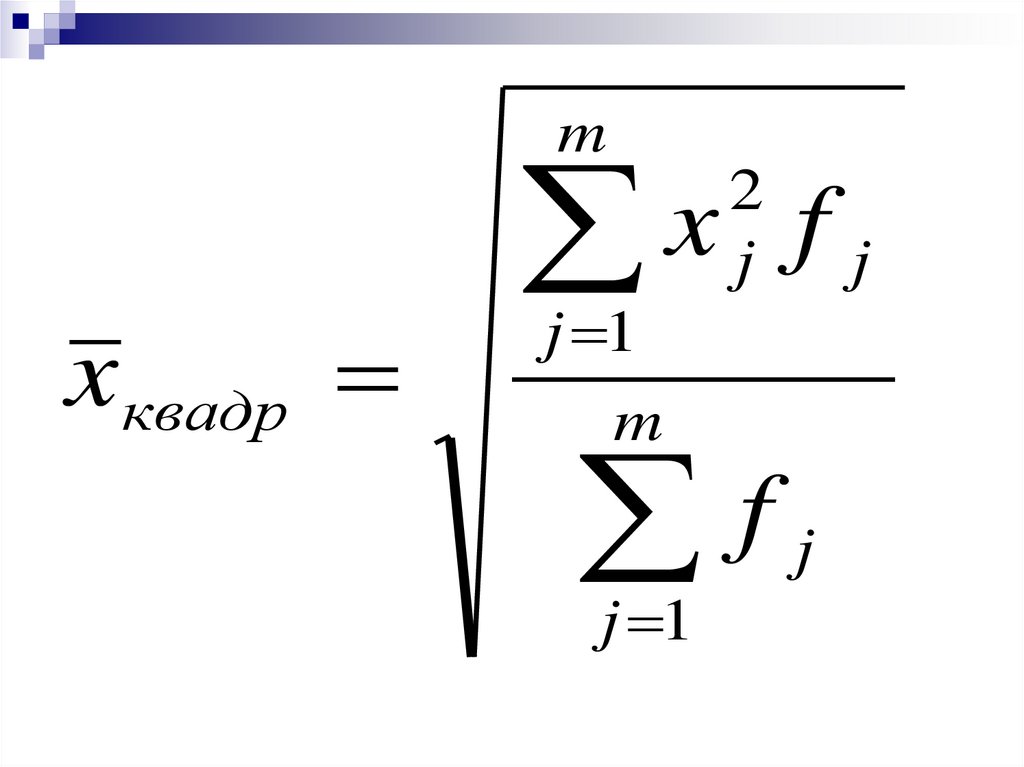









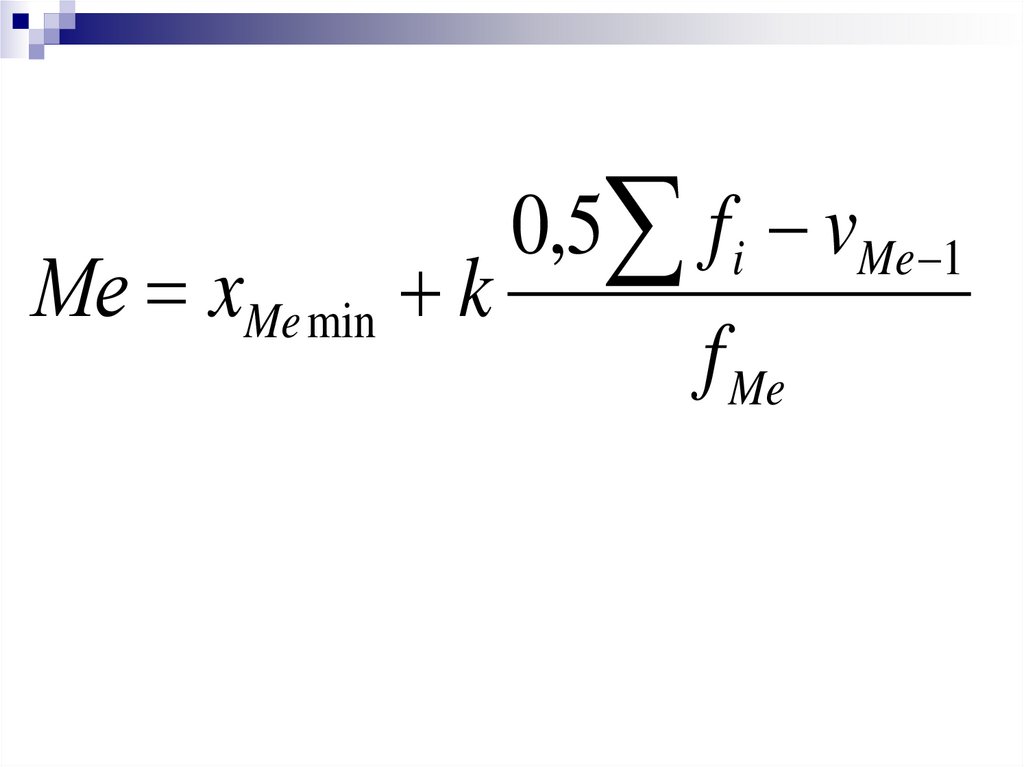










 mathematics
mathematics








