Similar presentations:
Средние показатели. Тема 5
1.
Средние показатели2.
Самый отдаленный пункт земного шарак чему-нибудь да близок, а самый близкий
от чего-нибудь да отдален
Козьма Прутков, Плоды раздумья
3.
План лекции1. Средняя, её сущность и
определение
2. Виды и формы средних величин
3. Средняя арифметическая
4. Средняя гармоническая
5. Средняя геометрическая
4.
В средней величине взаимопогашаютсяотклонения значений признака отдельных
единиц совокупности, обусловленные
действием случайных факторов, и
проявляются изменения, вызванные
действием основных факторов. Это
позволяет средней отражать типичный
уровень признака и абстрагироваться от
индивидуальных особенностей, присущих
отдельным единицам
5.
Взаимодействие элементовсовокупности приводит к
ограничению вариации хотя
бы части их свойств.
6.
Главное значение среднихвеличин состоит в их
обобщающей функции, то
есть замене индивидуальных значений признака
средней величиной,
характеризующей всю
совокупность явлений.
7.
Если средняя величинаобобщает качественно
однородные значения
признака, то она является
типической
характеристикой признака в
данной совокупности
8.
Системные средние -характеристики государства
как единой экономической
системы
9.
Метод средних не ограничиваетсятолько расчетом средней
арифметической, существуют и
другие виды средних.
10.
Определить среднюю можно черезисходное соотношение средней (ИСС)
или ее логическую формулу:
ИСС=(Суммарное значение или объем
осредняемого признака)/(число единиц
или объем совокупности)
11.
Для каждого показателя, используемогов экономическом анализе, можно
составить только одно истинное
исходное соотношение для расчета
средней.
12.
Для расчета средней заработной платыработников предприятия необходимо общий
фонд заработной платы разделить на число
работников:
13.
14.
15.
От того, в каком виде представленыисходные
данные
для
расчета
средней, зависит, каким именно
образом
будет
реализовано
ее
исходное соотношение. В каждом
конкретном случае для реализации
исходного соотношения потребуется
одна из следующих форм средней
величины:
16.
средняя арифметическая;средняя гармоническая;
средняя геометрическая;
средняя квадратическая,
кубическая и т.д.
17.
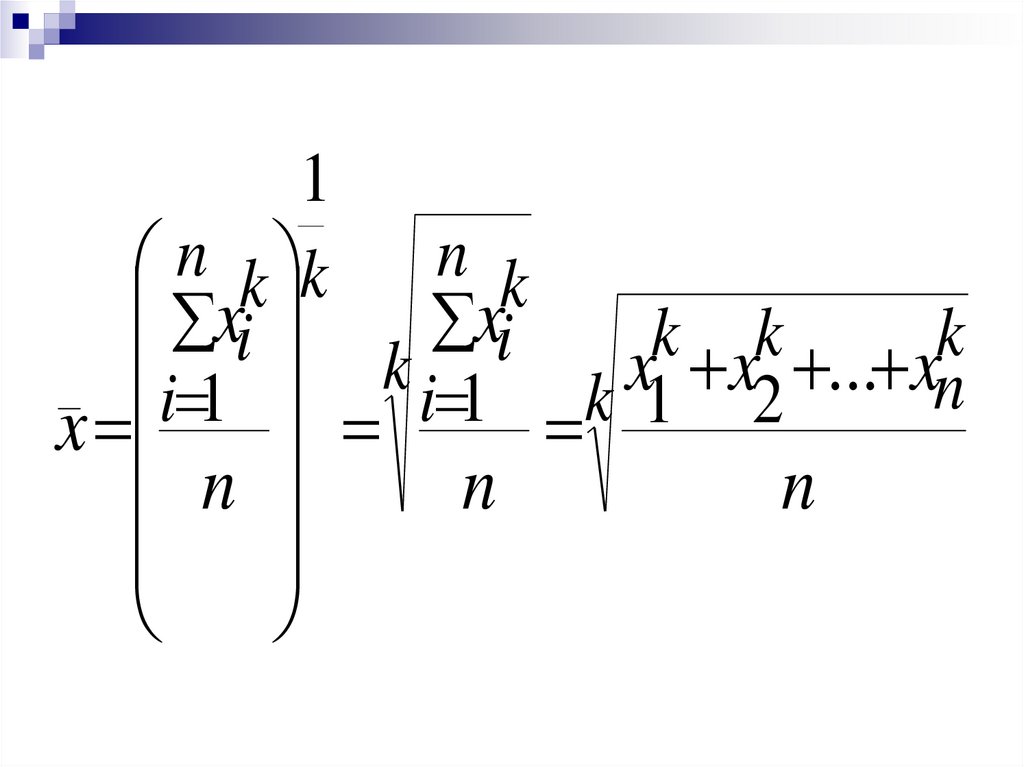
Перечисленные средниеобъединяются в общей формуле
степенной средней (при различной
величине k)
18.
1n k
n k k
xi
xi
k
k
k
k
x
x
...
x
n
k
i
1
i
1
1
2
x
n
n
n
19.
1n k k n k
xi
xi
k
k
k
k
x
x
...
x
n
k
i
1
i
1
1
2
x
n
n
n
20.
Изменение показателя степени kприводит в каждом отдельном
случае к определенному виду
средней
21.
11
n 1
xi
i
1
xгарм.
n
n 1
xi
1 i 1
n
n 1
n
x
i 1 i
22.
11
n 1
xi
i
1
xгарм.
n
n 1
xi
1 i 1
n
n 1
n
x
i 1 i
23.
xгеом. n x1 x2 ... xn n xi24.
nn
xгеом. x1 x2 ... xn xi
25.
xарифм.n
n
xi
xi
1 i 1
i
1
n
n
26.
xарифм.n
n
xi
xi
1 i 1
i
1
n
n
27.
nxêâàäð.
x
i 1
n
2
i
28.
nxêâàäð.
x
i 1
n
2
i
29.
Поскольку вариационные ряды обычносгруппированы по одинаковым значениям
признака, либо в интервалах его значений,
то чаще для расчетов применяют формулы
средних взвешенных. В этих формулах в
качестве весов выступают значения частот.
30.
nxгарм.
xгеом.
f
i 1
i
n
1
fi
i 1 xi
f i f1
f2
fi
x x ... ..
1
2
x
i
fi
31.
nxарифм.
x f
i 1
n
i
f
i 1
i
i
n
xкв адр.
x f
i 1
n
2
i
f
i 1
i
i
32.
Во всех формулах xi –индивидуальныезначения признака; fi – частота
повторения индивидуального значения
признака, n – объем совокупности.
33.
Чем больше показатель степени,тем больше величина
соответствующей
средней (мажорантность
средних):
xгарм. xгеом. xарифм. xквадр.
34.
xгарм. xгеом. xарифм. xквадр.35.
Торговоепредприятие
1
2
3
4
5
6
Товарооборот
25
(млн.руб.)
18
27
32
15
21
36.
37.
38. Сделки по акциям эмитента "Х" за торговую сессию
Сделки по акциям эмитента "Х" заторговую сессию
Сделка
Количество
проданных
акций, шт
Курс
продажи,
руб.
1
2
3
700
200
950
420
440
410
39.
40.
41.
В отдельных случаях веса могут бытьпредставлены не абсолютными величинами,
а относительными (в процентах или долях
единицы). Так, в приведенном выше примере
количество проданных в ходе каждой сделки
акций соответственно составляет 37,8%
(0,378); 10,8% (0,108) и 51,4% (0,514) от их
общего числа. Тогда, с учетом несложного
преобразования
формулы
взвешенной
средней арифметической получим:
42.
= 420 · 0,378 + 440 · 0,108 + 410 · 0,514 = 417,03 руб.43.
Часто встречаемая при расчете среднихошибка заключается в игнорировании весов в
тех случаях, когда эти веса в действительности
необходимы.
Предположим,
имеются
следующие данные:
Себестоимость продукции "Z"
Предприятие
1
2
Себестоимость единицы
продукции, руб.
37
39
44.
Можно ли по имеющимся данным определитьсреднюю себестоимость данной продукции по двум
предприятиям, вместе взятым? Можно, но только в
том случае, когда объемы производства данной
продукции на двух предприятиях совпадают. Тогда
средняя
себестоимость
составит
38,0
руб.
(доказательство этого правила будет приведено
ниже.). Однако на первом предприятии за
рассматриваемый период может быть произведено, к
примеру, 50 единиц продукции, а на втором - 700
единиц. Тогда для расчета средней себестоимости
потребуется
уже
средняя
арифметическая
взвешенная:
45.
Использовать среднюю арифметическуюневзвешенную можно только тогда, когда
точно установлено отсутствие весов или их
равенство.
46.
При расчете средней поинтервальному вариационному
ряду для выполнения необходимых
вычислений от интервалов переходят
к их серединам.
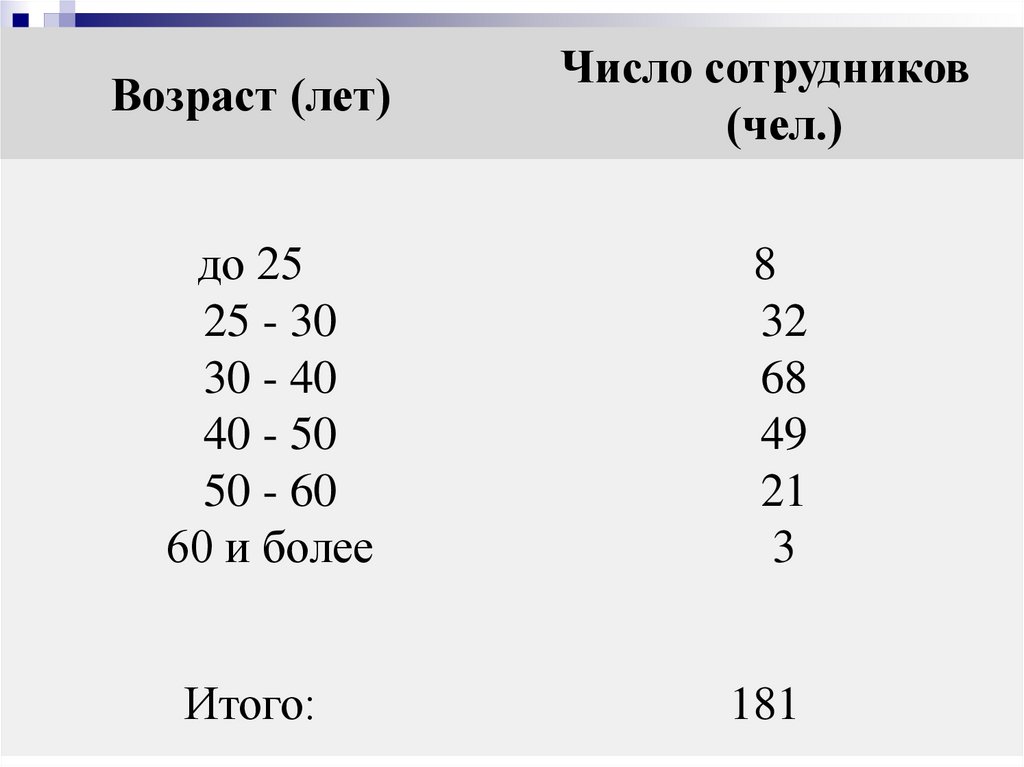
47.
Возраст (лет)Число сотрудников
(чел.)
до 25
25 - 30
30 - 40
40 - 50
50 - 60
60 и более
8
32
68
49
21
3
Итого:
181
48.
Для определения среднего возрастаперсонала найдем середины возрастных
интервалов. При этом величины открытых
интервалов (первого и последнего) условно
приравниваются к величинам интервалов,
примыкающих к ним (второго и
предпоследнего). С учетом этого середины
интервалов будут следующими:
22,5 27,5 35,0 45,0 55,0 65,0
49.
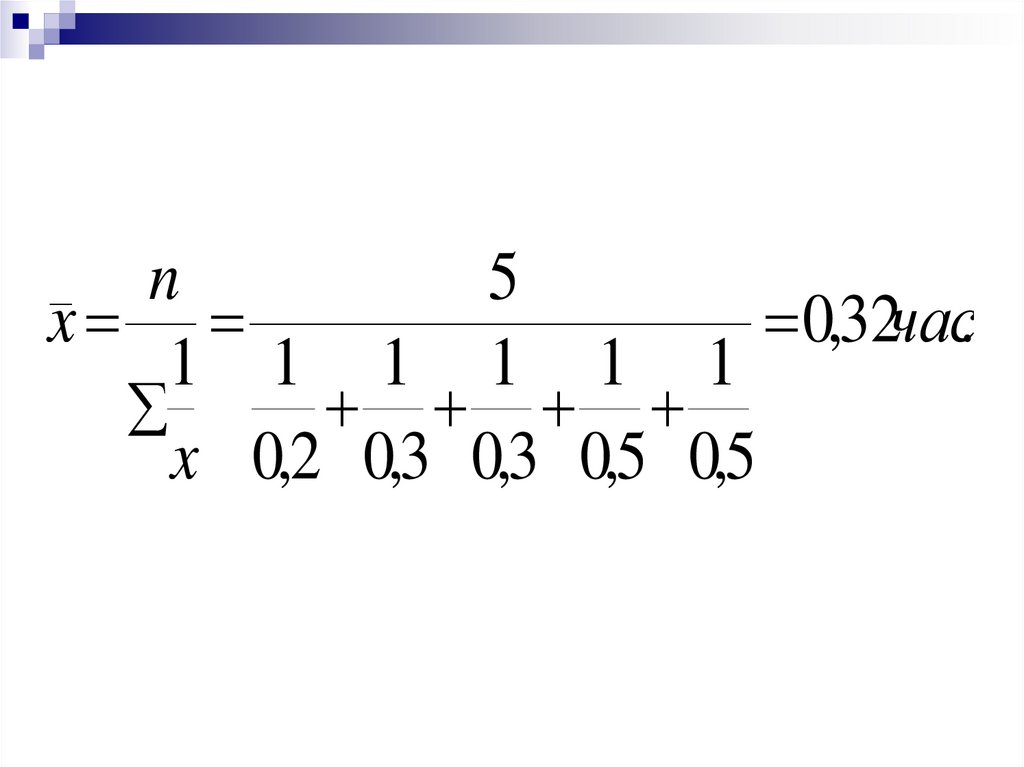
Средняя гармоническаяВремя на изготовление одной
детали (x) в часах:
0,2; 0,3; 0,3; 0,5; 0,5
Требуется рассчитать среднее
время, затрачиваемое одним
рабочим на изготовление детали.
50.
51.
Для решения необходимы данныеоб общих затратах времени всех
пяти рабочих и о числе
выработанных за это время
деталей.
Исходим из предположения, что
рабочие работали один час. Тогда
общие затраты времени составят 5
человеко-часов.
52.
За это время первый рабочийвыработает 1/0,2=5 деталей,
второй и третий по 1/0,3=3,3
детали, а четвертый и пятый по
1/0,5=2 детали. Все вместе они
выработали 15,6 деталей.
53.
В среднем на одну детальзатрачивалось 5/15,6=0,32
часа.
Если все расчеты представить
в виде формулы, то
последняя и будет
представлять собой среднюю
гармоническую простую:
54.
n5
x
0,32час.
1 1 1 1 1 1
x 0,2 0,3 0,3 0,5 0,5
55.
n5
x
0,32час.
1 1 1 1 1 1
x 0,2 0,3 0,3 0,5 0,5
56.
В целом ряде случаевприменение средней
арифметической или средней
гармонической определяется
лишь наличием исходных
данных.
57.
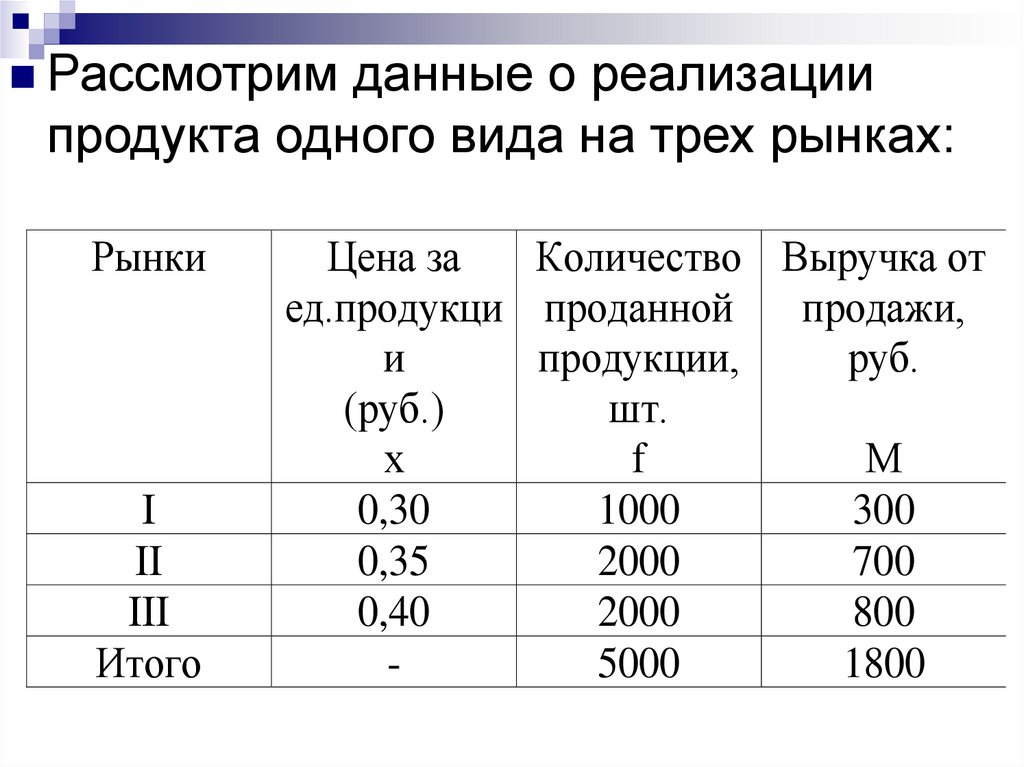
Рассмотрим данные о реализациипродукта одного вида на трех рынках:
Рынки
I
II
III
Итого
Цена за
Количество Выручка от
ед.продукци проданной
продажи,
и
продукции,
руб.
(руб.)
шт.
х
f
М
0,30
1000
300
0,35
2000
700
0,40
2000
800
5000
1800
58.
Требуется рассчитать среднюю цену, покоторой продавался товар.
1) Предположим, мы располагаем только
данными о ценах на трех рынках и о
количестве товара, проданного на каждом
их них. При этом цены на отдельных
рынках выступают в качестве вариантов, а
количество проданного товара – в
качестве весов. Тогда средняя цена
определится
по
по
средней
арифметической взвешенной
59.
0,30 1000 0,35 2000 0,4 2000x
0,36
1000 2000 2000
f
xf
60.
0,30 1000 0,35 2000 0,4 2000x
0,36
1000 2000 2000
f
xf
61.
Теперь предположим, что количествопроданного товара неизвестно, а известны
лишь цены и выручка от продажи.
62.
M i xi f iM
fi
xi
63.
Mi xi fiM
fi
xi
64.
M M 1 M 2 ... M mx гар.
M M1 M 2
Mm
...
x x1 x2
xm
65.
M M1 M2 ... Mmxгар.
M M1 M2
Mm
...
x x1 x2
xm
66.
300 700 800 1800x
0,36 руб.
M 300 700 800 5000
x 0,3 0,35 0,4
M
67.
300 700 800 1800x
0,36руб.
M 300 700 800 5000
x 0,3 0,35 0,4
M
68.
В результате проверки двух партий мукипотребителям установлено, что в
первой партии муки высшего сорта
было 3942 кг., что составляет 70,4%
общего веса муки этой партии. Во
второй партии муки высшего сорта
было 6520 кг., что составляет 78,6%
общего веса муки этой партии.
Определите процент муки высшего
сорта в среднем по первой и второй
партиям вместе
69.
70.
Средняя геометрическаяПредположим, Вы внесли деньги в банк на
срочный депозит, процент по которому ежегодно
изменяется
в
зависимости
от
ставки
рефинансирования ЦБ.
После каждого года сумма, равная процентному
приросту, добавляется к сумме счета.
Например, первоначальная сумма вклада
составила 100 денежных единиц. За первый Вы
получили 5% дохода по вкладу, за второй 7%, за
третий 9% и за 4-й – 10%. Каков средний
уровень дохода по вкладу за 4 года?
71.
0,05 0,07 0,09 0,10xàðèô ì
0,0775
4
èëè 7,75%
72.
P – первоначальная сумма вкладаi1 , i2 , i3 , i4
- доход по вкладу в первый, второй,
третий и четвертый годы
соответственно (в долях единиц),
F – сумма вклада по истечении четырех
лет.
73.
P i1 1 100 0,05 1 105P i1 1 i2 1
100 0,05 1 0,07 1 112,35
74.
P i1 1 i2 1 i3 1100 0,05 1 0,07 1 0,09 1
122, 4615
75.
F P i1 1 i2 1 i3 1 i4 1100 0,05 1 0,07 1 0,09 1 0,10 1
134,70765
76.
1 i 1 i1 1 i2 1 i3 1 i44
77.
4 (1 i )(1 i )(1 i )(1 i )i
1
1
2
3
4
1,05 1,07 1,09 1,10
4
1,0773282
78.
1 1, 0773282 100 7, 733%n
xгеом x1 x2 ... xn n xi
n
i 1
79.
Пример. В результате инфляции за первыйгод цена товара возросла в два раза к
предыдущему году, а за второй год еще в три
раза к уровню предыдущего года. Ясно, что
за два года цена возросла в 6 раз. Каков
средний темп роста цены за год?
Арифметическая средняя здесь непригодна,
поскольку, если за год цена выросла бы в
(2+3)/2=2,5 раза, то за два года цена выросла
бы в 2,5 *2,5 = 6,25, а не в 6 раз.
Геометрическая средняя даст правильный
ответ:
6
2
,
45
раза.
80.
Пример.Максимальный выигрыш в
лотерее составляет миллион рублей, а
минимальный – сто рублей. Какую
величину можно считать средней между
миллионом и сотней? Арифметическая
средняя явно непригодна, так как
составляет 500050 рублей, а это, как и
миллион, крупный, а никак не средний
выигрыш. Геометрическая средняя в
этом случае дает наиболее правильный
с точки зрения экономики и логики
ответ:
100 100000 10000





















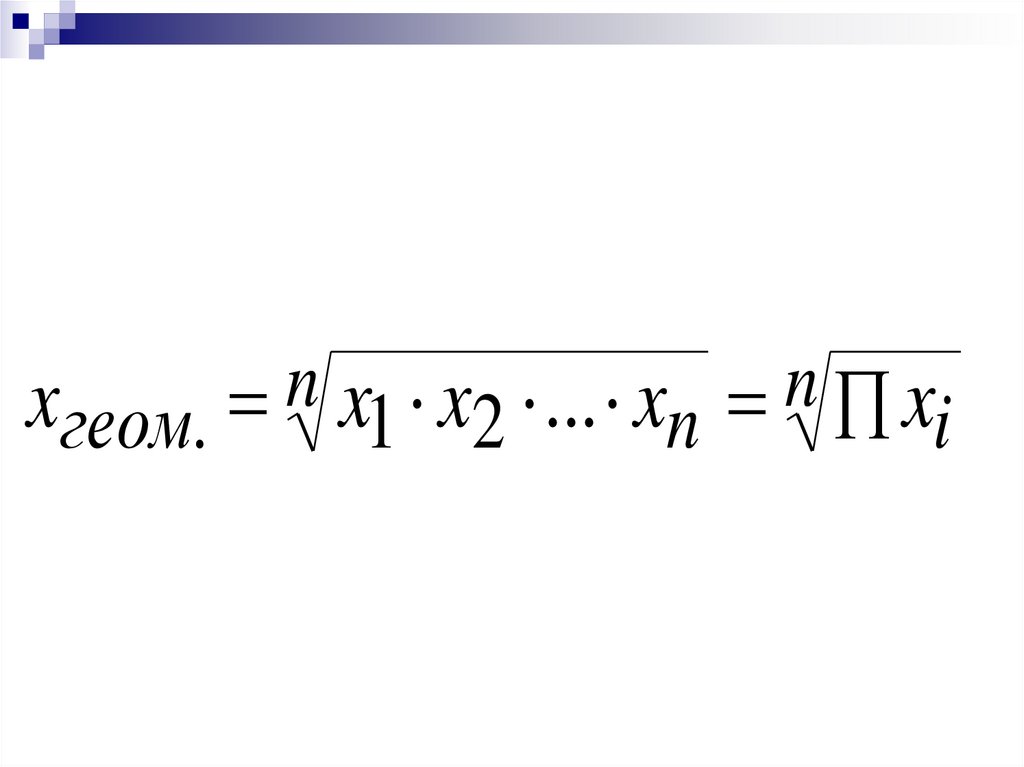
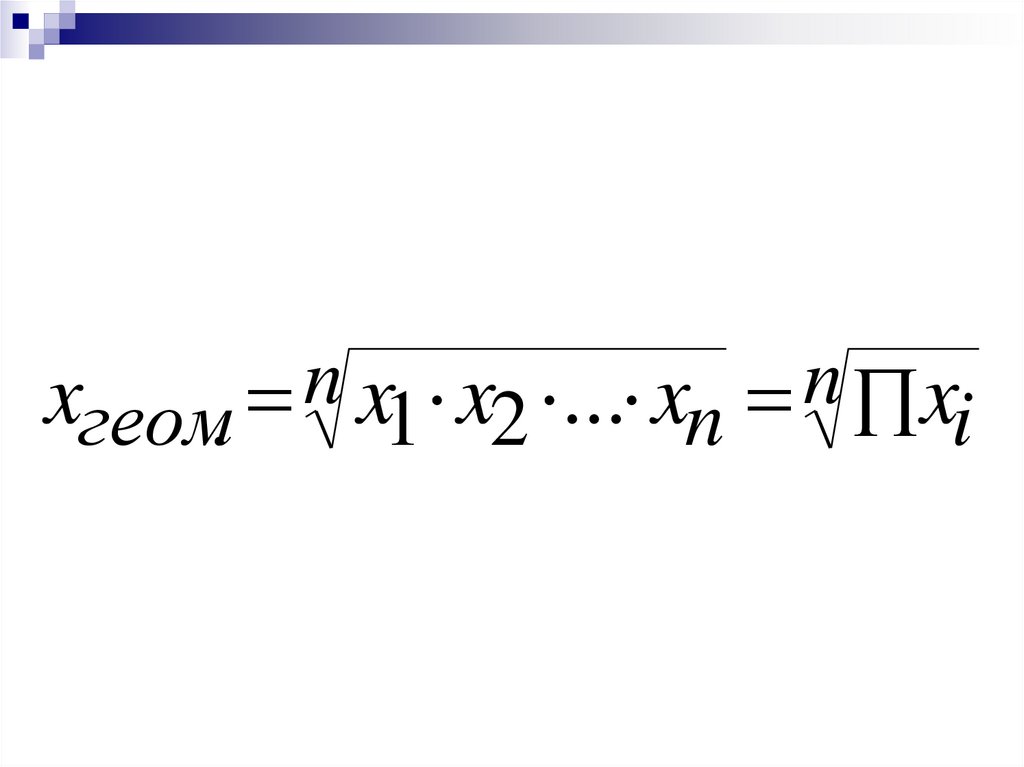

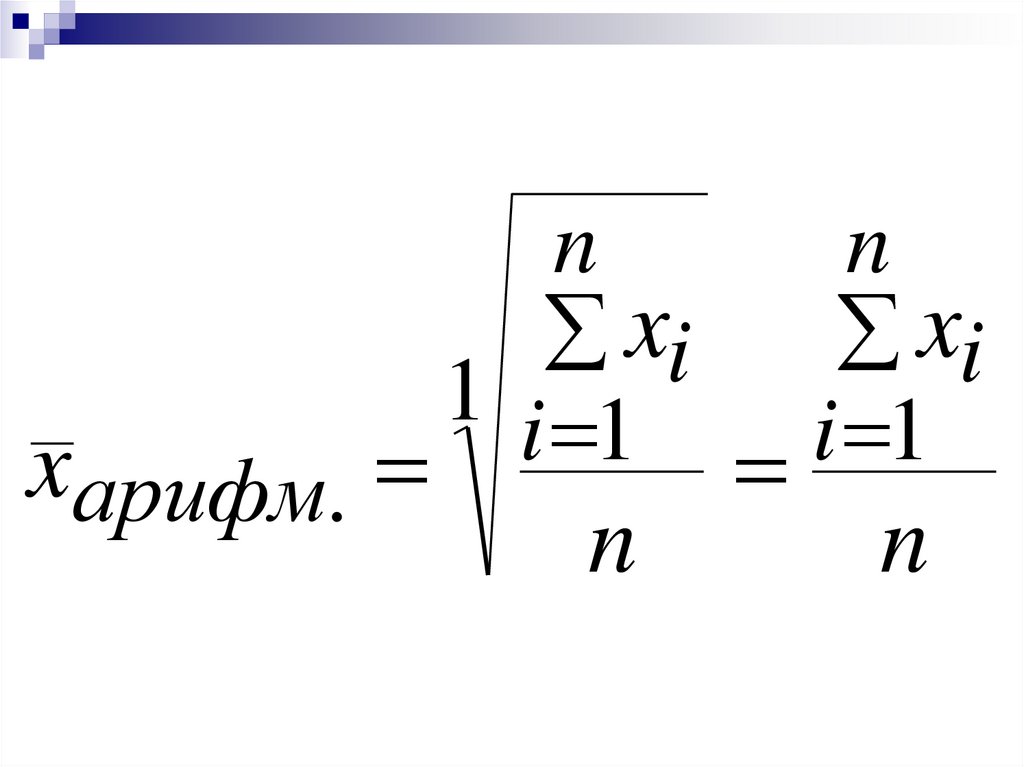
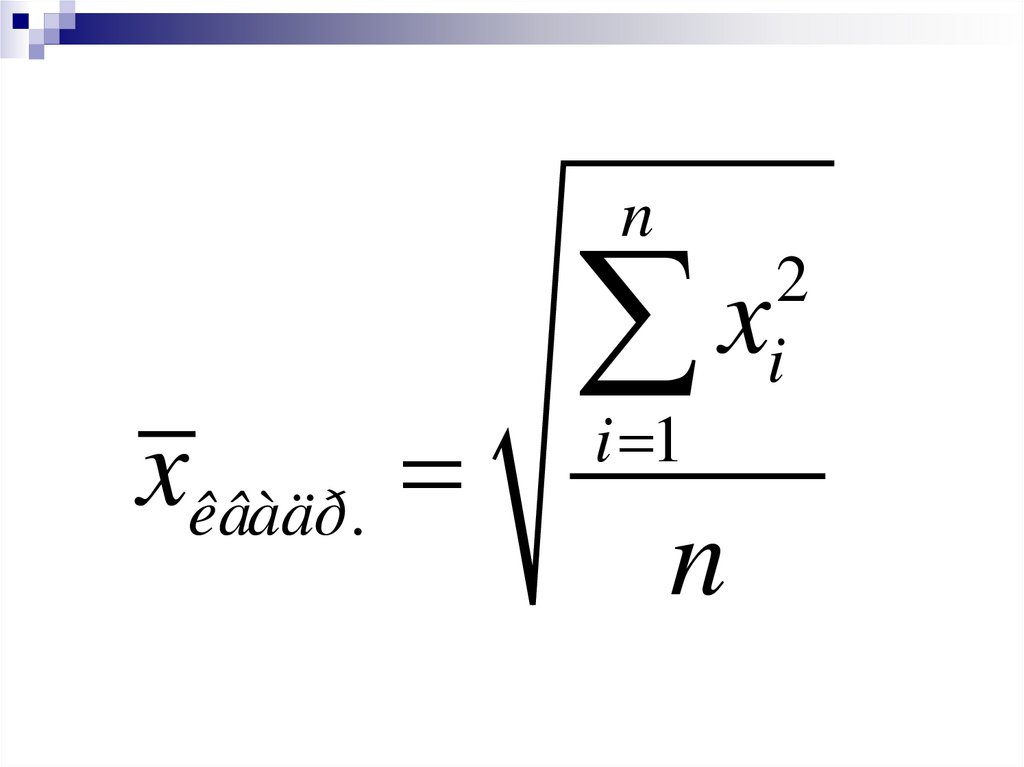
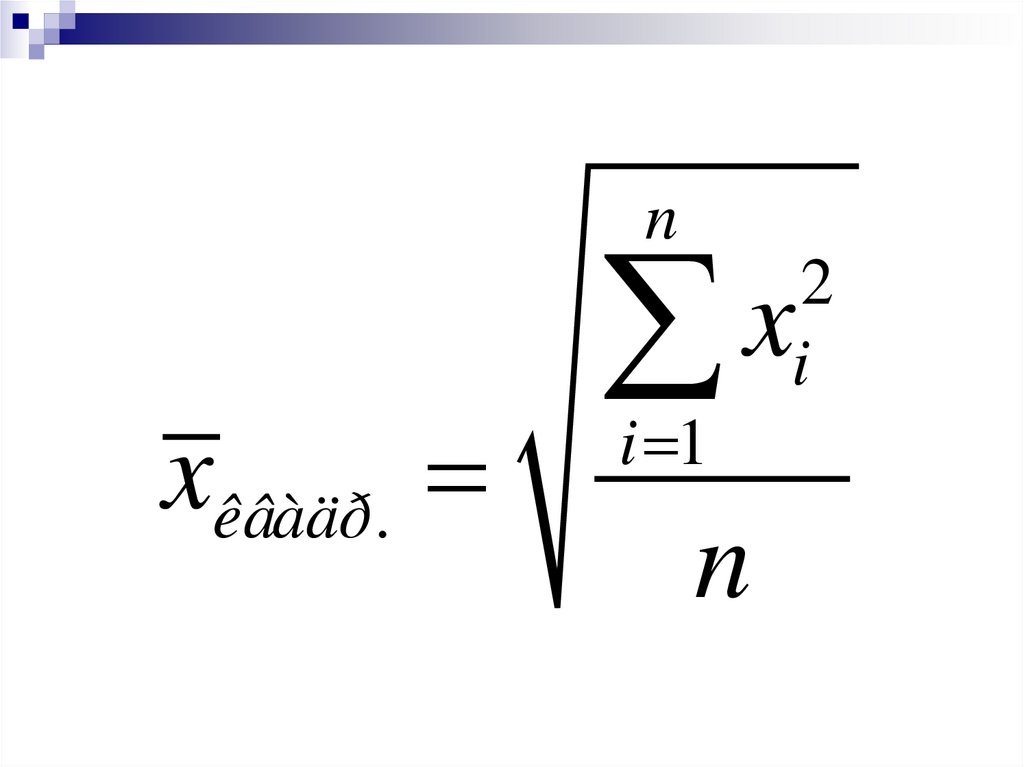





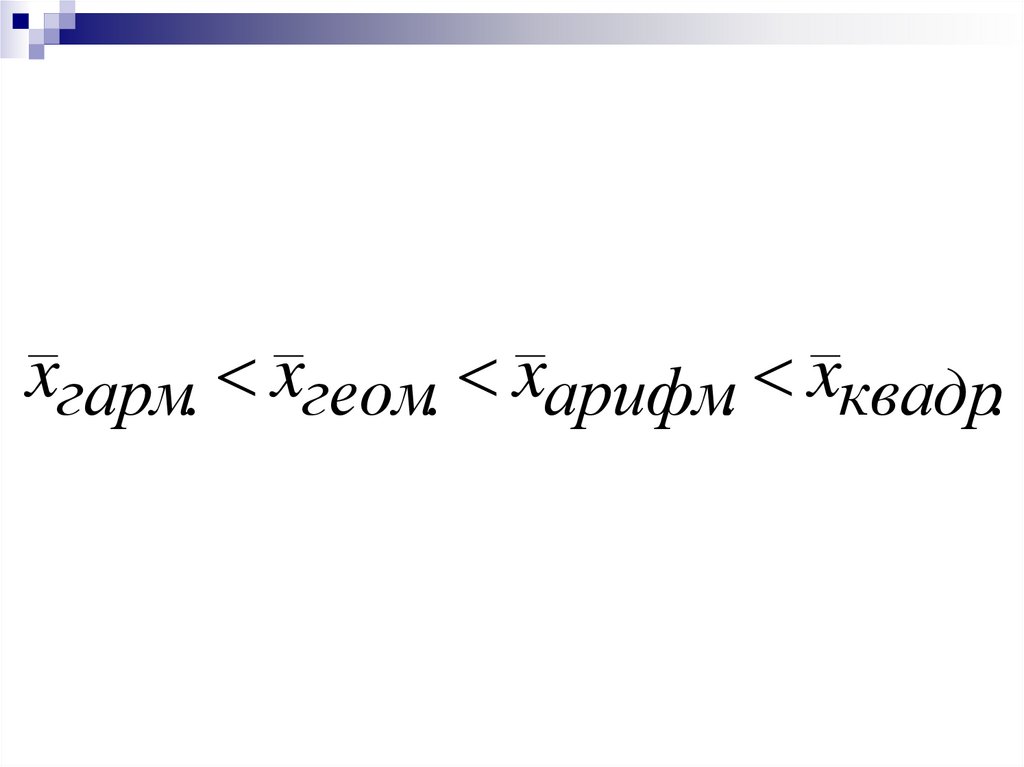


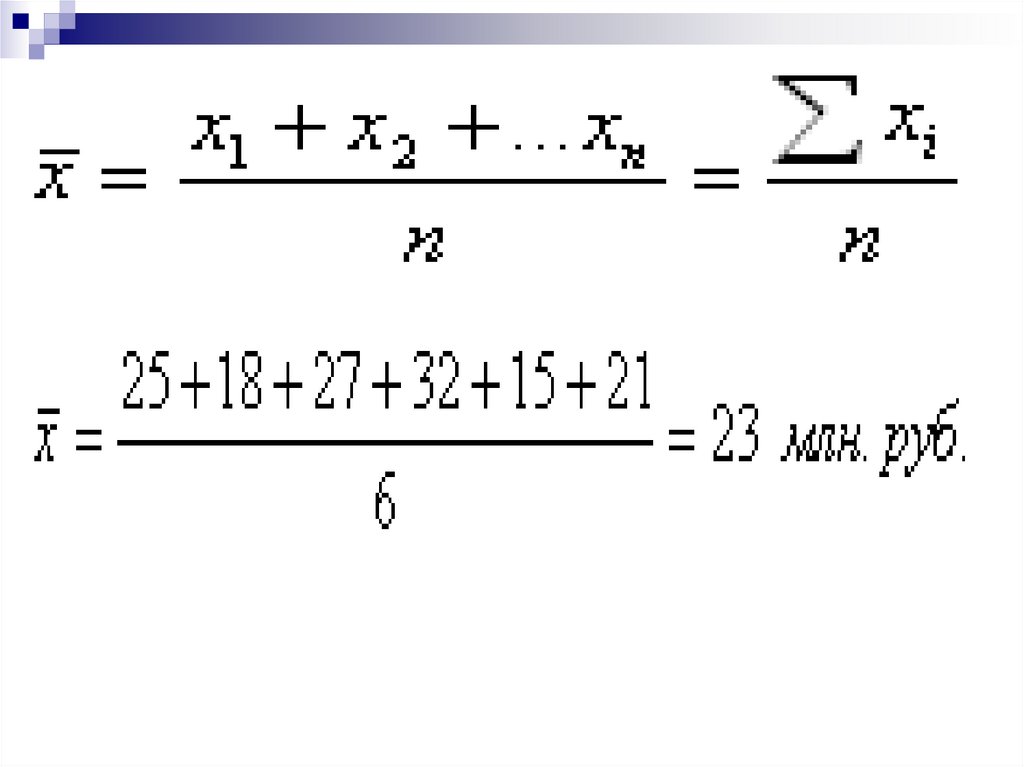


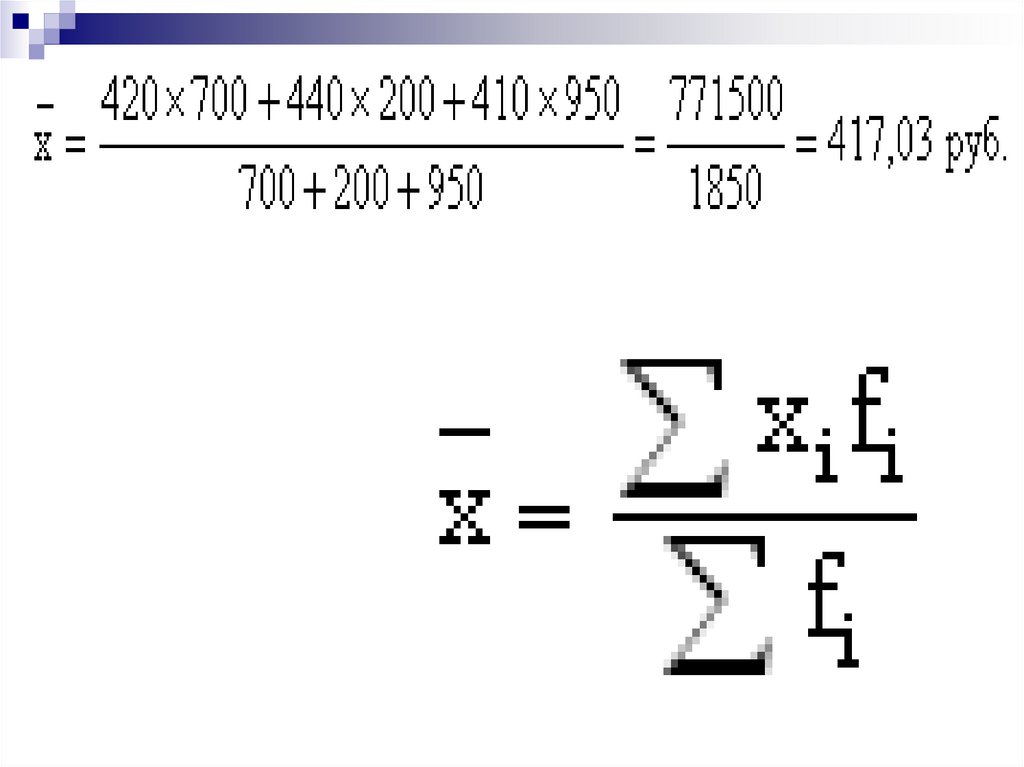


















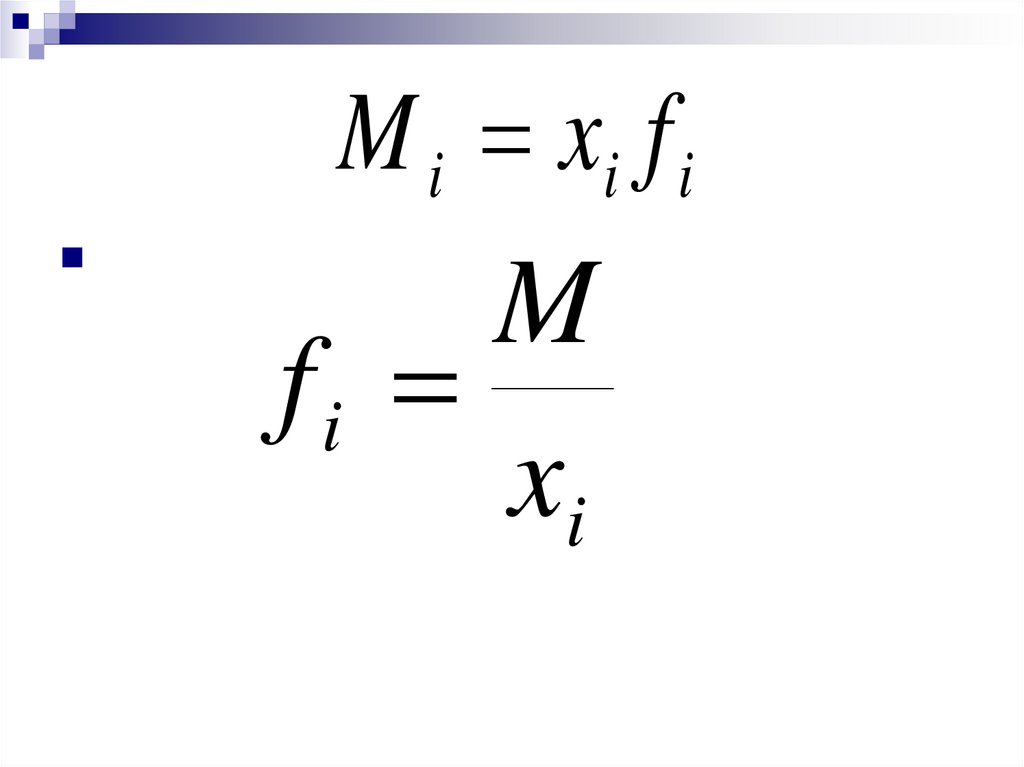

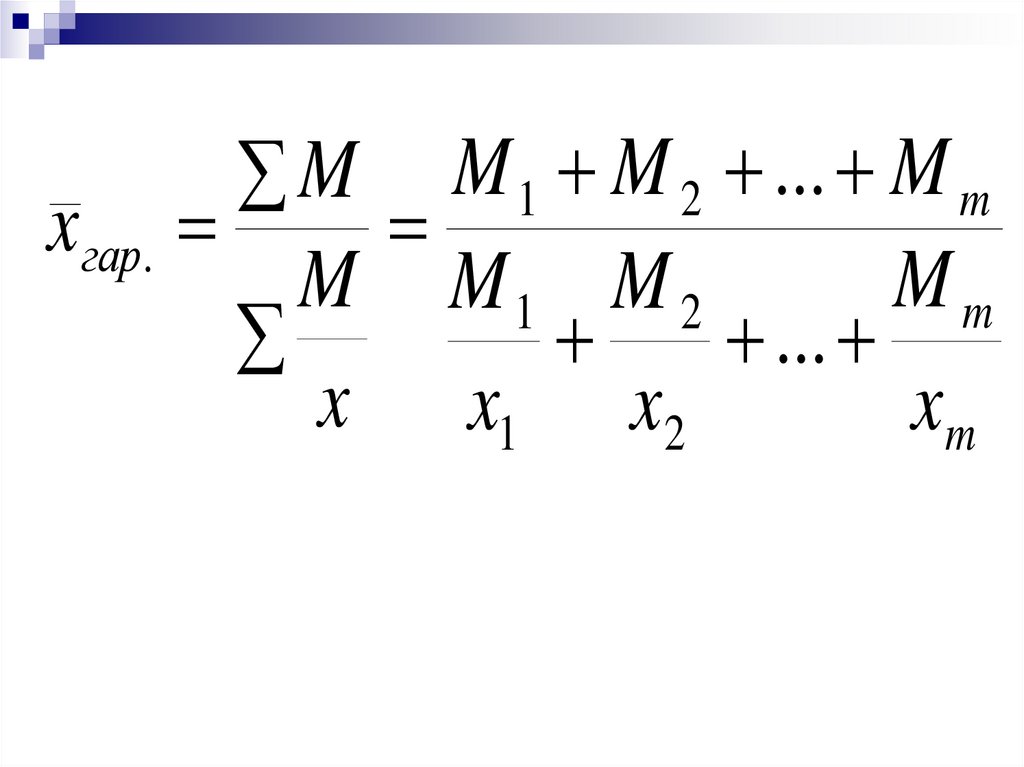
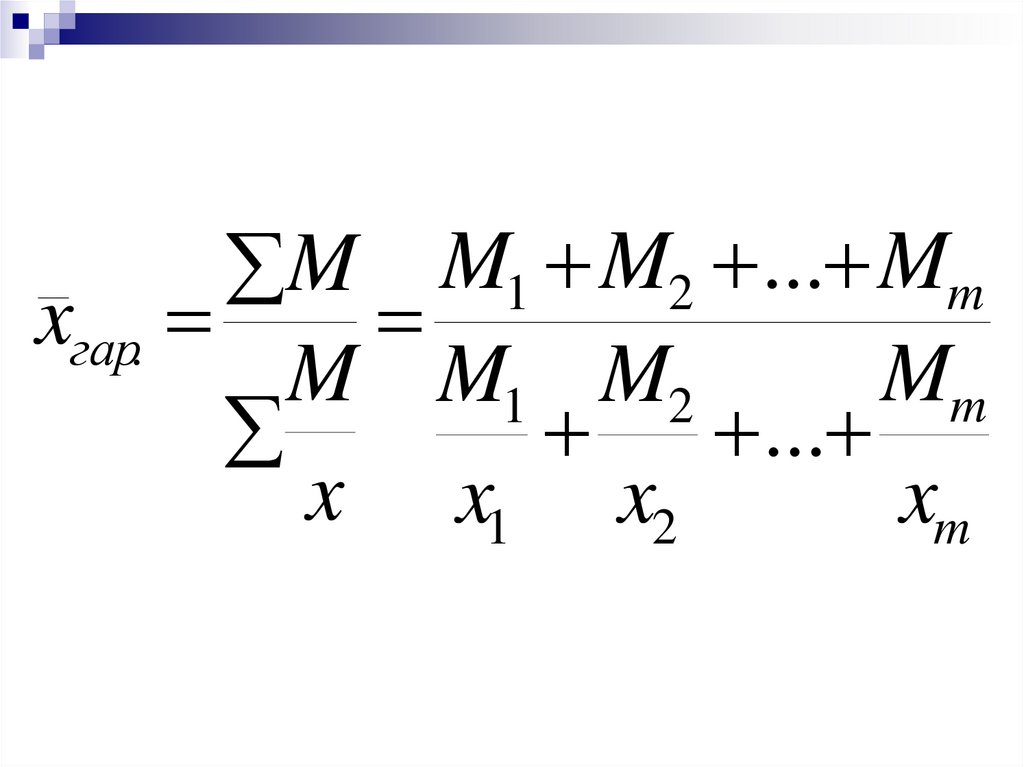







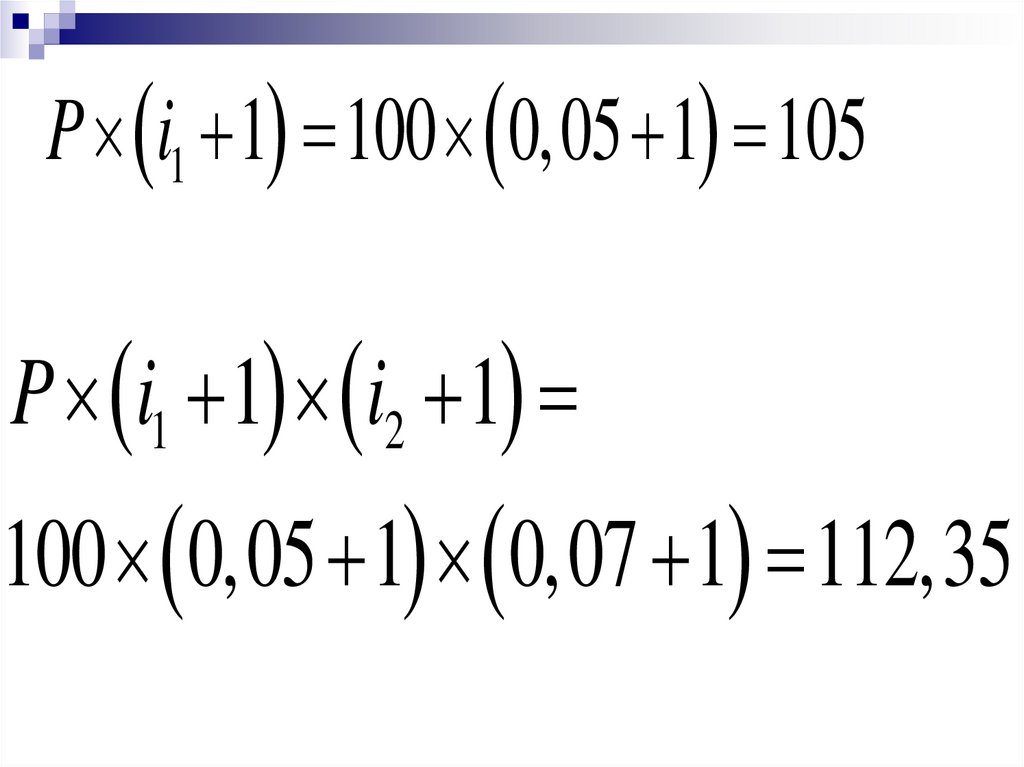


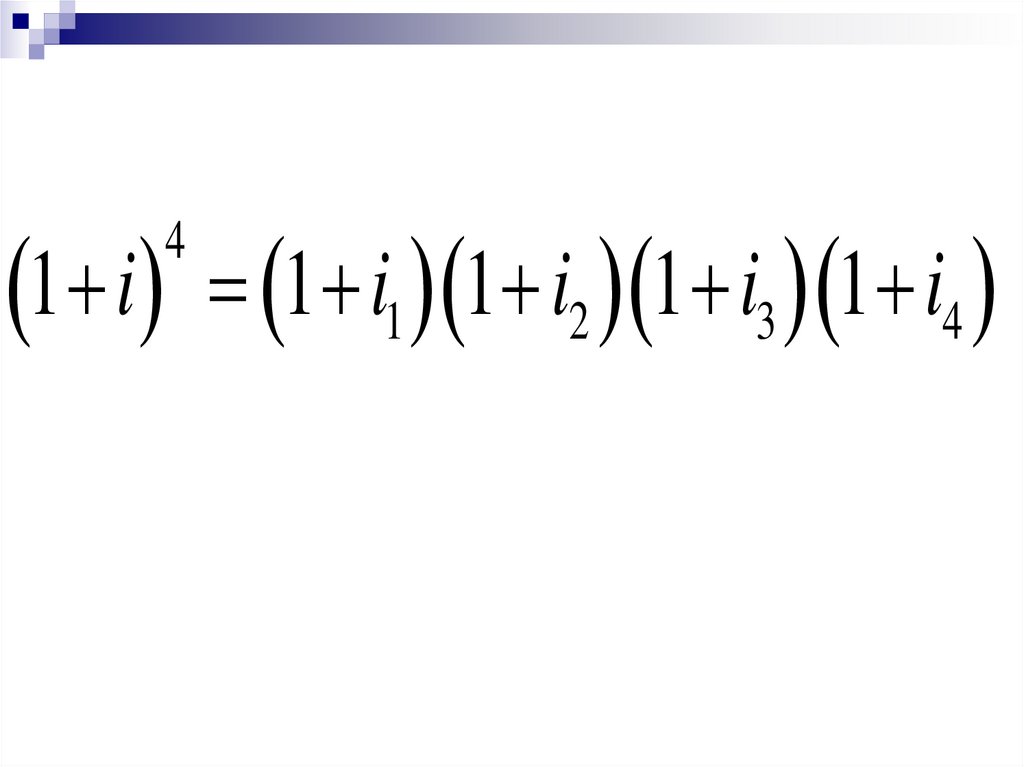




 mathematics
mathematics








