Теорема Пифагора

1.

2.

1. Немного истории
2. Теорема Пифагора
3. Доказательства теоремы:
I способ (классический);
II способ (доказательство Бхаскары);
III способ (доказательство Анариция);
4. Задачи
повторяем

3.

Знаменитый древнегреческий ученый Пифагор
жил в VI в. до н.э.(около 570-500 г.г.).Он родился
на острове Самос в Эгейском море. В молодые
годы много странствовал; долго жил в Египте,
затем в Вавилоне.Последний период своей жизни
(примерно с 530 г. до н.э.) Пифагор прожил в
городе Кротон–греческой колонии на юге Италии.
Здесь он создал знаменитую Пифагорейскую
школу. Исследования Пифагора
охватывали астрономию, музыку,
арифметику и геометрию. Пифагор
был убит, а его школа разгромлена
когда к власти пришли сторонники
рабовладельческой демократии.

4.

История теоремы начинается задолго до
Пифагора. В вавилонских текстах эта
теорема встречается за 1200 лет до
Пифагора. Возможно тогда ещё не знали
её доказательства, а соотношение было
установлено опытным путём. За 2000 лет
до н. э. египтяне пользовались этим
отношением для построения прямых углов. Эта теорема
была известна в Китае и древней Индии. О ней писали в своих
произведениях римский архитектор и инженер Витрувий,
греческий историк Плутарх, греческий
учёный III в. Диоген Лаэрций, математик
V в. Прокл и многие другие.
Пифагор же нашел доказательство этого
соотношения и поэтому теорема стала
называться его именем.

5.

У арабских математиков теорема
Пифагора называлась «теоремой
невесты», так как чертеж к ней
напоминает пчелу или крылатого
муравья. Древние греки так называли
молодых женщин, невест, а арабы
сделали соответствующий перевод.
Доказательство теоремы Пифагора
среди учащихся средних веков
считалось очень трудным и поэтому
теорема называлась Pons asinorum «Мост ослов». Слабые ученики, заучивавшие теорему
наизусть без понимания и прозванные поэтому «ослами» не
были в состоянии преодолеть теорему Пифагора, служившую
для них вроде непроходимого моста.

6.

Вернемся к рассмотрению непосредственно теоремы Пифагора.
В настоящее время её формулировка выглядит так:
«В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов».
a
c
c2 = a2 + b2
b
На протяжении веков были найдены различные доказательства
теоремы Пифагора. В настоящее время их насчитывают более ста.
Рассмотрим некоторые из них.

7.

I способ (классический)
c
a
b
а
b
a
b
a
c
c
c
b
c
b
a
Рассмотрим прямоугольный треугольник c
катетами а, b и гипотенузой с.
Докажем, что с2 = а2 + b2.
Достроим треугольник до квадрата
со стороной а + b.
Площадь S этого квадрата равна (а +b)2.
С другой стороны, этот квадрат составлен из
четырех равных прямоугольных треугольников,
площадь каждого из которых равна ab , и
2
квадрата со стороной с, площадь которого равна
с2, поэтому S 4 ab c2 2ab c2
2
Таким образом, (а + b )2 = 2аb + с2,
а2 + 2аb + b2 = 2ab + c2,
откуда с2 = a2 + b2. Что и требовалось доказать.

8.

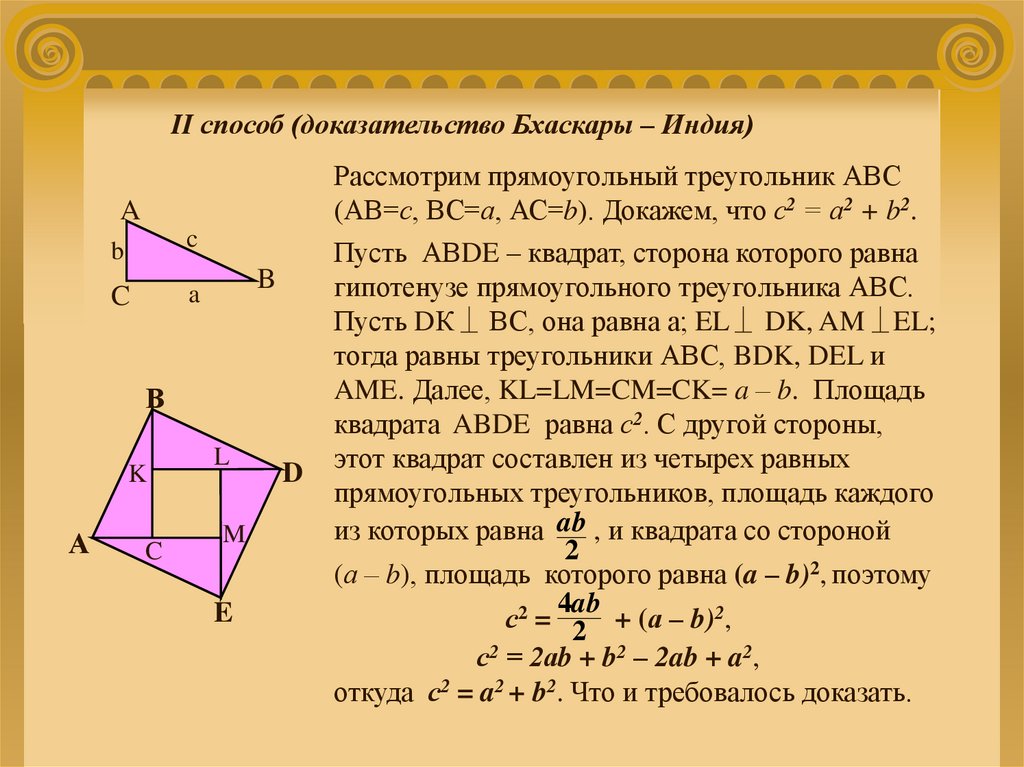
II способ (доказательство Бхаскары – Индия)
A
b
c
C
a
B
В
K
А
C
L
M
E
D
Рассмотрим прямоугольный треугольник АВС
(АВ=с, ВС=а, АС=b). Докажем, что с2 = а2 + b2.
Пусть АВDE – квадрат, сторона которого равна
гипотенузе прямоугольного треугольника АВС.
Пусть DК ВС, она равна а; EL DK, AM EL;
тогда равны треугольники АВС, BDK, DEL и
AME. Далее, KL=LM=CM=CK= a – b. Площадь
квадрата ABDE равна с2. С другой стороны,
этот квадрат составлен из четырех равных
прямоугольных треугольников, площадь каждого
из которых равна ab , и квадрата со стороной
2
(а – b), площадь которого равна (a – b)2, поэтому
4ab
с2 = 2 + (а – b)2,
с2 = 2аb + b2 – 2ab + a2,
откуда с2 = a2 + b2. Что и требовалось доказать.

9. ,

III способ (доказательство Анариция)
Рассмотрим прямоугольный треугольник
АВС, где АВ=с, ВС=а, АС=b. Докажем,
с
что с2 = а2 + b2. Построим квадраты на
катетах и гипотенузе этого треугольника.
В
Эти квадраты разобьем на многоугольники
a
так, что каждому многоугольнику из
М
квадрата на гипотенузе соответствует
равный многоугольник одного из квадратов
4 2
на катетах.
К
Площадь квадрата АВКМ равна с2.
1
Тогда, с2 = S1 + S2 + S3 + S4 +S5.
5
Площадь квадрата СВЕF равна а2 .
3
а2 = S3 + S4 +S5,
В
а площадь квадрата АСRH равна b2.
3
b2 = S1 + S2.
5
Имеем, а2 + b2 = S1 + S2 + S3 + S4 +S5,
4
то есть с2 = а2 + b2. Что и требовалось
E
доказать.
,
А
b
С
А
2
С
F
H
1
R

10.

Найдите неизвестную сторону прямоугольного
треугольника и выберите вариант ответа
4 см
с
3 см
1. 7 см
5 см
3. 25 см
2.

11.

1. 6 дм2
b
8 дм
10 дм
12 дм
3. 6 дм
2.

12.

1 ед
1. 5 ед
2.
3.
3 ед
25 ед
с
2 ед

13.

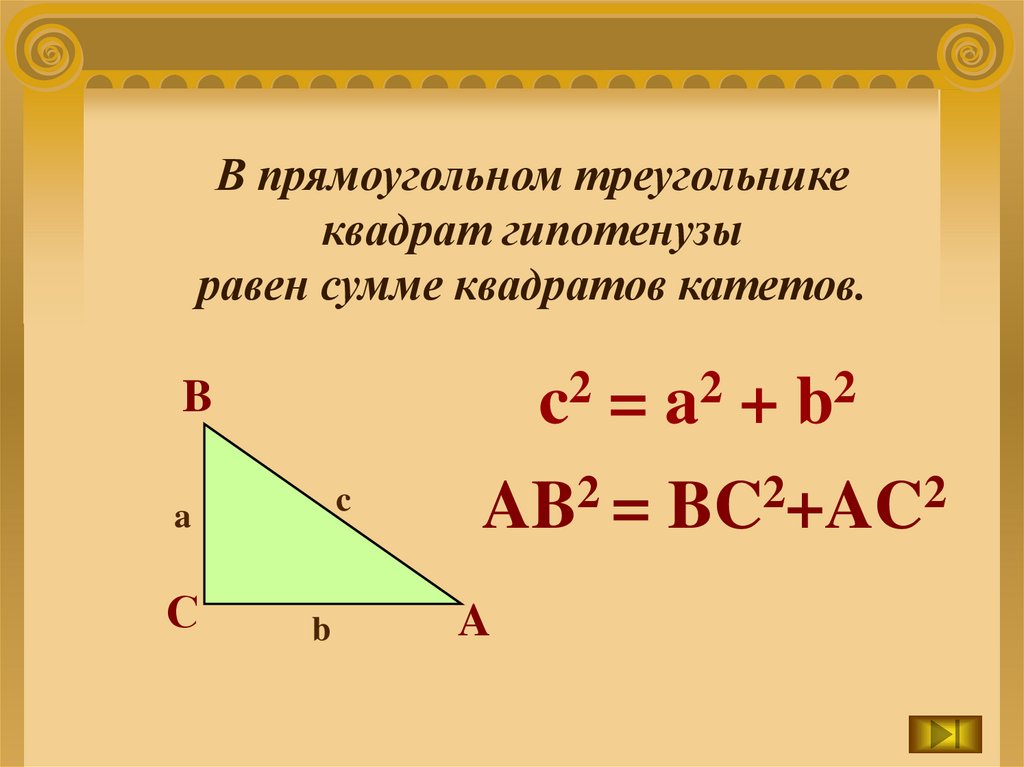
В прямоугольном треугольнике
квадрат гипотенузы
равен сумме квадратов катетов.
2
c
B
c
a
С
b
=
2
a
+
2
b
AB2 = BC2+AC2
A

14.

С помощью рассмотренной теоремы решается очень большое
количество задач. Рассмотрим некоторые из них.
Задача: Найдите высоты треугольника, зная, что его
стороны равны 7см, 8см, 9 см.
А
Рассмотрим АВС, где АВ=9см, ВС=8см,АС=7см.
Требуется найти его высоты hАВ, hВС, hАС.
х
В
С
Пусть AD - искомая высота.
D
Обозначим через х отрезок ВD. Тогда CD = 8 – х.
АВ2 = AD2+BD2 и АС2 = AD2+CD2 (по т.Пифагора), тогда
AD2 = AB2 – BD2 и AD2 = AC2 – CD2. Получим:
AB2 – BD2 = AC2 – CD2
81 – х2 = 49 – (8 – х)2.
Решая уравнение, получим х = 6.
Так как BD=6, то AD2 = 81 – 36 = 45, то есть AD=3 5см.
Две другие высоты этого треугольника найдите самостоятельно.

15.

Теорема Пифагора выражает свойство
прямоугольного треугольника. Обратное ей утверждение
является признаком прямоугольного треугольника.
«Если в треугольнике квадрат стороны равен сумме
квадратов двух других его сторон, то такой
треугольник прямоугольный»
С
А
АС2 +ВС2 = АВ2
В
АВС - прямоугольный

16.

Теорему Пифагора и обратную ей теорему можно применять и в
практических целях.
Задача : На местности с помощью веревки построить
прямой угол.
5
3
4
Применяя обратную
теорему Пифагора
можно увидеть, что
треугольник со сторонами 3, 4 и 5 является
прямоугольным,так как 52 = 32+42. Поэтому
поступают так: на веревке делают метки,
делящие её на 12 равных частей (3+4+5=12);
связывают концы и растягивают на Земле с
помощью кольев в виде треугольника со
сторонами 3, 4 и 5. Тогда угол между
сторонами 3 и 4 оказывается прямым.

17.

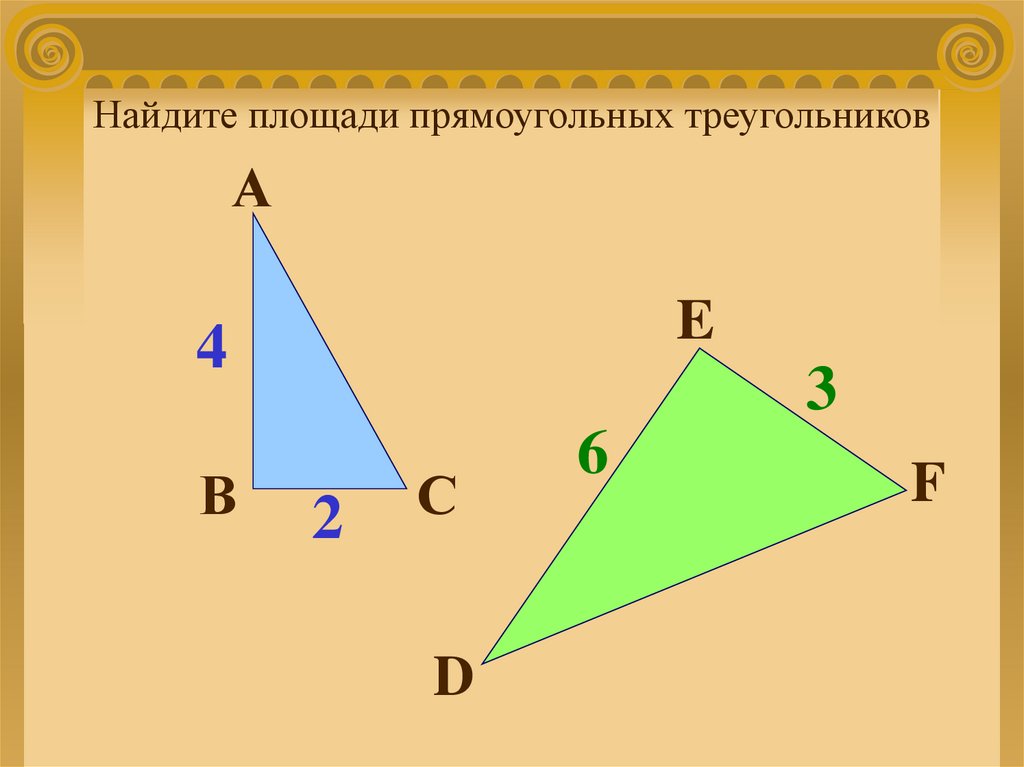
Найдите площади прямоугольных треугольников
А
E
4
В
3
2
С
D
6
F

18.

N
T
8
S
8
T
3
R
K
4
C
3
F
6
M

19.

1 + 3 = 2
2–?
2
1
3

20.

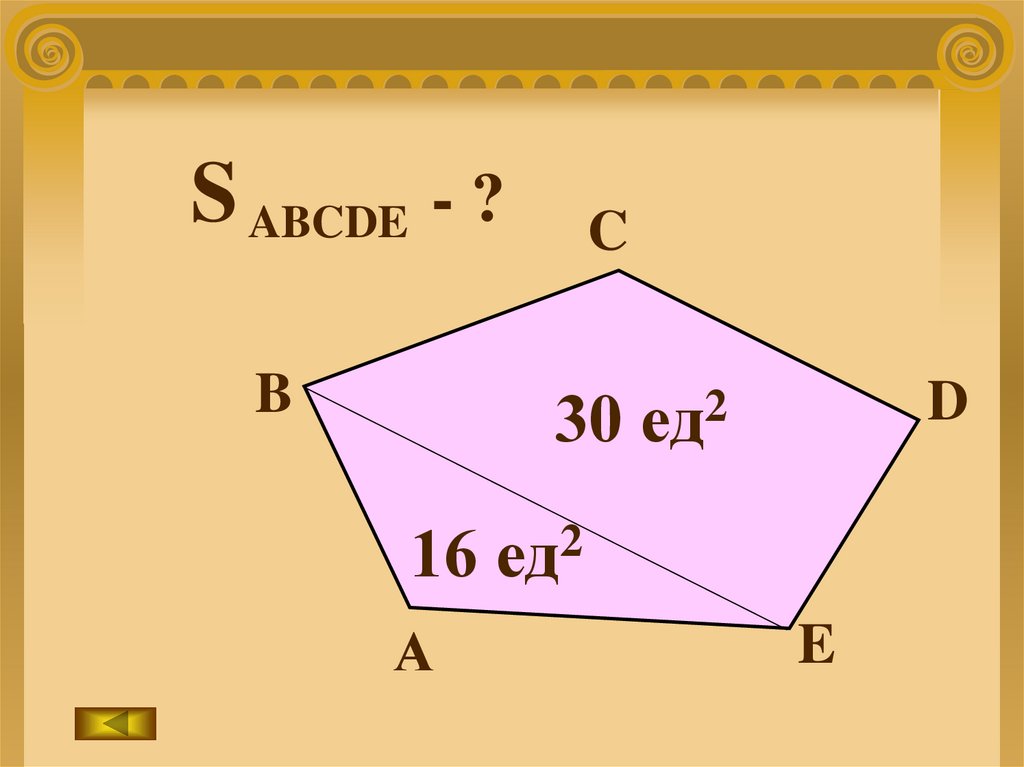
S ABCDE - ?
B
C
30
16
А
ед2
D
2
ед
E

21.

Неверно !

22.

Молодец !