Similar presentations:
Теорема Пифагора
1.
ТеоремаПифагора
К учебнику Л.С. Атанасяна
Геометрия 7-9, Глава VI, пп.55,56
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская ООШ»
Оршанского района Республики Марий Эл
2.
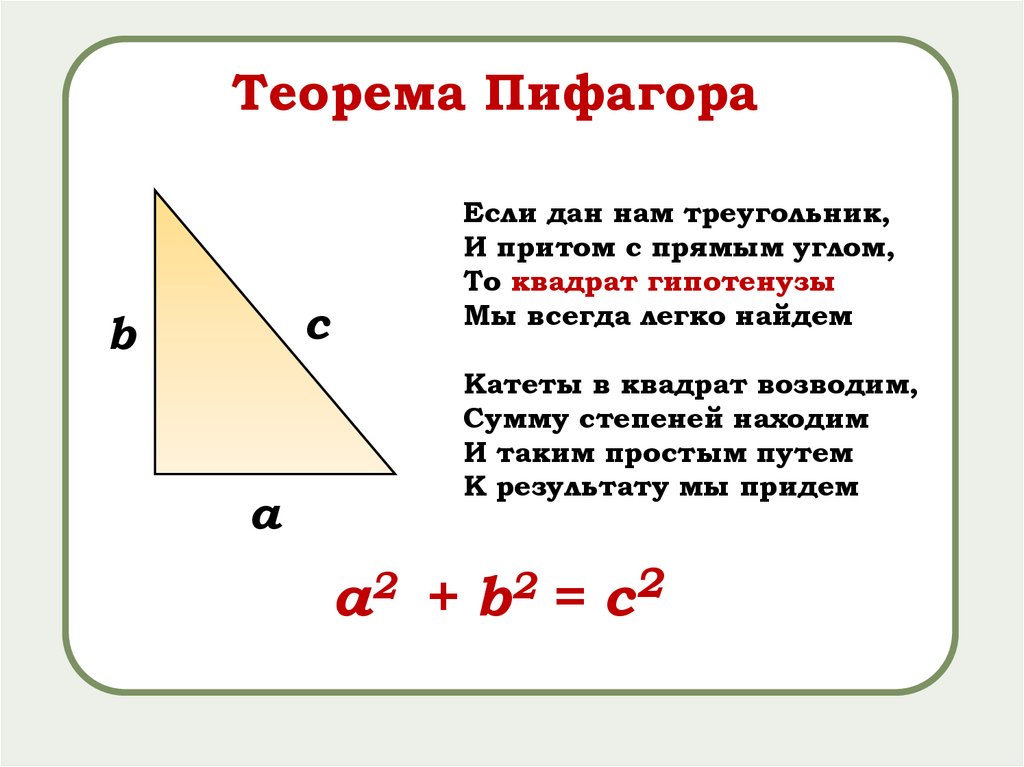
Теорема Пифагораc
b
a
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путем
К результату мы придем
2
2
2
a +b =c
3.
Пифагор: «Я не учумудрости, я исцеляю от
невежества.»
ПИФАГОРОВЫ ЗАКОНЫ
Сыщи себе верного друга;
имея его, ты можешь обойтись
без богов.
Делай лишь то, что
впоследствии не омрачит тебя
и не заставит раскаиваться.
Не пренебрегай здоровьем
своего тела.
Научись жить просто и без
роскоши.
Либо молчи, либо говори то,
что ценнее молчания.
Пифагор Самосский
570 - 480 гг. до н. э
древнегреческий
философ и
математик,
создатель
религиознофилософской
школы
пифагорейцев
4.
Историческийанекдот:
Когда
Пифагор доказал свою теорему, он
в благодарность богам принёс в
жертву 100 быков, и с тех пор все
скоты ненавидят математику.
Шаржи на
теорему
Другие названия
теоремы:
Пифагоровы штаны
Теорема нимфы
Теорема невесты
Ветряная мельница
Ослиный мост
Бегство убогих
5.
c2а2
b2
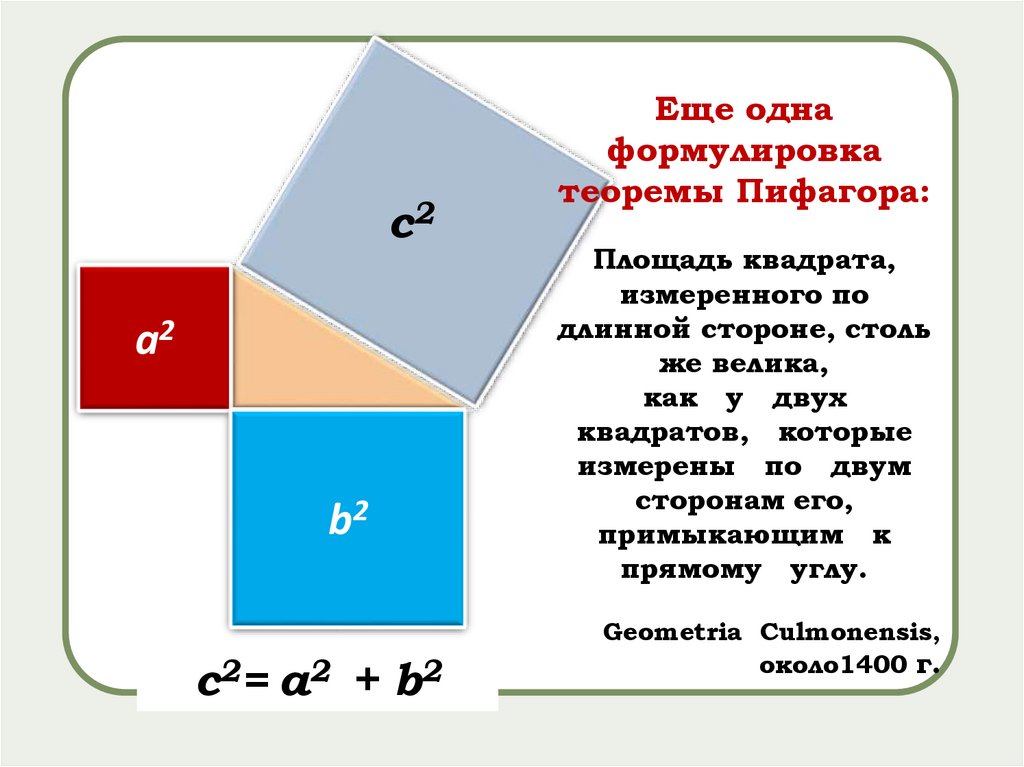
c2= a2 + b2
Еще одна
формулировка
теоремы Пифагора:
Площадь квадрата,
измеренного по
длинной стороне, столь
же велика,
как у двух
квадратов, которые
измерены по двум
сторонам его,
примыкающим к
прямому углу.
Geometria Culmonensis,
около1400 г.
6.
Доказательство теоремы, дающей зависимость между катетамии гипотенузой прямоугольного треугольника, по мнению античных
авторов нашей эры (Диоген, Порфирий, Афиней, Плутарх),
принадлежит Пифагору или кому-то из его учеников. Каким оно
было? История не дает ответа на этот вопрос. До нас дошли
несколько доказательств этой теоремы, приведенных в «Началах»
Евклида. Более ранние доказательства теоремы Пифагора, за
исключением частных случаев, истории математики неизвестны.
На протяжении многих веков предпринимались тысячи попыток
найти новые способы доказательство теоремы Пифагора. И они
были найдены.
На данный момент в научной литературе
зафиксировано около 400 доказательств данной теоремы. Не
существует другой теоремы с такой богатой историей, которая
бы пользовалась таким вниманием математиков и любителей
математики. Интерес к теореме вызывается еще и тем, что она
является одной из основополагающих теорем евклидовой
геометрии, применяется буквально на каждом шагу. Теорему
Пифагора называют жемчужиной античной математики. Причина
ее популярности – простота, красота, значимость.
7.
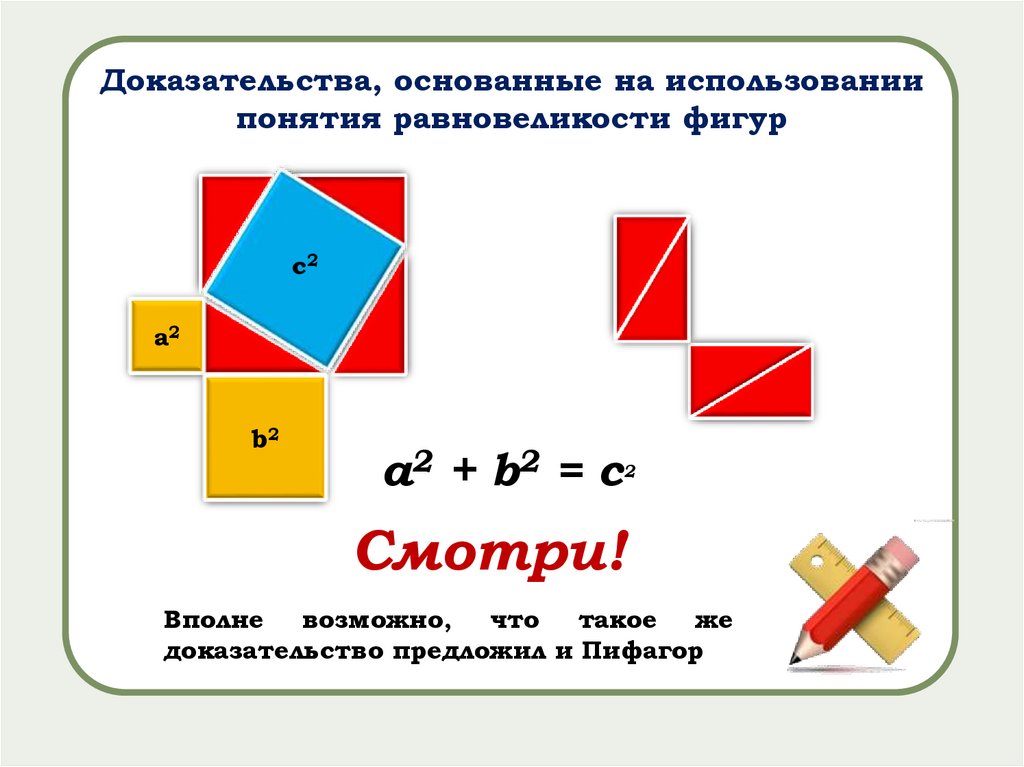
Доказательства, основанные на использованиипонятия равновеликости фигур
с2
a2
b2
а2 + b2 = с
2
Смотри!
Вполне возможно, что такое же
доказательство предложил и Пифагор
8.
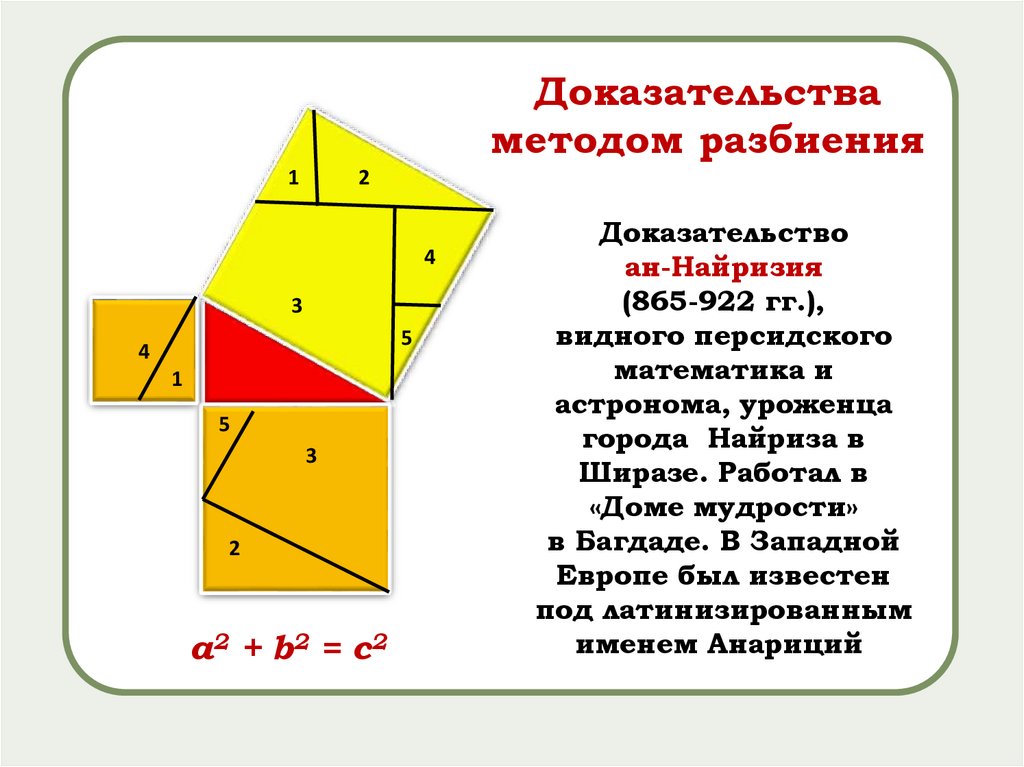
Доказательстваметодом разбиения
1
2
4
3
5
4
1
5
3
2
а2 + b2 = с2
Доказательство
ан-Найризия
(865-922 гг.),
видного персидского
математика и
астронома, уроженца
города Найриза в
Ширазе. Работал в
«Доме мудрости»
в Багдаде. В Западной
Европе был известен
под латинизированным
именем Анариций
9.
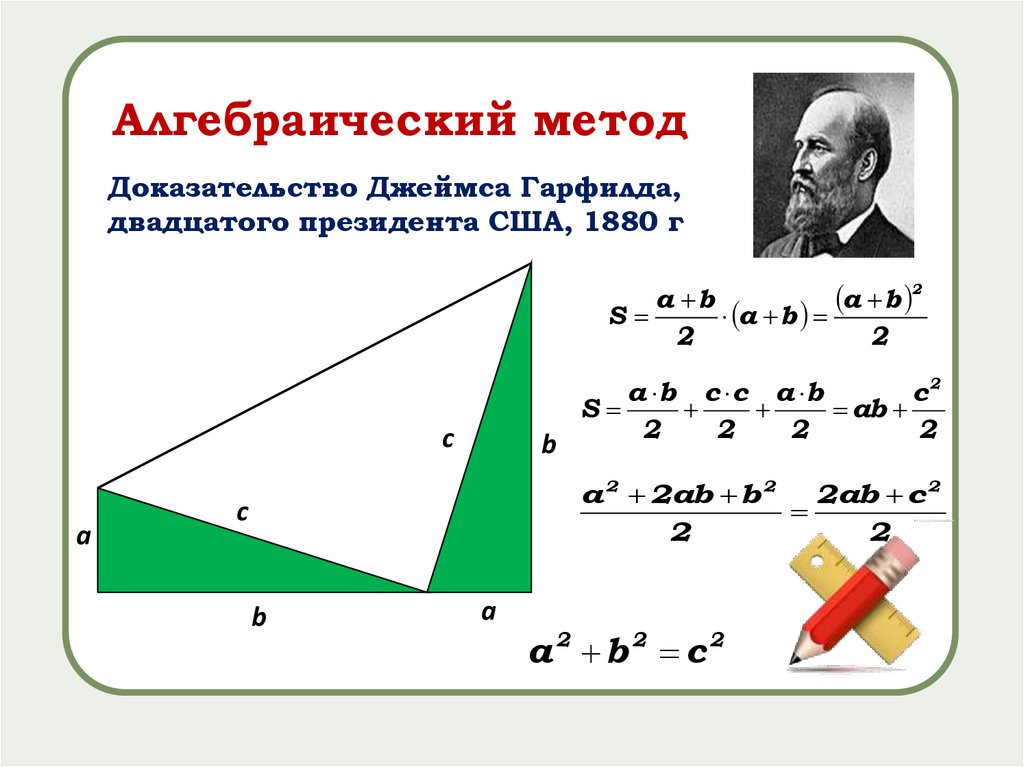
Алгебраический методДоказательство Джеймса Гарфилда,
двадцатого президента США, 1880 г
a b
a b
S
a b
2
2
2
c
а
b
a b с с a b
c2
S
ab
2
2
2
2
a 2 2ab b 2
2ab c 2
2
2
c
b
a
a2 b2 c2
10.
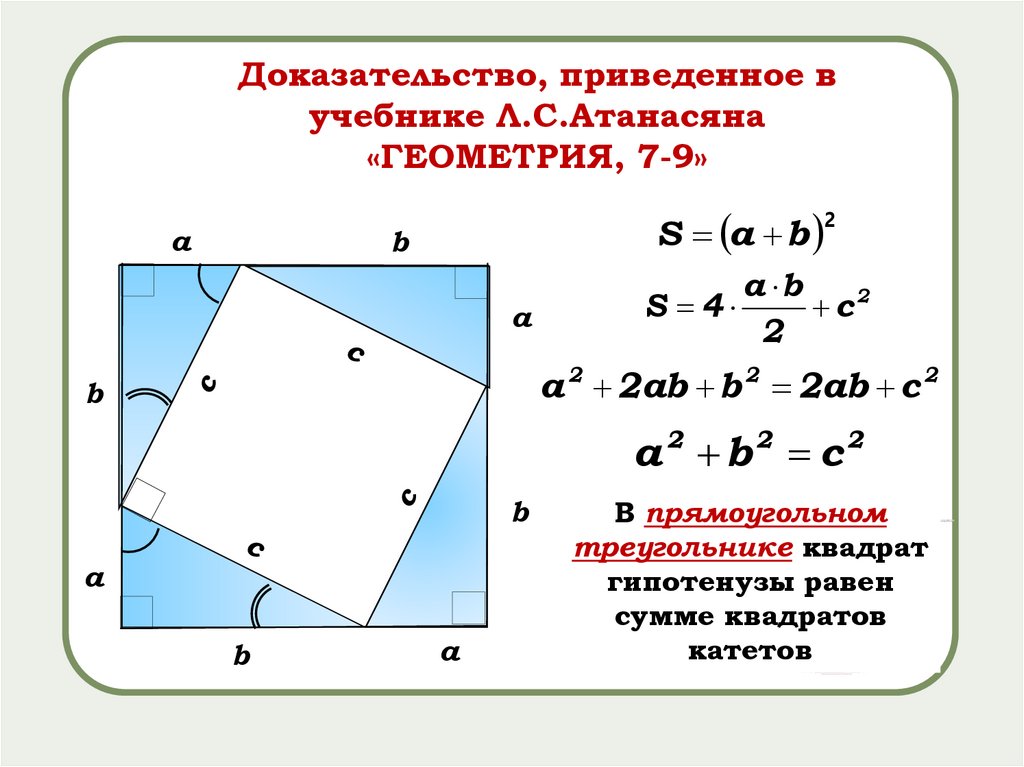
Доказательство, приведенное вучебнике Л.С.Атанасяна
«ГЕОМЕТРИЯ, 7-9»
a
S a b
2
b
a
S 4
a b
c2
2
a 2 2ab b 2 2ab c 2
b
a b c
2
b
а
b
a
2
2
В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетов
11.
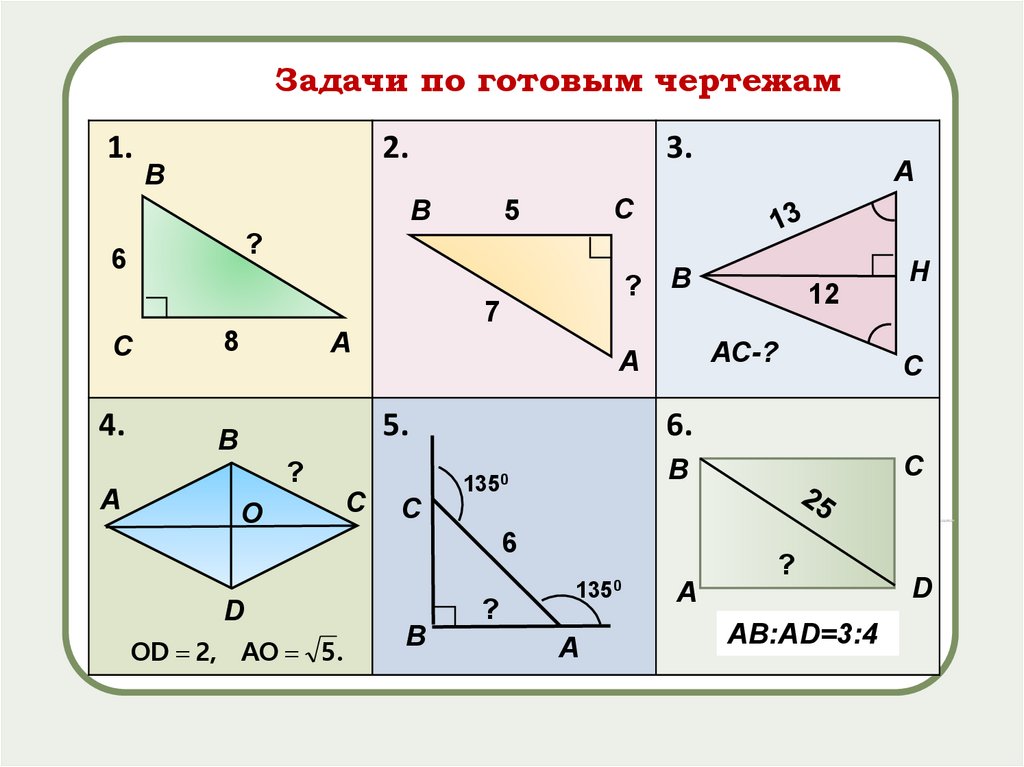
Задачи по готовым чертежам1.
2.
В
3.
В
∟
∟
8
4.
В
? В
7
А
О
С
С
В
С
?
С
В
1350
∟
OD 2, AO 5.
Н
6.
6
D
12
АС-?
А
5.
?
∟
С
А
С
5
?
6
А
1350
А
А
?
АВ:AD=3:4
D
12.
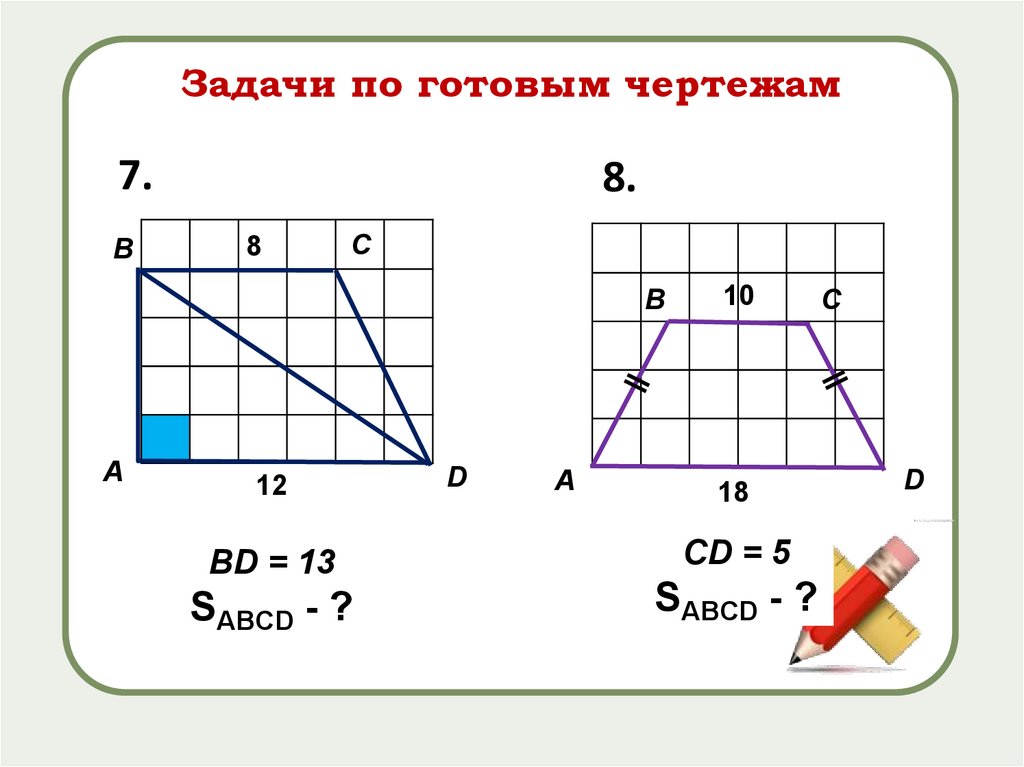
Задачи по готовым чертежам7.
В
8.
8
С
В
А
12
D
А
10
18
BD = 13
СD = 5
SABCD - ?
SABCD - ?
С
D
13.
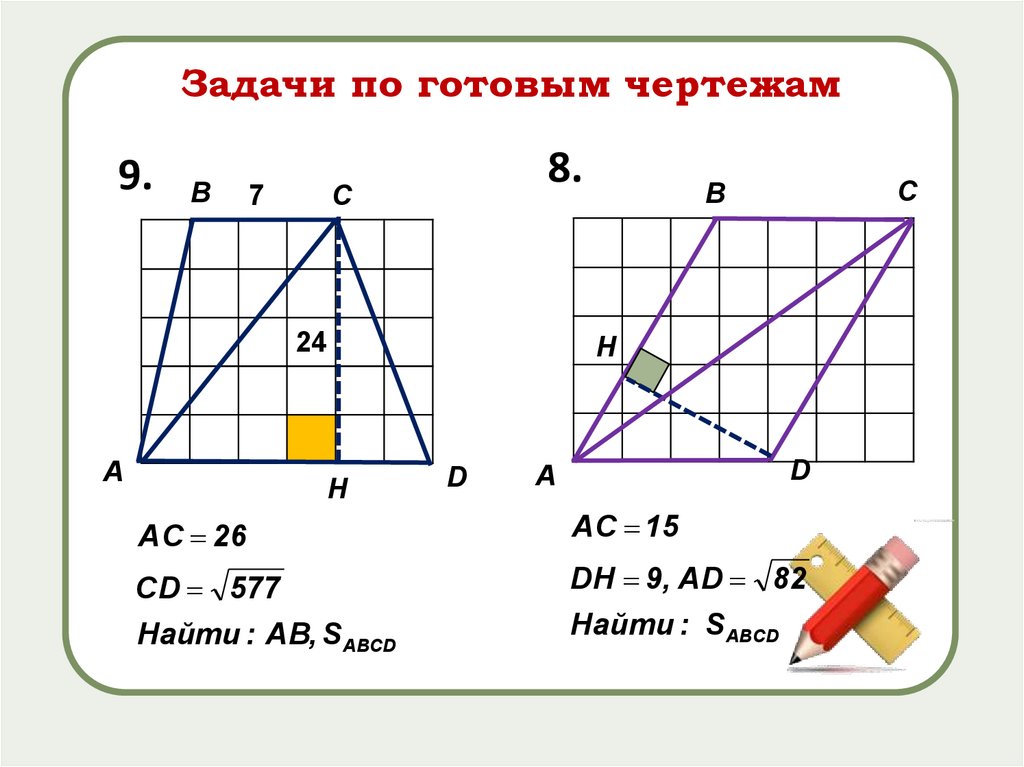
Задачи по готовым чертежам9.
В
8.
С
7
24
А
H
С
В
H
D
А
D
AC 26
AC 15
CD 577
Найти : АВ, SABCD
DH 9, AD 82
Найти : SABCD
14.
Теорема, обратная теореме ПифагораТеорема
Если
треугольник
Теорема Пифагора:
Пифагора: В
прямоугольном
прямоугольный,
квадратгипотенузы
гипотенузы
треугольнике то
квадрат
равен
равенсумме
суммеквадратов
квадратовкатетов
катетов
Обратное утверждение: Если квадрат
одной стороны треугольника
равен
сумме квадратов двух других сторон,
то треугольник прямоугольный
15.
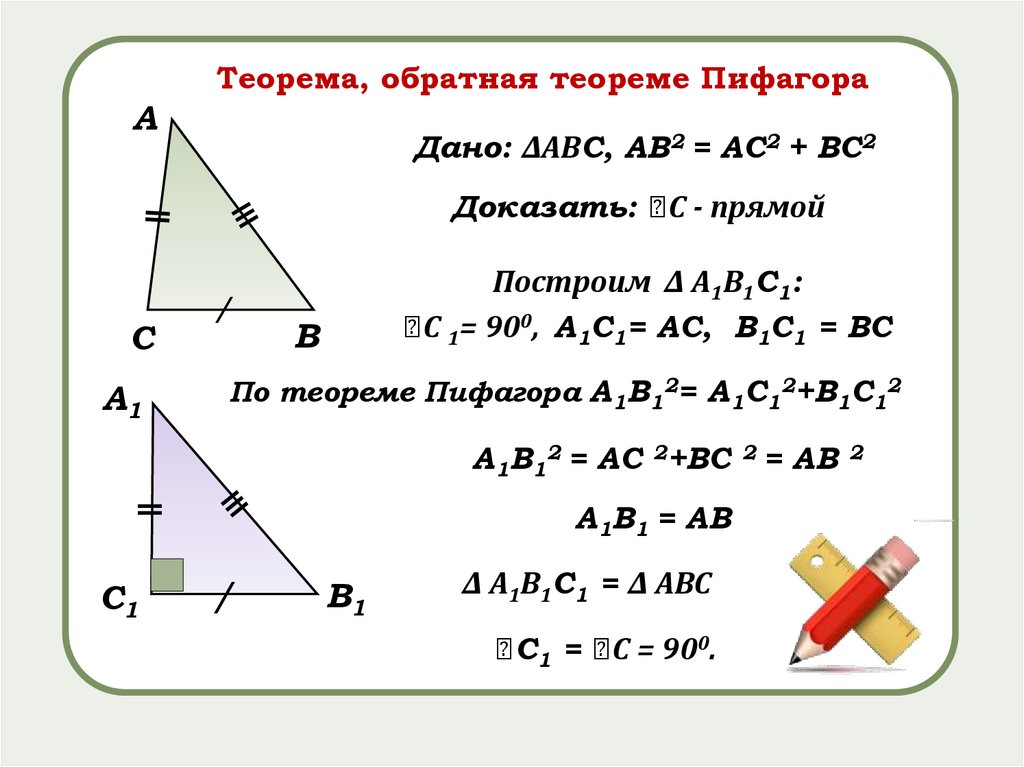
Теорема, обратная теореме ПифагораА
Дано: ΔАВС, АВ2 = АС2 + ВС2
Доказать: ∠С - прямой
С
А1
/
Построим Δ А1В1С1:
∠С 1= 900, А1С1= АС, В1С1 = ВС
В
По теореме Пифагора А1В12= А1С12+В1С12
А1В12 = АС 2+ВС 2 = АВ 2
ǁ
А1В1 = АВ
С1
/
В1
Δ А1В1С1 = Δ АВС
∠С1 = ∠С = 900.
16.
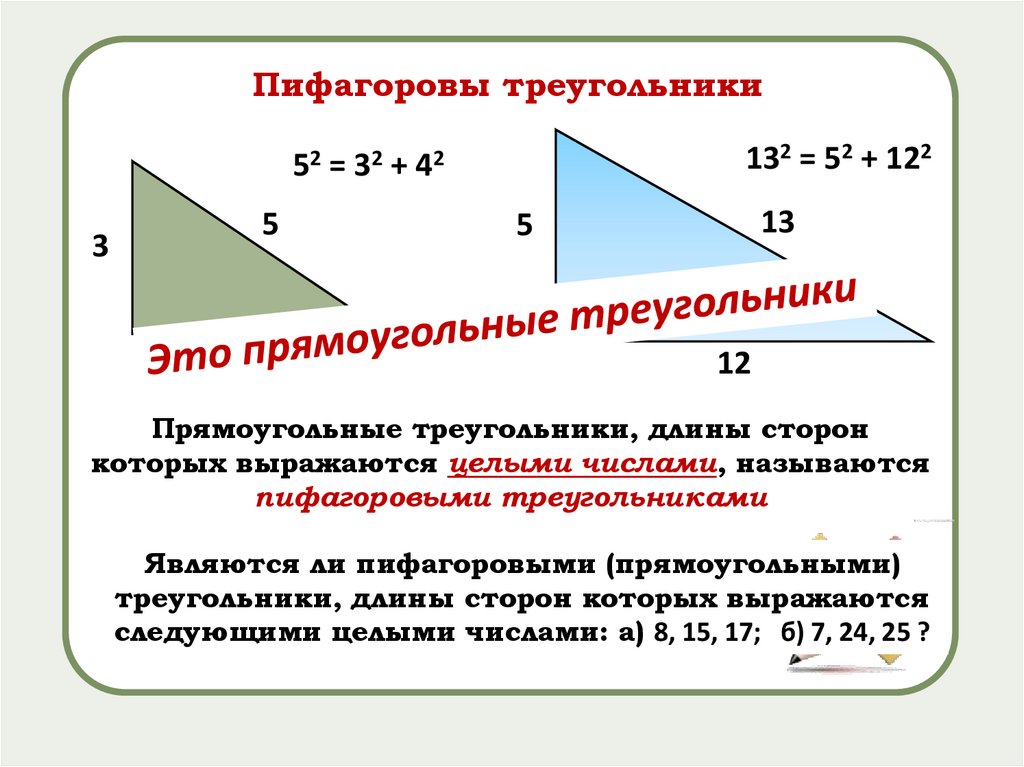
Пифагоровы треугольники132 = 52 + 122
52 = 32 + 42
5
3
4
13
5
12
Прямоугольные треугольники, длины сторон
которых выражаются целыми числами, называются
пифагоровыми треугольниками
Являются ли пифагоровыми (прямоугольными)
треугольники, длины сторон которых выражаются
следующими целыми числами: а) 8, 15, 17; б) 7, 24, 25 ?
17.
Египетский треугольник5
4
3
Крупнейший
немецкий
историк
математики Кантор (1829 - 1920 гг.)
считал, что равенство
32 + 42 = 52 было
известно уже египтянам еще около 2300 г.
до н. э., во времена царя Аменемхета I
(согласно
папирусу
6619
Берлинского
музея).
Древнегреческие
авторы
писали о существовании в
Египте особого метода для
построения прямого угла на
местности:
этому
служила
кольцевая веревка, на которой
были отмечены 12 узелко
в на равных расстояниях.
18.
Теорема Пифагора в древнем ВавилонеВавилонянам были известны многие «пифагоровы
тройки» целых чисел, удовлетворяющих равенству
x2 + y2 = z2, в том числе совсем нетривиальные
(например, 72, 65, 97 или 3456, 3367, 4825). К
сожалению, мы ничего не знаем о том, каким
методом были найдены эти числа
Задача.
Определить
длину шеста, который
вначале
вертикально
прислонен к стене, а
затем наклоняется так,
что его верхний конец
опускается
на
три
локтя,
а
нижний
отходит от стены на 6
локтей.
19.
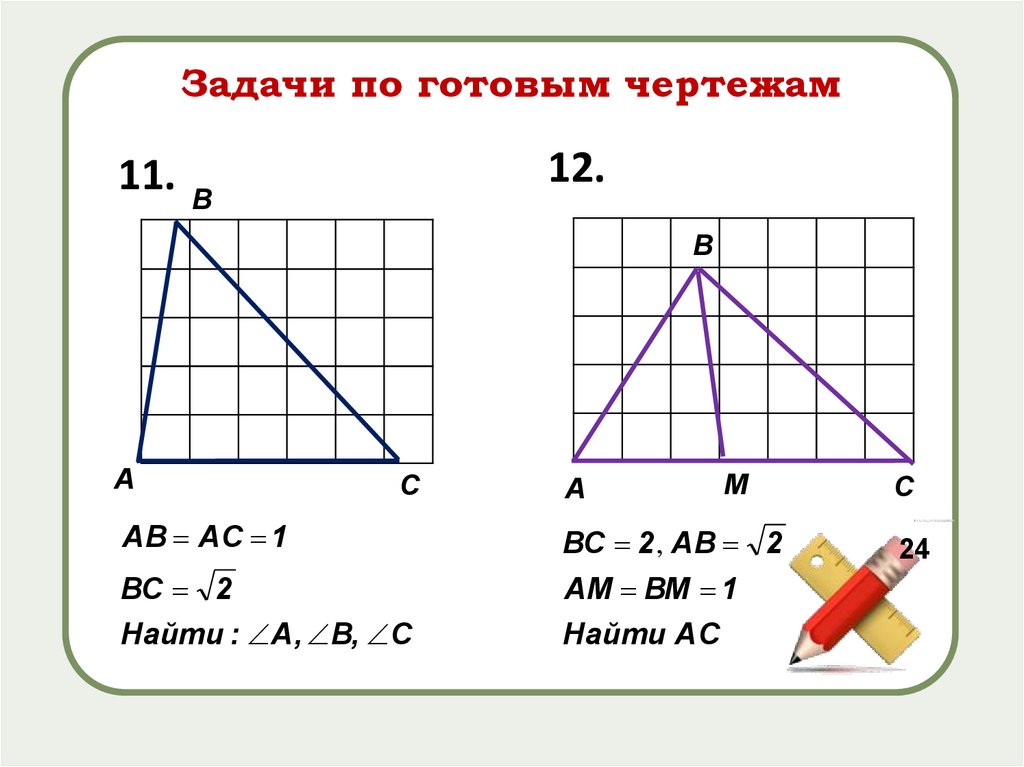
Задачи по готовым чертежам12.
11. В
В
А
С
АВ AC 1
ВС 2
Найти : А, В, С
А
М
ВС 2 , АВ 2
АМ ВМ 1
Найти АС
С
24
20.
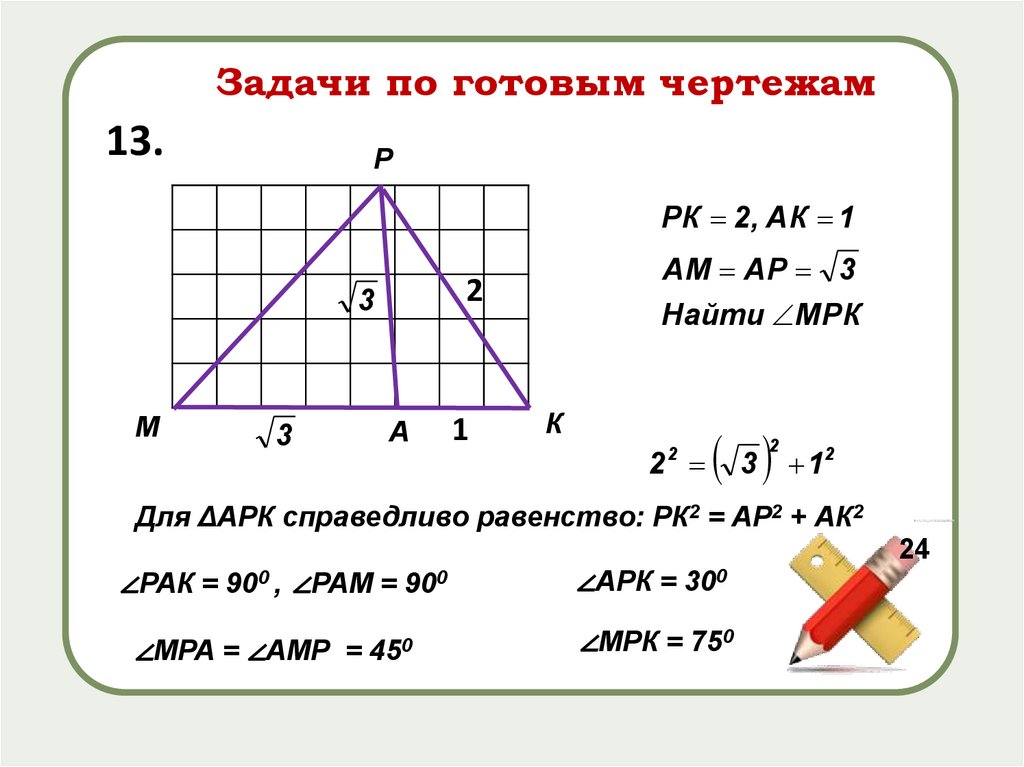
Задачи по готовым чертежам13.
Р
РК 2, АК 1
3
М
3
АМ АР 3
Найти МРК
2
А
1
К
2
2
3 1
2
2
Для ΔАРК справедливо равенство: РК2 = АР2 + АК2
24
∠РАК = 900 , ∠РАМ = 900
∠АРК = 300
∠МРА = ∠АМР = 450
∠МРК = 750
21.
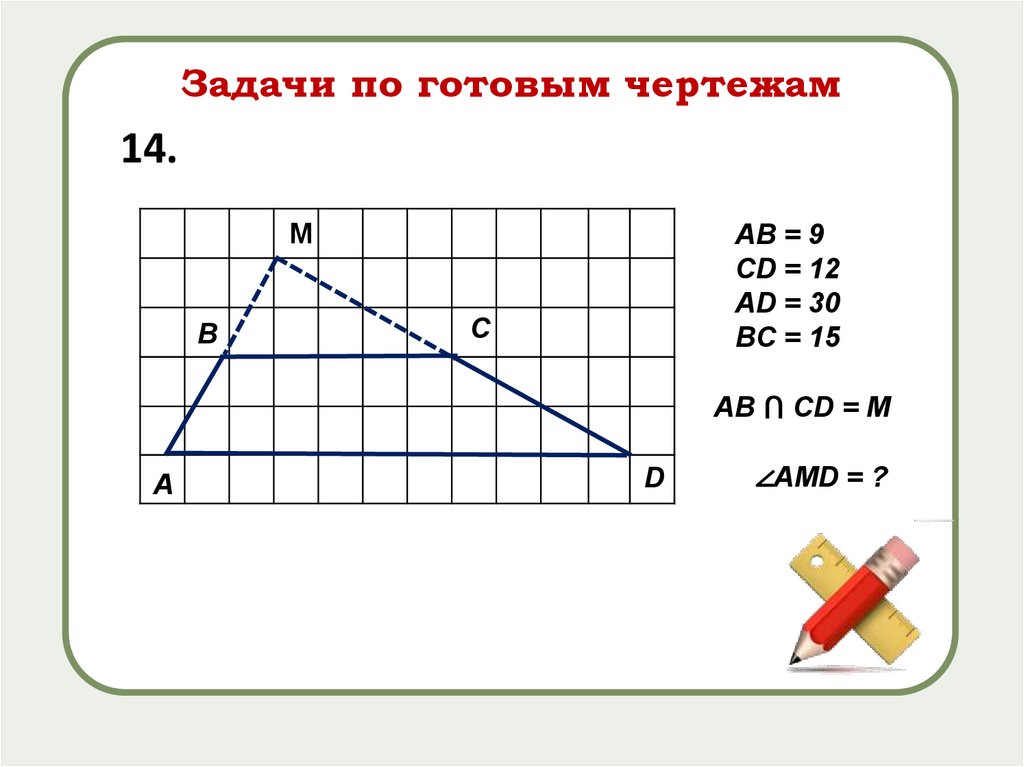
Задачи по готовым чертежам14.
M
В
AB = 9
CD = 12
AD = 30
BC = 15
С
AB ⋂ CD = M
А
D
∠AMD = ?
22.
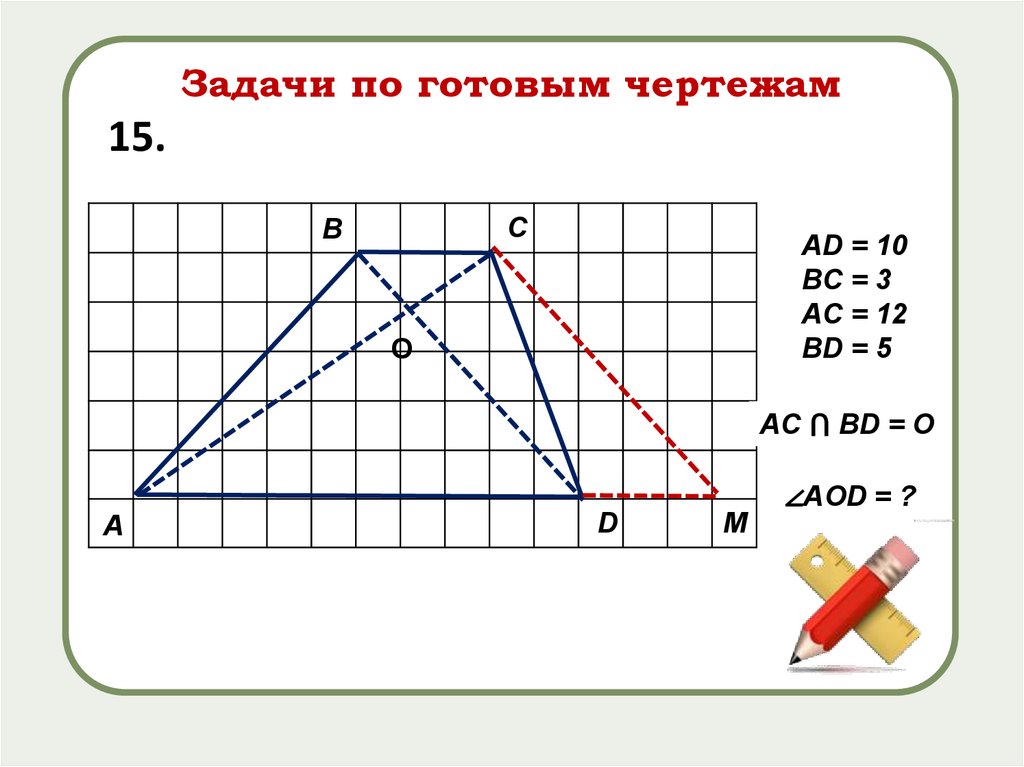
Задачи по готовым чертежам15.
С
В
AD = 10
BC = 3
AС = 12
ВD = 5
О
AС ⋂ ВD = О
А
D
М
∠AОD = ?







 mathematics
mathematics








