Теорема Пифагора

1. Ответьте на вопросы:

Площадь каких фигур мы научились
находить?
Как найти площадь следующих фигур:
- квадрата,
- прямоугольника,
- параллелограмма,
- треугольника,
- прямоугольного треугольника,
- трапеции?

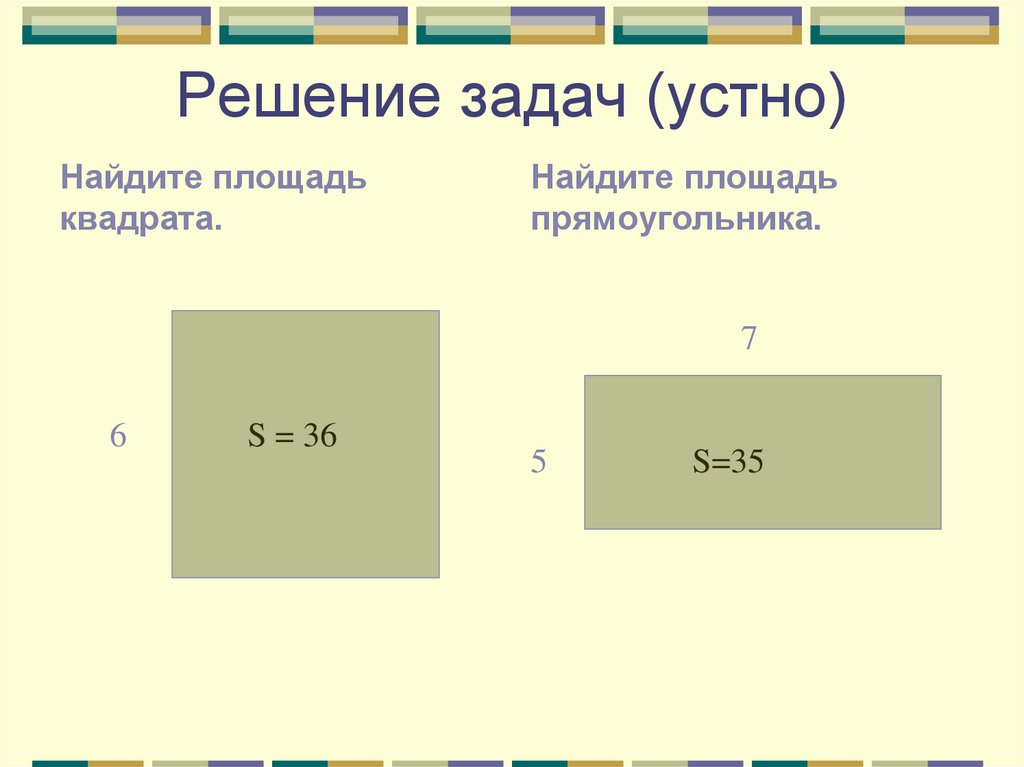
2. Решение задач (устно)

Найдите площадь
квадрата.
Найдите площадь
прямоугольника.
7
6
S = 36
5
S=35

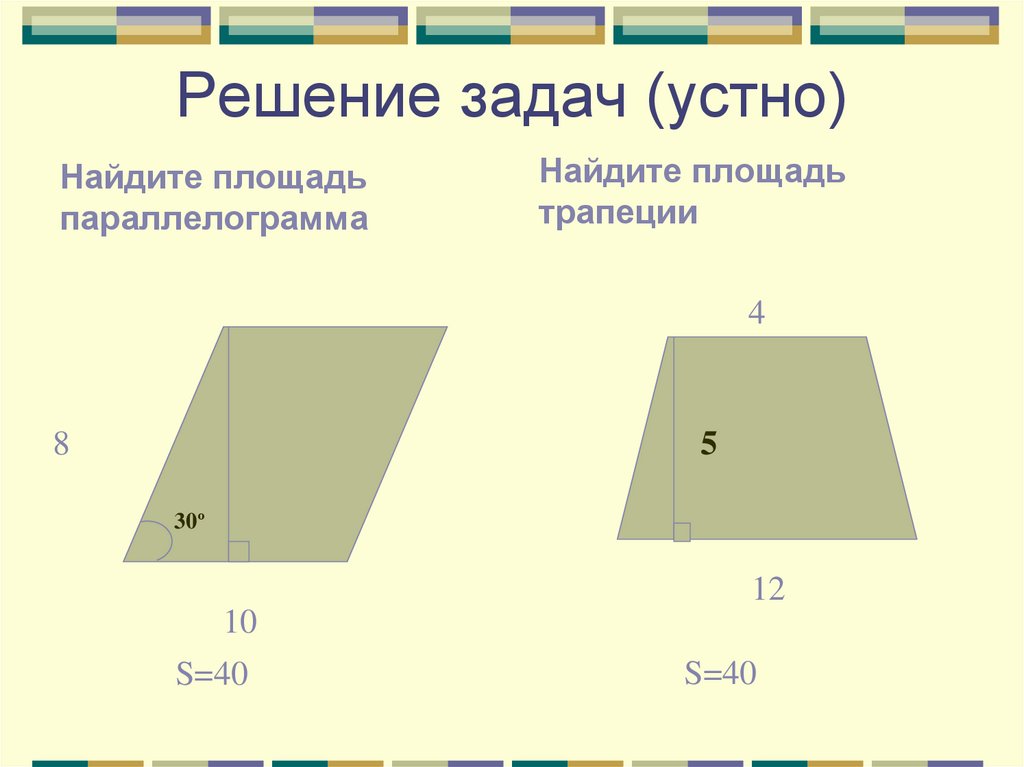
3. Решение задач (устно)

Найдите площадь
параллелограмма
Найдите площадь
трапеции
4
8
5
30º
12
10
S=40
S=40

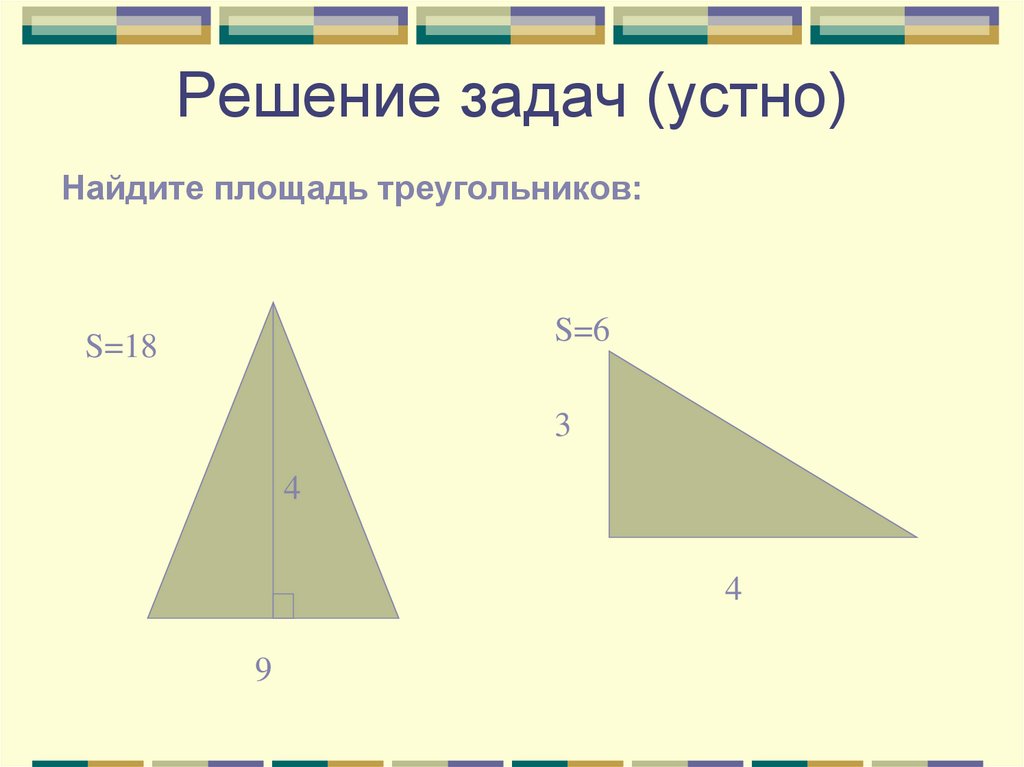
4. Решение задач (устно)

Найдите площадь треугольников:
S=6
S=18
3
4
4
9

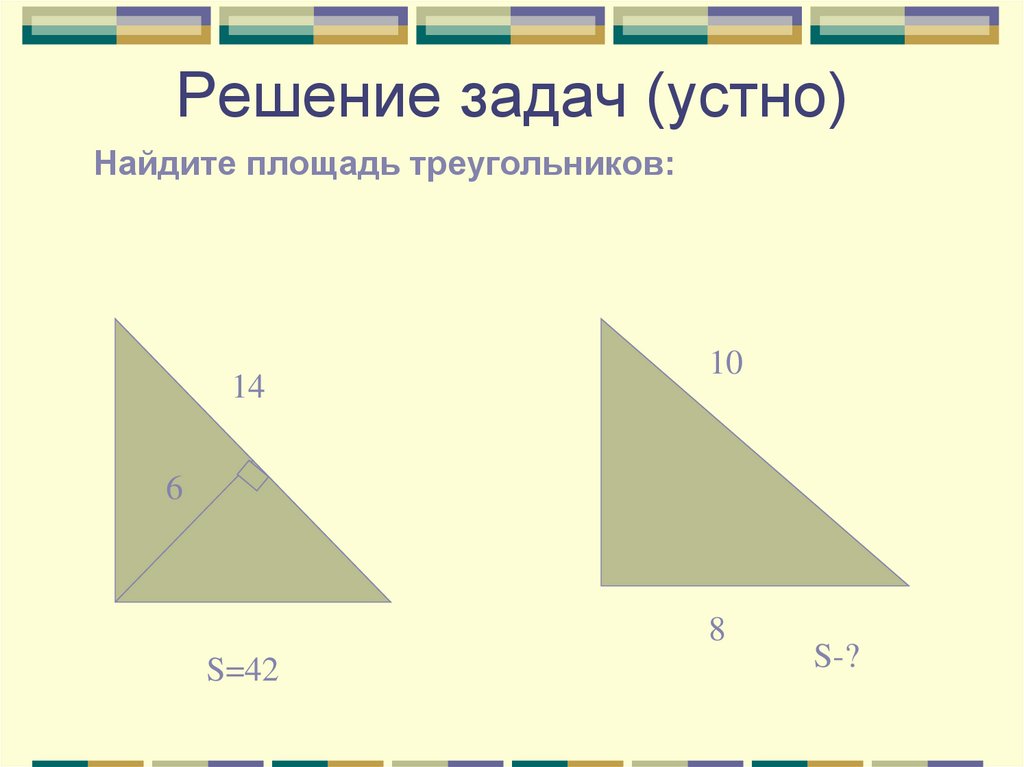
5. Решение задач (устно)

Найдите площадь треугольников:
14
10
6
8
S=42
S-?

6. Теорема Пифагора

7.

Пифагор
Существует замечательное
соотношение
между
гипотенузой и катетами
прямоугольного
треугольника,
справедливость
которого
было
доказано
древнегреческим философом
и
математиком
Пифагором(VI в до н.э.)
Не считай себя великим человеком по величине твоей тени при заходе солнца.
Пифагор.

8. Современная формулировка

« В прямоугольном треугольнике
квадрат
гипотенузы
равен
сумме квадратов катетов».

9. ТЕОРЕМА ПИФАГОРА

c
b
a

10.

ТЕОРЕМА ПИФАГОРА
c
b
a
с2 = а2 + b2

11. ТЕОРЕМА ПИФАГОРА

А
С
В

12.

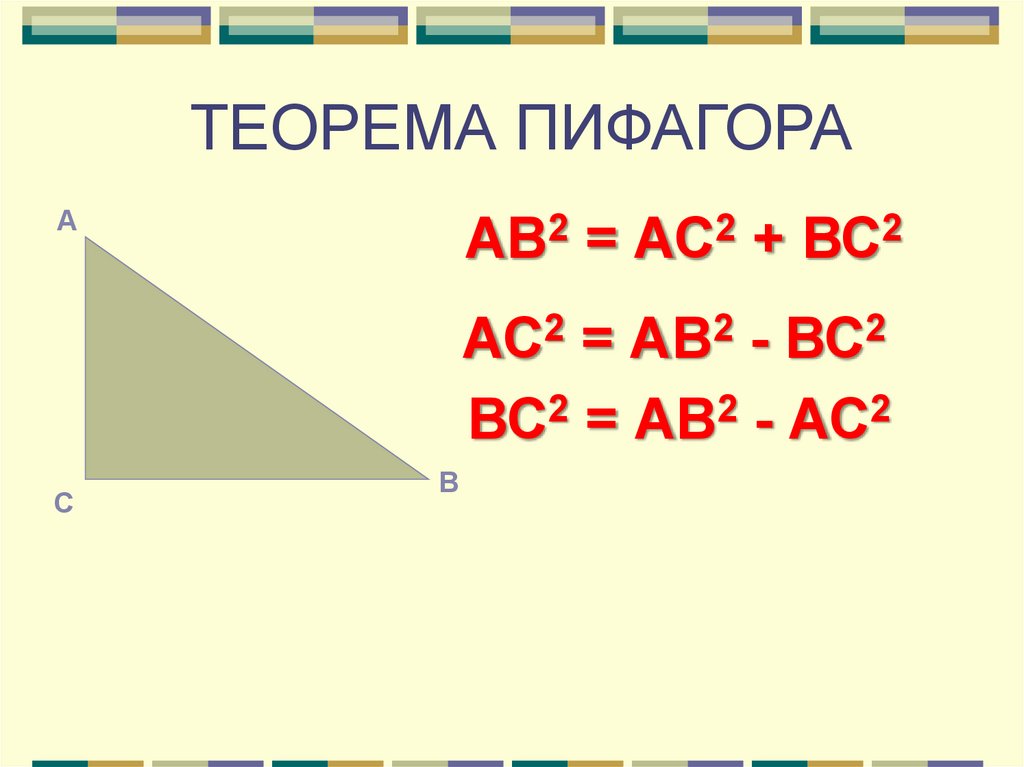
ТЕОРЕМА ПИФАГОРА
А
АВ2 = АС2 + ВС2
АС2 = АВ2 - ВС2
ВС2 = АВ2 - АС2
С
В

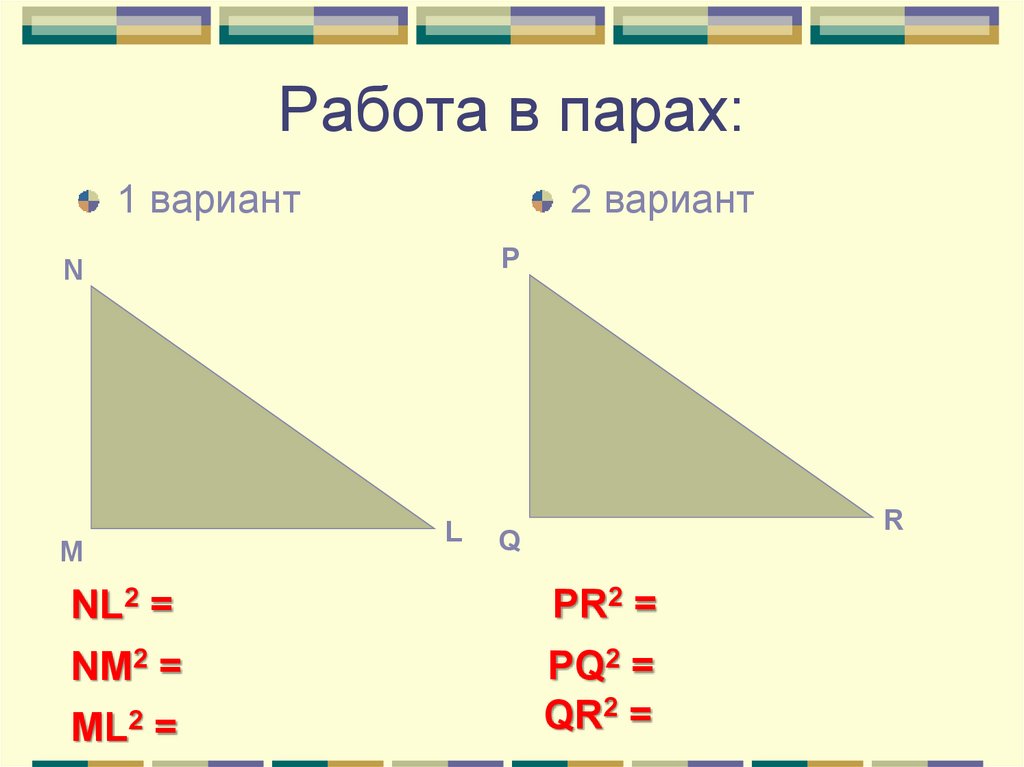
13. Работа в парах:

1 вариант
2 вариант
P
N
M
L
R
Q
NL2 =
PR2 =
NM2 =
PQ2 =
QR2 =
ML2 =

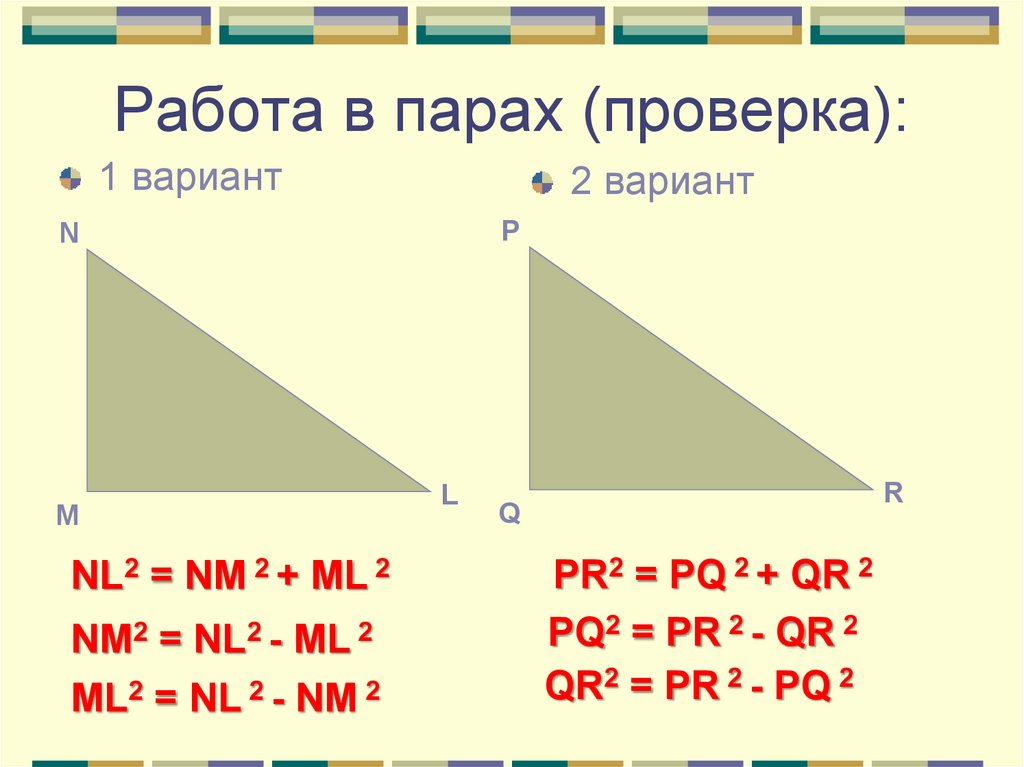
14. Работа в парах (проверка):

1 вариант
2 вариант
P
N
M
NL2 = NM 2 + ML 2
NM2 = NL2 - ML 2
ML2 = NL 2 - NM 2
L
R
Q
PR2 = PQ 2 + QR 2
PQ2 = PR 2 - QR 2
QR2 = PR 2 - PQ 2

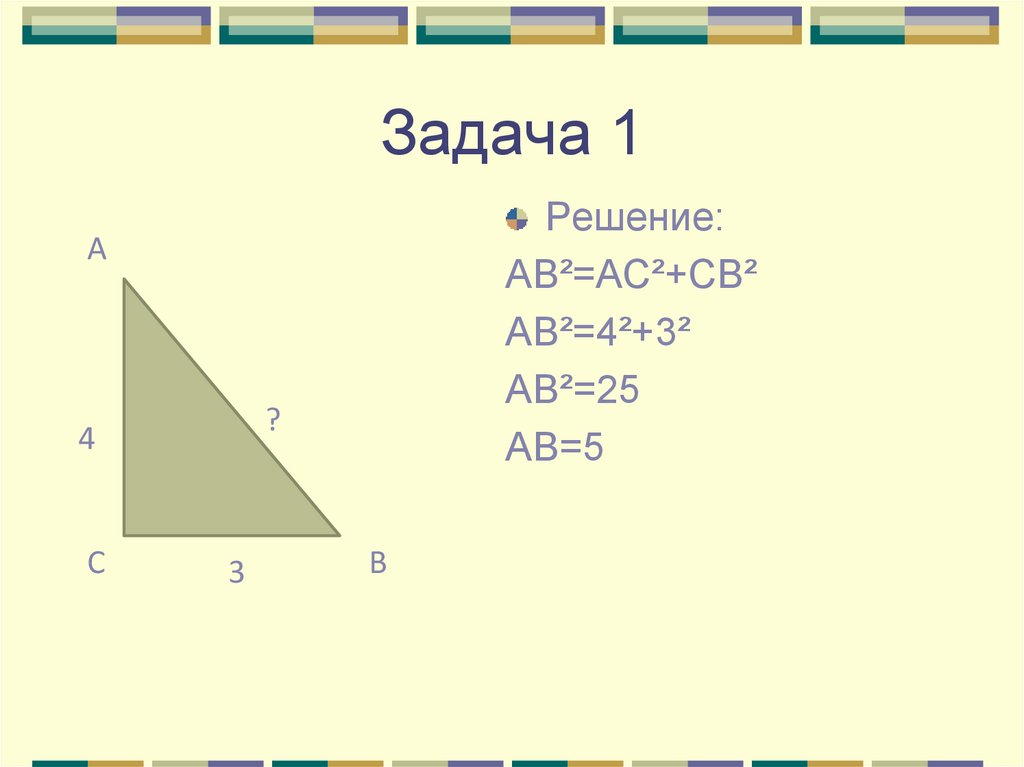
15. Задача 1

Решение:
AB²=AC²+CB²
AB²=4²+3²
AB²=25
AB=5
A
?
4
C
3
B

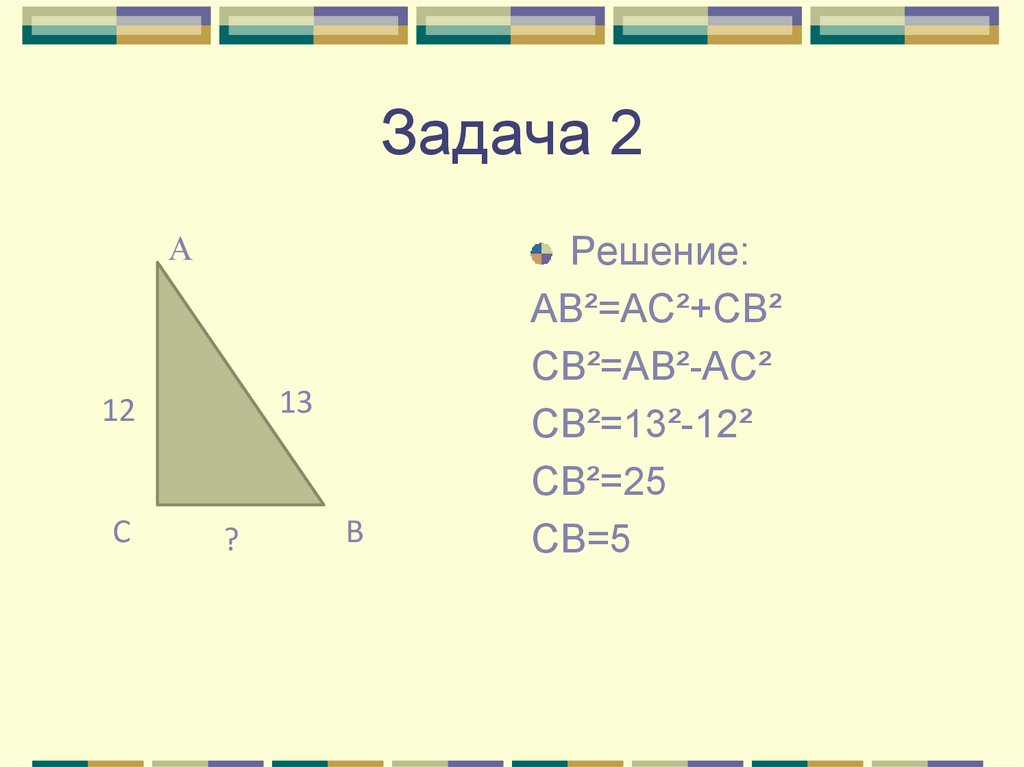
16. Задача 2

А
13
12
C
?
B
Решение:
AB²=AC²+CB²
CB²=AB²-AC²
CB²=13²-12²
CB²=25
CB=5

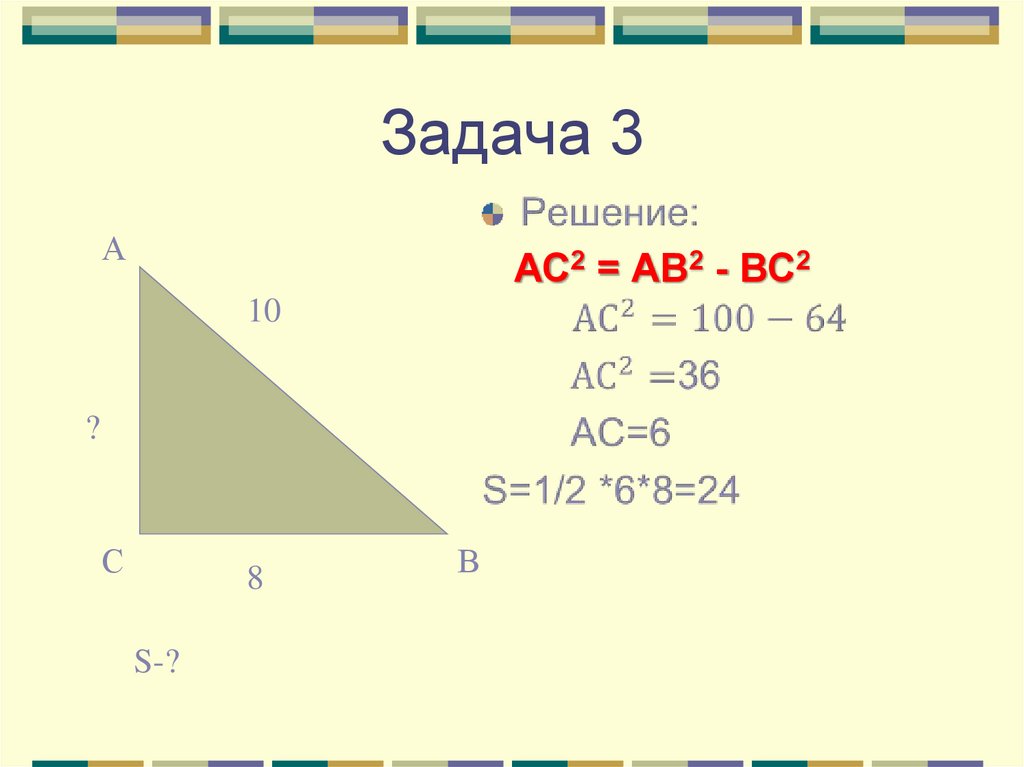
17. Задача 3

А
АС2 = АВ2 - ВС2
10
?
С
8
S-?
В

18. Итог урока:

1.
2.
Сформулируйте теорему Пифагора,
Как найти катет прямоугольного
треугольника, зная гипотенузу и
другой катет.

19. Домашнее задание

П. 54-читать, теорему выучить,
рассмотреть другие способы
доказательства теоремы
№486(в),№483(в,г),№484(в,г,д)

20. Итоги урока

Я понял теорему, могу применить для
решения задач и объяснить другому
зеленый лист
Я понял теорему, могу применить для
решения задач желтый лист
Я понял теорему, не всегда могу
применить для решения задач
голубой лист
Я ни чего не понял красный лист

21.

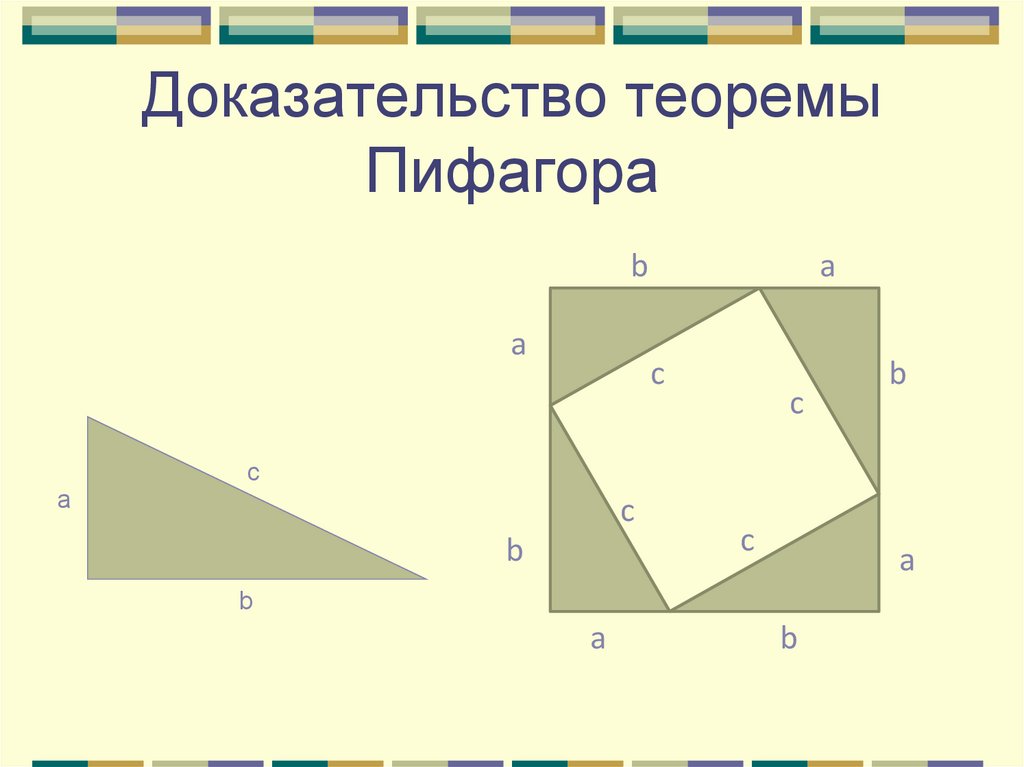
Спасибо за урок!

22. Доказательство теоремы Пифагора

b
a
a
c
c
b
c
a
c
b
c
a
b
a
b

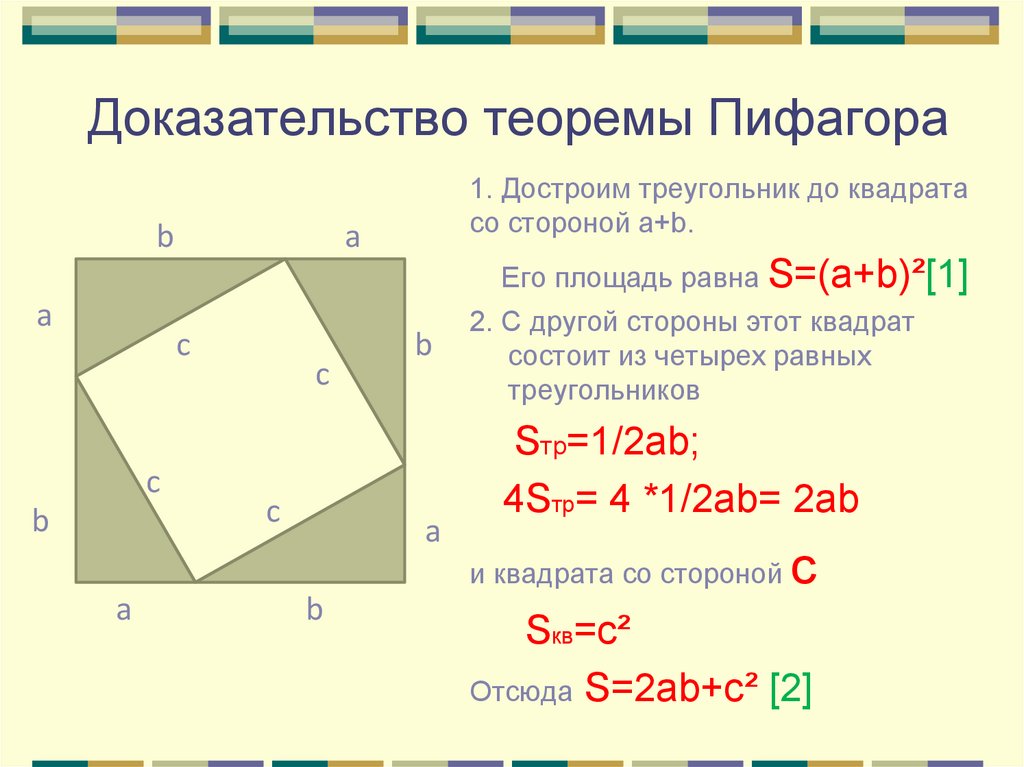
23. Доказательство теоремы Пифагора

b
1. Достроим треугольник до квадрата
со стороной a+b.
a
Его площадь равна S=(a+b)²[1]
a
c
c
b
c
c
b
a
2. С другой стороны этот квадрат
состоит из четырех равных
треугольников
Sтр=1/2ab;
4Sтр= 4 *1/2ab= 2ab
и квадрата со стороной
a
b
с
Sкв=с²
Отсюда S=2ab+c² [2]

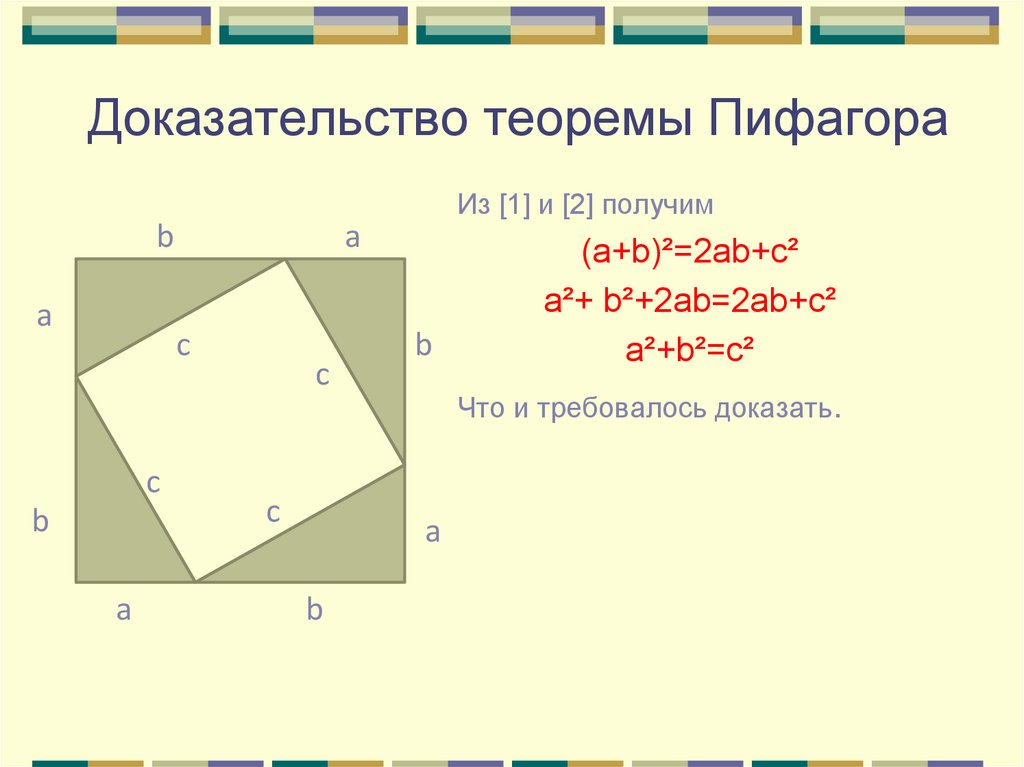
24. Доказательство теоремы Пифагора

Из [1] и [2] получим
b
a
a
c
c
b
a
c
c
b
Что и требовалось доказать.
a
b
(a+b)²=2ab+c²
a²+ b²+2ab=2ab+c²
a²+b²=c²

25. Самостоятельная работа вариант 1 вариант 2

Самостоятельная работа
вариант 1
1)
Треугольник
Найти АВ.
АВС
- прямоугольный.
вариант 2
1) Треугольник АВС – прямоугольный.
Найти СВ.
А
А
10
6
15
С
В
20
2) ABCD-прямоугольник. Найти АС.
A
С
В
2) ABCD-прямоугольник. Найти BA .
B
B
C
3
10
D
C
4
3)тр. АВС-равнобедренный,BD-высота, АСоснование. Найти АС, если BD =12, BA =13
B
A
D
C
A
D
8
3) тр. АВС-равнобедренный, BD-высота,
АС- основание. Найти АВ, если АС=20,
BD=24.
B
A
D
C

26. Решение:

Вариант 1.
1)AB²=AC²+CB²
AB²=20²+15²
AB²=625
AB=25
2)ACD-прямоуг.
AC²=AD²+DC²
AC²=4²+3²
AC²=25
AC=5
3)ABD прямоуг.
AD²=AB²-BD²
AD²=13²-12²
AD²=25
AD=5
AC=2AD=2*5=10
Вариант 2
1)AB²=AC²+CB²
BC²=AB²-AC²
BC²=10²-6²
BC²=64
BC=8
2) BAD- прямоуг.
BA²=BD²-AD²
BA²=10²-8²
BA²=36
BA=6
3)AD=½AC=10
ABD прямоуг.
AB²=AD²+BD²
AB²=10²+24²
AB²=676
AB=26