Similar presentations:
Теорема Пифагора
1. (Теорема Пифагора)
Подготовила: Чиркова
Н.В.
2. Цель урока
Познакомить учащихся:с жизнью и творчеством Пифагора;
с теоремой Пифагора.
Научить учащихся:
применять теорему Пифагора при решении задач.
Расширить знания учащихся по данной теме.
3. Ход урока
Организационный моментСтраницы из жизни Пифагора
Теорема Пифагора
Занимательная страница
Тест
Подведение итогов
Домашнее задание
4.
Пифагор – не только самый популярныйученый, но и самая загадочная личность,
человек-символ, философ, пророк.
Подлинную картину его жизни и
достижений восстановить трудно, так как
письменных документов о Пифагоре
Самосском не осталось. Известно, что
Пифагор родился на острове Самос в
Эгейском море у берегов малой Азии около
570 г. до н. э. По многим античным
свидетельствам родившийся мальчик был
сказочно красив, а вскоре проявил и
незаурядные способности. Увлекался
музыкой и поэзией. Неугомонному
воображению Пифагора очень скоро стало
тесно на маленьком острове. Мудрый
Ферекид – один из учителей Пифагора
однажды сказал: «Ты вырос из Самоса,
отправляйся путешествовать – только так ты
утолишь жажду познаний. Помни:
путешествие и память – суть два средства,
возвышающие человека и открывающие ему
врата мудрости».
5.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства,тайного монашеского ордена, члены которого обязывались вести
«пифагорейский образ жизни». Это был одновременно и религиозный
союз, и политический клуб, и научное общество. Не только сила личности
и мудрость Пифагора, но и высокая нравственность проповедуемых им
идей и жизненных принципов притягивала к нему единомышленников.
Поначалу именно талант политического оратора и религиозного
проповедника, а не мудрость философа и, тем более, естествоиспытателя,
принесли Пифагору успех. Нравственные принципы и правила,
проповедуемые Пифагором, и сегодня достойны подражания. Для всех
было у него одно правило: беги от всякой хитрости; отсекай огнем,
железом и любым оружием от тела болезнь, от души – невежество, от
утробы – роскошь, от города – смуту, от семьи – ссору. Есть две поры,
учил Пифагор, наиболее подходящие для размышления, – когда идешь ко
сну и когда пробуждаешься ото сна. День пифагорейцу надлежало
закончить стихами: «Не допускай ленивого сна на усталые очи, прежде
чем на три вопроса о деле дневном не ответишь: «Что я сделал? Что не
сделал? И что мне осталось сделать?», и начинать день со стихов:
«Прежде чем встать от сладостных снов, навеваемых ночью, душой
раскинь, какие дела тебе день приготовил».
6.
Существует замечательноесоотношение между
гипотенузой и катетами
прямоугольного
треугольника. Изучение
вавилонских клинописных
таблиц и древних китайских
рукописей показало, что это
утверждение было известно
задолго до Пифагора.
Заслуга же Пифагора
состояла в том, что он
открыл доказательство этой
теоремы.
7.
АВ
С
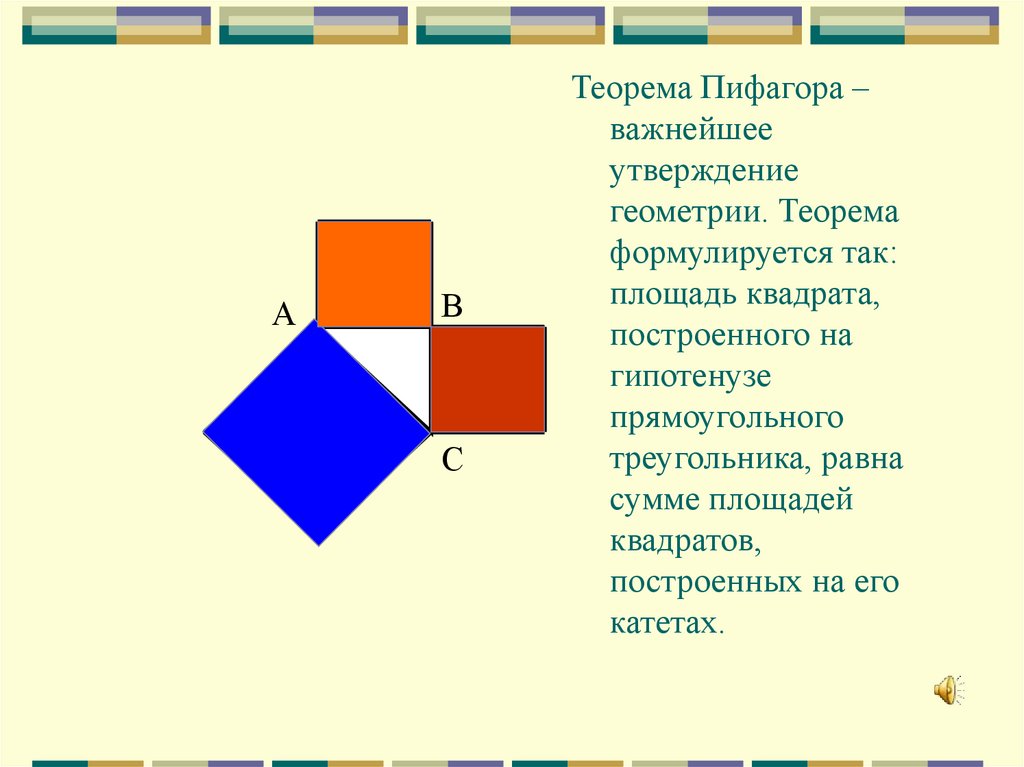
Теорема Пифагора –
важнейшее
утверждение
геометрии. Теорема
формулируется так:
площадь квадрата,
построенного на
гипотенузе
прямоугольного
треугольника, равна
сумме площадей
квадратов,
построенных на его
катетах.
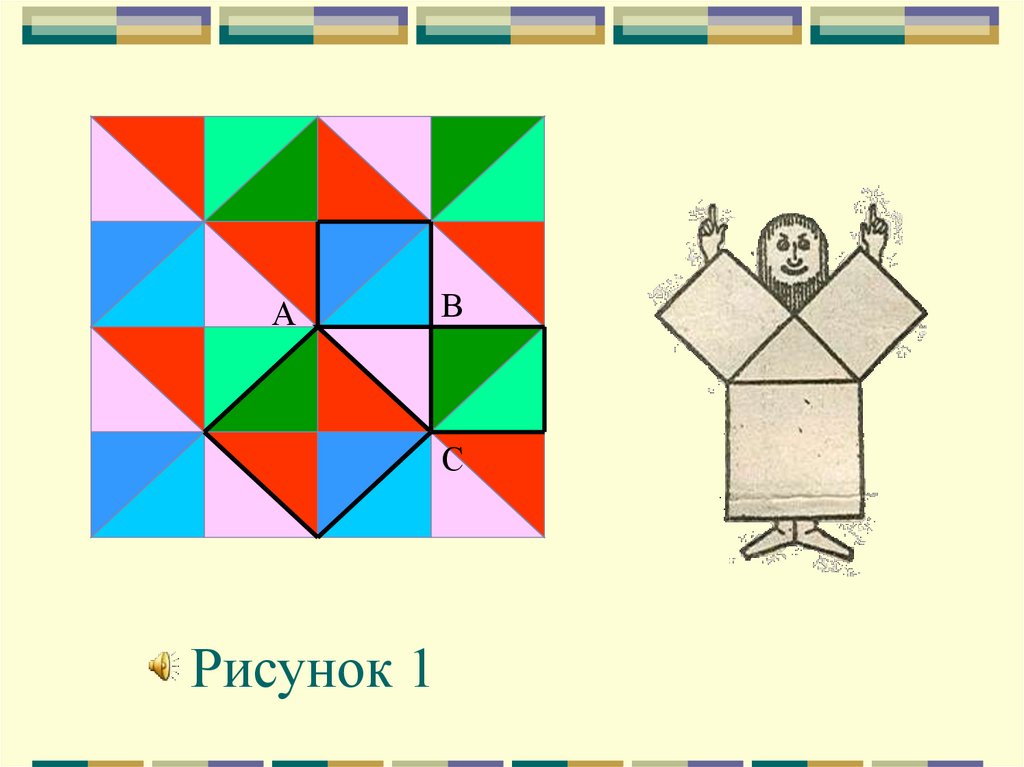
8.
АВ
С
Рисунок 1
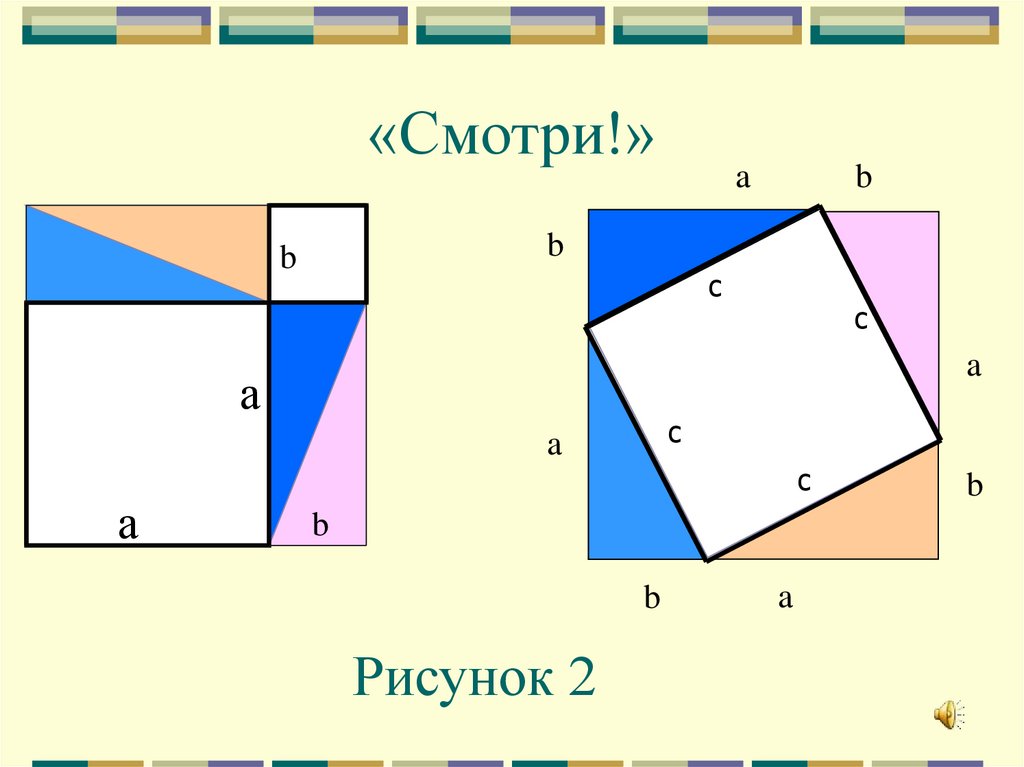
9. «Смотри!»
bb
b
c
c
a
а
c
a
а
a
c
b
b
Рисунок 2
a
b
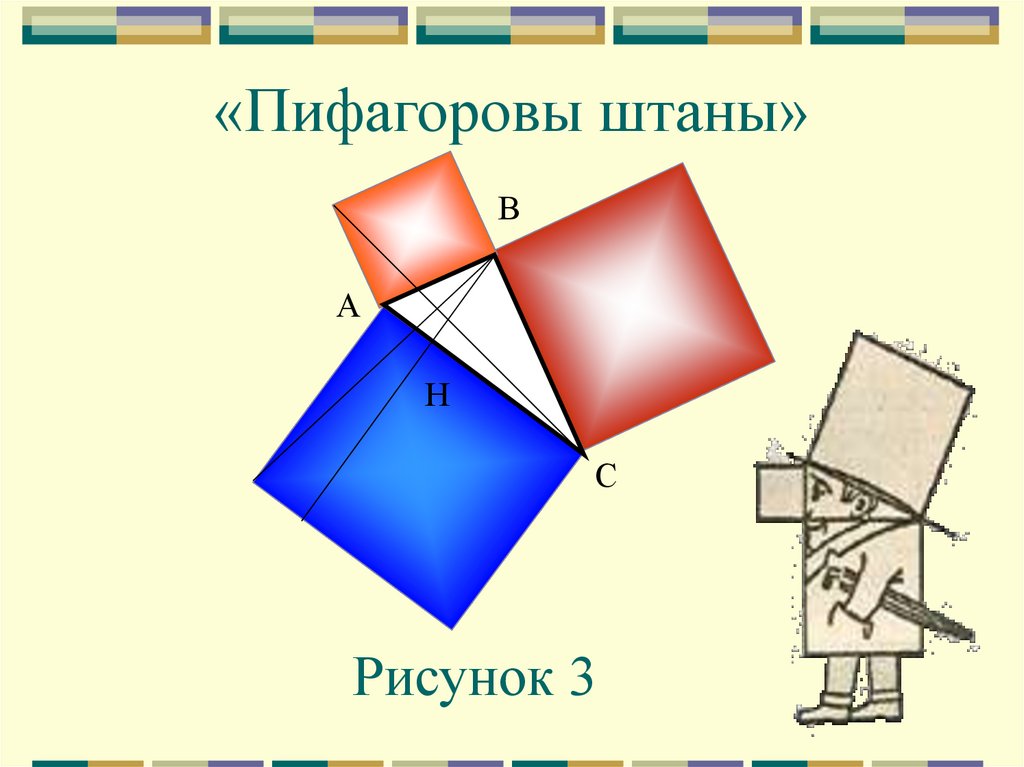
10. «Пифагоровы штаны»
ВА
Н
С
Рисунок 3
11. Прямоугольный треугольник
Аc
b
С
a
1. Какой треугольник
называется прямоугольным?
2. Как называются стороны
прямоугольного треугольника?
3. Перечислите его свойства.
4. Признаки равенства
прямоугольных треугольников.
5. Как вычисляется площадь
прямоугольного треугольника?
В
12. Теорема Пифагора (современная трактовка)
Квадрат гипотенузыравен сумме квадратов катетов
c
a
b
a2+b2=c2
13.
Выполнимдополнительные
построения
a
c
b
14.
ab
b
c
a
c
c
b
c
b
a
a
15.
ab
b
c
Это квадрат
a
Его
c площадь равна
c
a
( a + b )2
b
c
b
a
16.
ab
b
c
Это тоже квадрат
a
c
c
Его площадь равна
с2
c
b
a
a
b
17.
ab
b
a
c
Площадь этого
cтреугольникаc
1/2ab
c
b
a
a
b
18.
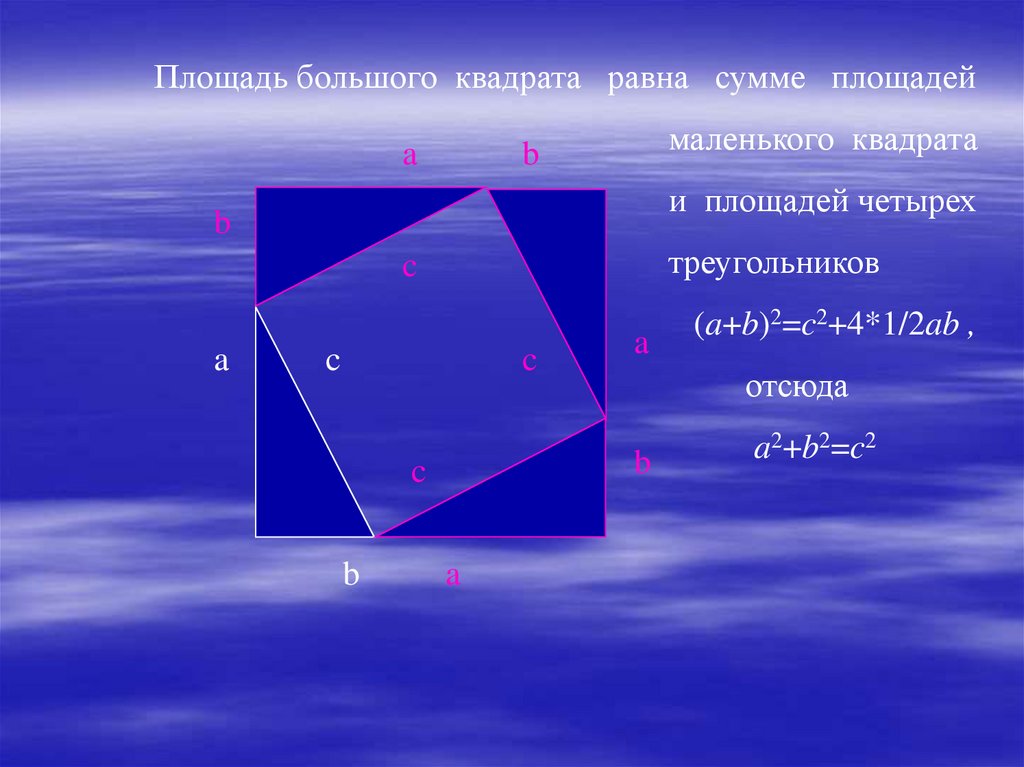
Площадь большого квадрата равна сумме площадейa
маленького квадрата
b
и площадей четырех
b
треугольников
c
a
c
c
отсюда
b
c
b
a
a
(a+b)2=c2+4*1/2ab ,
a2+b2=c2
19. Задача индийского ученого Бхаскара Акариа, 1114 г. На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его
Задача индийского ученого Бхаскара Акариа, 1114 г.На берегу ручья, ширина которого 4 фута, рос тополь.
Порыв ветра сломил его на высоте в 3 фута от земли так,
что верхний конец его коснулся другого берега ручья
(ствол направлен перпендикулярно течению).
Определить высоту тополя.
Решение.
1) AB2 = AC2 + BC2, AB = 5,
2) 5 + 3 = 8 (футов) – высота тополя.
20. Ответ: глубина озера 12 футов.
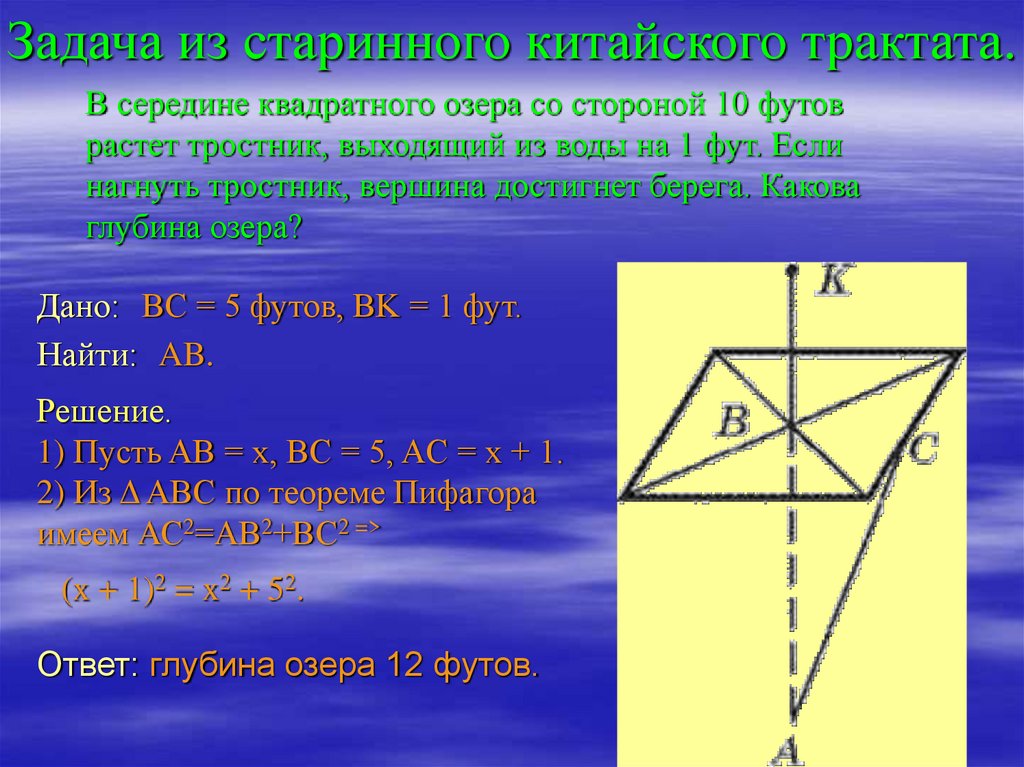
Задача из старинного китайского трактата.В середине квадратного озера со стороной 10 футов
растет тростник, выходящий из воды на 1 фут. Если
нагнуть тростник, вершина достигнет берега. Какова
глубина озера?
Дано: BC = 5 футов, BK = 1 фут.
Найти: AB.
Решение.
1) Пусть AB = x, BC = 5, AC = x + 1.
2) Из Δ ABC по теореме Пифагора
имеем АС2=АВ2+ВС2 =>
(x + 1)2 = x2 + 52.
Ответ: глубина озера 12 футов.
21.
22. I уровень 1. Укажите прямоугольный треугольник:
1)2)
3)
23. 2. Укажите гипотенузу прямоугольного треугольника:
св
а
1) а;
2) в;
3) с.
24. 3. Математическая запись теоремы Пифагора:
1) с = а + в2) с2 = а2 - в2
3) с2 = а2 + в2
25. 4. Выберите формулу квадрата суммы:
1)( а + в )2 = а2 + в2
2)
( а + в )2 = а2 + 2ав + в2
3)
( а + в )2 = а2 - 2ав + в2
26. 5. Выберите формулу площади квадрата со стороной а:
1) S = 2a2) S = 4a
3) S = a2
27. 6. Выберите формулу площади треугольника:
1) S = a + b + c2) S = a b c
3) S = a b / 2
28. II уровень
1. Найдите длину катета прямоугольноготреугольника, если другой катет и
гипотенуза равны соответственно 30 дм
и 50 дм.
1) 20дм
2) 4м
3) 10дм
4) 3м
29.
2. Найдите площадь треугольника,стороны которого равны 6см, 8см,
10см.
1) 48см
2) 9см
3) 24см2
4) 480мм
30.
3. Запишите теорему Пифагора длятреугольника АВС, у которого угол А
прямой.
1) АВ2= ВС2+АС2 2) ВС2=АС2+АВ2
3) АС2=АВ2+ВС2
4) ВС=АС- АВ
С
В
А
31. Задача для III уровня
1. В равнобедренной трапеции боковыестороны равны 13 см. Длина одного
из оснований 10 см, а второго 20 см.
Найдите площадь трапеции .
32. Подведение итогов
1. Что нового и полезного для себя вы узнали сегодня на уроке?2. В Древнем Египте был известен треугольник со сторонами 3, 4, 5; его
использовали при разметке прямоугольных земельных участков после
ежегодного уничтожения их границ разлившимся Нилом. Для построения
прямых углов египтяне поступали так: на веревке делали метки, делящие
ее на 12 равных частей, связывали концы веревки и растягивали на земле с
помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол
между сторонами, равными 3 и 4, оказывался прямым.
3. Занимаясь поисками треугольников, стороны которых a, b, c удовлетворяли
бы условию a2 + b2 = c2, Пифагор нашел формулы, которые в современной
символике могут быть записаны так:
a = 2n + 1, b = 2n(n + 1), c = 2n2 + 2n + 1, n Є Z.
4. Треугольник с такими сторонами является прямоугольным:
n = 1: а = 3, b = 4, с = 5 (приведите примеры самостоятельно).
5. Где применяется, по вашему, сейчас теорема Пифагора?
33. Домашнее задание.
Задача в стихах.Над озером тихим
С полфута размером, высился
лотоса цвет
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой
Нашел же рыбак его ранней
весной
В двух футах от места, где рос
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Ответ. 3,75 фута.
34. Успехов вам!
Презентацию подготовила учительматематики и информатики
МОУ «Парцинская средняя
общеобразовательная школа»
Чиркова Наталья Викторовна




























 mathematics
mathematics








