Similar presentations:
Путешествие по Древней Греции. Теорема Пифагора
1. Путешествие по Древней Греции
2.
3. Устная работа
Сторона квадрата равна а см. Найдитеего площадь.
Сторона квадрата равна (a + b). Как
найти его площадь?
Как найти площадь прямоугольного ?
Вычислите квадраты чисел: 2,5,7,9,12
Найдите квадратный корень из
36,81,144
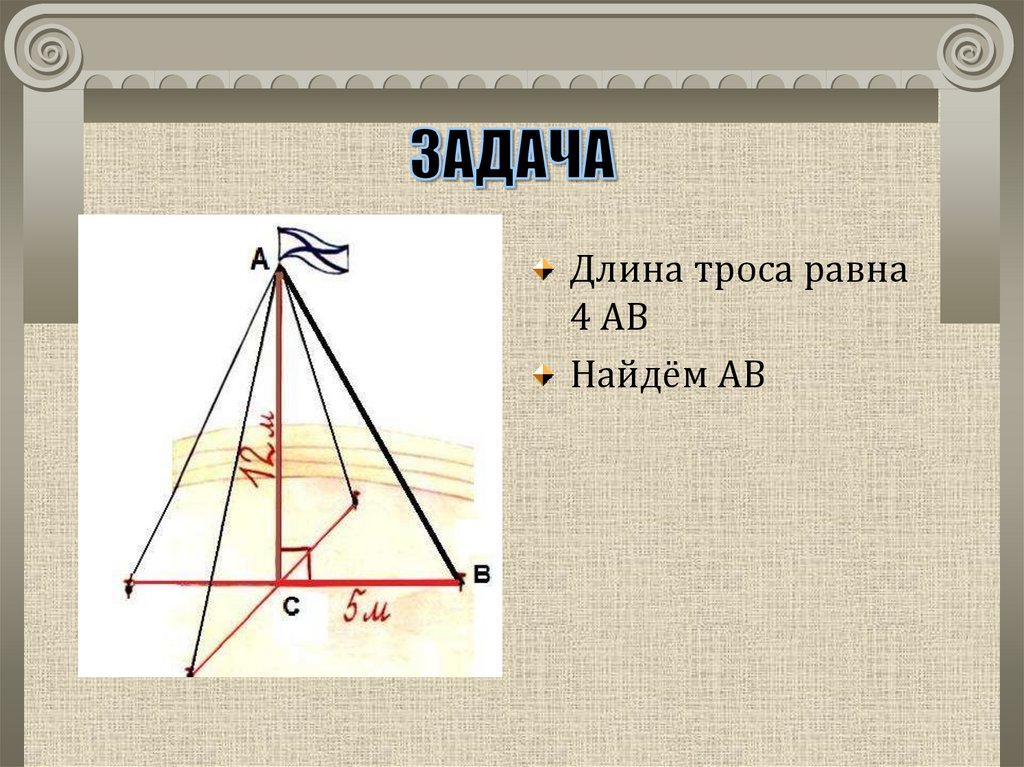
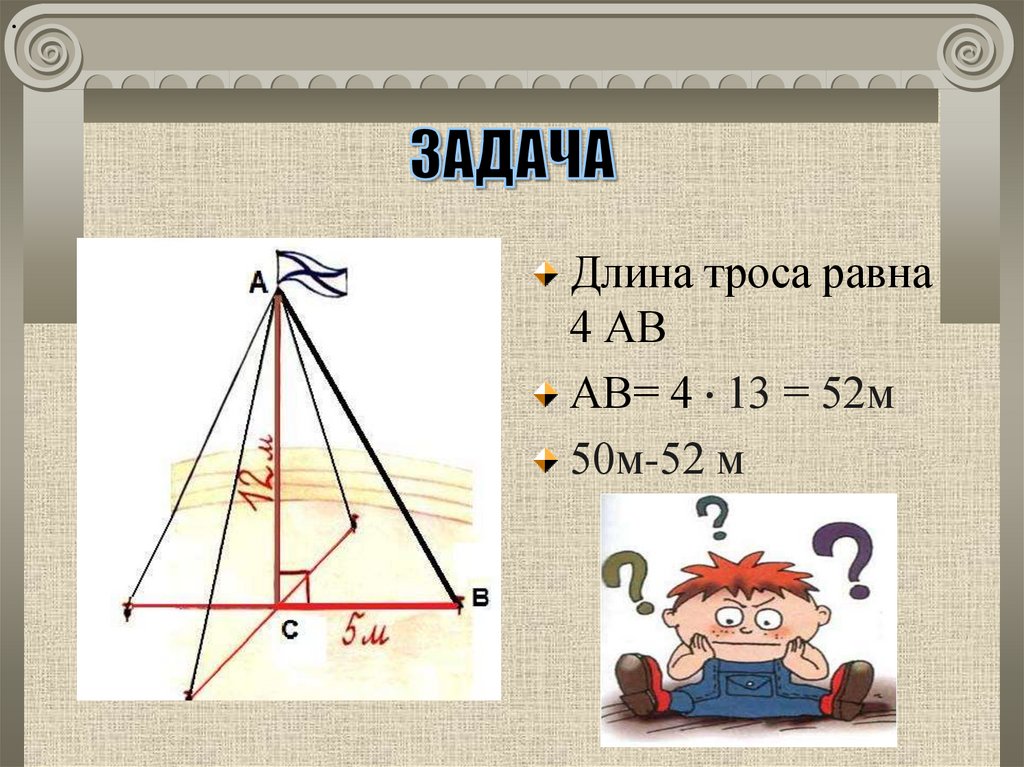
4. ЗАДАЧА
Для крепления мачты нужноустановить 4 троса. Один конец
каждого троса должен крепиться на
высоте 12 м, другой на земле на
расстоянии 5 м от мачты.
Хватит ли 50 м троса для крепления
мачты?
5.
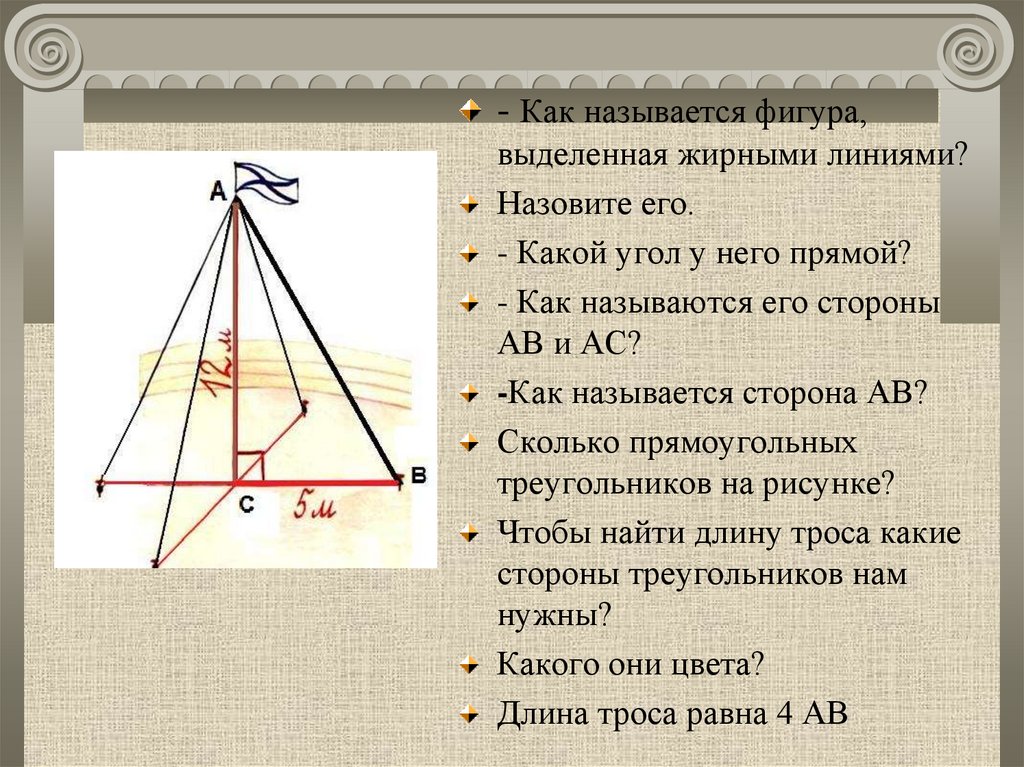
- Как называется фигура,выделенная жирными линиями?
Назовите его.
- Какой угол у него прямой?
- Как называются его стороны
АВ и АС?
-Как называется сторона АВ?
Сколько прямоугольных
треугольников на рисунке?
Чтобы найти длину троса какие
стороны треугольников нам
нужны?
Какого они цвета?
Длина троса равна 4 АВ
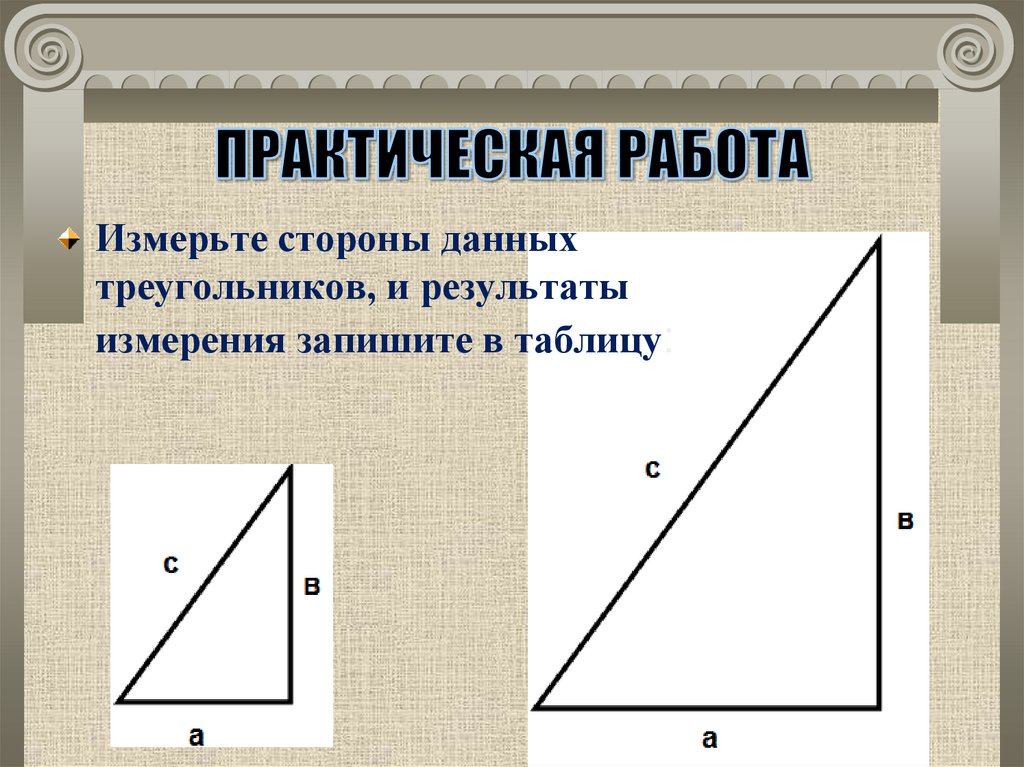
6. ПРАКТИЧЕСКАЯ РАБОТА
Измерьте стороны данныхтреугольников, и результаты
измерения запишите в таблицу:
7.
а,см
b,
см
с,
см
а2 ,
см2
b2 ,
см2
с2 ,
см2
Выполните анализ данных таблицы.
Выскажите гипотезу.
Убедитесь в своей правоте или опровергните
гипотезу, построив в тетради прямоугольный
треугольник и выполнив все необходимые
измерения и вычисления.
Запишите ваше предположение в виде формулы.
Переведите формулу на русский язык, используя
слова «квадрат», «гипотенуза», «катет», «сумма»,
«прямоугольный треугольник».
8.
а,см
b,
см
с,
см
а2 ,
см2
b2 ,
см2
с2 ,
см2
3
6
4
8
5
10
9
36
16
64
25
100
2
2
2
a +b =c
9. Пифагор Самосский. (Pythagoras of Samos)
Пифагор Самосский.(Pythagoras of Samos)
Родился: около 569
г. до РХ на острове
Самос в
Ионическом море
(Ionii).
Умер: около 475 г. до
РХ.
10. Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
построение правильных многоугольников и делениеплоскости на некоторые из них;
теорема о сумме внутренних углов треугольника;
геометрические способы решения квадратных
уравнений;
деление чисел на чётные и нечётные, простые и
составные; введение фигурных, совершенных и
дружественных чисел;
доказательство того, что не является рациональным
числом;
создание математической теории музыки и учения
об арифметических, геометрических и
гармонических пропорциях и многое другое.
11.
Пифагор первым определил и изучилвзаимосвязь музыки и математики.
Пифагор рассматривал геометрию не как практическую и
прикладную дисциплину, а как логическую науку.
Система морально-этических правил, завещанная
Пифагором, была собрана в своеобразный моральный кодекс
пифагорейцев «Золотые стихи».
Во Франции и некоторых областях Германии в
Средневековье теорему Пифагора называли «Мостом слов»,
а у математиков арабского Востока – «Теоремой невесты».
12. Теорема Пифагора: Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
его катетах.( старое звучание)
Теорема Пифагора: В прямоугольном
треугольнике квадрат гипотенузы
равен сумме квадратов катетов.
(современная формулировка)
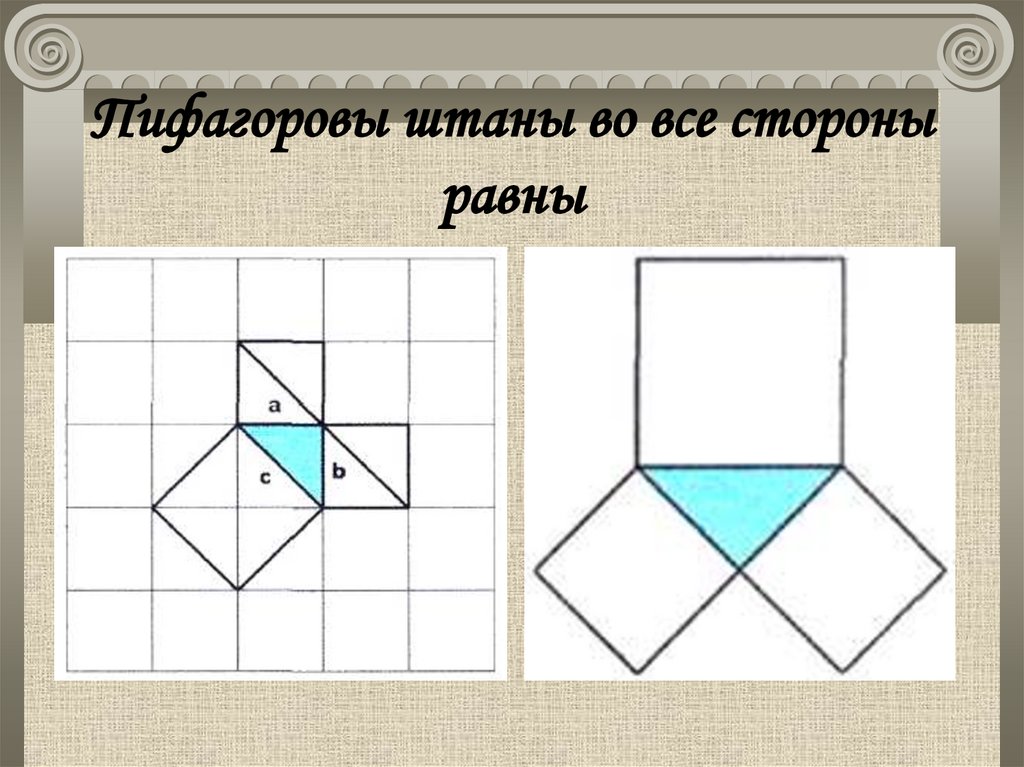
13. Пифагоровы штаны во все стороны равны
14. Шаржи
15. ТЕОРЕМА ПИФАГОРА
В прямоугольном треугольнике суммаквадратов катетов равна квадрату
гипотенузы.
Дано: прямоугольный ,
a, b – катеты,
c – гипотенуза
Док-ть: a2+b2=c2
16. ДОКАЗАТЕЛЬСТВО
1)Достроим до со стороной (a + b)2)Площадь этого квадрата (a +b)2
3)С другой стороны S = S меньшего
+4 S ( равны по двум катетам)
4)Площадь каждого = ½ab ,
5) S меньшего = с2 S большего =
можно выразить так с2 + 4·½ab.
.
6) (a+b)2 = с2 + 4·½ab
a2 + 2ab + b2 = c2 + 2ab
a2 + b2 = c2
17. Теорема Пифагора
Если дан нам треугольник,И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
И.Дырченко
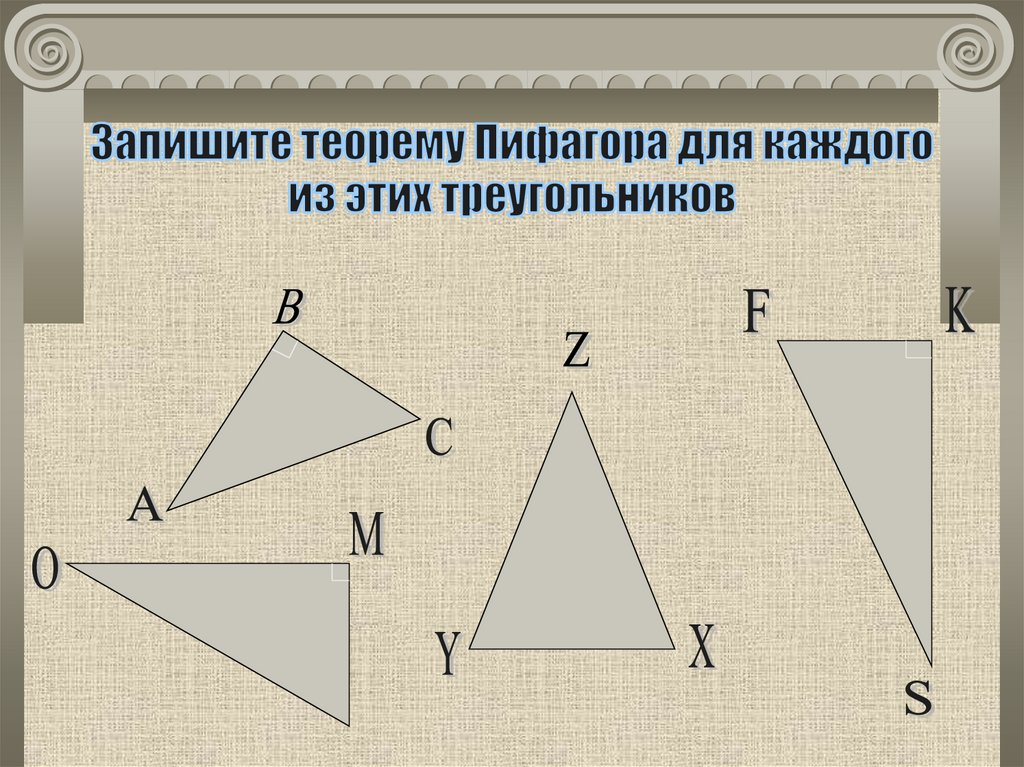
18. Запишите теорему Пифагора для каждого из этих треугольников
19. ЗАДАЧА
Длина троса равна4 АВ
Найдём АВ
20. Алгоритм решения задач с применением теоремы Пифагора
1. Указать прямоугольный треугольник;2. Записать для него теорему
Пифагора; с2 = а2+b2
3. Выразить неизвестную сторону через
две другие;
4. Подставив известные значения,
вычислить неизвестную сторону
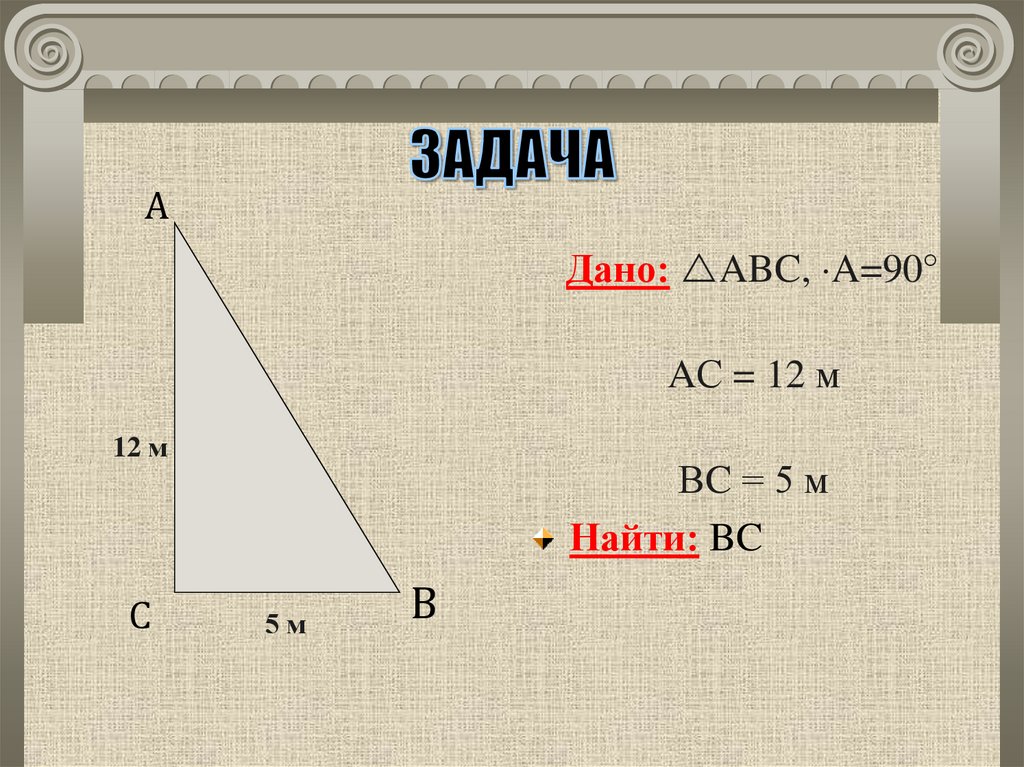
21. ЗАДАЧА
AДано: ABC, A=90°
AС = 12 м
12 м
C
ВC = 5 м
Найти: BC
5м
B
22. ЗАДАЧА
АВ =A
Решение
12 м
C
5м
АВС прямоугольный с
гипотенузой АВ, по теореме
Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 122 + 52,
АВ2 = 144 + 25,
АВ2 = 169,
АВ =
B
АВ = 13
23. ЗАДАЧА
·Длина троса равна
4 АВ
АВ= 4 · 13 = 52м
50м-52 м
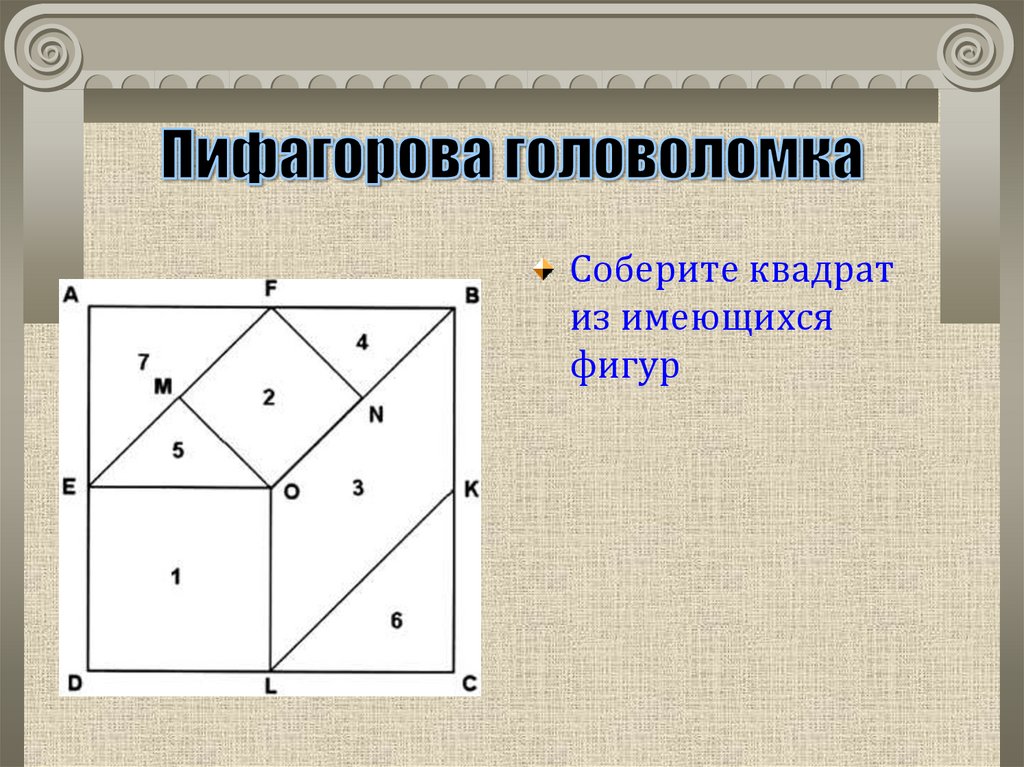
24. Пифагорова головоломка
Соберите квадратиз имеющихся
фигур
25.
Дано: прямоугольныйа и в – катеты
с – гипотенуза
а = 7, с = 9
Найти: в
Решение
с²=а²+b², а²+b²=с²,
b²=с² -а²,
b²= 92 - 72
b² =81-49
b²=36
b =6
26. ПАМЯТЬ
Памятник Пифагорунаходится в порту
города Пифагория и
напоминает всем о
теореме Пифагора,
наиболее известном его
открытии. Катет,
лежащий в основании
треугольника мраморный , гипотенуза
и фигура самого
Пифагора в виде второго
катета - медные.
27. Изречения Пифагора
Статуя формой своей хороша,А человека украсят дела.
Шуткой беседу укрась, освети.
Шутка, что соль. Лишь не пересоли…
Лучше молчи, ну, а коль говоришь,
Пусть будет лучше, чем то, что молчишь.
Если ты в гневе, не смей говорить!
Действовать резко и злобу сорить.
Пред тем, как станешь говорить, пусть мысль созреет
Под языком твоим. Созревшая - все смеет.
28. Домашнее задание
– Выучить теорему Пифагора сдоказательством
творческое задание: попробуйте
сочинить стихотворение и нарисовать
шарж, которого нет на выставке.
– Задачи из учебника № 483 б, в;
№ 484 а, в. или :
29.
12 апреля 1961 года Ю.А. Гагарин накосмическом корабле “Восток” был поднят
над землёй на максимальную высоту 327
километров. На каком расстоянии от
корабля находились в это время наиболее
удалённые от него и видимые космонавтом
участки поверхности Земли? (Радиус Земли
≈6400 км).
30. Задача индийского математика XII века Бхаскары
На берегу реки рос тополь одинокий.Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
31. Спасибо за урок
О, Мудрецы времени!Дружней вас не сыскать
Совет сегодня завершен,
но
Каждый должен знать:
Познанье, упорство, труд
К прогрессу в жизни
приведут






















 mathematics
mathematics