Сечение куба

1. “Сечение многогранника плоскостью”

Построить сечение куба ABCDA’B’C’D’
плоскостью, проходящей через
середины ребер AB, AA’, A’D’.

2.

Дано:
ABCDA’B’C’D’ - куб
B’
C’
P
A’
B
(.) P – середина A’D’.
C
Построить сечение через
точки M, N, P.
M
A
(.) N – середина AA’,
D’
N
(.) M – середина AB,
D

3.

C’
B’
(.) N принадлежит AA’D’D,
P
A’
(.) P принадлежит AA’D’D.
D’
Проведем отрезок,
соединяющий (.) N и (.) P,
N
B
C
M
A
D
лежащие в одной и той же грани.
NP принадлежит секущей
плоскости куба.

4.

B’
C’
(.) N принадлежит AA’B’B,
P
(.) M принадлежит AA’B’B.
D’
A’
Проведем отрезок,
соединяющий (.) N и (.) M,
N
B
C
M
A
D
лежащие в одной и той же
грани. NM принадлежит
секущей плоскости куба.

5.

B’
C’
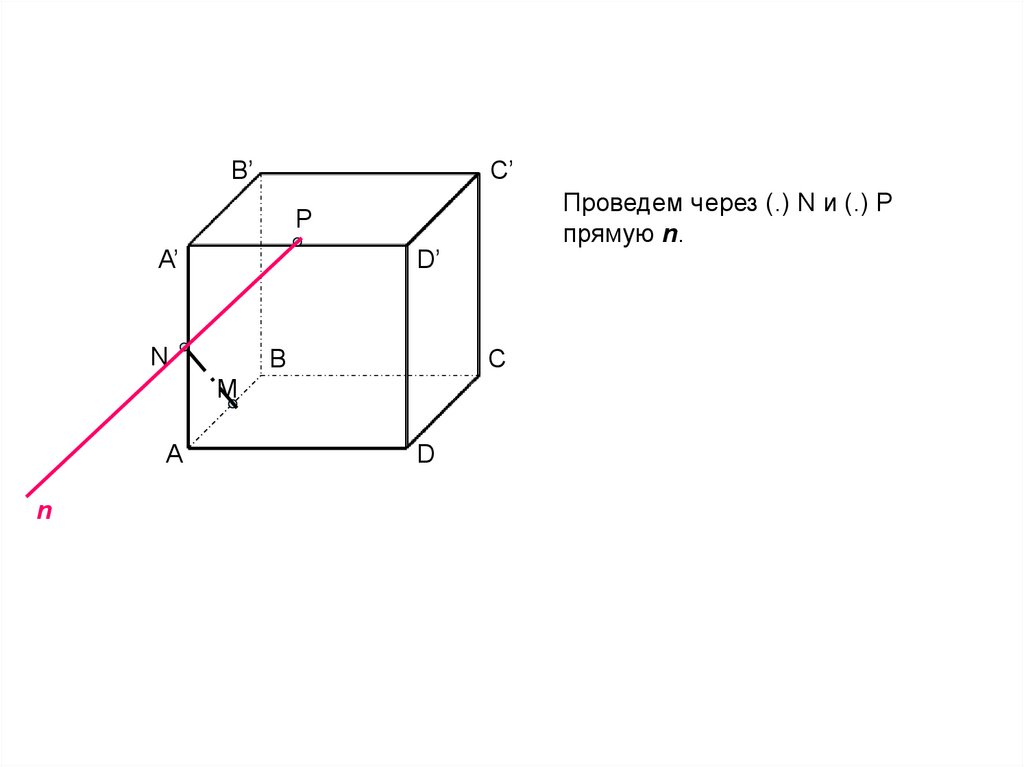
Проведем через (.) N и (.) P
прямую n.
P
A’
D’
N
B
C
M
A
n
D

6.

B’
C’
Проведем прямую m через (.)
A и (.) D. n m = X.
P
A’
D’
N
B
C
M
m
X
n
A
D

7.

C’
B’
(.) X принадлежит плоскости
основания.
P
A’
D’
k
N
B
L
C
M
m
X
n
A
D
(.) M принадлежит
основанию.
Проведем прямую k через (.)
X и (.) M.
k BC = L.
ML принадлежит секущей
плоскости куба.

8.

B’
C’
NP принадлежит AA’D’D,
P
L принадлежит BB’C’C.
D’ K
A’
k
N
B
L
C
M
m
X
n
A
D
AA’D’D BB’C’C.
Значит, через (.) L проведем
отрезок, параллельный
отрезку NP, до пересечения с
ребром CC’.
Получили (.) K.
LK принадлежит секущей
плоскости куба.

9.

C’
B’
NM принадлежит AA’B’B.
F
P
A’
(.) K принадлежит DD’C’C.
K
D’
AA’B’B DD’C’C.
k
N
B
L
C
M
m
X
n
A
D
Значит, через (.) K проведем
отрезок, параллельный
отрезку NM, до пересечения с
ребром D’C’.
Получили (.) F.
KF принадлежит секущей
плоскости куба.

10.

C’
B’
F
P
A’
K
D’
k
N
B
L
C
M
m
X
n
A
D
Проведем отрезок,
соединяющий (.) P и (.) F,
лежащие в одной и той же
грани. PF принадлежит
секущей плоскости куба.

11.

B’
C’
Отрезки NP, NM, ML, LK, KF,
PF принадлежат секущей
плоскости куба.
F
P
A’
K
D’
k
N
B
L
C
M
MNPFKL – искомое сечение.
m
X
n
Получили шестиугольник,
сторонами которого являются
эти отрезки.
A
D

12. Теоретические сведения

Секущей плоскостью многогранника называется любая плоскость, по обе
стороны от которой имеются точки данного многогранника. Секущая
плоскость пересекает грани многогранника по отрезкам. Многоугольник,
сторонами которого являются эти отрезки, называется сечением
многогранника.
Свойство параллелепипеда: Противоположные грани параллелепипеда
параллельны и равны.
При построении сечений параллелепипеда надо учитывать ,что если
секущая плоскость пересекает две противоположные грани по каким-то
отрезкам, то эти отрезки параллельны по свойству параллельных
плоскостей.
Свойство: Если две параллельные плоскости пересечены третьей, то линии
их пересечения параллельны.