Similar presentations:
Призма. Элементы призмы
1.
Призма.Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
2.
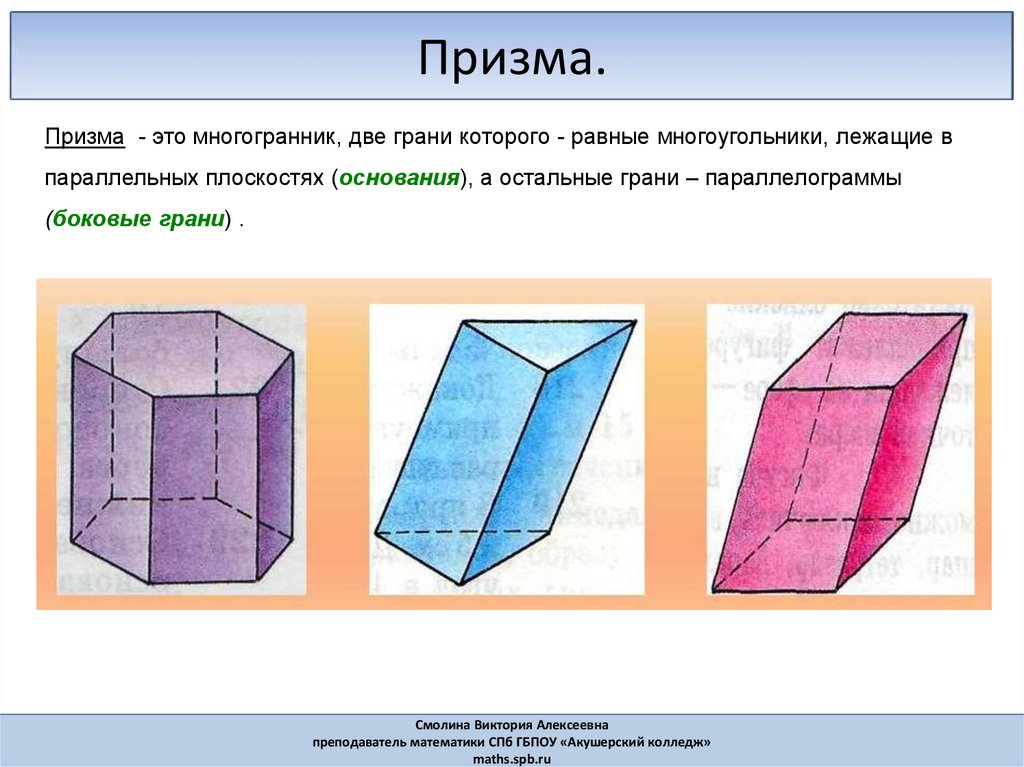
Призма.Призма - это многогранник, две грани которого - равные многоугольники, лежащие в
параллельных плоскостях (основания), а остальные грани – параллелограммы
(боковые грани) .
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
3.
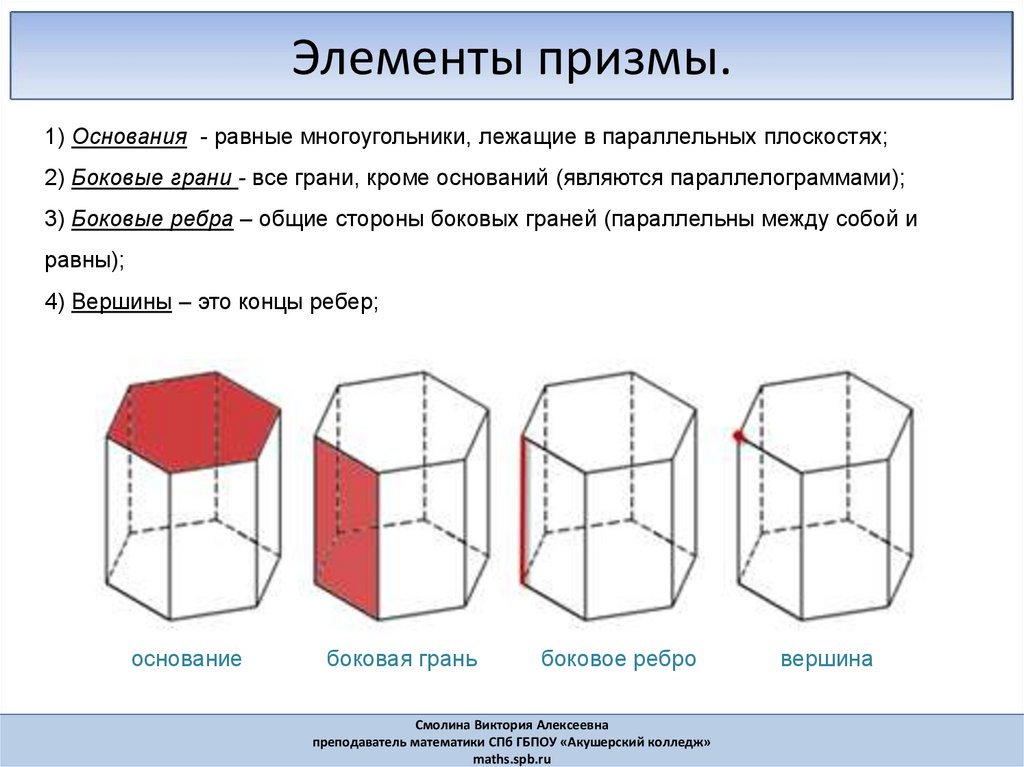
Элементы призмы.1) Основания - равные многоугольники, лежащие в параллельных плоскостях;
2) Боковые грани - все грани, кроме оснований (являются параллелограммами);
3) Боковые ребра – общие стороны боковых граней (параллельны между собой и
равны);
4) Вершины – это концы ребер;
основание
боковая грань
боковое ребро
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
вершина
4.
Элементы призмы.5) Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной
грани.
6) Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного
основания к плоскости другого основания.
диагональ
высота
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
5.
Призма бывает:и т.д.
Четырехугольная призма
Треугольная призма
Шестиугольная призма
Пятиугольная призма
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
6.
Призма бывает:Прямая призма
Наклонная призма
Боковые грани – прямоугольники.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
7.
Свойство прямой призмыРебро прямой призмы является высотой призмы.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
8.
Призма бывает правильнойПрямая призма + в основании правильный многоугольник = правильная призма
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
9.
Развертка призмы.Развертка многогранника – это плоская фигура, состоящая из всех граней многогранника.
Основания
Боковые грани
Развертка наклонной треугольной призмы.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
10.
Развертка призмы.Развертка правильной треугольной призмы.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
11.
Развертка призмы.Развертка правильной шестиугольной призмы.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
12.
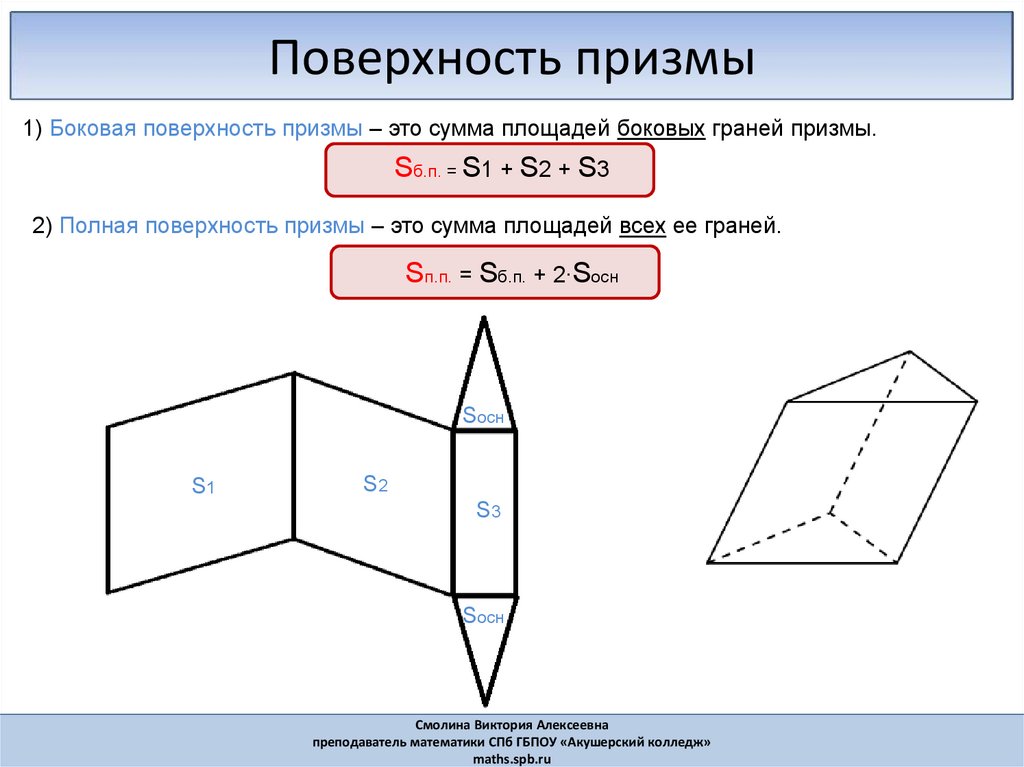
Поверхность призмы1) Боковая поверхность призмы – это сумма площадей боковых граней призмы.
Sб.п. = S1 + S2 + S3
2) Полная поверхность призмы – это сумма площадей всех ее граней.
Sп.п. = Sб.п. + 2∙Sосн
Sосн
S1
S2
S3
Sосн
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
13.
Боковая поверхность прямой призмыБоковая поверхность прямой призмы равна произведению высоты призмы на периметр
ее основания.
Sб.п. Росн h
h
Pосн
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
14.
Объем призмыОбъем любой призмы равен произведению площади основания на высоту.
V Sосн h
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
15.
Объем наклонной призмыДля вычисления объема наклонной призмы существует еще одна формула:
Объем наклонной призмы равен произведению бокового ребра на площадь
перпендикулярного к нему сечения.
A1
C1
AA1=l – боковое ребро
B1
l
S
- площадь перпендикулярного к ребру
сечения
V= S l
S
C
A
B
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
16.
Частные случаи призмы:1) Параллелепипед – это призма, основаниями которой являются
параллелограммы.
2) Прямоугольный параллелепипед – это параллелепипед, у которого
все грани – прямоугольники.
3) Куб – прямоугольный параллелепипед, у которого все три
измерения равны.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
17.
Свойства прямоугольного параллелепипеда.1) Диагонали прямоугольного параллелепипеда равны;
2) Диагонали параллелепипеда пересекаются в одной точке
и делятся этой точкой пополам.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
18.
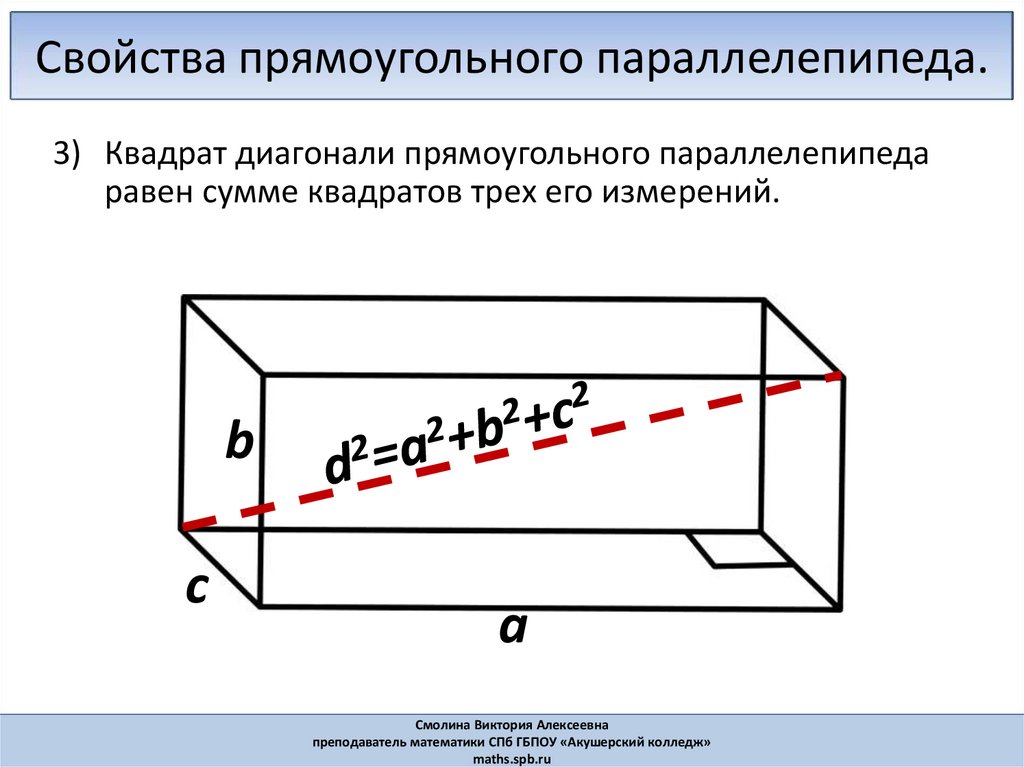
Свойства прямоугольного параллелепипеда.3) Квадрат диагонали прямоугольного параллелепипеда
равен сумме квадратов трех его измерений.
b
c
a
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
19.
Формула объема прямоугольного параллелепипеда.b
c
V a b c
a
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
20.
Формула объема куба.a
V a
a
a
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
3
21.
Упражнение.На рисунке найдите фигуры, которые являются развертками призм.
Определите вид этих призм.
1)
2)
3)
4)
7)
5)
8)
6)
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
22.
Задача 1Задача 1: Основание прямой призмы - равнобедренный
треугольник с боковой стороной 13, в котором высота
проведенная к основанию, равна 12. Найдите площадь полной
поверхности призмы, если только одна из ее боковых граней –
квадрат.
12
м
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
23.
Задача 2Задача 2:
Стороны основания прямоугольного параллелепипеда равны
12 и 5, а угол между диагональю параллелепипеда и
плоскостью основания равен 45 . Найдите диагональ
параллелепипеда, площадь боковой поверхности и объем.
ПЛАН РЕШЕНИЯ:
1. Постройте угол между
диагональю параллелепипеда и
основанием ( С1АС)
2. Найдите по т. Пифагора длину
диагоналиAC прямоугольника АВСD
3. Найдите катет С1С и длину
гипотенузы треугольника С1АС
45
4. Найдите площадь боковой
поверхности и объем.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
24.
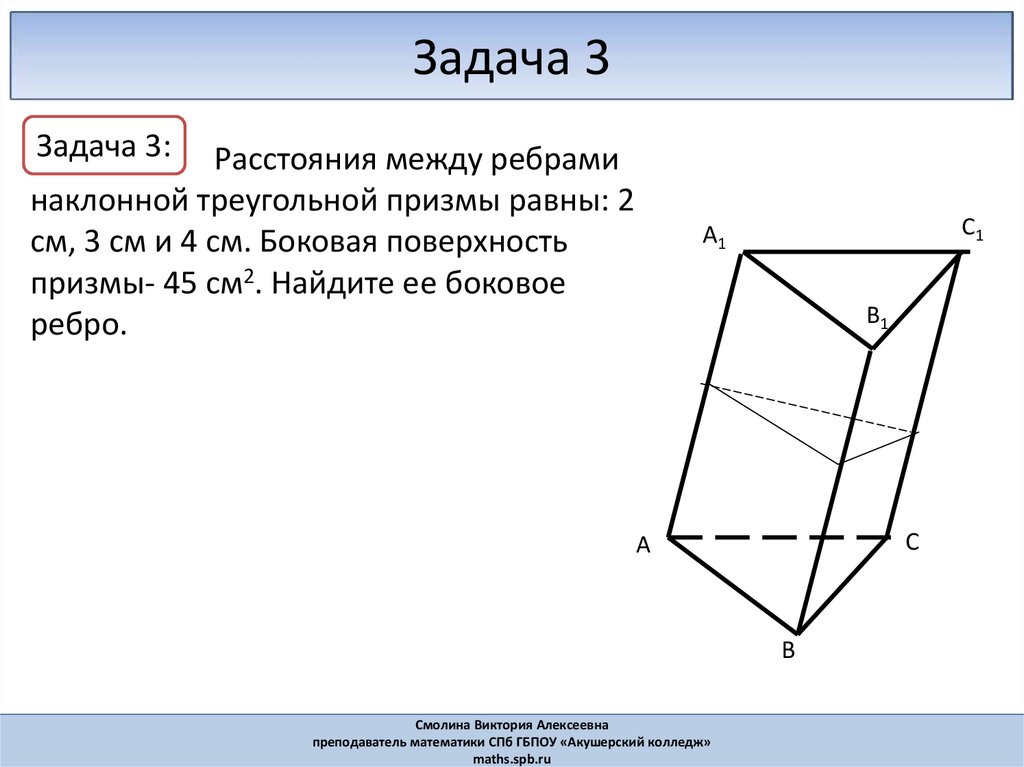
Задача 3Задача 3:
Расстояния между ребрами
наклонной треугольной призмы равны: 2
см, 3 см и 4 см. Боковая поверхность
призмы- 45 см2. Найдите ее боковое
ребро.
C1
A1
B1
C
A
B
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
25.
Задача 3ПЛАН РЕШЕНИЯ:
1. Определите чем являются боковые грани призмы.
2. Что известно про боковые ребра наклонной призмы? Как их
можно обозначить?
3. Предложите способы расчета площади боковой грани.
4. Выберите тот способ, который использует данные задачи.
5. Найдите сумму всех боковых граней. Чему равна эта сумма?
6. Решите получившееся уравнение.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
26.
Задача 4Задача 4:
Основание прямого параллелепипеда - квадрат, площадь
которого равна 16, а высота параллелепипеда в 2 раза больше
стороны основания. Найдите площадь боковой поверхности
параллелепипеда и объем.
ПЛАН РЕШЕНИЯ:
1. Найдите сторону квадрата АВСD
2. Найдите длину бокового ребра
параллелепипеда
3. Площадь боковой поверхности
параллелепипеда и объем
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
27.
Задача 5Задача 5:
Основание наклонной призмы - треугольник со
сторонами 4 см, 13 см и 15 см. Боковое ребро призмы равно
8 см и образует с плоскостью основания угол 45 . Найдите
объем призмы.
8
45
13
О
4
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
15
28.
Задача 5ПЛАН РЕШЕНИЯ:
1. Постройте высоту АО.
2. Из равнобедренного прямоугольного треугольника
найдите катет АО.
3. Найдите площадь основания по формуле Герона:
SΔ p (p a) (p b) (p c)
4. Найдите площадь основания по формуле Герона.
5. Найдите объем.
Ответ : 96 2 см2
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
29.
Задача 6Задача 6:
Объем прямоугольного параллелепипеда равен 5. Чему
будет равен объем параллелепипеда, если каждое его
ребро увеличить в три раза?
ПЛАН РЕШЕНИЯ:
1. Найдите объем параллелепипеда
АВСDA1B1C1D1
2. Увеличьте каждое ребро в 3 раза
3. Найдите объем получившегося
параллелепипеда.
4. Найдите отношение полученного
объема к объему параллелепипеда
АВСDA1B1C1D1
4. Сделайте вывод во сколько раз
изменяется объем параллелепипеда,
если его ребра увеличиваются в 3
раза.
Смолина Виктория Алексеевна
преподаватель математики СПб ГБПОУ «Акушерский колледж»
maths.spb.ru
























 mathematics
mathematics








