Similar presentations:
Уравнение прямой (различные способы задания)
1.
04.03.20242.
04.03.2024Урок № 21
Уравнение прямой
(различные способы задания)
3.
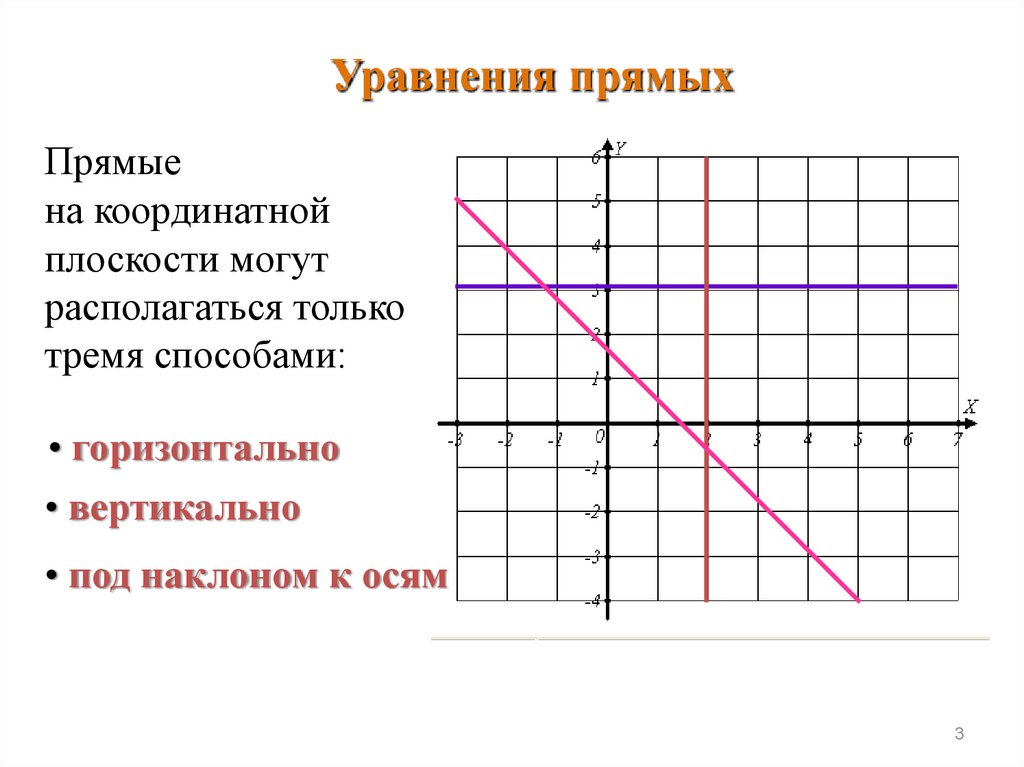
Уравнения прямыхПрямые
на координатной
плоскости могут
располагаться только
тремя способами:
• горизонтально
• вертикально
• под наклоном к осям
3
4.
Уравнение вертикальных прямыхУравнение вида x = a
на координатной плоскости задает множество
точек, имеющих одну и ту же абсциссу.
Рассмотрим, например, уравнение: x = 1
Отметим на координатной плоскости некоторые
точки, имеющие абсциссу, равную 1.
4
5.
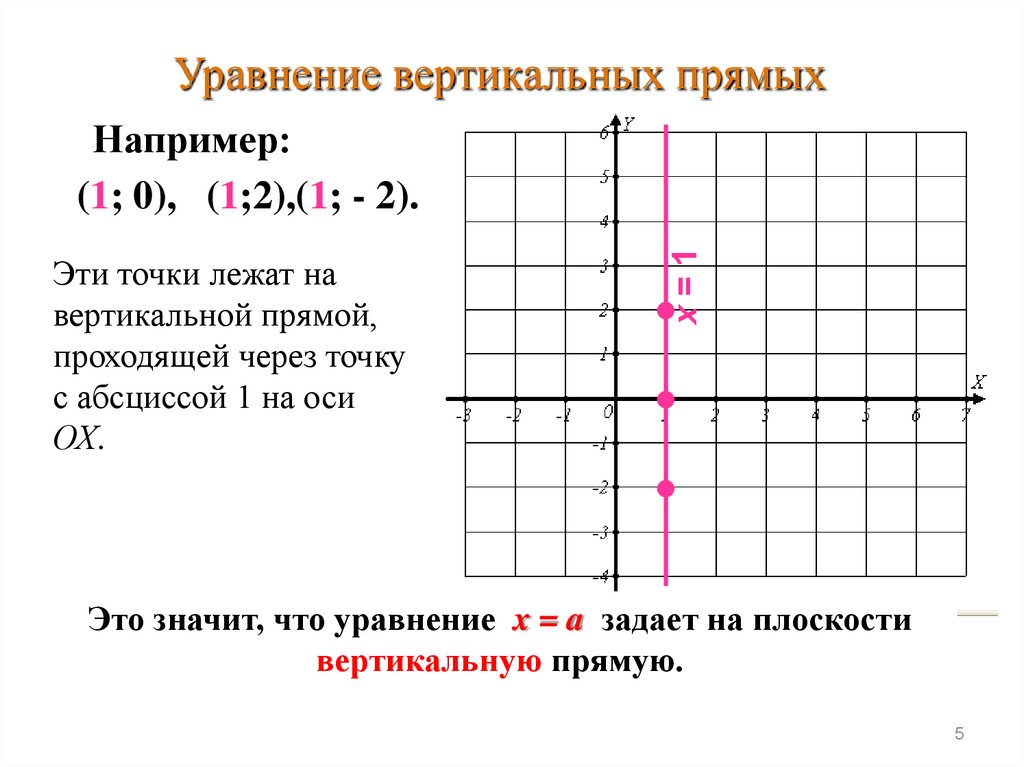
Уравнение вертикальных прямыхЭти точки лежат на
вертикальной прямой,
проходящей через точку
с абсциссой 1 на оси
ОХ.
х=1
Например:
(1; 0), (1;2),(1; - 2).
Это значит, что уравнение x = a задает на плоскости
вертикальную прямую.
5
6.
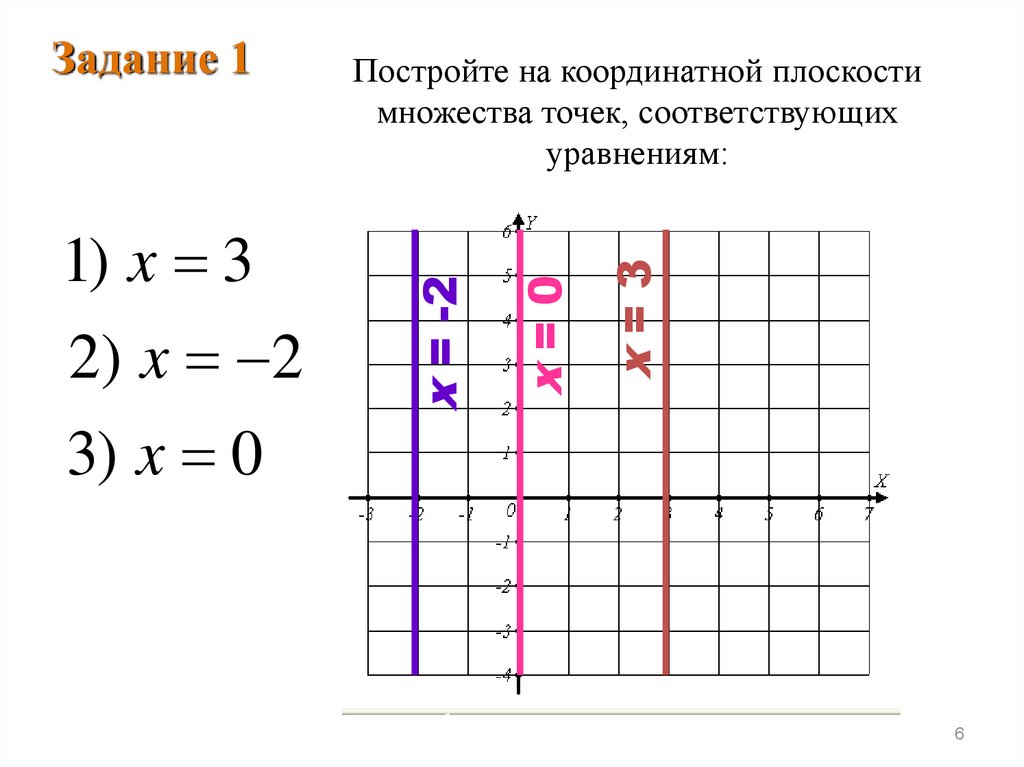
3) x 0x=3
2 ) x 2
x=0
1) x 3
Постройте на координатной плоскости
множества точек, соответствующих
уравнениям:
x = -2
Задание 1
6
7.
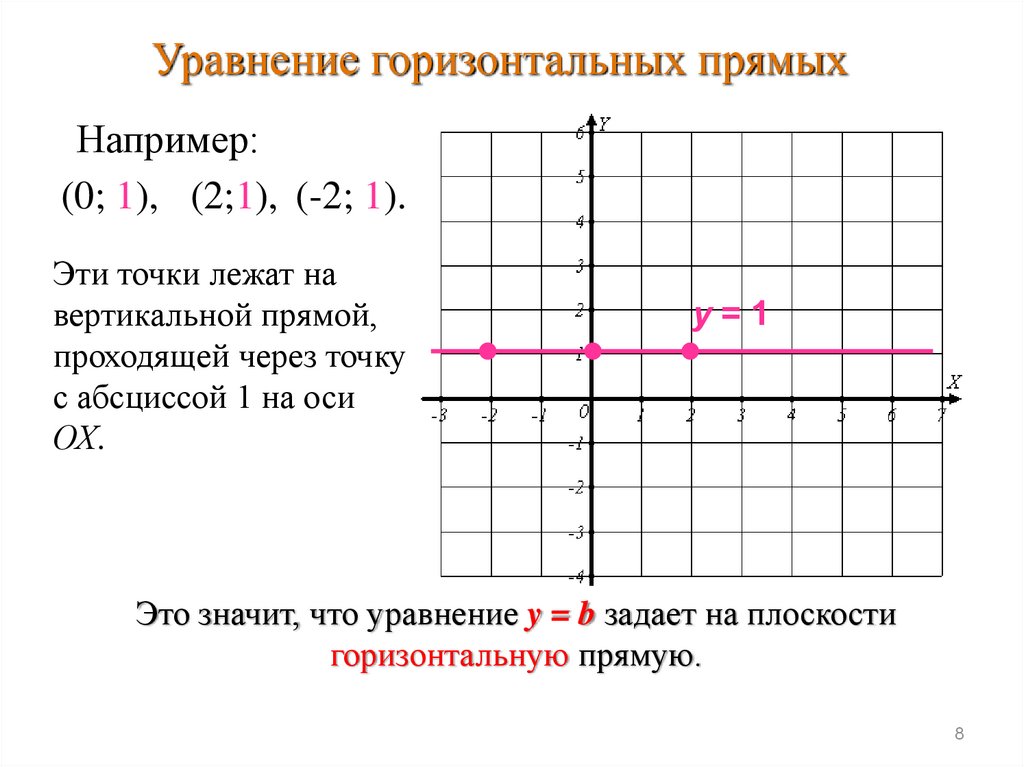
Уравнение горизонтальных прямыхУравнение вида y = b
на координатной плоскости задает множество точек,
имеющих одну и ту же ординату.
Рассмотрим, например, уравнение:
y=1
Отметим на координатной плоскости некоторые
точки, имеющие ординату, равную 1.
7
8.
Уравнение горизонтальных прямыхНапример:
(0; 1), (2;1), (-2; 1).
Эти точки лежат на
вертикальной прямой,
проходящей через точку
с абсциссой 1 на оси
ОХ.
y=1
Это значит, что уравнение y = b задает на плоскости
горизонтальную прямую.
8
9.
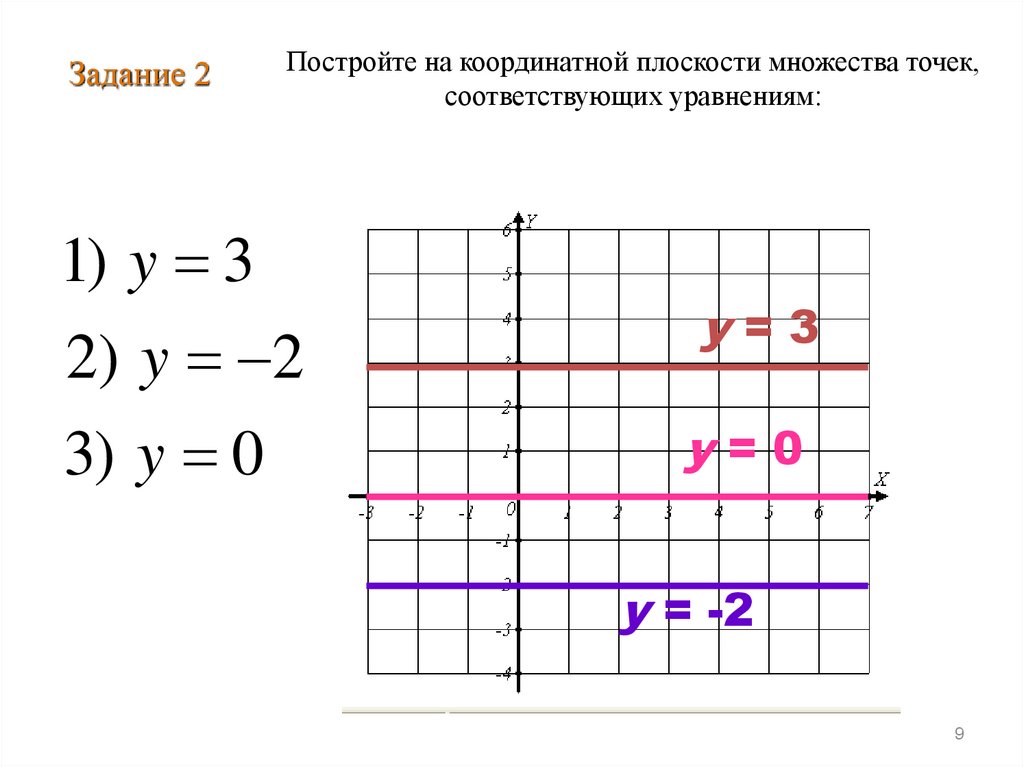
Задание 2Постройте на координатной плоскости множества точек,
соответствующих уравнениям:
1) y 3
2 ) y 2
3) y 0
y=3
y=0
y = -2
9
10. Условие перпендикулярности векторов
04.03.2024Условие перпендикулярности
векторов
Дано : а х1 ; у1 , b х 2 ; у 2
Доказать : а b , если х1 х 2 у1 у 2 0
а b
у
AOB прямоуголь ный,
А (х1;у1)
О 90
х
ОА ОВ АВ
2
2
2
АВ 2 ( х 2 х1 ) 2 ( у 2 у1 ) 2
В (х2;у2)
ОА 2 х12 у12
ОВ 2 х 22 у 22
11.
04.03.2024Дано : а х1 ; у1 , b х 2 ; у 2
Доказать : а b , если х1 х 2 у1 у 2 0
ОА ОВ АВ
2
2
2
АВ 2 ( х 2 х1 ) 2 ( у 2 у1 ) 2
ОА 2 х12 у12
ОВ 2 х 22 у 22
х12 у12 х 22 у 22 х 22 2 х1 х 2 х12 у 22 2 у1 у 2 у12
2( х1 х 2 у1 у 2 ) 0
х1 х 2 у1 у 2 0
12. Виды уравнений прямой
1.2.
3.
4.
5.
6.
7.
Уравнение прямой, проходящей через данную точку
и имеющей вектор нормали
Общее уравнение прямой
Уравнение прямой «в отрезках»
Каноническое уравнение прямой
Уравнение прямой, проходящей через две точки
Уравнение прямой, проходящей через данную точку
А(х1;у1) и имеющей угловой коэффициент к
Уравнение прямой с угловым коэффициентом к
04.03.2024
13.
04.03.2024Уравнение прямой, проходящей через данную точку и
имеющей вектор нормали n
Дано : l прямая
М ( х0 ; у0 ) l ,
l
у
n А; В К (х ;у )
M (х0 ;у0 )
х
К ( х; у ) l произвольн ая
n A; B l
n вектор нормали
MK x x0 ; y y0
n l n MK
A ( x x0 ) B ( y y0 ) 0
14.
04.03.2024Задание 3
Напишите уравнение прямой, проходящей через
точку Р(- 2;3) и перпендикулярной вектору n 4;5
15. Общее уравнение прямой
A ( x x0 ) B ( y y0 ) 0Ax Ax0 By By 0 0 Ax By ( Ax0 By 0 ) 0
Ax By C 0
Уравнение вида:
Ax By C 0
с коэффициентами А; В; С такими , что А и В не равны нулю
одновременно, называется
общим уравнением прямой.
Вектор
n A; B ортогонален этой прямой и называется
нормальным.
16. Уравнение прямой(как в учебнике).
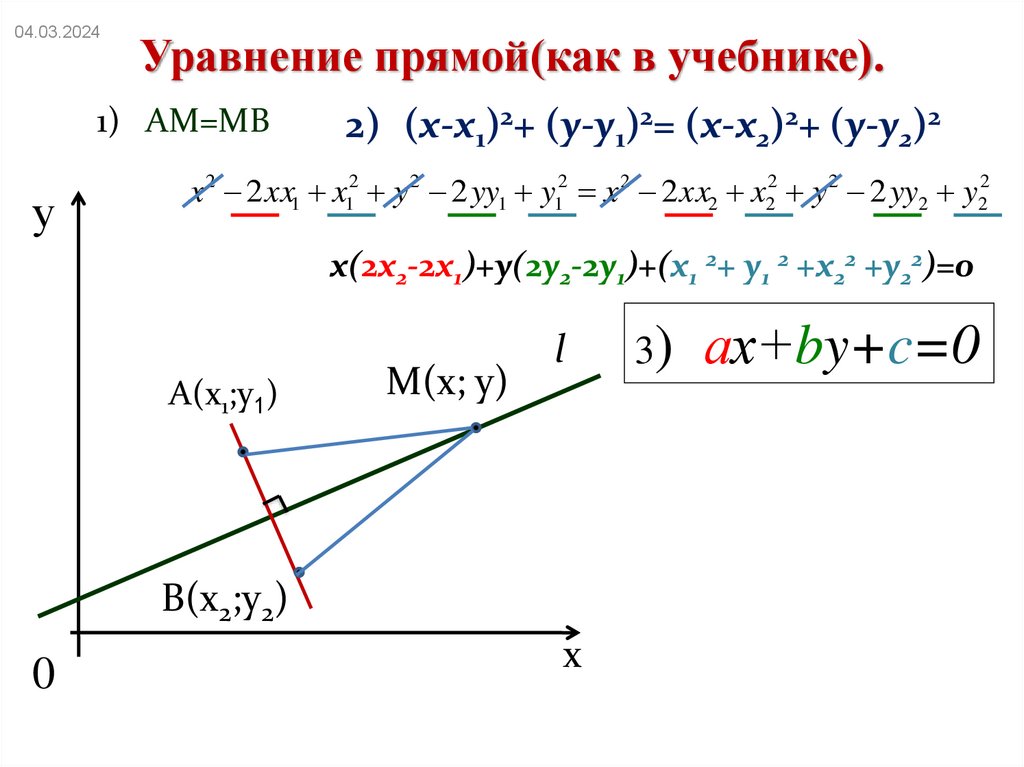
04.03.2024Уравнение прямой(как в учебнике).
1) АМ=МВ
у
2) (х-х1)2+ (у-у1)2= (х-х2)2+ (у-у2)2
x 2 2 xx1 x12 y 2 2 yy1 y12 x 2 2 xx2 x22 y 2 2 yy2 y22
х(2х2-2х1)+у(2у2-2у1)+(х1 2+ у1 2 +х22 +у22)=0
A(x1;y1)
M(x; y)
l
B(x2;y2)
0
х
3)
ах+by+c=0
17. Написать уравнение прямой, проходящей через точки А(-1; 2) и В(2; -3).
Решение:Уравнение прямой имеет вид ах+bу+с=0. тогда А и В лежат
на прямой, т. е. их координаты удовлетворяют этому
уравнению. Подставим координаты точек А и В в
уравнение:
1 1 b
b2
2
c 0,0,
a a
c
3 3
c 0.0.
c
a a2 2 b b
-3a 5b 0, b 0,6a
Подставим b 0,6a в 1 уравнение :
1а 1,2a c 0, c 0,2a.
Подставим b 0,6a и c 0,2a в уравнение ax by c 0 :
аx 0,6ay 0,2a 0, : a
x 0,6 y 0,2 0 5 5x 3 y 1 0.
04.03.2024
18. Общее уравнение прямой
Общее уравнение прямой называется полным, если всекоэффициенты А, В, и С отличны от нуля.
В противном случае уравнение называется неполным.
Виды неполных уравнений:
1) C 0;
Ax By 0
2) B 0;
Ax C 0
3) A 0;
By C 0
4) B C 0;
Ax 0 x 0
A C 0;
By 0 y 0
5)
y
0
х
19. Уравнение прямой в отрезках
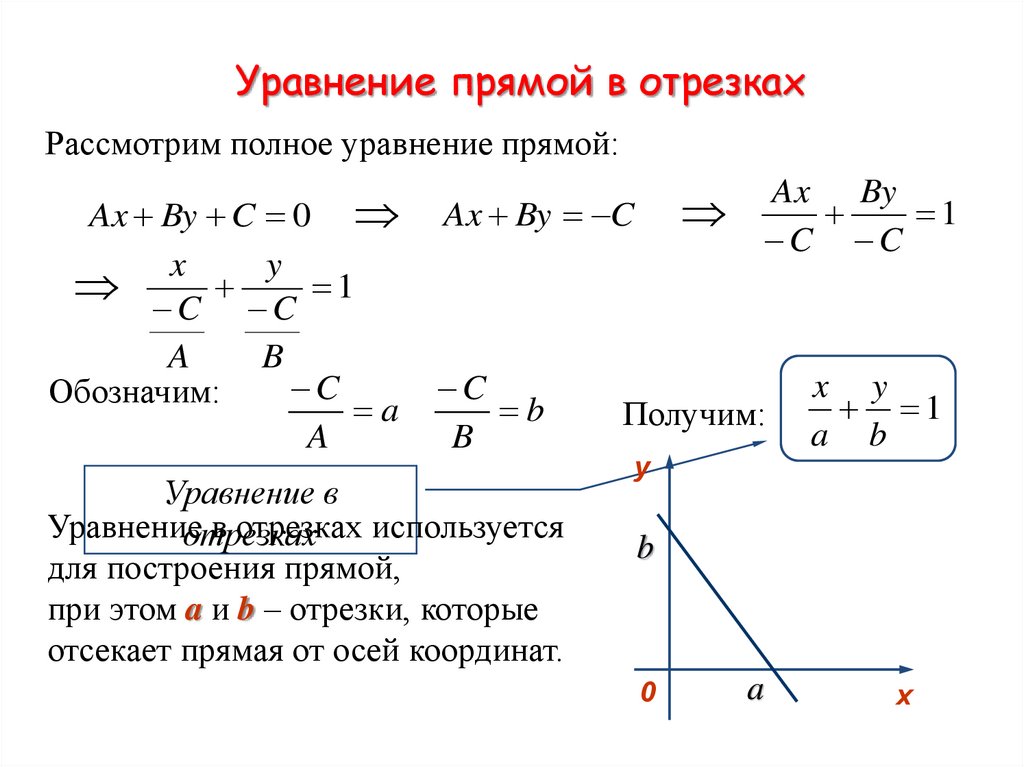
Рассмотрим полное уравнение прямой:Ax By C 0
x
y
C C 1
A
B
C
Обозначим:
a
A
Ax By C
C
b
B
Уравнение в
Уравнение
в отрезках используется
отрезках
для построения прямой,
при этом a и b – отрезки, которые
отсекает прямая от осей координат.
Ax By
1
C C
Получим:
x y
1
a b
y
b
0
a
х
20.
04.03.2024Задание 4
Прямая задана уравнением 3х – 5у + 15 = 0.
Напишите уравнение этой прямой «в отрезках».
Сделайте чертеж
21. Каноническое уравнение прямой
Любой ненулевой вектор, параллельный данной прямой,называется направляющим вектором этой прямой.
Требуется найти уравнение прямой, проходящей через
заданную точку М0(х0; у0 ) и параллельно заданному вектору
Очевидно, что точка М (х; у )
лежит на прямой, только в том
случае, если векторы
q l; m
и
q
M 0 M x x0 ; y y0
q l; m
М (х; у )
М0(х0; у0 )
коллинеарны.
По условию коллинеарности получаем:
x x0
y y0
l
m
Каноническое уравнение
прямой
22.
04.03.2024Задание 5
Напишите уравнение прямой , проходящей через
точку Р(- 2; - 5) в направлении вектора а 2;3
23. Уравнение прямой, проходящей через две точки
Пусть прямая проходит через две заданные и отличные другот друга точки: М1(х1; у1 ) и М2(х2; у2 ).
q
М2(х2; у2 )
М1(х1; у1 )
Тогда в качестве направляющего вектора в каноническом
уравнении можно взять вектор:
q M 1M 2 x2 x1 ; y2 y1
x x1
y y1
y2m y1
x2 l x1
Уравнение прямой,
проходящей через две
заданные точки
24.
04.03.2024Задание 6
Напишите уравнение прямой , проходящей через
точки А(- 2; - 3) и В(- 5; 4)
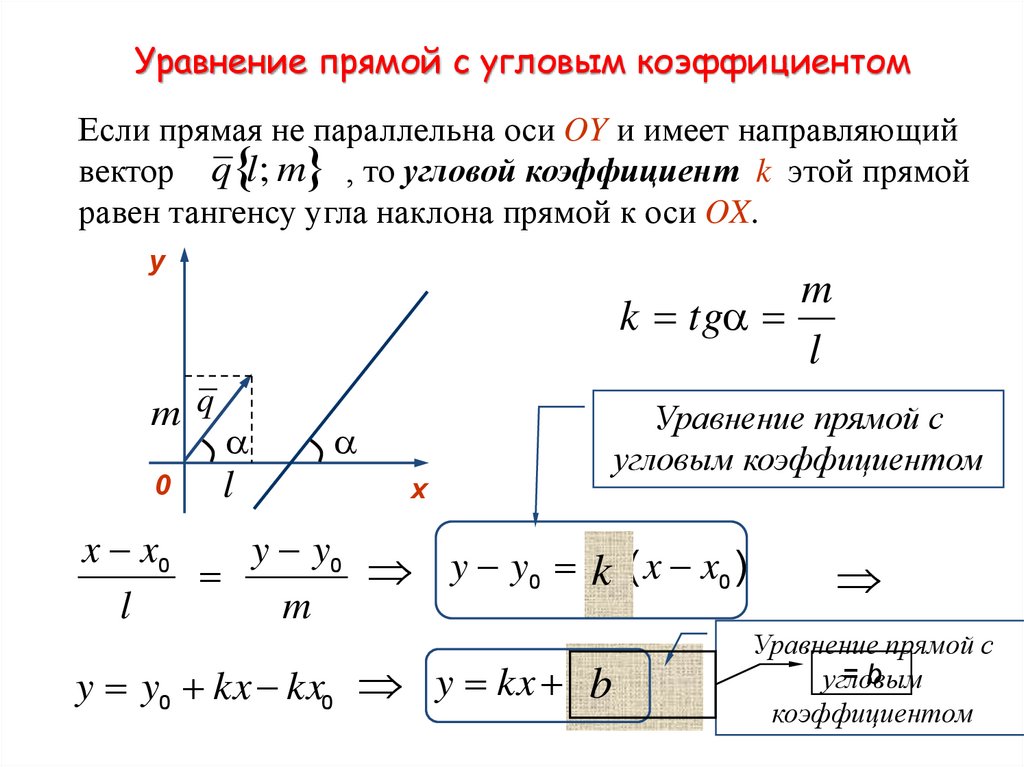
25. Уравнение прямой с угловым коэффициентом
Если прямая не параллельна оси OY и имеет направляющийвектор q l; m , то угловой коэффициент k этой прямой
равен тангенсу угла наклона прямой к оси OX.
y
mq
0
m
k tg
l
l
х
Уравнение прямой с
угловым коэффициентом
m
x x0
y y0
y y0 k ( x x0 )
l
l
m
y y0 kx kx0 y kx yb0 kx0
Уравнение прямой с
=b
угловым
коэффициентом
26.
04.03.2024Задание 7
Прямая задана уравнением 3х – 4у + 8 =0.
Определите угловой коэффициент. Постройте
прямую
27.
04.03.2024Задание 8
Прямая задана уравнением 13х – 5у – 65 =0
Напишите уравнение прямой
1) С угловым коэффициентом
2) «в отрезках»
3) каноническое
28. Пример
Прямая проходит через точку М(1; 2 ) и имеетнаправляющий вектор: q{ 1; 3}
Написать: каноническое, общее уравнение прямой, уравнение прямой в
отрезках, уравнение с угловым коэффициентом.
Найти нормальный вектор прямой, отрезки, которые отсекает прямая от осей
координат и угол, который составляет прямая с осью OX.
1. Каноническое уравнение:
2. Общее уравнение:
3x y 5 0
x 1 y 2
1
3
x 1 y 2
1
3
N {3;1}
3 ( x 1) ( y 2)
29.
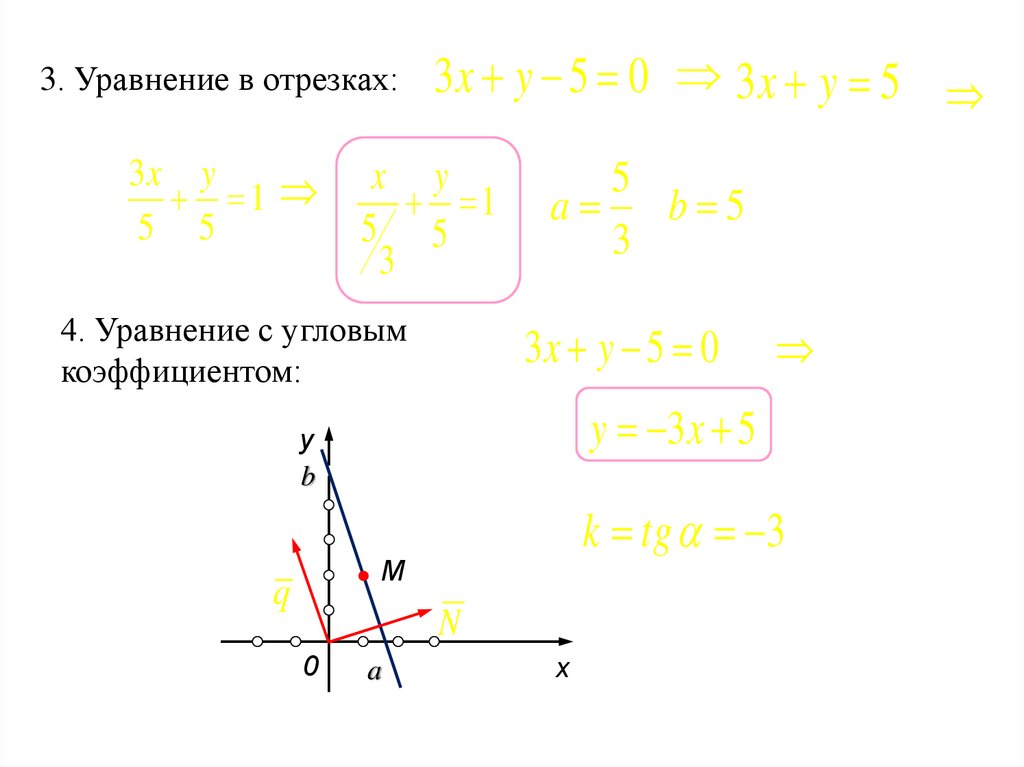
3. Уравнение в отрезках:3x y
1
5 5
3x y 5 0 3x y 5
x y
1
5 5
3
4. Уравнение с угловым
коэффициентом:
5
a
b 5
3
3x y 5 0
y 3 x 5
y
b
k tg 3
М
q
N
0
a
х
30.
31.
04.03.202432.
04.03.202433.
04.03.202434.
Домашнее задание35.
04.03.2024Урок № 22
Взаимное расположение
двух прямых
36.
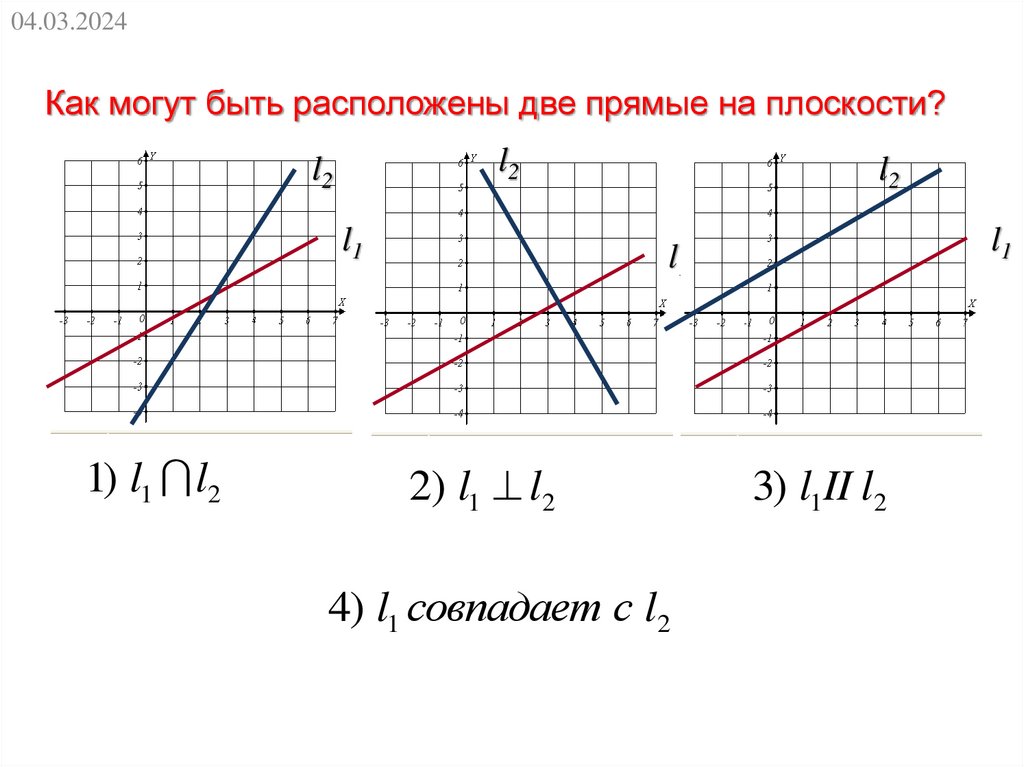
04.03.2024Как могут быть расположены две прямые на плоскости?
l2
l2
l1
1) l1 l2
l2
l1
l1
2) l1 l2
4) l1 совпадает с l2
3) l1II l2
37.
04.03.2024Пусть даны две прямые
l1 : A1 x B1 y C1 0
l2 : A2 x B 2 y C2 0
1) Прямые пересекаются, значит векторы нормали
n1 A1; B1 II n2 A2 ; B2
Не коллинеарны
A1 B1
A1 A2
k1 k 2
A2 B2
B1 B2
38.
04.03.2024Пусть даны две прямые
l1 : A1 x B1 y C1 0
l2 : A2 x B 2 y C2 0
2) Прямые перпендикулярны
n1 A1; B1 n2 A2 ; B2
A1 A2 B1 B2 0
A1 A2
1 0
B1 B2
A1 A2
1 k1 k 2 1
B1 B2
39.
04.03.2024Пусть даны две прямые
l1 : A1 x B1 y C1 0
l2 : A2 x B 2 y C2 0
3) Прямые параллельны, значит векторы нормали
n1 A1; B1 II n2 A2 ; B2
коллинеарны, но не лежат
на одной прямой
A1 B1
A1 A2
A2 B2
B1 B2
A1 A2 С1
но
k1 k 2 , b1 b2
B1 B2 С2
40.
04.03.2024Пусть даны две прямые
l1 : A1 x B1 y C1 0
l2 : A2 x B 2 y C2 0
4) Прямые совпадают, значит векторы нормали
n1 A1; B1 II n2 A2 ; B2
коллинеарны, и лежат на
одной прямой
A1 B1
A1 A2
A2 B2
B1 B2
A1 A2 С1
k1 k 2 , b1 b2
B1 B2 С2
41.
04.03.2024Определите взаимное расположение прямых
1) 3х + 4у - 1 = 0 и 2х + 3у – 1 = 0
2) 2х + 2у +1 = 0 и 4х + 4у + 3 = 0
3) х + у + 1 = 0 и 2х + 2у + 2 = 0
№ 976
42.
04.03.2024№ 1005
43.
04.03.2024Написать уравнение прямой, проходящей через точку
4
пересечения прямых х + 6у + 5 =0 и 3х – 2у + 1 =0 и точку А ;1
5
44.
04.03.2024Написать уравнение прямой, проходящей через точку А (-2;-5),
параллельно прямой 3х + 4у + 2 =0
45.
04.03.2024Найти проекцию точки М (-6;4) на прямую, заданную уравнением
4х – 5у + 3 =0
46. Расстояние от точки до прямой
Дано :у
l : Ax By C 0
M (х0 ;у0 )
М1 (х1;у1)
0
04.03.2024
M ( x0 ; y 0 ) l
Найти : d (от M до l )
d M1M
n A; B
n A; B вектор нормали
х
n l
n II M 1 M
l
M 1M l
47.
04.03.2024х0 х1 у0 у1
к
А
В
х0 х1 А к
у 0 у1 В к
или х1 х0 А к
у1 у 0 В к
т.к. М 1 l , то Ах1 Ву 1 С 0
А( х0 к А) В( у 0 к В) С 0
Ах0 к А Ву 0 к В С 0
2
2
к ( А В ) Ах0 Ву 0 С
2
2
Ах0 Ву 0 С
к
2
2
А В
48.
04.03.2024d M 1 M ( x0 x1 ) 2 ( y 0 y1 ) 2
d ( A k ) (B k ) k A B
2
2
2
Ax0 By 0 C
2
2
d
A B
2
2
A B
d
Ax0 By 0 C
A B
2
2
2
49. Следствия
• Если М0 = О(0;0) то dC
A B
2
2
• Если у = кх + b, то
кх у b 0
A k , B 1, C b d
04.03.2024
kx0 y 0 b
k 1
2
50.
04.03.2024Даны уравнения сторон треугольника
АВ: х + 3у – 7 =0
ВС: 4х – у – 2 = 0
АС: 6х + 8у – 3,5 = 0
Найти длину высоты, опущенной из вершины В на сторону АС
51.
04.03.2024Найти расстояние от точки А(- 2; 3) до прямой у = 0,75х + 0,5
52.
04.03.2024Найти расстояние между прямыми
3х + 4у - 24 =0 и 3х – 4у + 6 = 0
53. Домашняя контрольная работа
04.03.2024Домашняя контрольная работа
1.
2.
3.
4.
5.
6.
7.
8.
Дано: А(8;-1), В(-8;11), С(-1;-13)
Найти:
Длины сторон АВ и ВС треугольника АВС
Уравнения сторон АВ и ВС
Уравнение медианы, проведенной из вершины А
Уравнение высоты, проведенной из вершины А
Длину высоты, проведенной из вершины А
Уравнение биссектрисы внутреннего угла
В.(используйте формулу для вычисления координат
точки, делящей отрезок в данном отношении)
Площадь треугольника АВС.
Сделать чертеж (в натуральную величину)





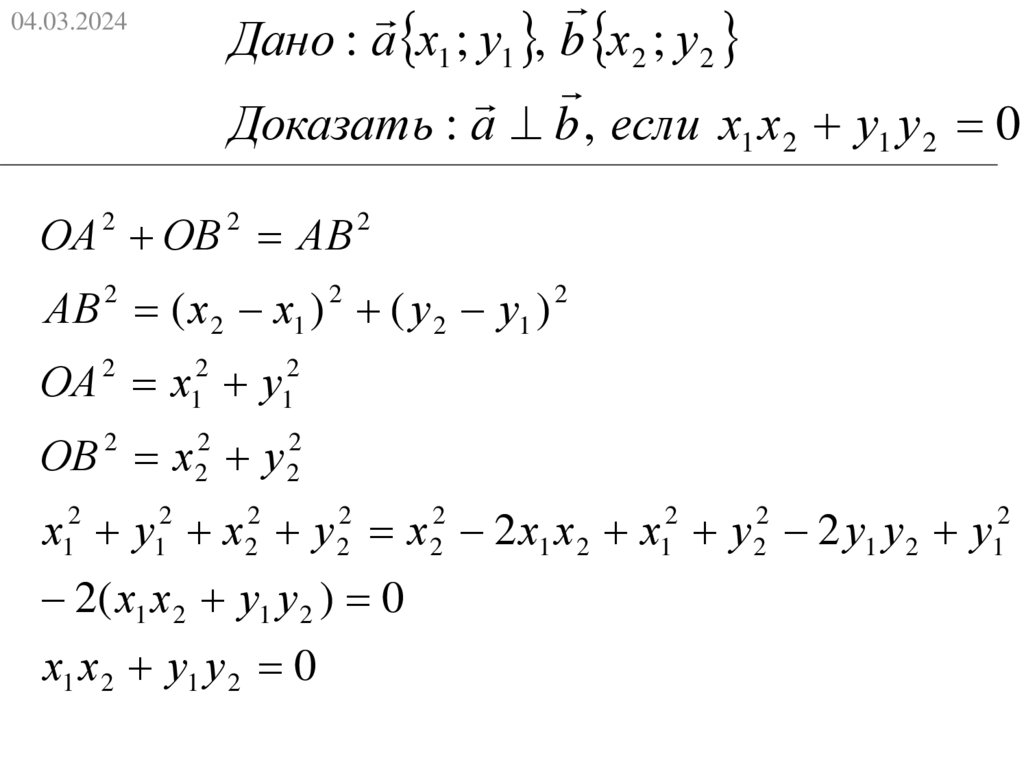




























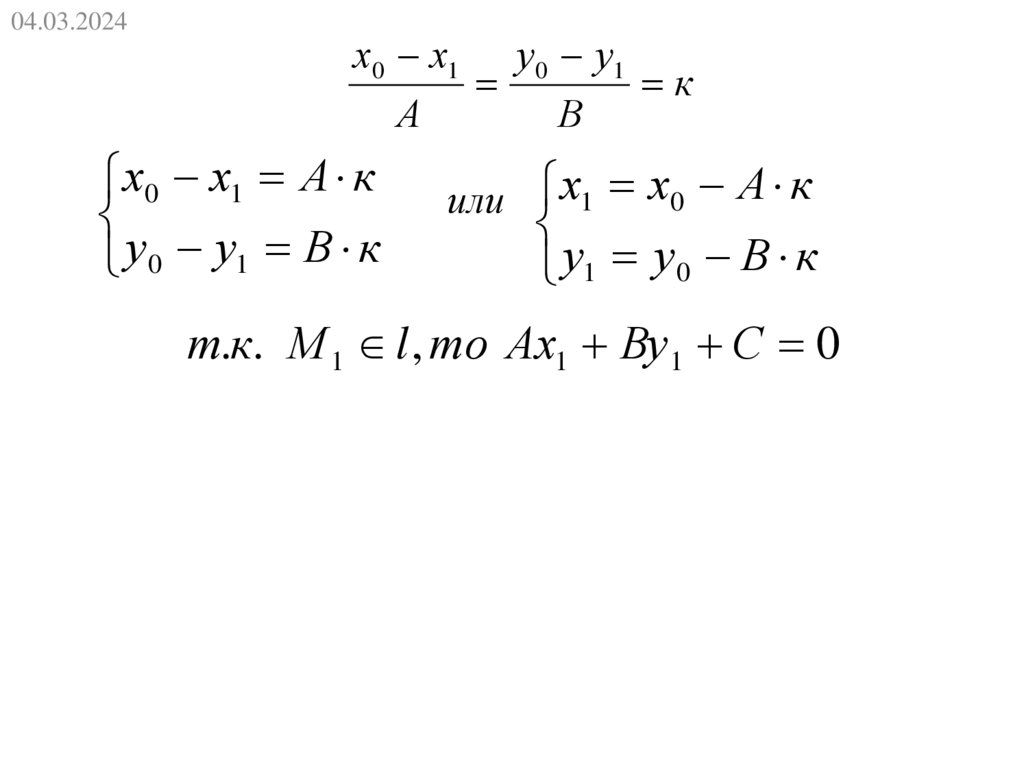
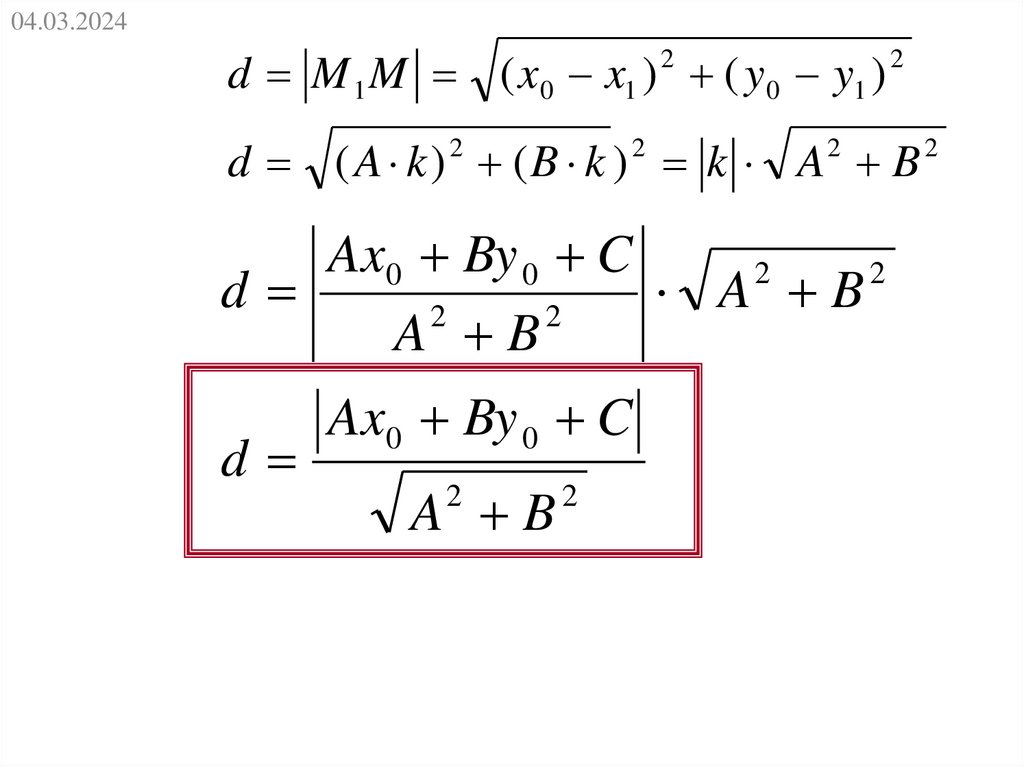





 mathematics
mathematics








