Различные виды уравнения прямой на плоскости

1. Различные виды уравнения прямой на плоскости

y=kx+b
y y1
y 2 y1
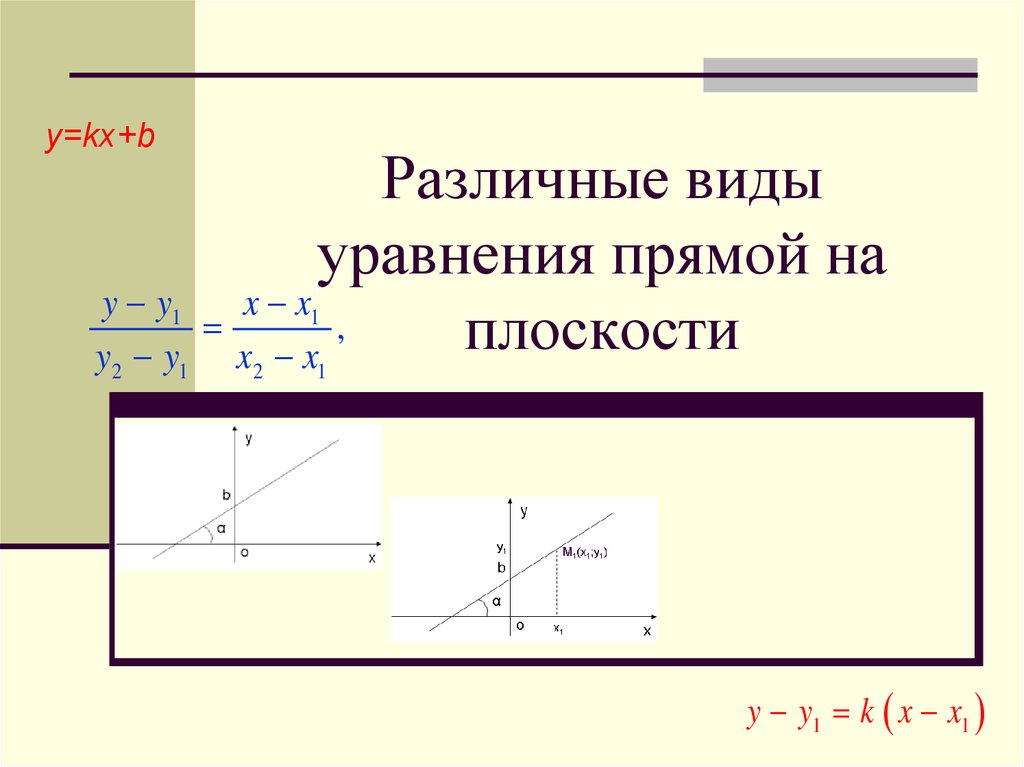
Различные виды
уравнения прямой на
x x
,
плоскости
x x
1
2
1
y y1 k x x1

2. 1.Уравнение прямой с угловым коэффициентом:

y=kx+b
y
k- угловой
коэффициент
прямой
b
α
o
x
k tg
α - угол наклона прямой к оси Ох, где
0
2
b - ордината точки пересечения прямой
с осью Оу

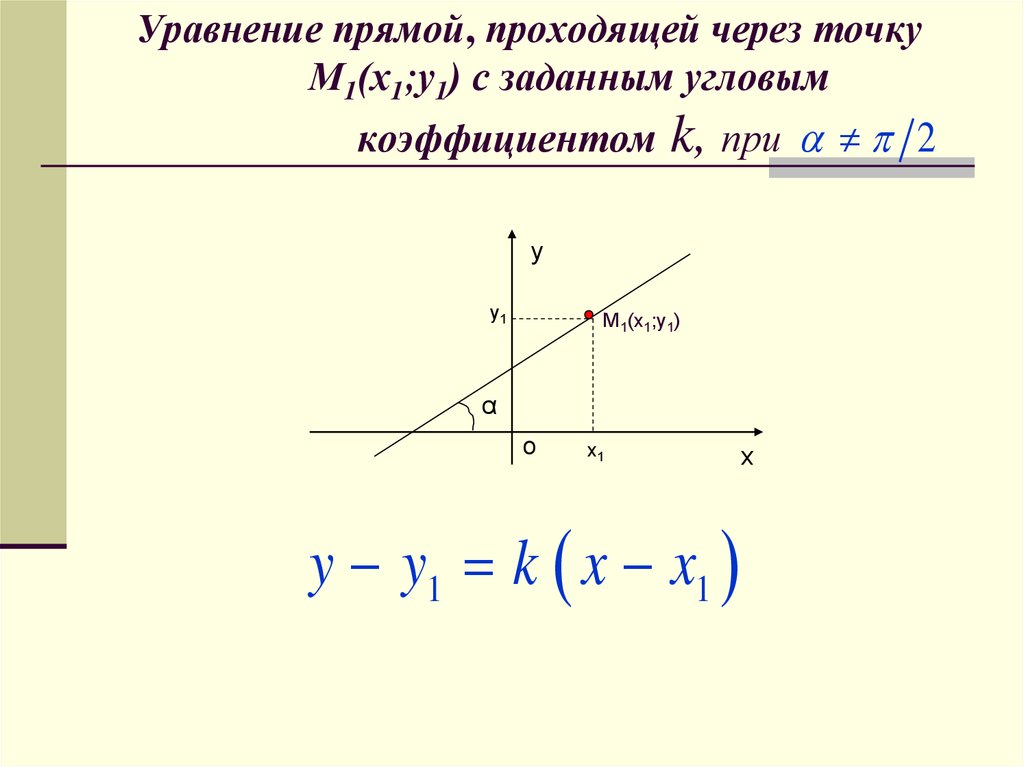
3. Уравнение прямой, проходящей через точку М1(х1;у1) с заданным угловым коэффициентом k, при

y
у1
М1(х1;у1)
α
o
x1
y y1 k x x1
x
2

4. Уравнение прямой, проходящей через точку М1(х1;у1), но не имеющей углового коэффициента, при

2
y
Х=Х1
у1
М1
o
x1
x

5. Уравнение прямой, проходящей через две заданные точки М1(х1;у1) и М2(х2;у2)

y y1
x x1
,
y 2 y1 x2 x1
если
x1 x 2 и y 1 y 2
y
y2
М2
у1
М1
o
x1
x2
x
y
x x 1 , если x 1 x 2 , но y 1 y 2
y2
М2
у1
М1
o
x1
x

6. Уравнение прямой, проходящей через две заданные точки М1(х1;у1) и М2(х2;у2)

y
М1
y1
y y 1 , если x 1 x 2 , но y 1 y 2
o
x1
М2
x2

7. Общее уравнение прямой на плоскости:

Ax+By+C=0, где А,В,С – числа
A2 B 2 0
Если А=0 В=0 уравнение прямой принимает вид: у=у1 ,
прямая параллельна оси Ох, угловой коэффициент равен 0;
Если А=0 В=0 уравнение прямой принимает вид: х=х1,
прямая параллельна оси Oy, углового коэффициента не
имеет;
Если А=0 В=0, то уравнение прямой принимает вид:
y=kx+b, где: k=A / B

8. 1. Угловой коэффициент прямой, проходящей через две точки М1(х1;у1) и М2(х2;у2)

П
Р
И
Л
О
Ж
Е
Н
И
Я
1. Угловой коэффициент прямой, проходящей
через две точки М1(х1;у1) и М2(х2;у2)
y 2 y1
k
, x1 x 2
x2 x1

9. 2. Острый угол φ между прямыми, заданными уравнениями

П
Р
И
Л
О
Ж
Е
Н
И
Я
2. Острый угол φ между прямыми,
заданными уравнениями
y=k1x+b1
и
y=k2x+b2
вычисляется по формуле:
k 2 k1
tg
1 k1 k 2

10. 3. Точка пересечения прямых, заданных общими уравнениями

П
Р
И
Л
О
Ж
Е
Н
И
Я
3. Точка пересечения прямых,
заданных общими уравнениями
A1x+B1y+C1=0 и A2x+B2y+C2=0,
находится как решение системы:
A1 x B1 y C1 0
A2 x B2 y C 2 0.

11. 4. Координаты x0 ,y0 середины отрезка M1 , M2 между точками М1(х1;у1) и М2(х2;у2)

П
Р
И
Л
О
Ж
Е
Н
И
Я
4. Координаты x0 ,y0 середины отрезка M1 , M2
между точками М1(х1;у1) и М2(х2;у2)
x2 x1
x0
,
2
y 2 y1
y0
.
2

12. 5. Расстояние |M1M2| между точками М1(х1;у1) и М2(х2;у2)

П
Р
И
Л
О
Ж
Е
Н
И
Я
5. Расстояние |M1M2| между точками
М1(х1;у1) и М2(х2;у2)
М 1М 2
x2 x1 y 2 y1
2
2

13. 6. Необходимое и достаточное условие параллельности двух прямых

П
Р
И
Л
О
Ж
Е
Н
И
Я
6. Необходимое и достаточное
условие параллельности двух прямых
Необходимое и достаточное условие
параллельности двух прямых, имеющих
угловые коэффициенты k1 и k2 :
k1=k2

14. 7. Необходимое и достаточное условие перпендикулярности двух прямых

П
Р
И
Л
О
Ж
Е
Н
И
Я
7. Необходимое и достаточное условие
перпендикулярности двух прямых
Необходимое и достаточное условие
перпендикулярности двух прямых, имеющих
угловые коэффициенты k1 и k2 :
1
k2 .
k1

15. Примеры:

П р и м е р 1. Дано общее уравнение прямой:
2 x 3 y 12 0
Найти угловой коэффициент прямой.
Р е ш е н и е. Решим уравнение относительно у получим
уравнение прямой с угловым коэффициентом:
3 y 2 x 12
Отсюда заключаем:
О т в е т: 2/3
2
y x 4
3
k = 2/3 - угловой коэффициент прямой.

16. Примеры:

П р и м е р 2. Составить уравнение прямой, проходящей
через точку А(-1;3) и составляющей с осью Ох угол 135о.
Р е ш е н и е. Так как в данном случае
k=tg135o=-1 и
x1=-1, y1=3, то уравнение прямой будет иметь вид:
y-3=-1(x+1)
Отсюда получаем: у = -х+2 – искомое уравнение
прямой.
О т в е т: у = -х+2

17. Примеры:

П р и м е р 3. Составить уравнение прямой, проходящей через точку
пересечения прямых:
x
y
1
0
параллельно прямой:
2x 3y 4 0
3x y 7 0
Р е ш е н и е. а) Найдем точку пересечения двух прямых, для этого,
решим систему уравнений:
x y 1 0
2 x 3 y 4 0,
x 7
у 6
Следовательно, искомая точка пересечения –
М1(7;-6)
б) Составим уравнение прямой, проходящей через данную точку
параллельно прямой:
3x y 7 0
М1(7;-6)

18. Примеры:

Найдем угловой коэффициент
k1 прямой:
y 3x 7 k1 3
3x y 7 0
Из условия параллельности двух прямых находим угловой
k1= k2=3
y y1 k x x1
коэффициент искомой прямой:
Пользуясь формулой:
, находим уравнение
прямой, проходящей через точку М1(7;-6) с угловым
коэффициентом
k2=3:
y 6 3 x 7 3 x y 27 0.
О т в е т:
3 x y 27 0.

19. Нормальный вектор прямой

n
l
a
Если вектор n
перпендикулярен
направляющему вектору a
прямой l , то он
называется нормальным
вектором прямой l .
Прямая задана общим
уравнением
Ax By C 0,
Тогда вектор n A, B
является нормальным вектором
этой прямой.

20. Нормальный вектор прямой

З
А
Нормальный вектор прямой
Д Найти уравнение
А
Ч
А
прямой l , которая проходит
через точку M 0 ( x0 , y0 )
и имеет нормальный вектор
n A, B .
Решение. Векторы MM 0 ( x x0 , y y0 ), n
перпендикулярны, их скалярное произведение равно
нулю: n M 0 M 0. A( x x0 ) B ( y y0 ) 0.
Это и есть искомое уравнение.

21. Расстояние от точки до прямой

Теорема. Расстояние
от точки M ( x , y )
0
0
0
до прямой, заданной
общим уравнением
Ax By C 0,
вычисляется формулой
d
Ax0 By0 C
A2 B 2
.

22. Расстояние от точки до прямой

З
А
Расстояние от точки до прямой
M 0 (1,5) до прямой,
Найти расстояние от точки
Д
заданной общим уравнением
3x 4 y 3 0
А Решение.
d
Ч
d
А
Ответ:
4.
Ax0 By0 C
A B
2
2
3 1 4 5 3
3 4
2
2
.
4.

23. Кривые второго порядка

О
К
Р
У
Ж
Н
О
С
Т
Ь
Кривые второго порядка
ОКРУЖНОСТЬ
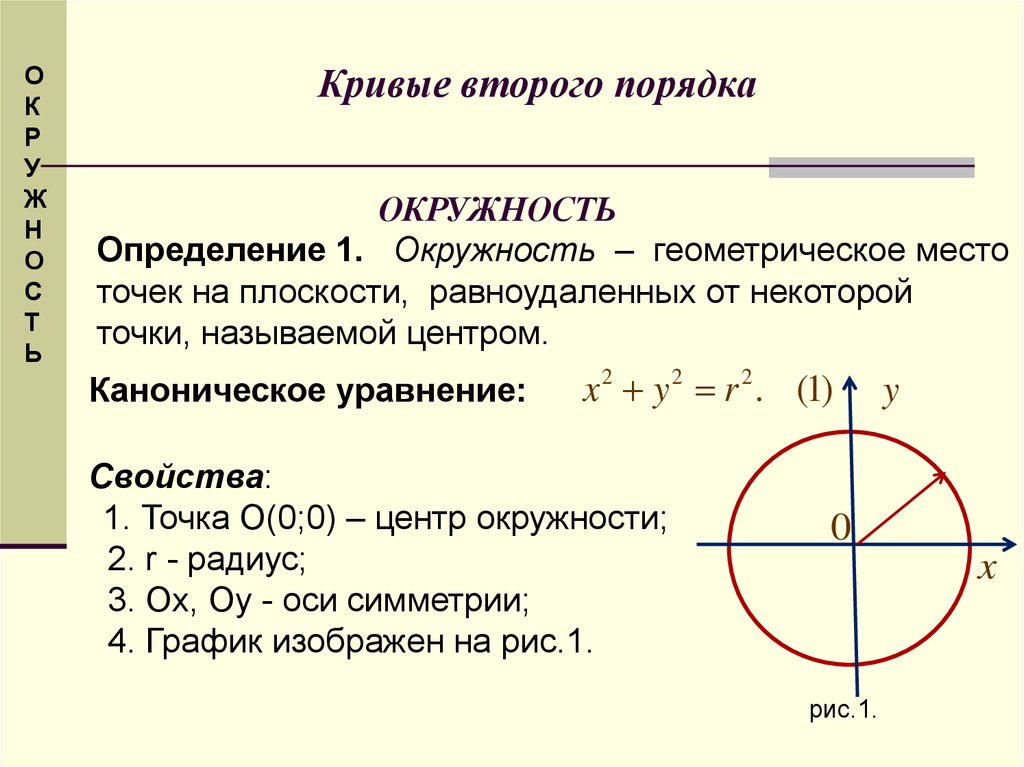
Определение 1. Окружность – геометрическое место
точек на плоскости, равноудаленных от некоторой
точки, называемой центром.
Каноническое уравнение:
x 2 y 2 r 2 . (1)
Свойства:
1. Точка О(0;0) – центр окружности;
2. r - радиус;
3. Ox, Oy - оси симметрии;
4. График изображен на рис.1.
y
0
x
рис.1.

24. Кривые второго порядка

О
К
Р
У
Ж
Н
О
С
Т
Ь
Кривые второго порядка
Окружность, задаваемая уравнением
x x0 y y0
2
2
r 2 . (2)
обладает свойствами:
1.Точка O1 ( x1 , y1 ) центр окружности;
2. r радиус;
3. Прямые x x0 , y y0
оси симметрии;
4. График окружности (2) изображен
на рис.2 и получается из окружности с
уравнением (1) параллельным переносом
на вектор OO1 .
y
y0
0
рис.2.
01
x0

25. Кривые второго порядка

Э
л
л
и
п
с
Кривые второго порядка
Определение. Эллипс –
геометрическое место точек на
плоскости, для каждой из которых сумма расстояний до двух
данных точек, называемых фокусами, есть величина постоянная.
Эллипс –
геометрическое место точек на плоскости,
координаты которых в некоторой прямоугольной системе
координат Oxy удовлетворяет уравнению
x2 y 2
2 1
2
a
b
a b
(1)
При a b уравнение (1) является уравнением окружности
радиуса a с центром в начале координат.

26. Кривые второго порядка

Свойства:
Э
л
л
и
п
с
1. Центр эллипса точка О(0;0);
А1 a;0 , A2 a;0 , B1 0; b , B2 0; b
2. Вершины эллипса точки
3. A1 A2 2a, B1B2 2b оси эллипса;
4. a, b - полуоси эллипса;
5. Оси симметрии Оx, Oy;
F1 c;0 , F2 c;0 ,
6. Фокусы эллипса – точки,
F1 0; c , F2 0; c ,
где
если a b;
c b2 a2 ,
a b
у
где
b a
у
В1
В1
F1
А2
А2
А1
F2
F1
O
В2
x
А1
O
x
F2
В2
c a2 b2 ,
если a b;

27. Кривые второго порядка

Э
л
л
и
п
с
Эллипс, задаваемый уравнением x x0 2
обладает свойствами:
Центр эллипса точка
a
2
2
y y0
О1 x0 ; y 0 ;
2. Вершины эллипса точки
А1 х0 a; у0 , A2 х0 a; у0 , B1 х0 ; у0 b , B2 х0 ; у0 b ;
3.
A1 A2 2a, B1 B2 2b оси эллипса;
4. a, b полуоси эллипса;
5. Оси симметрии прямые
x x0 , y y 0 ;
6. Фокусы эллипса – точки
F1 х0 c; у0 , F2 х0 c; у0 , где c a 2 b 2 , если a b;
F1 х0 ; у0 c , F2 х0 ; у0 c , где c b 2 a 2 , если b a;
b
2
1, a b

28. Кривые второго порядка

Г
И
П
Е
Р
Б
О
Л
А
Определение. Гипербола – геометрическое место точек
на плоскости, для каждой из которых модуль разности
расстояний до двух данных точек, называемых
фокусами, есть величина постоянная.
Каноническое уравнение:
x2 y2
2 1
2
a
b
(а)
или
y2 x2
1.
b2 a2
(б)

29. Кривые второго порядка

Свойства:
1.
Вершины:
А1 a;0 , A2 a;0 – для гиперболы (а);
B1 0; b , B2 0; b – для гиперболы (б);
2. Полуоси:
а
b
действительная
мнимая
для гиперболы (а);
а
b
мнимая
действительная
для гиперболы (б);
3. Фокусы гиперболы: точки
F 0;
b , F 0;
для гиперболы (б);
F1 a 2 b 2 ;0 , F2 a 2 b 2 ;0 для гиперболы (а),
1
a2
2
2
a2 b2

30. Кривые второго порядка

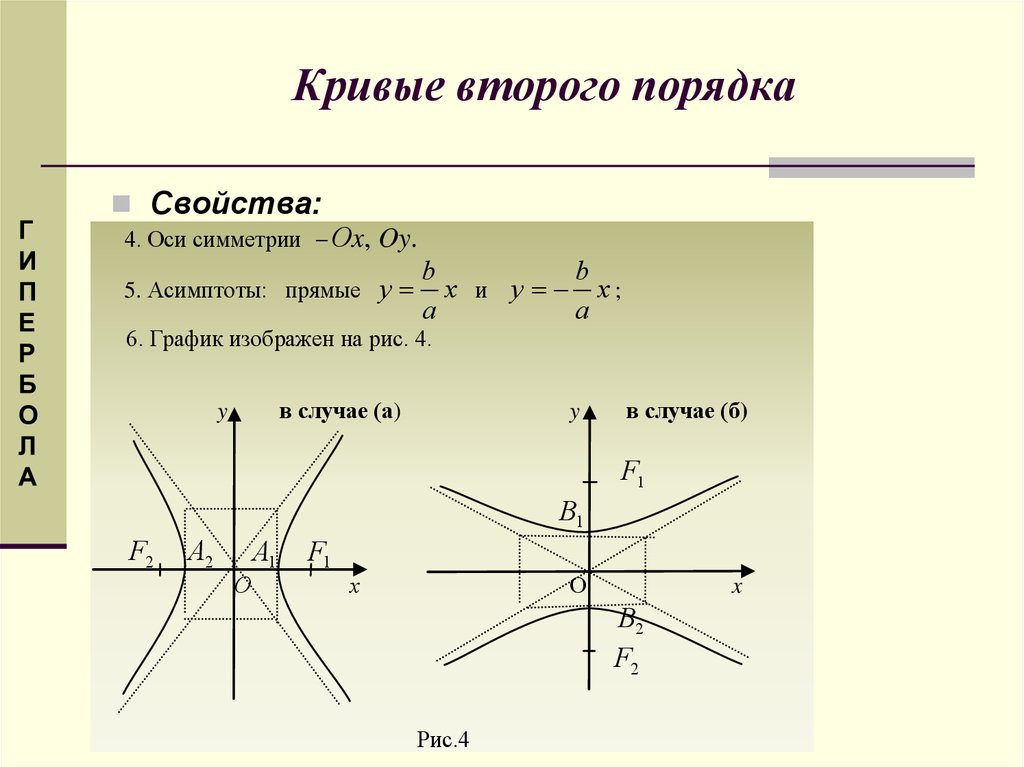
Свойства:
4. Оси симметрии Оx,
Oy.
5. Асимптоты: прямые y
b
b
x и y x;
a
a
6. График изображен на рис. 4.
в случае (а)
y
y
в случае (б)
F1
В1
F2
А2
А1
О
F1
x
О
x
В2
F2
Рис.4

31. Кривые второго порядка

Гиперболы, задаваемые уравнениями:
x x 0 2 y y 0 2
a
2
b
2
y y0 2 x x0 2
1
b
2
a
2
1
А1 х0 a; у0 , A2 х0 a; у0 – для гиперболы (а);
Вершины:
B1 х0 ; у0 b , B2 х0 ; у0 b – для гиперболы (б);
2. Полуоси:
3.
а
b
действительная
мнимая
для гиперболы (а);
а
b
мнимая
действительная
для гиперболы (б);
Фокусы гиперболы: точки
F х ; у
, F х ; у
F1 х0 a 2 b 2 ; у 0 , F2 х0 a 2 b 2 ; у 0
1
0
0
a2 b2
4.
Оси симметрии: прямые
5.
Асимптоты:
прямые y y 0
2
0
0
a2 b2
x x0 , y y 0 .
b
( x x0 ) и
a
для (а),
для (б);

32. Кривые второго порядка

Каноническое уравнение:
Кривые второго порядка
П
А
Р
А
Б
О
Л
А
Определение. Парабола – геометрическое место точек на
плоскости, равноудаленных от данной точки, называемой
фокусом, и данной прямой, называемой директрисой.
Каноническое уравнение:
y 2 2 px
или
x 2 2 py
где p 0 некоторое число,
называемое параметром
параболы.
Ось абсцисс Ox является
осью симметрии параболы.

33. Кривые второго порядка

П
А
Р
А
Б
О
Л
А
Свойства:
1. Вершина: О(0;0);
2.
3.
p
Фокусы параболы: F ;0 или
2
p
x
Директриса:
или
2
p
F 0;
2
p
y
2
Параболы, задаваемые уравнениями y y0
или
x x0
где
p
2
2
2 p x x0
2 p y y0 ,
некоторое число, называемое параметром параболы,
обладают свойствами:

34. Кривые второго порядка

;
П
А
Р
А
Б
О
Л
А
1. Вершина: точка О1 x0 ; y 0
2. Фокусы параболы:
3. Директриса:
4. Оси симметрии:
p
F х0 ; у 0 или
2
p
или
x х0
2
у у0
или
p
F х0 ; у 0
2
y у0
x x0
.
p
2

35. Кривые второго порядка

;
П
А
Р
А
Б
О
Л
А
Уравнение второй степени
Ax 2 Cy 2 2Dx 2Ey F 0, ( )
где числа А и С не равны одновременно нулю, преобразуется
к каноническому виду методом выделения полных квадратов и
последующим параллельным переносом.
Тип кривой определяется числами А и С:
1)
2)
3)
4)
Если А С , то ( )
– окружность;
если А С
и А С 0 то ( ) – эллипс;
если А С 0 , то ( ) – гипербола;
если одно из чисел А или С равно нулю, то – ( )
парабола.