Similar presentations:
Решение квадратных уравнений различными способами
1.
Решение квадратныхуравнений различными
способами
А.А. Вахрушев
Ученик МОУ СОШ № 32 8 «Г» класса
Л.Н. Радионова
Учитель математики МОУ СОШ № 32
2.
Если ты услышишь, что ктото не любит математику, неверь.
Её нельзя не
любить - её
можно только не
знать»
3.
Цель реферата:Научиться правильно отображать
формулы
с
применением
различных
способов
решения
уравнений
Задачи реферата:
- улучшить навыки решения уравнений;
наработать
новые
способы
решения
уравнений;
- выучить некоторые новые способы и формулы
для решения этих уравнений.
4.
История квадратных уравненийНеобходимость решать уравнения еще в древности была вызвана
потребностью решать задачи, связанные с нахождением
площадей земельных участков и с земельными работами военного
характера, а также с развитием астрономии и самой математики.
Решения этих уравнений, совпадает с современными.
Некоторые алгебраические приемы решения линейных и квадратных
уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Задачи на квадратные уравнения встречаются в 499 году составленные
индийским математиком и астрономом Ариабхаттой. Индийский ученый,
Брахмагупта (VII век), изложил общее правило решения квадратных
уравнений, приведенных к единой конической форме:
aх² + bx = c, где a > 0
Решения квадратных уравнений по образцу ал-Хорезми в Европе были
впервые изложены в «Книге абака», написанной в 1202 г. итальянским
математиком Леонардо Фибоначчи. Его книга способствовала
распространению алгебраических знаний не только в Италии, но и в
Германии, Франции и других странах Европы.
5.
Нестандартные способырешения уравнений
Решение уравнений
способом «переброски»
Решение квадратных
уравнений с помощью
циркуля и линейки
Свойства коэффициентов
квадратного уравнения
Геометрический способ
решения квадратных
уравнений
6.
Решение уравнений способом«переброски»
Этот способ применяют, когда можно легко найти корни уравнения,
используя теорему Виета и, что самое важное, когда дискриминант
есть точный квадрат.
ах2 + bх + с = 0, а ≠ 0
Умножая обе его части на а
Пусть ах = у, откуда x=
у
а
а2 х2 + а bх + ас = 0
Перейдем к
уравнению
у2 + by + ас = 0
корни у1 и у2 найдем с помощью теоремы Виета
полу
чим
у2
у1
х1 =
и х1 = .
а
а
7.
Свойства коэффициентов квадратногоуравнения
А. ах2 + bх + с = 0, а ≠ 0
1.Если а + b + с = 0, то х1 = 1, х2 =
с
а
Разделим обе части
уравнения на а ≠ 0
b c
x x 0
a a
2
b
х
х
Согласно теореме Виета 1 2
a по условию
х х c
1 2
a
откуда b a c
Таким
образом
a c
x
x
1 2
a
x x 1 c
1 2
a
получим
х1 1
a b c 0
c
и х2
a
8.
Свойства коэффициентов квадратногоуравнения
А. ах2 + bх + с = 0, а ≠ 0
2. Если a b c 0 или b a c , тох1 1 , х 2
по теореме
b
x
x
1
2
a
Виета
x x c
1 2
a
откуда b a c
Таким
образом
c
a
по условию a b c 0
a b
c
x
x
1
1 2
a
a
x1 x 2 1 c
a
получим
c
x1 1 и x 2
a
9.
Свойства коэффициентов квадратногоуравнения
Б. ах2 + bх + с = 0, а ≠ 0
Если второй коэффициент b = 2k – четное число, то
формулу корней х1,2 =
b b2 4ac
2a
х1,2 =
можно записать в виде
k k 2 ac
a
10.
Свойства коэффициентов квадратногоуравнения
В. уравнение x2 + px + q = 0 совпадает с уравнением
общего вида
где а = 1, p и c = q , то формула корней х1,2 =
х1,2 = p p 4q ,
2
Примет вид
2
b b2 4ac
2a
2
или
х1,2
p
p
q.
= - 2
2
11.
Решение квадратных уравнений спомощью циркуля и линейки
ах2 + bх + с = 0, а ≠ 0
По теореме о секущих имеем ОВ∙ОD = ОА ∙
ОС, откуда ОС =
Центр
ОВ ОD х1 х2 с
ОА
1
а
окружности находиться в точке
пересечения перпендикуляров SF и SK ,
восстановленных в серединах хорд AC
BD, поэтому
с
b
1
у
у
а с
х
х
b
SK = 1 2 а , SF = 1 2 а
2
2
2а
2
2
2а
С (0;
c
)
а
b a c
S ( 2a ; 2a )
F
и
А(0; 1)
В(х1, 0)
К
D(х2, 0)
12.
Решение квадратных уравнений спомощью циркуля и линейки
при этом возможны три случая
1. Радиус окружности больше ординаты
а с
),
2а
центра (AS > SK, или R >
окружность пересекает ось Ох в двух
точках B (х1 ; 0) и D (х2 ;0), где х1 и х2 –
корни квадратного уравнения
S
ах2 + bх + с = 0.
AS > SВ, или R >
A
B
а с
2а
Два решения х1 и х2
13.
Решение квадратных уравнений спомощью циркуля и линейки
2 случай
Радиус окружности равен ординате
центра (AS = SВ, или R =
а с
),
2а
окружность касается оси Ох в точке
B (х1 ; 0 ), где х1 – корень квадратного
уравнения.
S
A
B
AS = SВ, или R =
а с
2а
Одно решение х1
14.
Решение квадратных уравнений спомощью циркуля и линейки
3 случай
Радиус
окружности
меньше
ординаты центра (AS < SВ, или
R<
а с
),
2а
окружность не имеет общих
точек с осью абсцисс, в этом случае
S
уравнение не имеет решения.
A
B
AS < SВ, или R <
Нет решения
а с
2а
15.
Решение квадратных уравнений спомощью циркуля и линейки
при этом возможны три случая
1. Радиус окружности больше ординаты
а с
),
2а
центра (AS > SK, или R >
окружность пересекает ось Ох в двух
точках B (х1 ; 0) и D (х2 ;0), где х1 и х2 –
корни квадратного уравнения
S
ах2 + bх + с = 0.
AS > SВ, или R >
A
B
а с
2а
Два решения х1 и х2
16.
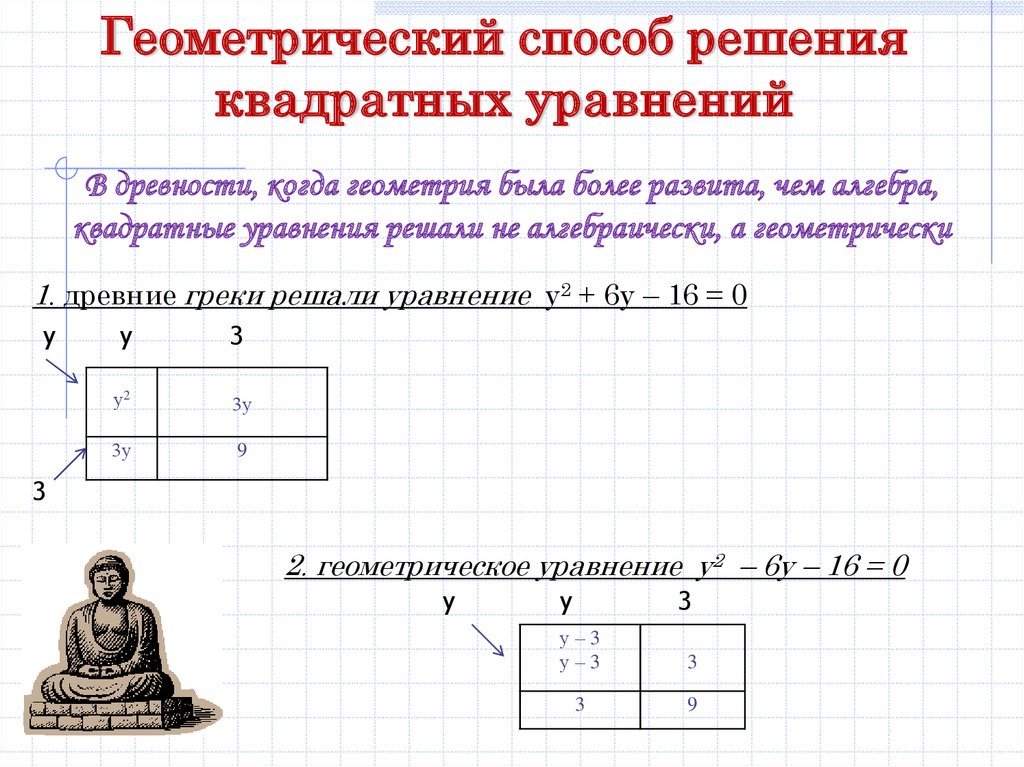
Геометрический способ решенияквадратных уравнений
В древности, когда геометрия была более развита, чем алгебра,
квадратные уравнения решали не алгебраически, а геометрически
1. древние греки решали уравнение у2 + 6у – 16 = 0
у
y
3
у2
3у
3у
9
3
2. геометрическое уравнение у2 – 6у – 16 = 0
у
y
3
у–3
у–3
3
3
9
17.
Квадратные уравнения находят широкоеприменение при решении
тригонометрических, показательных,
логарифмических, иррациональных и
трансцендентных уравнений и неравенств
Вывод:
Квадратные уравнения играют огромную
роль в развитии математики. Все мы
умеем решать квадратные уравнения со
школьной скамьи. Эти знания могут
пригодиться нам на протяжении всей
жизни
18.
методы решения квадратныхуравнений просты в применении, то
они, безусловно, должно
заинтересовать
увлекающихся
математикой
учеников
19.
Спасибо завнимание!


















 mathematics
mathematics








