Способы решения квадратных уравнений

1.

«Способы решения квадратных уравнений»

2.

Решение многих практических задач
сводится к решению квадратных уравнений.
Найдите катеты прямоугольного
треугольника, если известно, что
один из них на 4 см меньше
другого, а гипотенуза равна 20 см.
Тело брошено вертикально
вверх с начальной
скоростью 40м/с. Через
сколько секунд оно
окажется на высоте 60м?

3.

Из истории квадратных уравнений
Необходимость
решать
квадратные
уравнения
еще
в
древности была вызвана потребностью решать задачи,
связанные с нахождением площадей земельных участков, а
также с развитием астрономии и самой математики.
Найденные древние вавилонские глиняные
таблички (около 2 тысяч лет до н.э.)
являются самыми ранними свидетельствами
об изучении квадратных уравнений. Почти
все найденные до сих пор клинописные
тексты приводят только задачи с решениями,
изложенными в виде рецептов, без указаний
относительно того, каким образом они были
найдены.

4.

Индийский ученый Брахмагупта (VII в.),
изложил общее правило решения квадратных
уравнений, приведенных к единой форме:
ах2 + bх = с, а > 0
Правило Брахмагупта по существу совпадает
с нашим.
Брахмагупта
Формулы решения квадратных уравнений
в Европе были впервые изложены в 1202 г.
в «Книге абака» итальянским математиком
Леонардом Фибоначчи.
Леонардо Фибоначчи

5.

Лишь в XVII в. благодаря трудам Жирара, Декарта,
Ньютона и других ученых способ решения квадратных
уравнений принимает современный вид.
Я мыслю,
следовательно,
существую.
Декарт
Гений есть
терпение мысли,
сосредоточенной
в известном
направлении.
Ньютон
Все уравнения
алгебры имеют
столько решений,
сколько их
показывает
наименование
наивысшей
величины.
Жирар
Все математики
знали, что под
алгеброй были скрыты
несравненные
сокровища, но не
умели их найти
Виет

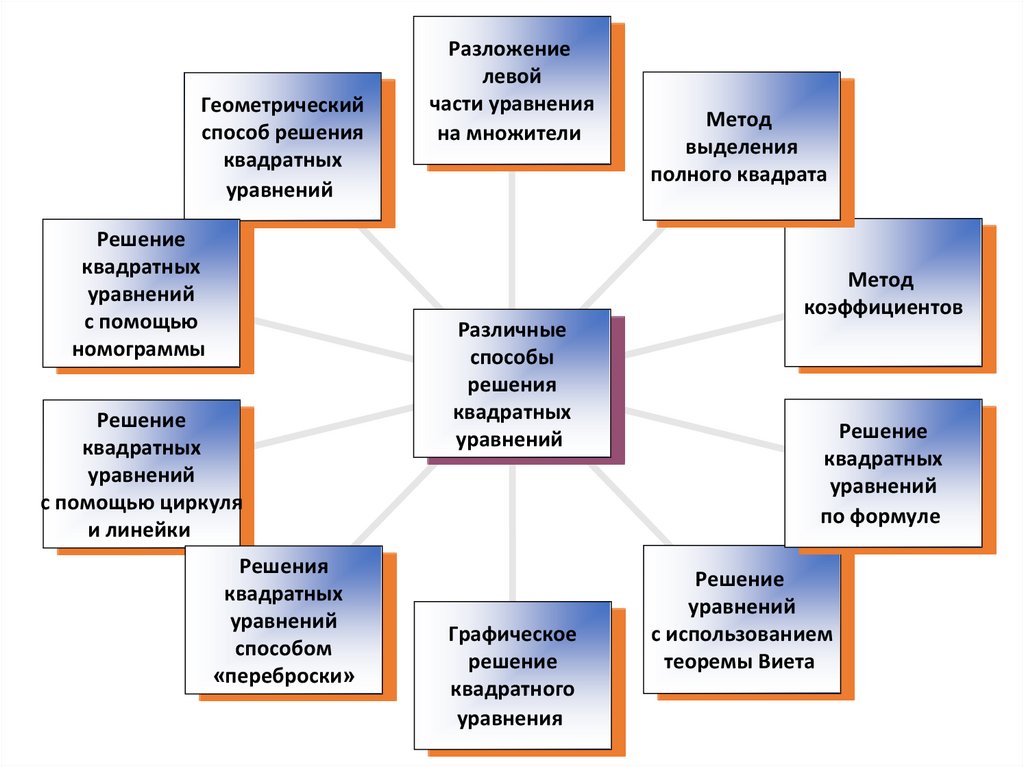
6.

Геометрический
способ решения
квадратных
уравнений
Решение
квадратных
уравнений
с помощью
номограммы
Решение
квадратных
уравнений
с помощью циркуля
и линейки
Решения
квадратных
уравнений
способом
«переброски»
Разложение
левой
части уравнения
на множители
Различные
способы
решения
квадратных
уравнений
Графическое
решение
квадратного
уравнения
Метод
выделения
полного квадрата
Метод
коэффициентов
Решение
квадратных
уравнений
по формуле
Решение
уравнений
с использованием
теоремы Виета

7.

В школьной программе мы изучаем всего несколько
различных способов решения квадратных уравнений:
1)Разложение левой части уравнения на множители.
2)Метод выделения полного квадрата.
3) Решение по формулам.
4) Формула для чётного коэффициента b.
5) Теорема Виета.
6) Графический способ решения квадратных уравнений.

8. Способ «переброски».

При этом способе коэффициент а умножается на свободный
член, как бы «перебрасывается» к нему, поэтому его называют
способом «переброски». Этот способ применяют, когда можно
легко найти корни уравнения, используя теорему Виета и, что
самое важное, когда дискриминант есть точный квадрат
Решим уравнение 2х2 – 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену, в
результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета у = 5, у =6, то х1 = 5/2, х = 6/2
Ответ: 2,5; 3.

9. Свойства коэффициентов квадратного уравнения

ах2 + bх + с = 0, где а ≠ 0.
Если, а+ b + с = 0 , то
c
x1 1, x2
a
Если b = a + c, то
c
x1 1, x2
a
1978 x 2 1984 x 6 0
x1 1;
6
x2
1978
319 x 2 1988 x 1669 0
x1 1;
1669
x2
.
319

10. Свойства коэффициентов квадратного уравнения

11. Свойства коэффициентов квадратного уравнения

12. Свойства коэффициентов квадратного уравнения

13. Свойства коэффициентов квадратного уравнения

14. Решение квадратных уравнений с помощью циркуля и линейки.

ах2 + bх + с =0
1) построим точки
(центр окружности) и A(0; 1);
2) проведем окружность с
радиусом SA;
3) абсциссы точек пересечения
этой окружности с осью Ох
являются корнями исходного
квадратного уравнения.
При этом возможны три случая.

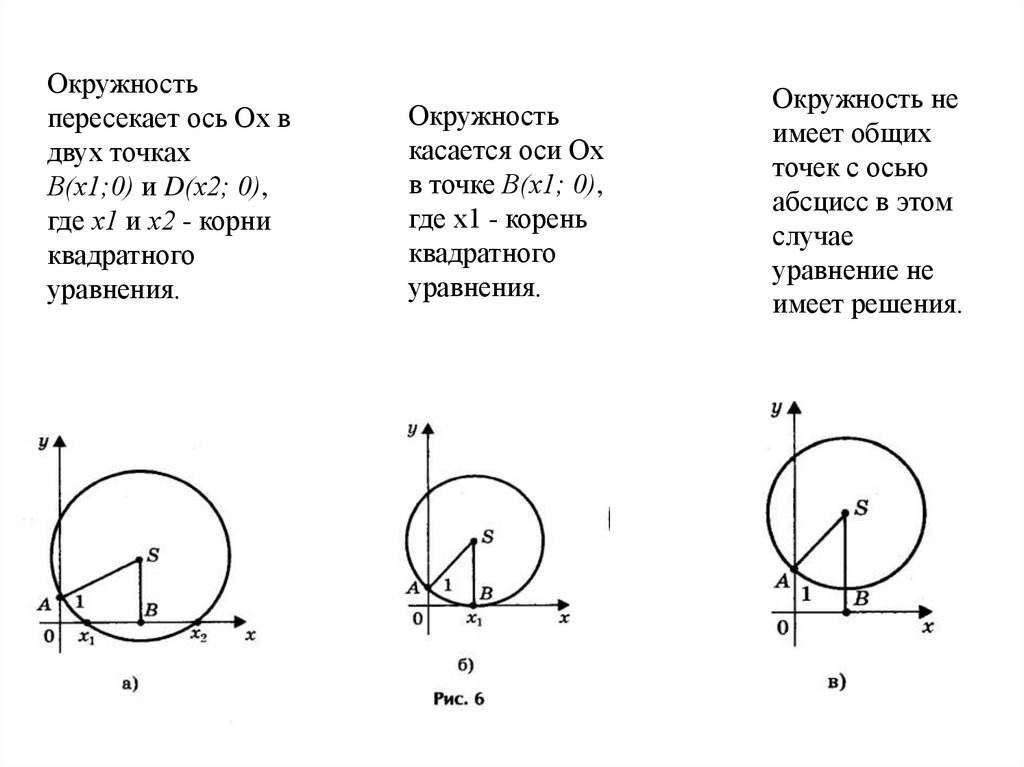
15.

Окружность
пересекает ось Ох в
двух точках
В(х1;0) и D(х2; 0),
где х1 и х2 - корни
квадратного
уравнения.
Окружность
касается оси Ох
в точке В(х1; 0),
где х1 - корень
квадратного
уравнения.
Окружность не
имеет общих
точек с осью
абсцисс в этом
случае
уравнение не
имеет решения.

16.

Пример. х2 - 2х - 3 = 0
Определим координаты точки центра
окружности по формулам:
Построим окружность радиуса SA, где А (0; 1).
Ответ: х1 = - 1; х2 = 3.

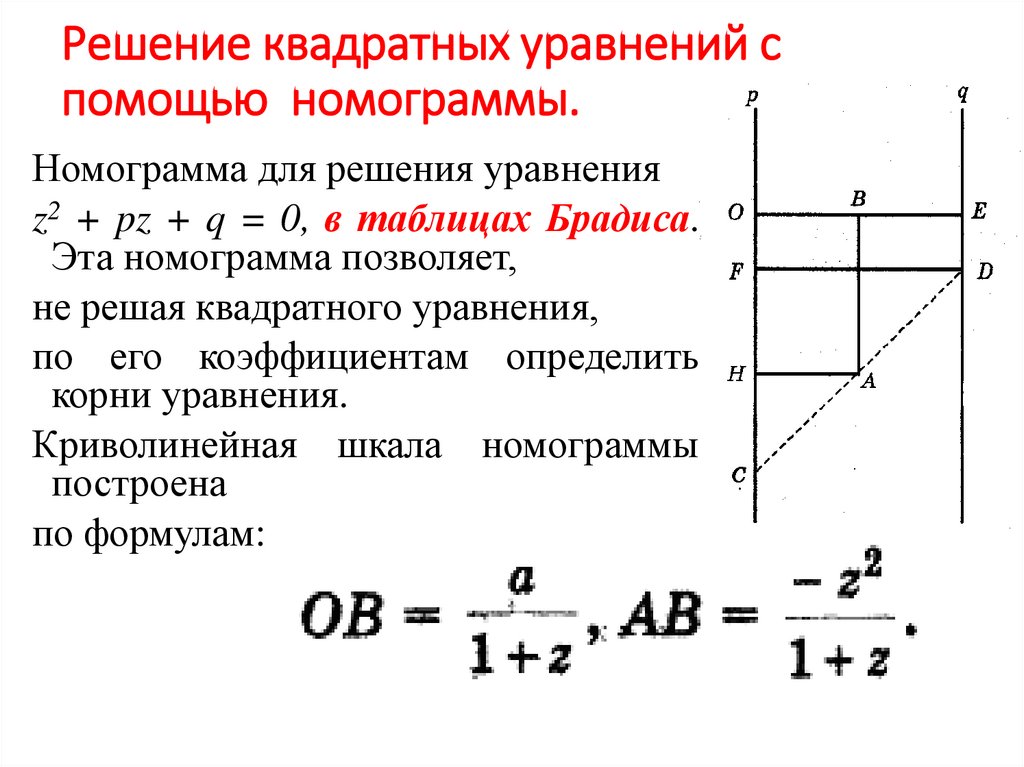
17. Решение квадратных уравнений с помощью номограммы.

Номограмма для решения уравнения
z2 + pz + q = 0, в таблицах Брадиса.
Эта номограмма позволяет,
не решая квадратного уравнения,
по его коэффициентам определить
корни уравнения.
Криволинейная шкала номограммы
построена
по формулам:

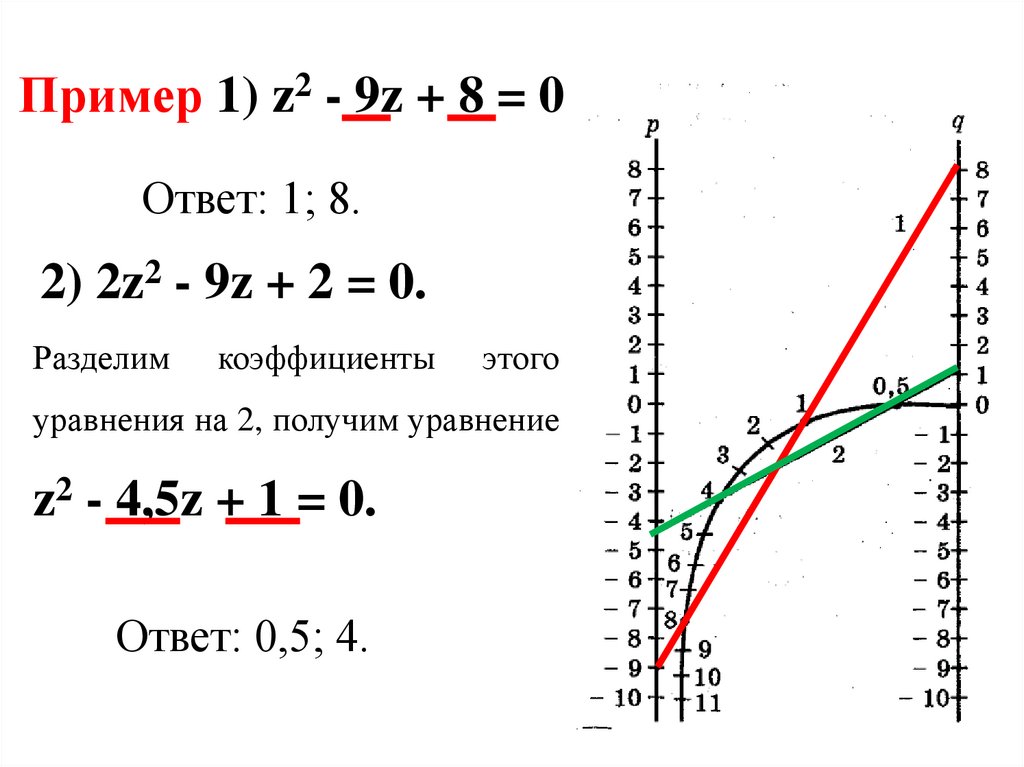
18.

Пример 1) z2 - 9z + 8 = 0
Ответ: 1; 8.
2) 2z2 - 9z + 2 = 0.
Разделим
коэффициенты
этого
уравнения на 2, получим уравнение
z2 - 4,5z + 1 = 0.
Ответ: 0,5; 4.

19.

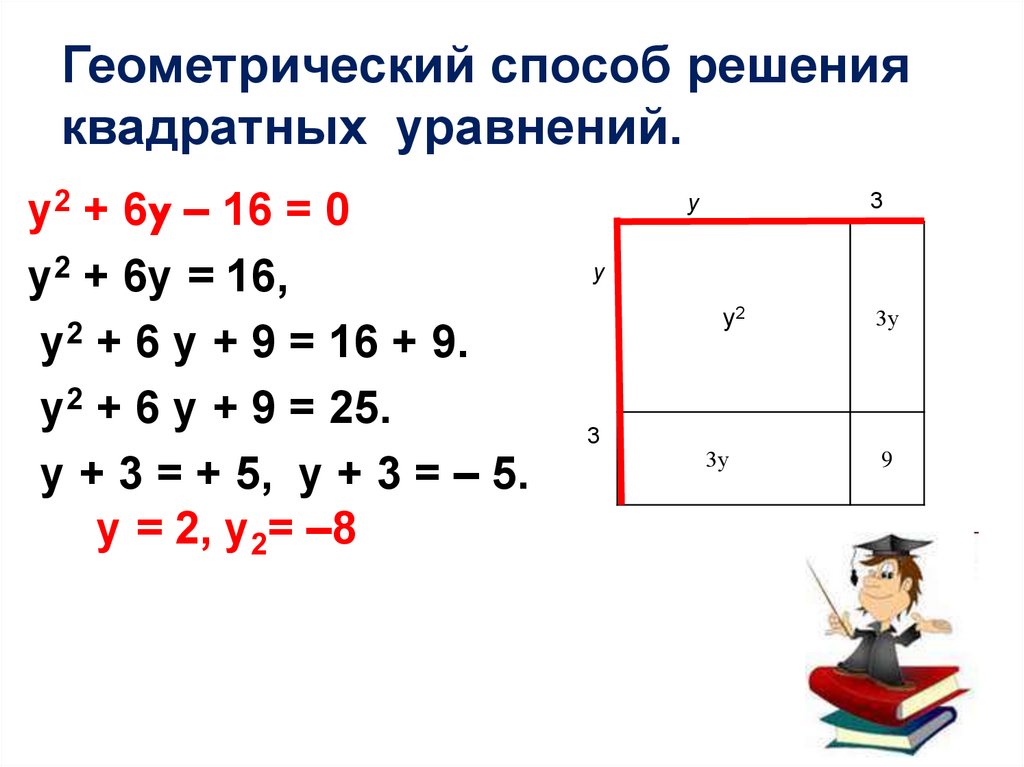
Геометрический способ решения
квадратных уравнений.
у2 + 6y – 16 = 0
у2 + 6у = 16,
у2 + 6 у + 9 = 16 + 9.
у2 + 6 у + 9 = 25.
у + 3 = + 5, у + 3 = – 5.
у = 2, у2= –8
у
3
у
у2
3
3у
3у
9