Способы решения квадратных уравнений

1.

2.

Исследовательская работа по теме:
Способы решения
квадратных уравнений

3.

Введение
Впервые мы услышали о квадратных уравнениях на уроке
математики от учителя. Особенно нас заинтересовали
способы их решения, причем наиболее рациональные.
Во-первых, очень удивило сочетание слов
«квадратное», «уравнение».
Во-вторых, чем знамениты эти уравнения.
В- третьих, почему их решением так долго занимались
великие ученые.
В-четвертых, способы решения квадратных
уравнений и их практическая значимость.
Эти вопросы нас очень заинтриговали, и мы решилип
проследить историю возникновения и решения данной
проблемы.

4.

Цели и задачи проекта.

5. Этапы исследования

История возникновения квадратных
уравнений.
Определение квадратного уравнения и его
виды.
Решение квадратных уравнений, используя
формулу дискриминанта .
Франсуа Виет и его теорема.
Свойства коэффициентов для быстрого
нахождения корней квадратного уравнения.
Практическая направленность.

6. 1 этап. История возникновения квадратных уравнений.

ОКАЗЫВАЕТСЯ:
Задачи на квадратные
уравнения встречаются уже в
499 г.
В Древней Индии были
распространены публичные
соревнования в решении
трудных задач –
ОЛИМПИАДЫ.

7. История возникновения квадратных уравнений.

Вот одна из задач знаменитого индийского
математика XII в. Бхаскары:
Обезьянок резвых стая
Всласть поевши,
развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А 12 по лианам…
Стали прыгать, повисая.
Сколько было обезьянок,
Ты скажи мне, в этой стае?

8.

Штифель (1486 – 1567) в 1544 году сформировал общее
правило решения квадратных уравнений, приведённых к
единому каноническому виду x2 + bx = c при
всевозможных комбинациях знаков и коэффициентов b и
c.
Франсуа Виет (1540 – 1603) вывел формулы решения
квадратного уравнения в общем виде, однако он
признавал только положительные числа.
Итальянские учёные Тарталья, Кардано, Бомбелли среди
первых в XVI веке учитывают, помимо положительных, и
отрицательные корни.
В XVII веке благодаря трудам Жиррара, Декарта, Ньютона и
других учёных, способ решения квадратных уравнений
принимает современный вид.

9.

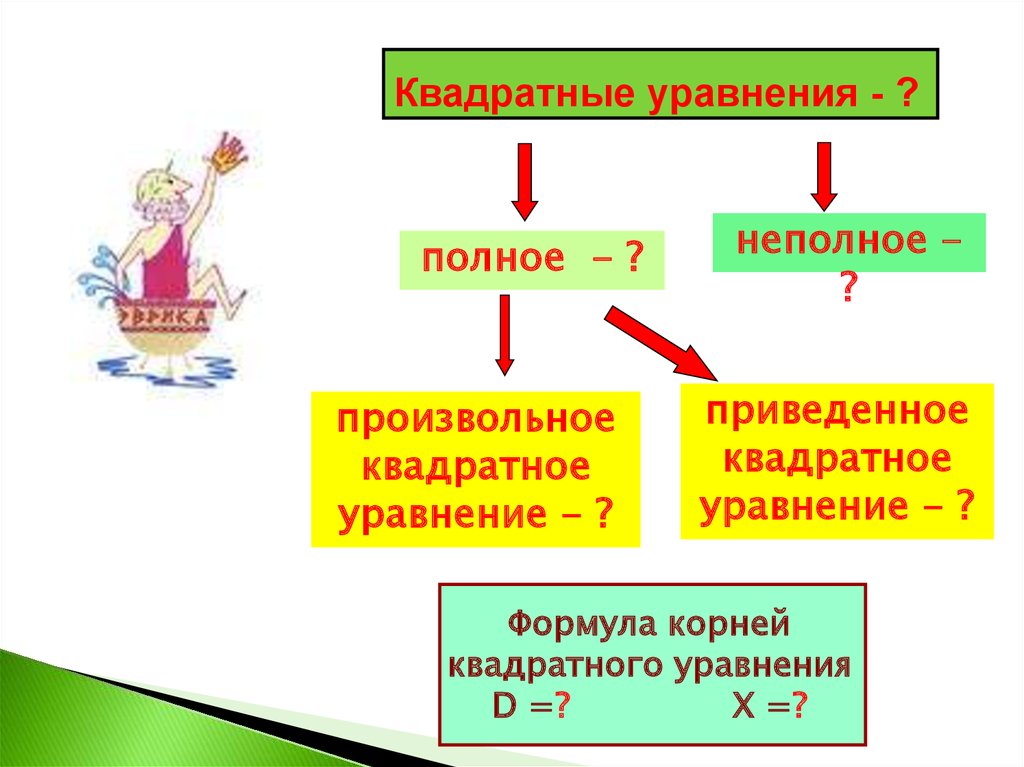
Квадратные уравнения - ?
полное - ?
произвольное
квадратное
уравнение - ?
неполное ?
приведенное
квадратное
уравнение - ?
Формула корней
квадратного уравнения
D =?
Х =?

10.

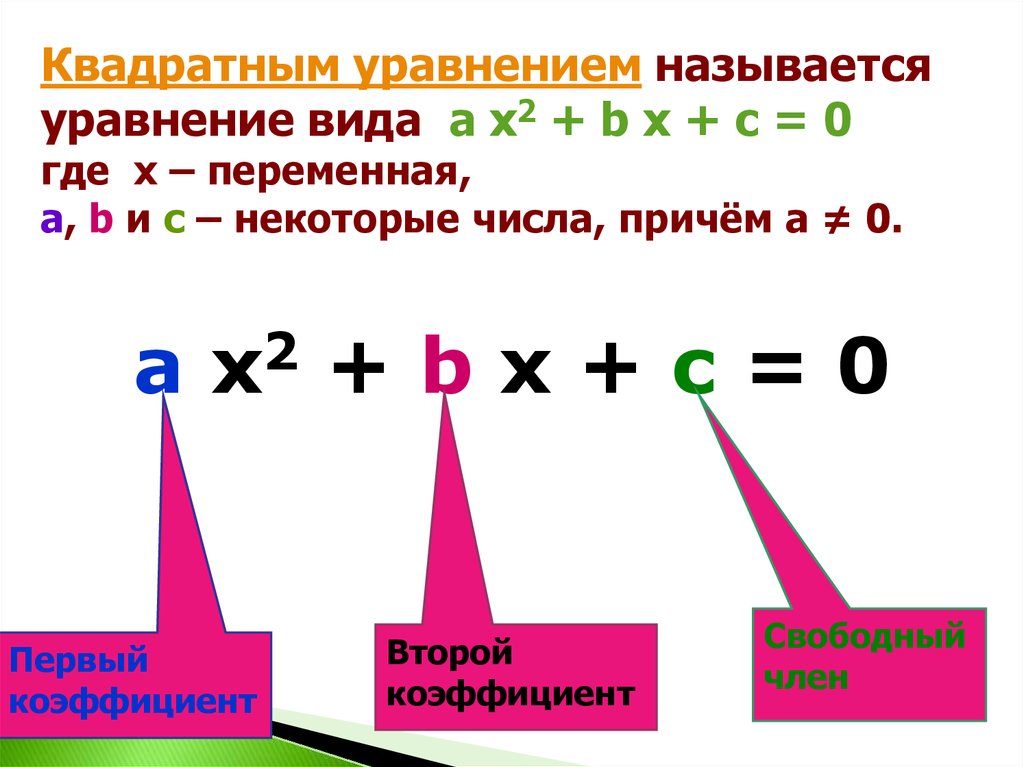
Квадратным уравнением называется
уравнение вида a х2 + b x + c = 0
где х – переменная,
a, b и c – некоторые числа, причём а ≠ 0.
a
2
x
Первый
коэффициент
+bx+c=0
Второй
коэффициент
Свободный
член

11.

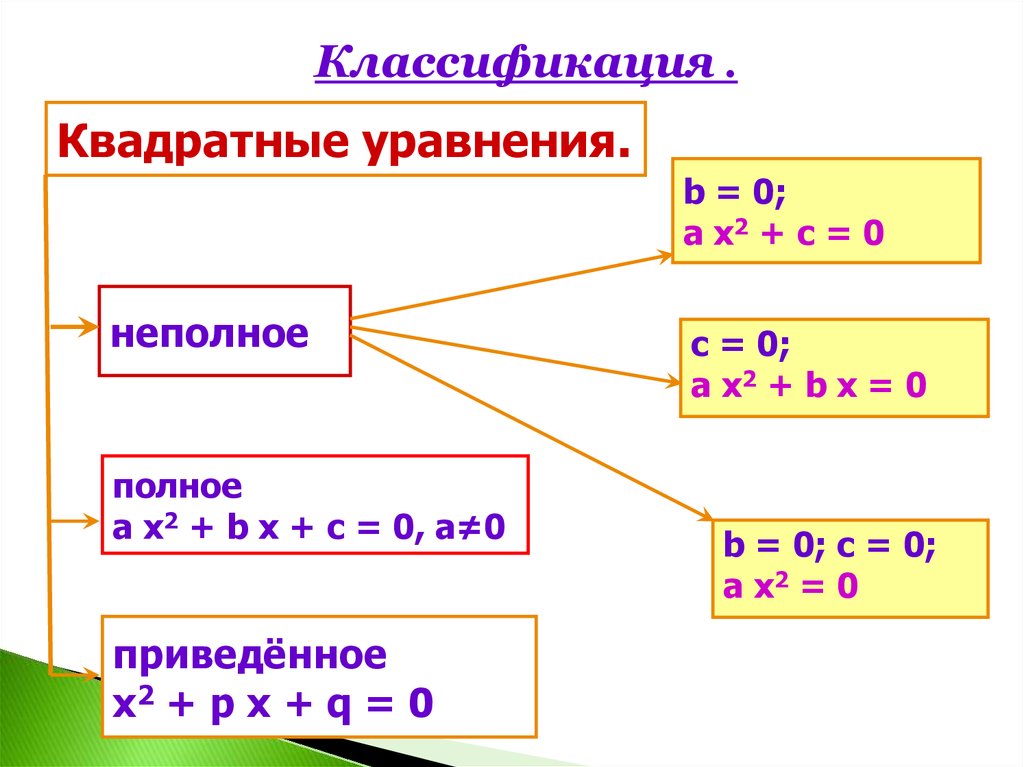
Классификация .
Квадратные уравнения.
b = 0;
a x2 + c = 0
неполное
полное
а х2 + b х + с = 0, а≠0
приведённое
x2 + p x + q = 0
c = 0;
a x2 + b x = 0
b = 0; c = 0;
a x2 = 0

12.

Решение полного квадратного уравнения.
a x2 + b x + c = 0
D = b2 – 4 ∙ а ∙ с
- «ДИСКРИМИНАНТ» - РАЗЛИЧИТЕЛЬ
D>0
Уравнение имеет
два действительных
корня.
D=0
Уравнение имеет
два равных
действительных
корня.
D<0
Уравнение не имеет
корней.
х1= (- b - √ D )/ 2а;
х2= (- b + √ D )/2а
х1,2 = - b / 2а

13.

2 этап. Провели исследование приведенных
квадратных уравнений, решив эти уравнения
№
1.
2.
3.
4.
5.
6.
Уравнение
х2 + х –12 = 0
х2 - 12х – 45 = 0
у2+ 8у +15 = 0
у2- 5у +6 = 0
z2-10z +21 = 0
z2- 3z -10 = 0
Корни
Сумма
уравнения корней
3 и –4
-1
Произведение
корней
-12
15 и -3
12
-45
-3 и –5
-8
15
2 и3
5
6
10
21
3
-10
3 и7
5 и -2
Нашли связь между коэффициентами а, b, с,
суммой и произведением корней квадратного
уравнения. Вывод:

14.

• Теорема Виета. Если корни х1 и х2
приведённого квадратного уравнения х2 + px
+ q = 0 , то х1 + х2 = - p, а х1 · х2 = q.
Обратное утверждение: Если числа m и
n таковы, что m + n = - p,
m∙n = q, то
эти числа являются корнями уравнения х2 +
px + q = 0.
Обобщённая теорема: Числа х1 и х2
являются корнями приведённого квадратного
уравнения х2 + px + q = 0 тогда и только
тогда, когда х1 + х2 = - p, х1 · х2 = q.
Следствие: х2 + px + q = (х – х1)(х – х2)

15.

Франсуа Виет
1540-1603
Французский математик,
ввел систему
алгебраических
символов, разработал
основы элементарной
алгебры. Он был одним
из первых, кто числа стал
обозначать буквами, что
существенно развило
теорию уравнений.
Виета часто называют«отцом
алгебры»

16.

Ситуации, в которых может
использоваться теорема Виета.
Проверка правильности найденных корней.
Определение знаков корней квадратного
уравнения.
Устное нахождение целых корней
приведённого квадратного уравнения.
Составление квадратных уравнений с
заданными корнями.
Разложение квадратного трёхчлена на
множители.

17.

Представляем задания из экзаменационных
материалов, которые легко решаются, зная
теорему Виета:
1.Верно ли, что числа 15 и 7 являются корнями
уравнения x2 – 22x + 105 = 0 ?
2.Определите знаки корней уравнения
x2 + 5x – 36 = 0.
2.Найдите устно корни уравнения x2 – 9x + 20
= 0.
3.Составьте квадратное уравнение, корнями
которого являются числа 1/3 и 0,3.
5. Разложите квадратный трёхчлен
x2 + 2x –
48
на множители.

18.

Мы решали квадратные
уравнения различными
способами:
1. выделением квадрата
двучлена, по формуле
корней,
2. с помощью теоремы
Виета, и каждый раз
убеждались в том,
что уравнение можно
решить
легче
и
Оказывается, есть ещё
быстрее.
другие
способы решения
квадратных уравнений,

19.

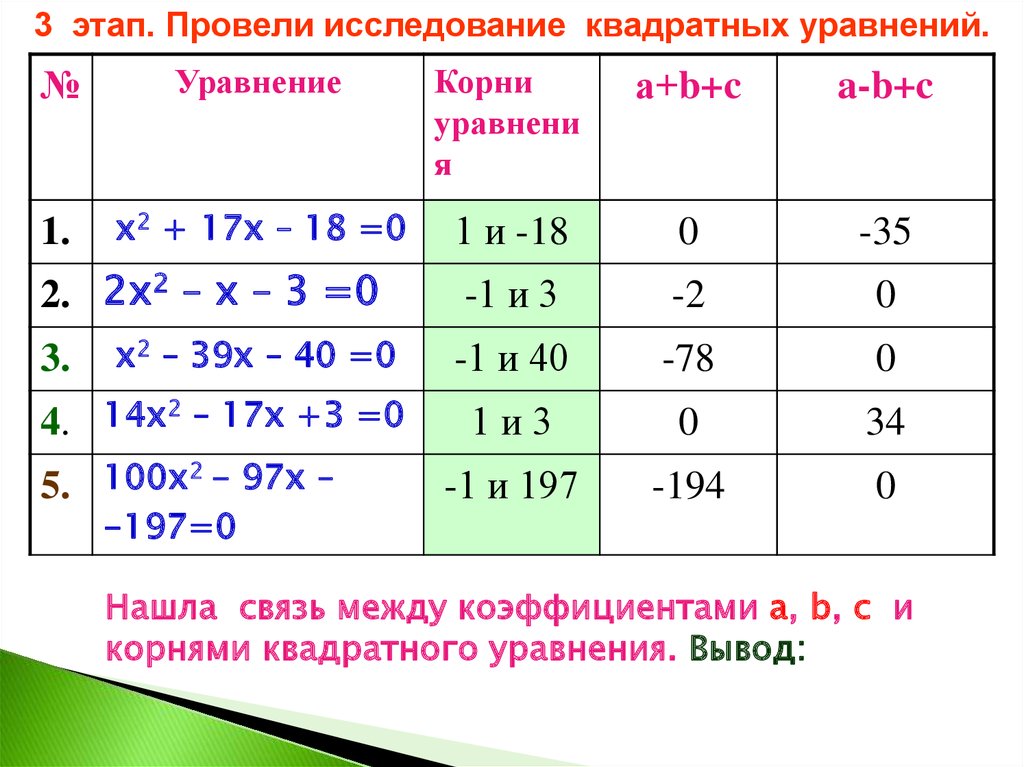
3 этап. Провели исследование квадратных уравнений.
№
Уравнение
Корни
уравнени
я
а+b+c
a-b+c
1.
х2 + 17х – 18 =0
1 и -18
0
-35
-1 и 3
-2
0
-1 и 40
-78
0
1и3
0
34
-1 и 197
-194
0
2. 2х2 – х – 3 =0
3.
х2 – 39х – 40 =0
4. 14х2 – 17х +3 =0
5. 100х2 - 97х –
-197=0
Нашла связь между коэффициентами а, b, с и
корнями квадратного уравнения. Вывод:

20.

Свойство 1.
Если в уравнении ах2 + bх +с = 0, а + b + с = 0,
то один из его корней равен 1, а другой, в
соответствии с теоремой Виета, равен с/а.
Пример: х2 + х – 2 = 0 ;
, с = -2
х2 = -2
1+1–2=0
а=1 , в=1
;
х1 = 1 ,
Свойство 2.
Если в уравнении ах2 + bх + с = 0, а – b +
с = 0 или b=a+c, то один из его корней
равен –1, а другой –с/а
Пример : х2 – х – 2 = 0,
1 – (- 1 ) + ( -2 ) = 0,
х1 = -1, х2 = 2

21.

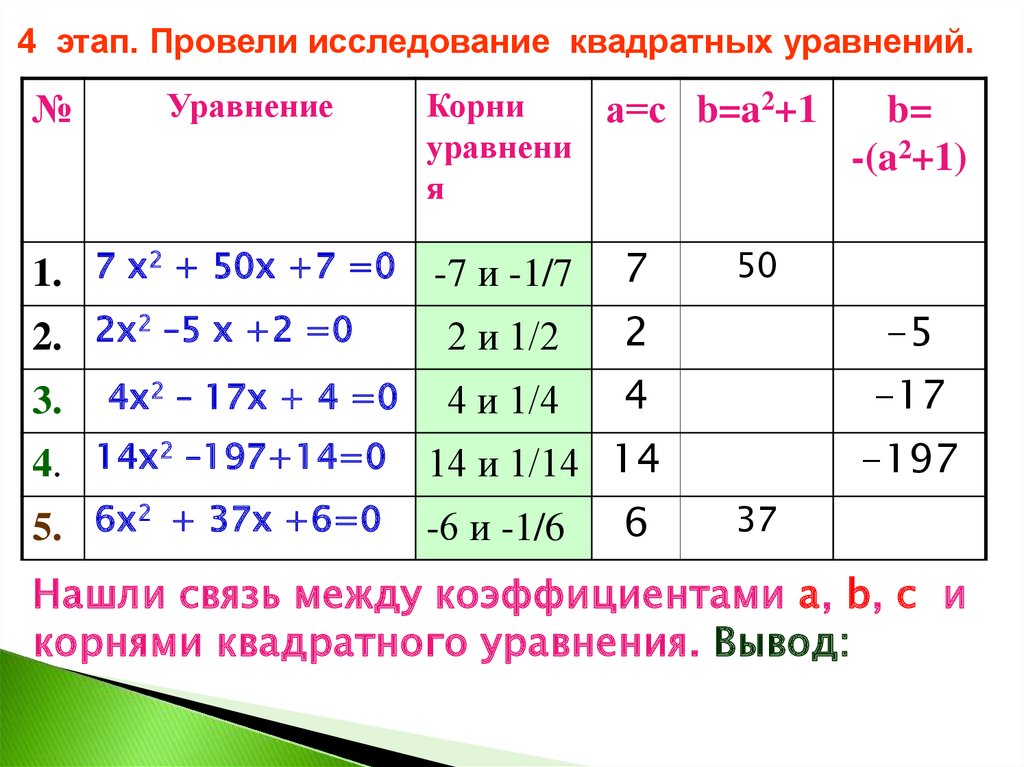
4 этап. Провели исследование квадратных уравнений.
№
Уравнение
Корни
а=с b=a2+1
b=
уравнени
-(a2+1)
я
1. 7 х2 + 50х +7 =0 -7 и -1/7
7
2. 2х2 –5 х +2 =0
2 и 1/2
2
-5
4 и 1/4
4
-17
3.
4х2 – 17х + 4 =0
4. 14х2 –197+14=0
5. 6х2 + 37х +6=0
14 и 1/14 14
-6 и -1/6 6
50
-197
37
Нашли связь между коэффициентами а, b, с и
корнями квадратного уравнения. Вывод:

22.

Свойство 3.
Если a = c, b = a2 + 1, то x1 = - a, а
x2 = -1/a.
Пример. 3х2+10х+3=0,
а=3, b=10, с=3.
Так как а=с=3, b=32+1=10, то
х1=-3, х2=1/3
Свойство 4.
Если a = c, b = -(a2 + 1), то x1 = a, а
x2 = 1/a.
Пример. 3х2 - 10х+3=0,
а=3,b=-10,с=3.
Так как а=с=3, b=-(32+1)=-10, то
х1=3, х2=1/3

23.

6 x 2 7 x 3 0 x 2 7 x 18 0
Корни 9 и (-2).
Делим числа 9 и ( -2) на 6:
9
2
x1 , x 2
6
6
Ответ:
3 1
;
2 3

24.

Вывод:
1. Проводя исследование, выяснили, что кроме
традиционных методов решения квадратного
уравнения , которые мы узнали на уроках алгебры,
существуют еще не менее интересные, а главные
полезные свойства, практически устного решения
квадратного уравнения.
2. Исследовательскую работу по математике
планируем продолжать и далее.
3. Результаты своего исследования мы представили в
виде карточки-памятки по решению квадратного
уравнения.