Similar presentations:
Квадратные уравнения (методы решения)
1.
Если ты услышишь, что ктото не любит математику, не верь.Её нельзя не любить - её можно
только не знать.
2. Квадратные уравнения
(методы решения)3. Азбука квадратного уравнения
ax bx c 02
(a 0)
4. Неполные квадратные уравнения:
ax 0x 0
ax bx 0,
x 0
2
2
b 0
ax
2
c 0,
c 0
b
x
a
Если c < 0, то корней нет
a
Если c > 0, то x
a
c
a
5.
ax bx c 02
D b 4ac
2
D<0
Корней
нет
D=0
D>0
b
x
2a
b D
x
2a
6.
ax bx c 02
b = 2k (четное число)
b
D1
2
2
ac
b
2
x
a
D1 0
D1
7. Теорема Виета
x1 и х2 – корниеслиуравнения
2
x px q 0 ( D 0)
то x1 x 2 p
x1 x 2 q
если
x1 и х2 – корни
уравнения
ax 2 bx c 0
то
x1 x 2
x1 x 2
c
a
( D 0)
b
a
8. Решите уравнения
5x2 = 15x3x2 - 75 = 0
x2- 7x + 12 = 0
5x2- 7x - 6 = 0
9. Проверка
Уравнениеa
b
c
x1
x2
x1+ x2
x 1 · x2
x2- 7x + 12 = 0
1
-7
12
4
3
7
12
5x2- 7x - 6 = 0
5
-7
-6
2
-0,6
1,4
-1,2
5x2 = 15x
5
-15
0
0
3
3x2 - 75 = 0
3
0
-75
5
-5
b2 - 4ac
169
10. Специальные методы:
1. Метод выделения квадратадвучлена.
2. Метод «переброски» старшего
коэффициента
3. На основании теорем:
Далее
11.
Метод выделения квадратадвучлена.
Цель: привести квадратное уравнение
общего вида к неполному
квадратному уравнению.
Пример:
x 6x 8 0
2
12.
Метод «переброски» старшегокоэффициента.
Корни квадратных уравнений
ax bx c 0
2
и
y 2 by ac 0
связаны соотношениями
y1
x1
a
и
x2
y2
a
В некоторых случаях бывает удобно решать сначала не
данное квадратное уравнение, а приведенное,
полученное «переброской» коэффициента а .
Пример:
2x 9x 5 0
2
13. На основании теорем:
Если в квадратном уравнении a+b+c=0, тоодин из корней равен 1, а
c
второй по теореме Виета равен a
Если в квадратном уравнении a+c=b, то
один из корней равен -1,
c
а второй по теореме Виета равен
a
Примеры:
157 x 20 x 177 0
2
203x 220 x 17 0
2
14. Общие методы:
Разложение на множители;Введение новой переменной;
Графический метод.
Далее
15. Метод разложения на множители
Цель:привести квадратное уравнение
общего вида к виду
А(х)·В(х)=0,
где А(х) и В(х) – многочлены
относительно х.
Способы:
Вынесение общего множителя за скобки;
Использование формул сокращенного умножения;
Способ группировки.
Пример:
3x 2 2 x 1 0
16. Введение новой переменной.
Умение удачно ввести новую переменную –важный элемент математической культуры.
Удачный выбор новой переменной делает
структуру уравнения более прозрачной.
Пример:
5 x 3
2
3 5 x 3 2
17. Решение уравнений с отрицательными дискриминантами
Решение уравнений сотрицательными дискриминантами
i2 = — 1.
Решите уравнение
x2 + 2х + 5 = 0
18.
В Древней Индии были распространены публичныесоревнования в решении трудных задач. Задачи
часто облекались в стихотворную форму.
________________________________________________
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши,
развлекалась.
Их в квадрате часть восьмая на полянке
забавлялась.
А двенадцать по лианам стали прыгать,
повисая.
Сколько ж было обезьянок, ты скажи мне, в этой
стае?
19.
Решение задачи Бхаскары:Пуст ь было
x
обезьянок,
тогда на поляне забавлялось –
x
8
2
Сост авим 2уравнение:
x
8
+
12 = х
От вет : х1= 16 , х2= 48 обезьянок.
.




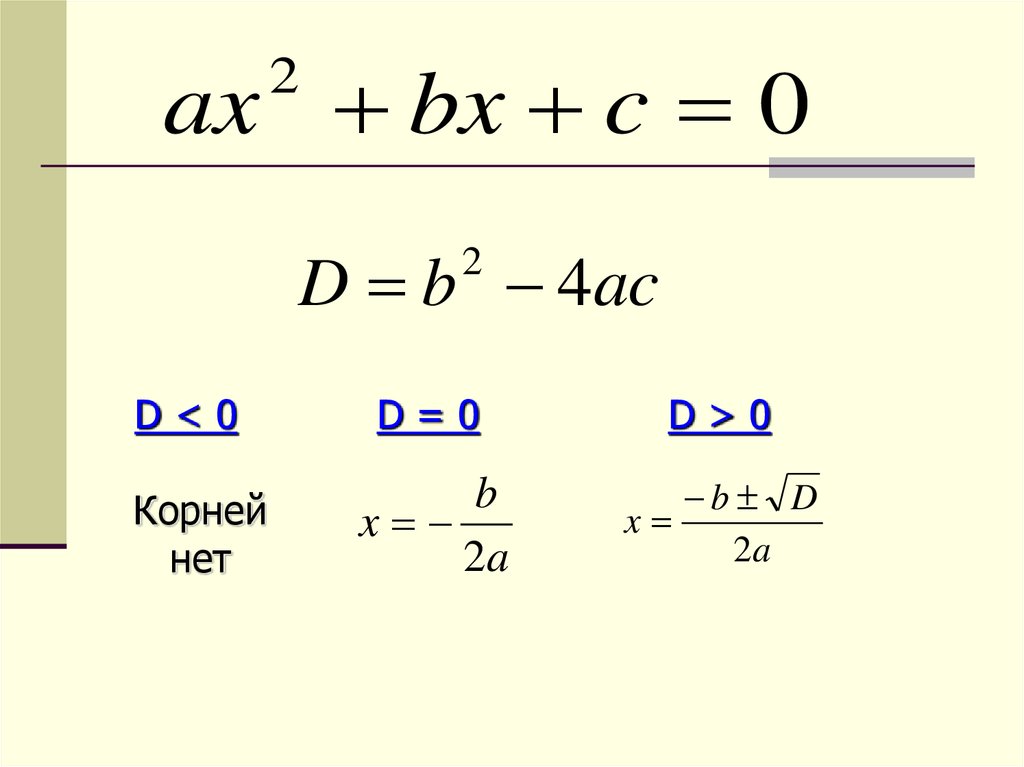
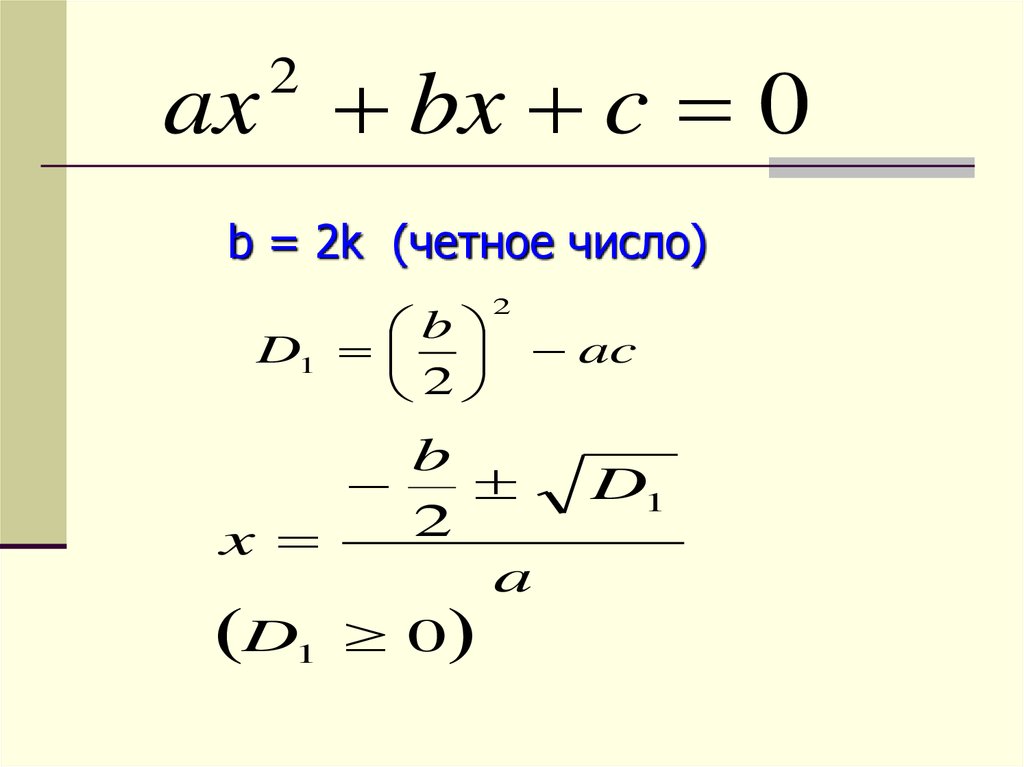













 mathematics
mathematics








