Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена

1. Двадцать восьмое февраля Тема: Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой

9 класс
АЛГЕБРА
Двадцать восьмое февраля
Тема: Понятие числовой последовательности.
Задание последовательности рекуррентной
формулой и формулой n-го члена.

2.

Термин «последовательность» используют, когда говорят о расположении
учеников в шеренге, очередности дней недели, расположении команд в
турнирной таблице и т.д. На сегодняшнем уроке мы выясним, что такое
числовая последовательность.
Мы сталкиваемся с последовательностями чисел каждый день. Вот только
встреча с последовательностями на экзамене может быть не самой
приятной. Чтобы было иначе, вы должны сегодня изучить урок очень-очень
внимательно.

3.

4. В рассмотренных примерах мы имели дело с последовательностями, содержащими бесконечно много членов. Такие последовательности

называются бесконечными.
Заметим, что последовательность может содержать конечное число
членов. В таком случае ее называют конечной.

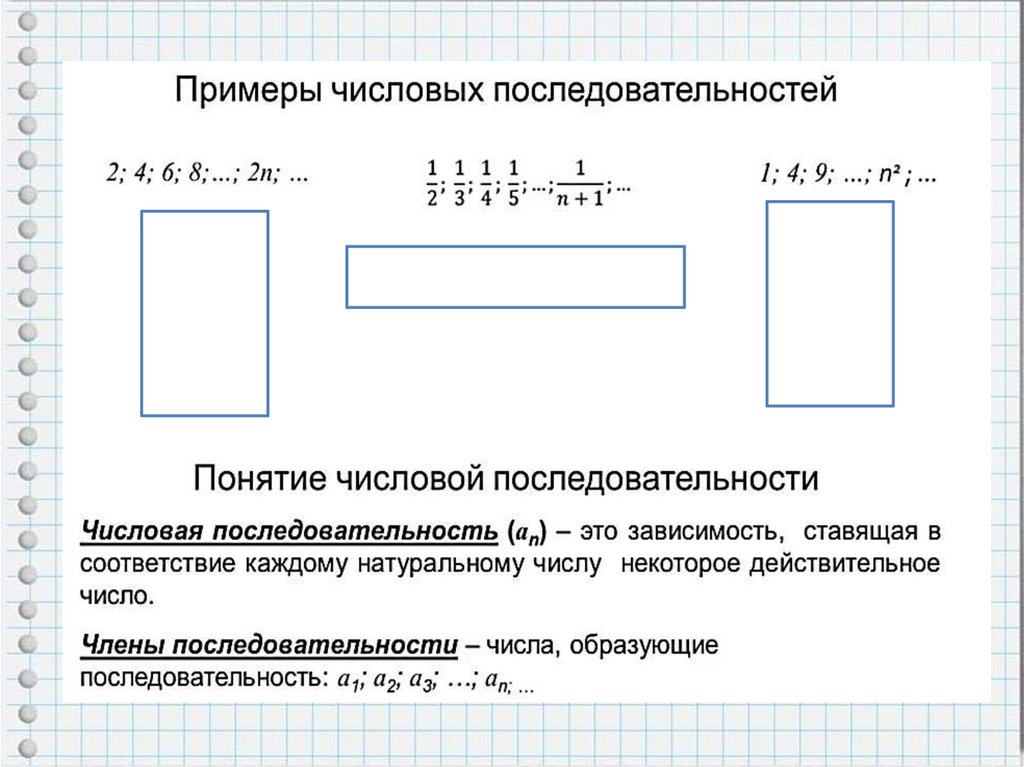
5. Способы задании последовательностей

Чтобы задать последовательность, нужно указать способ,
позволяющий найти член последовательности с любым номером.
Часто последовательность задают с помощью
формулы n-го члена последовательности.

6. Пример 1.

Пусть последовательность задана формулой уn = n2 - 3n.
Подставляя вместо n натуральные числа 1, 2, 3, 4, 5 и т. д.,
получаем y1 = -2, у2 = -2, у3 = 0, у4 = 4, у5 = 10, ... .
Рассматриваемая последовательность начинается так:
-2; -2; 0; 4; 10; ... .
Пример 2.
Пусть последовательность задана формулой хn = (-1)n • 10.
Все члены этой последовательности с нечетными номерами
равны -10, а с четными номерами равны 10:
х1 = -10, х2 = 10, х3 = -10, х4 = 10, ... .
Получаем последовательность:
-10; 10; -10; 10; -10; ... .

7.

Пример 3.
Пример 4.

8.

Рассмотрим еще один способ задания последовательности. Он состоит в
том, что указывают ее первый член или первые несколько членов и
формулу, выражающую любой член последовательности, начиная с
некоторого, через предыдущие (один или несколько).
Такую формулу называют рекуррентной (от латинского слова recurro —
возвращаться), а соответствующий способ задания последовательности
— рекуррентным способом.
Пример 4.
Пример 5.

9.

Пример 6.
Пусть (un) — последовательность, в которой
n1 = 1,
u2 = 1,
un + 1 = un + un -1 при n > 2.
Выпишем первые несколько ее членов: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Эта последовательность описана в работах итальянского математика
Леонардо из Пизы, известного под именем Леонардо Фибоначчи
(1180—1240).
Члены этой последовательности называют числами Фибоначчи.

10.

Домашнее задание
Посмотрите видеоурок:
Числовая последовательность. Что это? | Алгебра 9 класс - поиск
Яндекса по видео (yandex.ru)
По учебнику прочитать п. 24, выучить правила, решите
задания

11.

СПАСИБО
ЗА ВНИМАНИЕ

12. Использованные ремурсы:

• https://file.11klasov.net/1384-algebra-9-klass-uchebnik-makarychev-yun-mindyukng-i-dr.html
• http://лена24.рф/Алгебра_9_кл_Макарычев/24.html
• https://interneturok.ru/lesson/algebra/9-klass/progressii/chislovaya-posledovatelnosti-sposoby-ee-zadaniya
• https://www.evkova.org/chislovyieposledovatelnosti#Числовые%20последовательности
• https://zaochnik.ru/blog/chislovye-posledovatelnosti-dlja-chajnikov/