Similar presentations:
Пределы. Понятие числовой последовательности
1.
2. Понятие числовой последовательности
Рассмотрим ряд натуральных чисел N:1, 2, 3, …, n – 1, n, п + 1, …
Функцию y = f(x), x N называют функцией натурального
аргумента или числовой последовательностью и обозначают
y = f(n) или y1, y2, …, yn, … или {уn}.
Величина уn называется общим членом последовательности.
Обычно числовая последовательность задаётся некоторой
формулой уn = f(n), позволяющей найти любой член
последовательности по его номеру n;
эта формула называется формулой общего члена.
3. Примеры числовых последовательностей
Примеры числовых последовательностей1, 2, 3, 4, 5, … – ряд натуральных чисел;
2, 4, 6, 8, 10, … – ряд чётных чисел;
1, 4, 9, 16, 25, … – ряд квадратов натуральных чисел;
5, 10, 15, 20, … – ряд натуральных чисел, кратных 5;
1, 1/2, 1/3, 1/4, 1/5, ... – ряд вида 1/n, где n N;
и т.д.
4. Способы задания последовательностей
1. Перечислением членов последовательности (словесно).2. Заданием аналитической формулы.
3. Заданием рекуррентной формулы.
Примеры:
1. Последовательность простых чисел:
2; 3; 5; 7; 11; 13; 17; 19; 23; 29; …
2. Арифметическая прогрессия:
an = a1 + (n – 1)d
3. Геометрическая прогрессия:
bn + 1 = bn ∙ q
5. Ограниченность числовой последовательности
Последовательность {уn} называют ограниченнойсверху, если все ее члены не больше некоторого числа.
Последовательность {уn} ограниченна сверху, если
существует число M такое, что для любого п
выполняется неравенство
уп ≤ М
Число
М
называют
верхней
границей
последовательности.
Пример: -1, -4, -9, -16, …, -п2, … - ограничена сверху 0.
6. Ограниченность числовой последовательности
Последовательность {уn} называют ограниченной снизу, есливсе ее члены не меньше некоторого числа.
Последовательность
{уn}
ограниченна
снизу,
если
существует число m такое, что для любого п
выполняется неравенство
уп ≥ m
Число m называют нижней границей последовательности.
Пример: 1, 4, 9, 16, …, п2, … - ограничена снизу 1.
Если последовательность ограничена и сверху и снизу,
то ее называют ограниченной последовательностью.
7. Возрастание и убывание числовой последовательности
Последовательность {уn} называют возрастающейпоследовательностью, если каждый ее член больше
предыдущего:
у1 < y2 < y3 < y4 < … < yn < yn+1 < …
Пример: 1, 3, 5, 7, 9, 2п – 1, … - возрастающая
последовательность.
Последовательность {уn} называют убывающей
последовательностью, если каждый ее член
меньше предыдущего:
у1 > y2 > y3 > y4 > … > yn > yn+1 > …
Пример: 1, 1/3, 1/5, 1/7, 1/(2п – 1), … - убывающая
последовательность.
Возрастающие и убывающие последовательности
называют монотонными
8. Предел числовой последовательности
Рассмотрим числовую последовательность, общий член которойприближается к некоторому числу a при увеличении
порядкового номера n.
В этом случае говорят, что числовая последовательность
имеет предел. Это понятие имеет более строгое определение.
Число а называется пределом числовой последовательности {un}
если для любого ε > 0 найдется такое число N = N(ε), зависящее
от ε, что │un – a│< ε при n > N
lim un a
n
9. Предел числовой последовательности
Это определение означает, что a есть предел числовойпоследовательности, если её общий член неограниченно
приближается к a при возрастании n. Геометрически это
значит, что для любого ε > 0 можно найти такое число
N, что начиная с n > N все члены последовательности
расположены внутри интервала (a – ε, a + ε).
Последовательность, имеющая предел, называется
сходящейся; в противном случае – расходящейся.
10. Рассмотрим последовательность:
1;1 1 1 1
1
; ; ; ; ...; ; ... – гармонический ряд
2 3 4 5
n
Если m N, k R, то lim
k
n n
m
1
0
n n
lim
0
n
lim
q
0
Если │q│< 1, то
n
Если │q│> 1, то последовательность уn = q
n
расходится
11. Свойства пределов
Еслиlim хn b
n
, то lim yn с
n
1. предел суммы равен сумме пределов:
lim хn уn b c
n
2. предел произведения равен произведению пределов:
lim хn уn bc
n
3. предел частного равен частному пределов:
хn
lim
n у n
b
с
4. постоянный множитель можно вынести за знак предела:
lim kхn kb
n
12. Примеры:
1) lim1
n n 2
1
1
1 1
lim lim lim 0 0 0
n n n
n n n n
2
5
2 5
2) lim 2 3 lim lim 2 lim 3 0 0 3 3
n n
n
n
n n n n
1
1
1
1 1
lim
...
lim
...
lim
0 ... 0 0
k
n n
n n n
n n n n n
3) lim
1
2n 2
3
3
2
2
2
2
2n 2 3
n
n
n
lim
4) lim 2
lim
4
n n 4
n n 2
n
4
1
2 2
2
n
n
n
3
lim 2 lim 2
n
n n
2 0
2
4 1 0
lim 1 lim 2
n
n n
lim 2 3
2
n
n
4
lim 1 2
n
n
13.
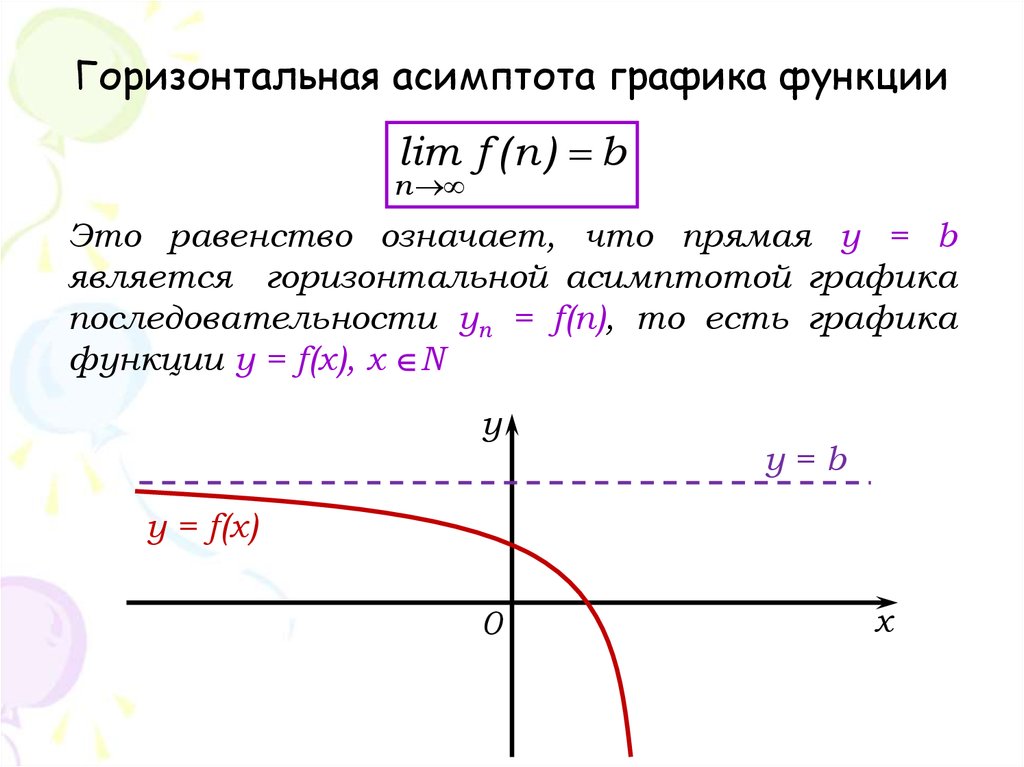
Горизонтальная асимптота графика функцииlim f ( n ) b
n
Это равенство означает, что прямая у = b
является горизонтальной асимптотой графика
последовательности yn = f(n), то есть графика
функции y = f(х), х N
у
у=b
y = f(x)
0
х
14.
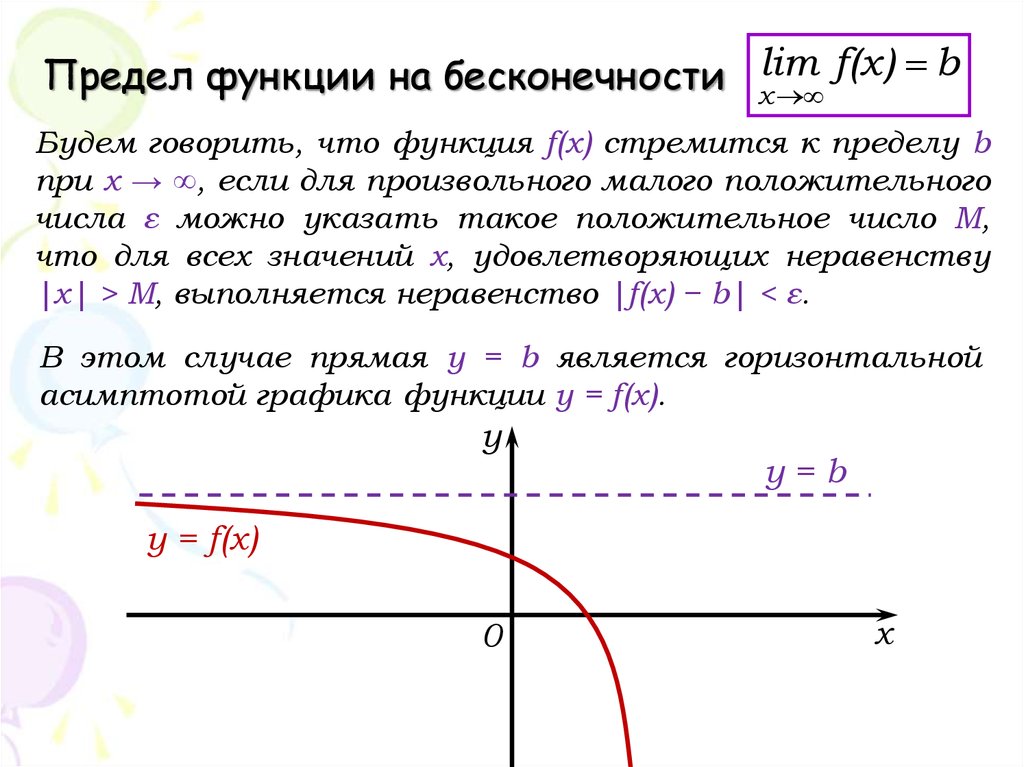
15. Предел функции на бесконечности
f(x) bПредел функции на бесконечности xlim
Будем говорить, что функция f(x) стремится к пределу b
при x → ∞, если для произвольного малого положительного
числа ε можно указать такое положительное число M,
что для всех значений x, удовлетворяющих неравенству
|x| > M, выполняется неравенство |f(x) − b| < ε.
В этом случае прямая у = b является горизонтальной
асимптотой графика функции y = f(x).
у
у=b
y = f(x)
0
х
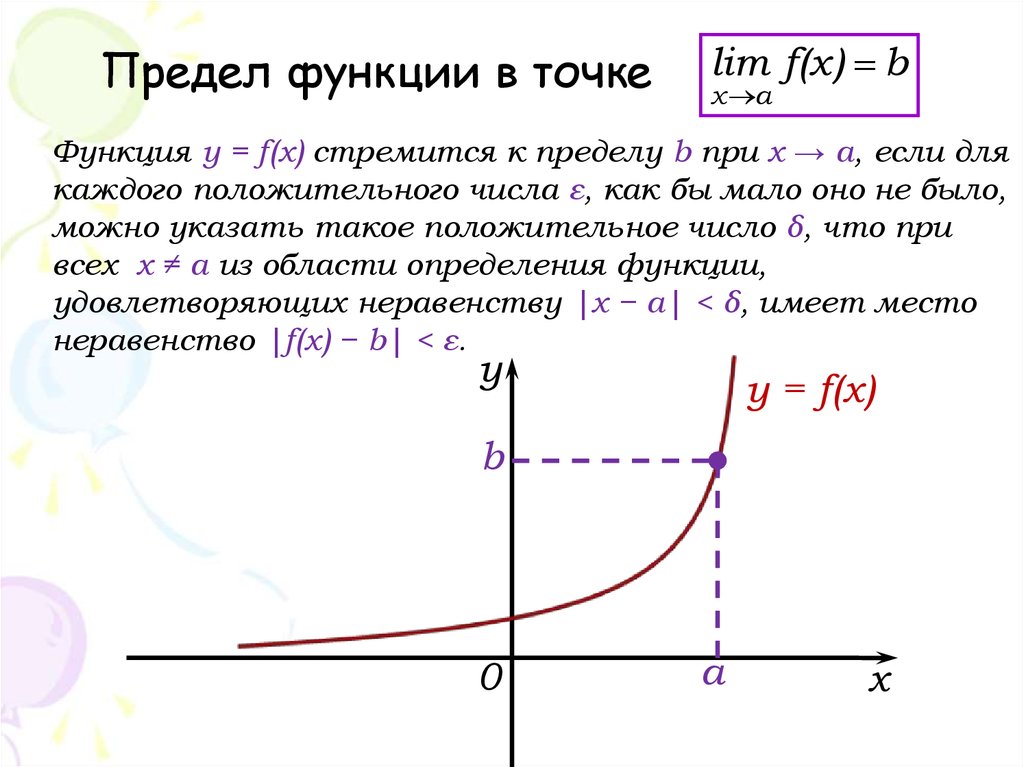
16. Предел функции в точке
lim f(x) bx a
Функция y = f(x) стремится к пределу b при x → a, если для
каждого положительного числа ε, как бы мало оно не было,
можно указать такое положительное число δ, что при
всех x ≠ a из области определения функции,
удовлетворяющих неравенству |x − a| < δ, имеет место
неравенство |f(x) − b| < ε.
у
y = f(x)
b
0
а
х
17.
18.
Функция (x) называется бесконечно малой величиной приx a (или при x ), если ее предел равен нулю:
lim ( x ) 0
x a
ПРИМЕР: Функция y x 3 является бесконечно малой при x 3.
В других точках эта функция бесконечно малой не является!
Теорема. Если функция f (x) при x a имеет предел, равный А, то ее
можно представить в виде суммы предела A и бесконечно малой (x)
при x a:
f ( x) A ( x)
Свойства бесконечно малых
Теорема 1. Сумма двух бесконечно малых есть бесконечно малая величина.
Теорема 2. Произведение бесконечно малой на ограниченную функцию (в
том числе на постоянную, на другую бесконечно малую функцию) есть
бесконечно малая.
19.
Функция f (x) называется бесконечно большой величиной приx a (или при x ), если для любого, даже сколь угодно
большого числа M > 0 найдется (зависящее от M), что для
всех x таких, что 0 < | x – a | < , выполнено неравенство:
| f (x) | > M.
lim f ( x)
x a
Связь между б.м. и б.б.
Теорема 1. Если (x) – бесконечно малая, то 1/ (x) бесконечно большая.
Теорема 2. Если (x) – бесконечно большая, то 1/ (x) бесконечно малая.
20. Таблица эквивалентности
Если предел отношения двух бесконечно малых равен единице:( x)
lim
1
x a ( x )
то их называют эквивалентными при x a (или при x ):
( x) ( x)
(1 ( x)) 1 ~ p ( x)
tg ( x) ~ ( x)
( x)
sin ( x ) ~ ( x )
a 1 ~ ( x) ln a
ln(1 ( x )) ~ ( x )
arcsin ( x ) ~ ( x )
2
1 cos ( x) ~ ( ( x)) / 2 arctg ( x) ~ ( x)
p
21.
22.
Рассмотрим теоремы, которые облегчают нахождение пределов функций.Формулировка теорем, когда x
будем пользоваться обозначением:
x0 или x аналогичны, поэтому
lim f ( x. )
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) limf1( x ) limf2 ( x )
Предел произведения двух функций равен произведению пределов:
lim f1( x ) f2 ( x ) lim f1( x ) limf2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C limf ( x )
23.
Предел дроби равен пределу числителя, деленному на пределзнаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же степени
предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )
24.
Если между соответствующими значениями трех функцийu u( x );
z z( x ); v v ( x )
выполняются неравенства:
u z v, при этом:
lim u( x ) lim v ( x ) A
тогда:
lim z( x ) A
Если функция f(x) монотонна и ограничена при x < x0 или при
x > x0, то существует соответственно ее левый предел:
lim f ( x ) A1
x x0 0
или ее правый предел:
lim f ( x ) A2
x x0 0
25. Вычисление пределов
Вычисление предела:lim f ( x ) A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
26. Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x)получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление пределов
в этом случае называется раскрытие неопределенности.
27. Первый замечательный предел
sin xlim
1
x 0
x
• Это означает, что синус малого угла есть
бесконечно малая того же порядка, что и
сам угол.
28. Второй замечательный предел
• Числом e (вторым замечательным пределом)называется предел числовой последовательности:
n
1
lim 1 e
n
n
• Это пример последовательности, которая монотонная и
ограничена.

























 mathematics
mathematics








