Предел последовательности

1. Предел последовательности

14.04.2020
Предел
последовательности
Ковалева Ирина
Константиновна

2.

• Что такое числовая последовательность?
• Какие бывают виды числовых
последовательностей?
• Как задаётся числовая последовательность?
• Что такое предел числовой
последовательности?
• Как находить предел числовой
последовательности?
Ковалева Ирина
Константиновна

3. Цели:

Узнать
Научиться
Ковалева Ирина
Константиновна

4. Найдите закономерности и покажите их с помощью стрелки:

1; 4; 7; 10; 13; …
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3
В порядке возрастания
положительные нечетные
числа
Чередовать увеличение
на 2 и увеличение в 2 раза
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
Ковалева Ирина
Константиновна
Увеличение в 2 раза
и уменьшение на 1

5. Что такое числовая последовательность?

•Если каждому натуральному числу п
поставлено в соответствие некоторое
действительное число хп , то говорят,
что задана числовая последовательность.
Числовая последовательность – это функция,
область определения которой есть множество N
всех натуральных чисел. Множество значений
этой функции – совокупность чисел хп , п ϵ Ν,
называют множеством значений
последовательности. Ковалева Ирина
Константиновна

6.

Способы задания
последовательности
Словесный
Аналитический
Рекуррентный
Рекуррентный (от лат. слова
recurrens – «возвращающийся»)
Ковалева Ирина
Константиновна

7. Словесный способ.

Правила задания последовательности
описываются словами, без указания формул или
когда закономерности между элементами
последовательности нет.
• Пример 1. Последовательность простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .
• Пример 2. Произвольный набор чисел: 1, 4, 12,
25, 26, 33, 39, ... .
• Пример 3. Последовательность чётных чисел
2, 4, 6, 8, 10, 12, 14, 16, ... .
Ковалева Ирина
Константиновна

8. Аналитический способ.

• с помощью формулы.
• Пример 1. Последовательность чётных чисел: y =
2n;
2, 4, 6, 8, …, 2п,… .
• Пример 2. Последовательность квадрата
натуральных чисел: y = n2;
1, 4, 9, 16, 25, ..., n2, ... .
• Пример 3. Последовательность y = 2n;
2, 22, 23, 24, ..., 2n, ... .
Ковалева Ирина
Константиновна

9. Рекуррентный способ.

• Указывается правило, позволяющее вычислить n-й
элемент последовательности, если известны её
предыдущие элементы.
• Пример 1. a1=a, an+1=an+d, где a и d – заданные
числа. Пусть a1=5, d=0,7, тогда последовательность
будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; ... .
• Пример 2. b1= b, bn+1= bn q, где b и q – заданные числа.
Пусть b1=23, q=½, тогда последовательность будет
иметь вид: 23; 11,5; 5,75; 2,875; ... .
Ковалева Ирина
Константиновна

10. Предел числовой последовательности

Рассмотрим две числовые последовательности:
( xn ) : 2, 4, 6, 8, 10, …,
( yn ) : 1,
,
,
,
1
2
,
2п
1
…
4
,…;
1
1
8, …16
1
2n
Изобразим члены этих последовательностей точками
на координатных прямых.
Обратите внимание как ведут себя члены
последовательности.
Ковалева Ирина
Константиновна

11. Замечаем, что члены последовательности уп как бы «сгущаются» около точки 0, а у последовательности хп таковой точки не

хn
yn
Замечаем, что члены последовательности уп как бы
«сгущаются» около точки 0, а у последовательности хп
таковой точки не наблюдается.
Но, естественно, не всегда удобно изображать члены
последовательности, чтобы узнать есть ли точка
«сгущения» или нет, поэтому математики придумали
следующее…
Ковалева Ирина
Константиновна

12.

Определение 1.
a - точка прямой, а r положительное
число. Интервал (a-r, a+r) называют
окрестностью точки a ,
а число r радиусом окрестности.
Пусть
Геометрически это выглядит так:
Ковалева Ирина
Константиновна

13. Например

(-0.1, 0.5) – окрестность точки 0.2, радиус
окрестности равен 0. 3.
Теперь можно перейти к определению точки
«сгущения», которую математики назвали
«пределом последовательности».
Ковалева Ирина
Константиновна

14.

Число b называется пределом последовательности
{уп } если в любой заранее выбранной
окрестности точки b содержатся все члены
последовательности, начиная с некоторого
номера.
Пишут:
Читают:
yn . b
y n стремится к
Либо пишут:
b.
lim yn b
.
n
Читают: предел последовательности уп при
стремлении п к бесконечности равен b.
Ковалева Ирина
Константиновна

15.

Последовательность, имеющая предел,
называется сходящейся; в противном
случае – расходящейся.
Ковалева Ирина
Константиновна

16. Рассмотрим последовательность:

1 1 1 1
1 – гармонический ряд
1; ; ; ; ; ...; ; ...
2 3 4 5
n
Если m N, k R, то
Если │q│< 1, то
lim
k
n n
m
1
lim 0
n n
0
lim q n 0
n
Если │q│> 1, то последовательность уn = q
расходится
Ковалева Ирина
Константиновна
n

17. Свойства пределов

Если
lim yn с
lim хn, b,
n
n
1. предел суммы равен сумме пределов:
lim хn уn b c
n
2. предел произведения равен произведению пределов:
lim хn уn bc
n
3. предел частного равен частному пределов:
хn
lim
n у n
b
с
4. постоянный множитель можно вынести за знак
предела:
lim kхn kb
n
Ковалева Ирина
Константиновна

18. Примеры:

1) lim
1
n n 2
1
1
1 1
lim lim lim 0 0 0
n n n
n n n n
2
5
2 5
2) lim 2 3 lim lim 2 lim 3 0 0 3 3
n n
n
n
n n n n
1
1
1
1 1
lim
...
lim
...
lim
0 ... 0 0
k
n n
n n n
n n n n n
3) lim
1
2n 2
3
2
2
2n 2 3
n
n
lim
4) lim 2
2
n n 4
n n 4
2
n2
n
3
lim 2 lim 2
n
n n
2 0
2
4 1 0
lim 1 lim 2
n
n n
3
2 2
lim
n
n
4
1
2
n
Ковалева Ирина
Константиновна
lim 2 3
2
n
n
4
lim 1 2
n
n

19.

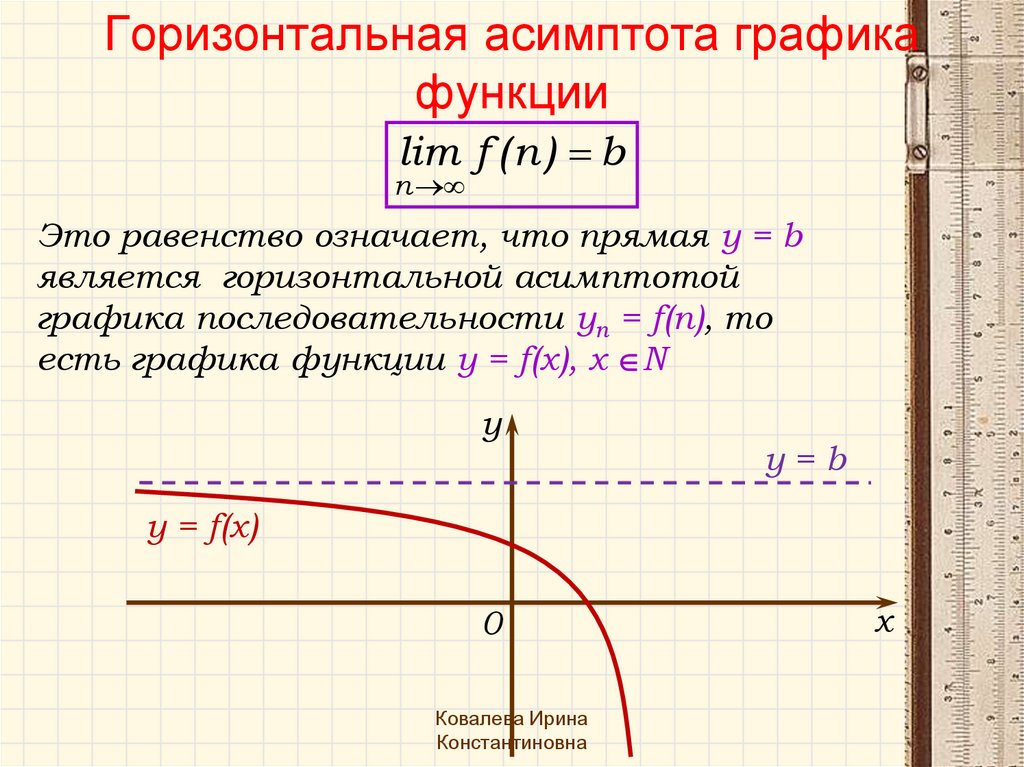
Горизонтальная асимптота графика
функции
lim f ( n ) b
n
Это равенство означает, что прямая у = b
является горизонтальной асимптотой
графика последовательности yn = f(n), то
есть графика функции y = f(х), х N
у
у=b
y = f(x)
0
Ковалева Ирина
Константиновна
х

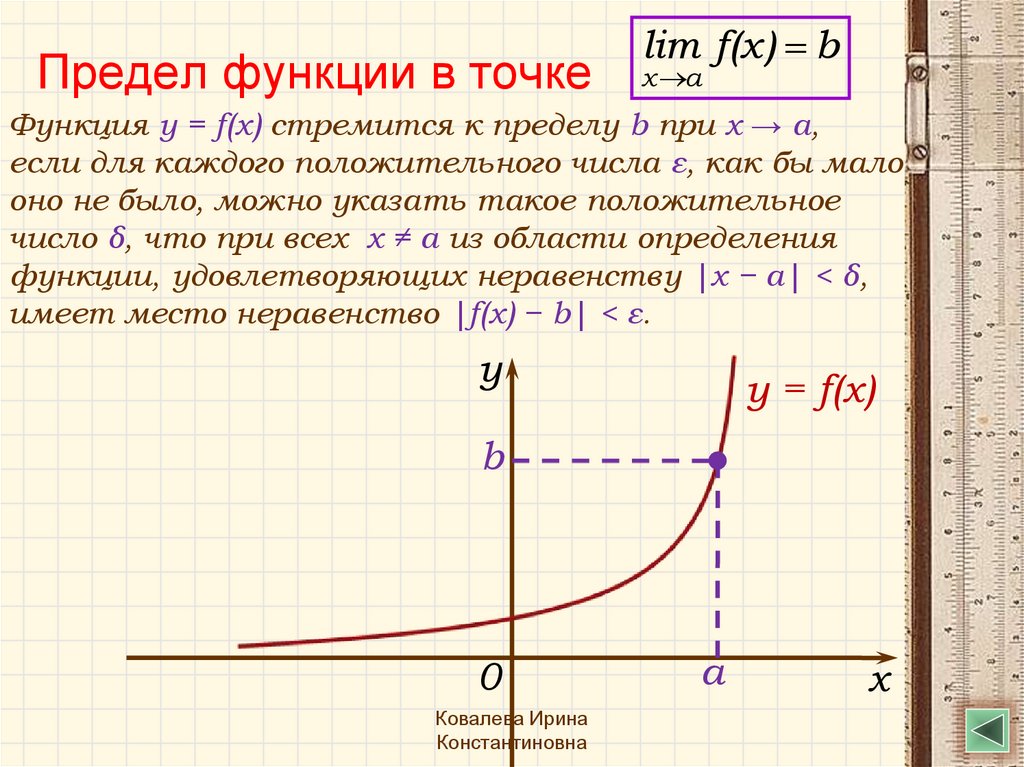
20. Предел функции в точке

lim f(x) b
x a
Функция y = f(x) стремится к пределу b при x → a,
если для каждого положительного числа ε, как бы мало
оно не было, можно указать такое положительное
число δ, что при всех x ≠ a из области определения
функции, удовлетворяющих неравенству |x − a| < δ,
имеет место неравенство |f(x) − b| < ε.
у
y = f(x)
b
0
Ковалева Ирина
Константиновна
а
х

21. Непрерывность функции в точке

Функцию y = f(x) называют непрерывной в точке
x = a, если выполняется условие
lim f(x) f ( a )
x a
Примеры:
1 lim x 3 2x 2 5x 3 13 2 12 5 1 3 7
x 1
2 lim
x 2
sin πx
x 4
sin 2π
2 4
0
2 4
0
x2 9 0
x 3 x 3
x 3
3 lim
lim
lim
x 3 4x 12
x 3 4
0 x 3 4 x 3
3 3
6
1,5
4
4
Ковалева Ирина
Константиновна

22. Понятие непрерывности функции

На рисунке изображен график
функции, состоящий из двух
«кусков». Каждый из них может
быть нарисован без отрыва от
бумаги. Однако эти «куски» не
соединены непрерывно в точке х =1.
Поэтому все значения х, кроме х =1, называют
точками непрерывности функции у = f(х), а
точку х =1 – точкой разрыва этой функции.
Ковалева Ирина
Константиновна

23. Стр. 62-63 Свойства функций непрерывных на отрезке

• № 14, 16
Ковалева Ирина
Константиновна

24.

Ковалева Ирина
Константиновна

25.

Ковалева Ирина
Константиновна

26.

Ковалева Ирина
Константиновна

27.

Ковалева Ирина
Константиновна