Сложение моментов импульса

1.

Сложение моментов импульса
Источники:
Конспект – раздел 3
Сакурай – §2.1, §5.2, приложение про атом водорода

2.

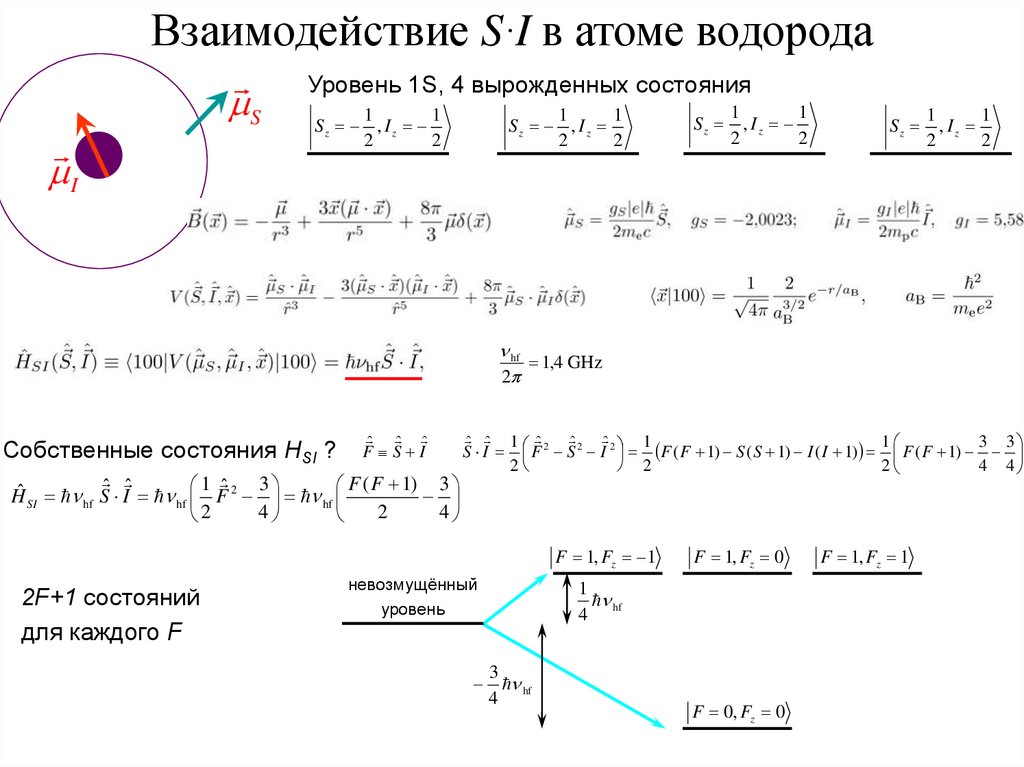
Взаимодействие S∙I в атоме водорода
S
I
Уровень 1S, 4 вырожденных состояния
1
1
Sz , I z
2
2
1
1
Sz , I z
2
2
1
1
Sz , I z
2
2
Sz
1
1
, Iz
2
2
hf
1,4 GHz
2
Собственные состояния HSI ?
ˆ ˆ ˆ
F S I
ˆ ˆ
3
1 ˆ
F ( F 1) 3
Hˆ SI hf S I hf F 2 hf
4
2
4
2
ˆ ˆ 1 ˆ
ˆ
ˆ
1
1
3 3
S I F 2 S 2 I 2 F ( F 1) S ( S 1) I ( I 1) F ( F 1)
2
2
2
4 4
F 1, Fz 1
2F+1 состояний
для каждого F
невозмущённый
уровень
3
hf
4
F 1, Fz 0
1
hf
4
F 0, Fz 0
F 1, Fz 1

3.

Коэффициенты Клебша-Гордана
F 1, Fz 1
1
1
Sz , I z
2
2
1
1
Sz , I z
2
2
1
1
Sz , I z
2
2
1
1
Sz , I z
2
2
F 1, Fz 0
1
hf
4
3
hf
4
F , Fz
1/ 2
F 0, Fz 0
1/ 2
S ,I
S z 1 / 2 I z 1 / 2
z
z
S z , I z F , Fz
1
1
Fˆ F 1, Fz 1 Sˆ Iˆ S z , I z
2
2
1
1
1
1
1
1
F 1, Fz 1 S , S z
I , Iz
Sz , I z
2
2
2
2
2
2
Jˆ j, jz ( j jz )( j jz 1) j, jz 1
F 1, Fz 0
F 1, Fz 1
1
1
1
1
1
1
Sz , I z
Sz , I z
2
2
2
2
2
2
1
1
1
1
F 0, Fz 0 a S z , I z b S z , I z
2
2
2
2
F 0, Fz 0 F 1, Fz 0 0
F 1, Fz 0
поскольку
Fˆ , Sˆ 0, Fˆ , Iˆ 0
z
z
z
z
1
1
1
1
1
1
Sz , I z
Sz , I z
2
2
2
2
2
2

4.

Эффекты Зеемана
Источники:
Сакурай – §5.1, §5.3

5.

E
Спин электрона в постоянном магнитном поле B.
Hˆ ˆ B ˆ z B L Sˆ z ,
L
|e| B
me c
E L
B = 0 – базис любой, ΔE = 0
B > 0 – базис только { |+>, |-> }, ΔE > 0
Эффекты Зеемана для 1s-орбитали водорода
ˆ ˆ
ˆ
H hf S I ˆ B
ˆ ˆ
ˆ
H hf S I L Sˆ z
Hˆ , F ˆ 2 0,
Hˆ , Fˆ 0
z
g | e | B ˆ
ˆ B L Sˆ z I
I z L Sˆ z
mp c
– собственные состояния и значения?

6.

B≈0
B=0
F 1, Fz 1
F 1, Fz 0
F 1, Fz 1
F 1, Fz 1
F 1, Fz 0
F 1, Fz 1
ΔE
-ΔE
hf
F 0, Fz 0
F 0, Fz 0
L
E F 1, Fz 1 Hˆ F 1, Fz 1 L Sˆ z
2
любое B: решение диагонализацией
матрицы 4x4 S z ' ' , I z ' ' Hˆ S z ' , I z '
B→∞
ˆ ˆ
ˆ
H hf S I L Sˆ z L Sˆ z
S z , I z ,
S z , I z :
S z , I z ,
S z , I z :
L
E
2
E L
2
4 S z , I z
3 S z , I z
3 F 1, Fz 0
1 F 0, Fz 0
2 S z , I z
1 S z , I z

7.

тонкое расщепление
Источник:
Сакурай – §3.6, §3.10 в издании 1994 г. (§3.11 в 3-м издании), §5.3

8.

Взаимодействие L∙S в атоме
1
1 x dV
e
1
E V ( r )
S
Beff v E ~ p x
e
e r dr
me c
c
ˆ 2
ˆ ˆ
p
1 1 dV ˆ ˆ
ˆ
ˆ
ˆ
H
V ( rˆ) H LS
H LS Beff 2 2
L S
2me
me c rˆ drˆ
ˆ ˆ
Hˆ LS f L S
2
1 1 dV
e2 1 e2
4,4 10 6 Ry
f 2 p 2 2
2p
me c rˆ drˆ
2aB 12 c
ˆ ˆ ˆ
J L S
ˆ
ˆ
ˆ ˆ ˆ
J 2 L2 2 L S S 2
H LS ~ j ( j 1) l (l 1)
3
4
jz
Уровень 2P, 6 состояний:
lz 1, sz
1
2
lz 0, sz
1
2
3
2
jz
1
2
jz
1
2
jz
1
2
jz
1
2
j = 3/2
lz 1, sz
1
2
j = 1/2
jz
3
2

9.

Домашнее задание
1/3 от суммарной оценки за все дз
Сдавайте до 21:00 среды 28 февраля Илье Юхновцу [email protected] не более 1 Мб
1. (40 баллов) Найдите собственные состояния оператора энергии сверхтонкого
взаимодействия и соответствующие энергетические сдвиги для S=1/2, I=1 (таков
спин ядра в 6Li). Считайте νhf известной.
2. (20 баллов )
Hˆ , F ˆ 2 ?
Hˆ , Fˆ ?
z
ˆ ˆ
Hˆ hf S I L Sˆz
Сдавайте до 21:00 вторника 5 марта Илье Юхновцу [email protected] не более 1 Мб
ˆ ˆ
3. (50 баллов) Найдите собственные состояния гамильтониана Hˆ hf S I L Sˆ z
для произвольного B. Рассматривайте атом водорода, то есть νhf = 1,4 ГГц.
Количественно охарактеризуйте условия B ≈ 0 и B → ∞. Удостоверьтесь в
асимптотически верном поведении энергий и состояний.