Similar presentations:
Спин, матрицы Паули
1.
Спин электрона. Матрицы ПаулиИз эффекта Зеемана следует, что если есть спин, то он создаёт магнитный момент. Поэтому
постулируем, что коммутационные соотношения для оператора спина такие же, как и у
орбитального момента импульса. Для краткости оператор спина будем считать безразмерным
sˆi , sˆk ieikl sˆl
eikl
sˆ 2 , sˆk 0, sˆ 2 sˆx2 sˆy2 sˆz2
абсолютный антисимметричный тензор третьего ранга
Представление
ssz
Собственные значения
3
1
sˆ 2 s(s 1) , sˆz sz
4
2
Кет-векторы и волновые функции
,
2
a, b, a , b
2
a
sz
b
- амплитуды вероятности и вероятности обнаружить электрон в состоянии с
проекцией спина на ось Oz равной 1/ 2
1
2.
«Лирическое отступление.Расшифровка фразы «двузначность, не описывающаяся КЛАССИЧЕСКИ»
Состояние частицы с орбитальным моментом l=1
l 1, m
ll z
- представление
1
0
0
llz l 1, m 1 0 , llz l 1, m 0 1 , llz l 1, m 1 0
0
0
1
Координатное представление
l 1, m 1 Y11 ( , ), l 1, m 0 Y10 ( , ), l 1, m 1 Y1 1( , )
Классический момент импульса
ˆ
ˆ
M l
0,l
M r p
3.
Спиновый кет-вектор частицыs ,
2
Существует только
ssz- представление
1
0
ssz s , sz
, ssz s , sz
2
2
2
2
0
1
Классический предел
sˆ
0
0
4.
Операторы спинаИз теории момента
jjz ˆjz jjz jz jz jz ,
jjz ˆj 2 jjz j ( j 1) jz jz
jjz ˆj jjz 1 jjz 1 ˆj jjz ( j jz )( j jz 1)
В рассматриваемых условиях
1
j s ,
2
jz sz
Найти операторы спина?
1
2
5.
Правило нумерации строк и столбцовs z 1/ 2
s z 1/ 2
sz 1/ 2
sz 1/ 2
f11 f12
f
f
21 22
Найти операторы спина?
6.
Результат1 1 0
sz sˆz s z
2 0 1
0 0
sz sˆ s z
,
1 0
3 1 0
2
ˆ
sz s s z
4 0 1
0 1
sz sˆ s z
0
0
Матрицы x,y - проекции спина?
7.
Матрицы Паулиˆs 1 ˆ
2
ˆ x (1)
0 1
0 i
1 0
, ˆ y (2)
, ˆ z (3)
1 0
i 0
0 1
Матрицы вместе с единичной матрицей
1 0
ˆ 0
0 1
образуют полный базис в пространстве двухрядных матриц!
8.
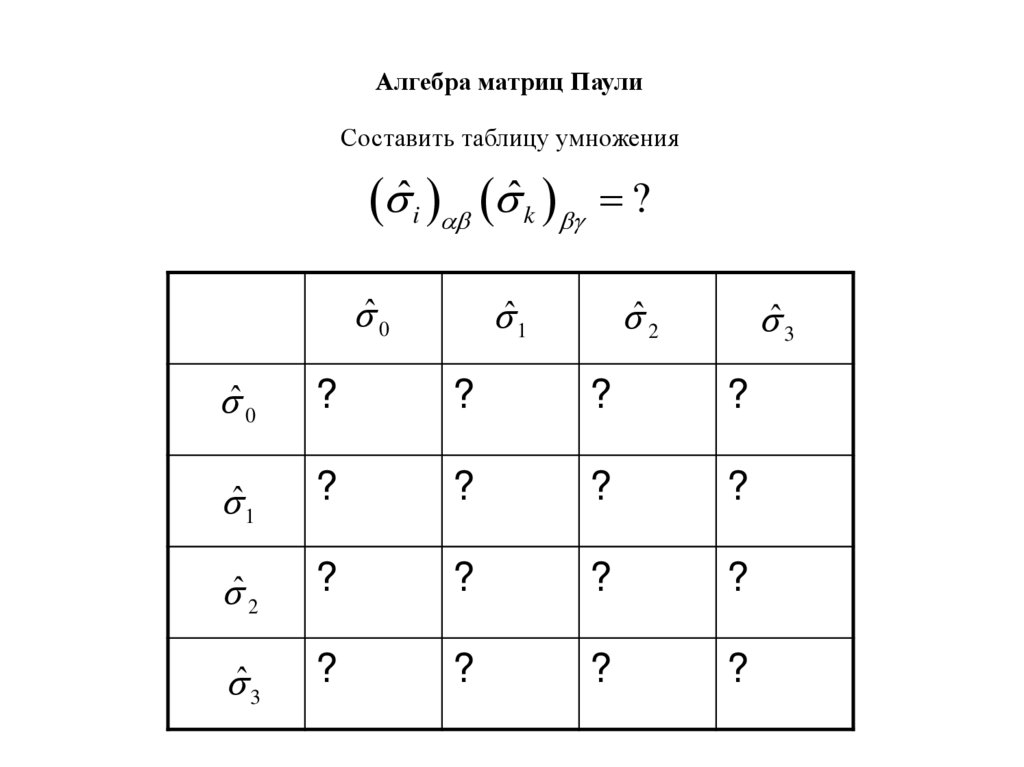
Алгебра матриц ПаулиСоставить таблицу умножения
ˆi ˆ k
ˆ 0
?
ˆ1
ˆ 2
ˆ 3
ˆ 0
?
?
?
?
ˆ1
?
?
?
?
ˆ 2
?
?
?
?
ˆ 3
?
?
?
?
9.
Таблица умноженияˆ 0
ˆ1
ˆ 2
ˆ 3
ˆ 0
ˆ 0
ˆ1
ˆ 2
ˆ 3
ˆ1
ˆ1
ˆ 0
i ˆ 3
i ˆ 2
ˆ 2
ˆ 2
i ˆ 3
ˆ 0
i ˆ1
ˆ 3
ˆ 3
i ˆ 2
i ˆ1
ˆ 0
Используя абсолютный антисимметричный тензор и символ Кронекера,
записать в «ковариантном» виде
ˆi ˆ k
ˆ ?
10.
РезультатВнимание:
«немое» суммирование проводится только по дважды повторяющимся греческим индексам
3
ˆ i ˆ k ik ˆ 0 i eikl ˆ l ,
i, k 1,2,3
l 1
Греческие индексы обычно принято не указывать, т.е.
3
ˆ i ˆ k ik ˆ 0 i eikl ˆ l , i, k 1,2,3
l 1
11.
ЗАДАЧИ(i,k=1,2,3)
ˆ i ˆ k ˆ k ˆ i ?
Sp ˆ i ˆ k ?
?
ˆ a ˆb ?
ˆ a
2
?
Sp ˆ ˆ a ˆ b
12.
Пример решенияˆ a ˆb a b ˆ
i k
ˆ k
i
ˆ a ˆ b ab ˆ
3
ˆ
ˆ
aibk ik 0 i eikl l
l 1
3
0
i eikl aibk ˆ l ab ˆ 0 i a b ˆ
l 1
a b ey ey2 1
13.
ОТВЕТЫ14.
ЗАДАЧИНайти явный вид операторов
?,
exp i ˆ y ?, exp i n ˆ
?
exp n ˆ
Указание: воспользоваться формулой Эйлера и
представить косинус и синус в виде ряда Тейлора.
15.
ОТВЕТЫIˆ ˆ 0













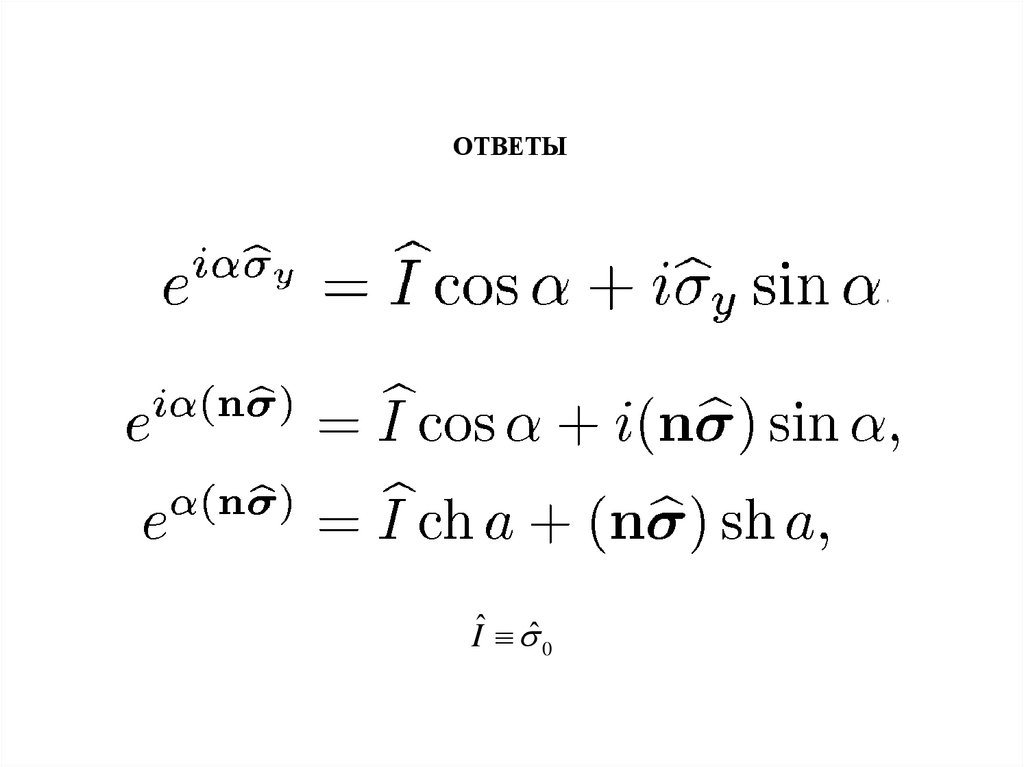
 physics
physics








