Similar presentations:
Матричная теория момента в обозначениях Дирака
1.
МАТРИЧНАЯ ТЕОРИЯ МОМЕНТА В ОБОЗНАЧЕНИЯХ ДИРАКАИсходные формулы – коммутационные соотношения
ˆji , ˆjk ieikl ˆjl
ˆj 2 , ˆj 0,
k
eikl
ˆj 2 ˆj 2 ˆj 2 ˆj 2
x
y
z
абсолютный антисимметричный тензор третьего ранга
Частный случай – пространственный момент импульса
ˆj lˆ rˆ pˆ
В дальнейшем величину
ˆj
будем называть спиновым моментом или, кратко, моментом.
Одновременно измеримы квадрат момента и одна из проекций. Согласно общепринятым
правилам, выберем в качестве «спиновых» квантовых чисел, характеризующих состояние
системы выберем следующие
ˆjz Jjz jz Jjz
ˆj 2 Jj J 2 Jj
z
z
2.
Вводим операторыˆj ˆjx i ˆj y , ˆj 2 , ˆj 0,
C jz jz , jz jz 1
Jjz ˆj Jjz
j z jz 1
0,
Матричный элемент коммутатора
J j z ˆj 2 , ˆj Jjz J jz ˆj 2 ˆj Jjz J jz ˆj ˆj 2 Jj z
ˆj 2 J j J j ˆj Jj
ˆj 2 Jj
ˆ
J
j
J
j
j
J
j
J
j
z
z z z
z
z
z
z
J jz
J jz
2
2
ˆ
J
J
j
J
j
J
j
j
Jj
J
J j z ˆj J j z J j z Jjz
z
z
z
z
J jz
J jz z
J 2 J j z ˆj Jjz J 2 J j z ˆj Jjz J 2 J 2 J j z ˆj Jj z 0
Отличны от нуля только матричные элементы с одинаковым квадратом момента
J j z ˆj Jjz Jj z ˆj Jjz JJ
3.
Матричные элементы x,y -проекций момента1
J j z ˆjx Jjz Jj z ˆj Jjz Jj z ˆj Jjz JJ
2
i
J j z ˆj y Jjz Jj z ˆj Jjz Jj z ˆj Jjz JJ
2
Матричные элементы проекций момента и их линейных комбинаций отличны от нуля только
при одинаковых значениях квадрата момента J!
4.
Ограниченность значений z-проекции моментаJjz ˆj 2 ˆjz2 Jjz J 2 jz2 Jjz ˆjx2 ˆj y2 Jjz
jz
Jjz ˆjx Jjz Jjz ˆjx Jjz Jjz ˆj y Jjz Jjz ˆj y Jj z
j Jjz ˆjx Jjz
z
jz
2
Jjz ˆj y Jjz
2
0
Таким образом
jmin jz jmax
5.
Коммутаторˆj , ˆjz ˆjx , ˆjz i ˆj y , ˆjz iexzy ˆj y i ieyzx ˆjx i ˆj y
ˆjx
Или
ˆj , ˆjz ˆj
Коммутатор
ˆj , ˆj ˆjx i ˆj y , ˆjx i ˆj y i ˆj y , ˆjx ˆjx , ˆj y
i ieyxz ˆjz iexyz ˆjz 2 ˆjz
Или
ˆj , ˆj 2 ˆjz
ˆj
x
i ˆj y
6.
Выберем состояние с заданной z-проекциейˆjz Jjz jz Jjz
Построим из него новое состояние
ˆj Jjz
Подействуем на него оператором z- проекции
ˆjz ˆj Jjz
ˆj ˆj
z
ˆj Jjz jz 1 ˆj Jjz
Таким образом
ˆj Jjz Jj Jjz 1
z
7.
Из ограниченности z-проекции момента следуетˆj Jjmax 0,
ˆj Jjmin 0
Но
ˆj 2 ˆj 2 ˆj 2 ˆj 2 1 ˆj ˆj
x
y
z
4
2
1 ˆ ˆ
j j
4
2
Или
ˆj 2 ˆj ˆj ˆj 2 ˆj ˆj ˆj ˆj 2 ˆj
z
z
z
z
Поэтому
ˆj 2 Jj
2
J
Jjmax ˆj ˆj
max
ˆj 2 Jj
2
Jjmin ˆj ˆj
min J
ˆj Jj
ˆjz2 ˆjz Jjmax jmax jmax 1 Jjmax
ˆjz2
z
min
1 ˆ ˆ ˆ ˆ
2
ˆ
jz j j j j ˆjz2
2
jmin jmin 1 Jjmin
8.
Или2
2
jmax
jmax jmin
jmin 0
jmax jmin jmax jmin 1 0
Обращаем в нуль второй сомножитель
jmax jmin 1 0
jmax jmin 1 jmin !
Поэтому выбираем
jmax jmin j
Таким образом для собственных значений квадрата момента находим
J 2 j j 1
ВАЖНЕЙШЕЕ СЛЕДСТВИЕ
1 3
j 0, ,1, ,
2 2
9.
Матричные элементы «повышающего» и «понижающего» операторовРассмотрим диагональный элемент
jjz ˆj ˆj jjz jjz ˆj jjz
jz
jjz ˆj jjz
jjz ˆj jjz 1 jjz 1 ˆj jjz jjz ˆj jjz 1
2
С другой стороны
jjz ˆj ˆj jjz jjz ˆj 2 ˆjz2 ˆjz jjz j ( j 1) jz2 jz
( j jz )( j jz 1)
Используя неопределённость фазы волновой функции, находим
jjz ˆj jjz 1 jjz 1 ˆj jjz ( j jz )( j jz 1)
Контрольный вопрос. Чему равно?
ˆj jjz 1 ?
ˆj jjz ?
10.
Вспомогательные формулыˆj jjz jj jjz 1
z
jjz ˆj jjz 1 jjz 1 jjz jjz
Ответ
ˆj jjz 1 ( j jz )( j jz 1) jjz
ˆj jjz ( j jz )( j jz 1) jjz 1






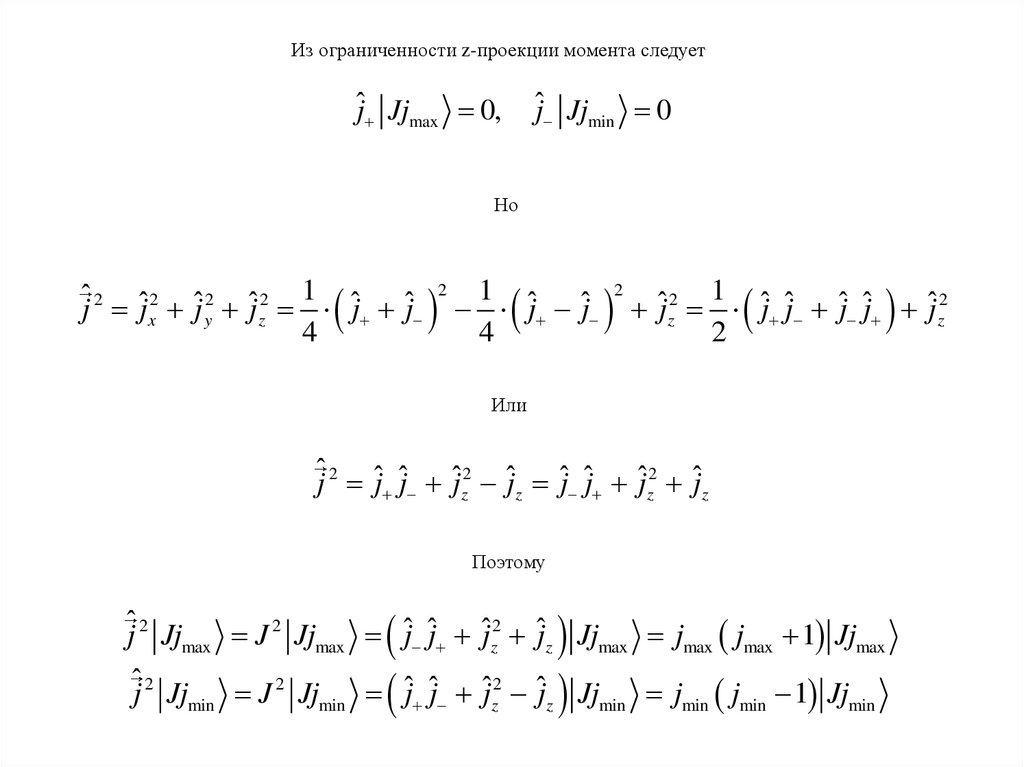



 mathematics
mathematics physics
physics








