Обозначения Дирака
1.
ОБОЗНАЧЕНИЯ ДИРАКАКраткий математический обзор формального аппарата квантовой механики см.
Елютин, Кривченков, Квантовая механика
Ключевое понятие квантовой механики – понятие состояния системы.
Примеры.
1. Квантовый осциллятор находится в n-ом состоянии, т.е. квантовая частица находится в гармоническом
потенциале, обладает энергией En n 1/ 2 . Известны собственные волновые функции в
координатном, импульсном и энергетическом представлениях.
4
2
2. Атом водорода в s-состоянии, т.е. электрон находится в поле протона, обладает энергией En 1l 0 m 0 mee /(2 )
, квадрат момента и проекция момента импульса равны нулю.
Известны собственные волновые функции в координатном, импульсном и энергетическом представлениях.
Для краткого обозначения состояния системы Дирак предложил использовать значок (кет-вектор)
С математической точки зрения кет-вектор является вектором в абстрактном векторном пространстве. Как и
со всяким обычным вектором, его можно складывать с другим кет-вектором, а также умножать на
комплексные числа. Можно также определить правило соответствия между двумя множествами кетвекторов, т.е. задать оператор, действующий на кет-векторы.
C (C C1 iC2 )
C C
кет-вектор, описывающий то же состояние системы, что и кет-вектор
кет-вектор, описывающий состояние системы, получающееся с помощью
суперпозиции состояний и
2.
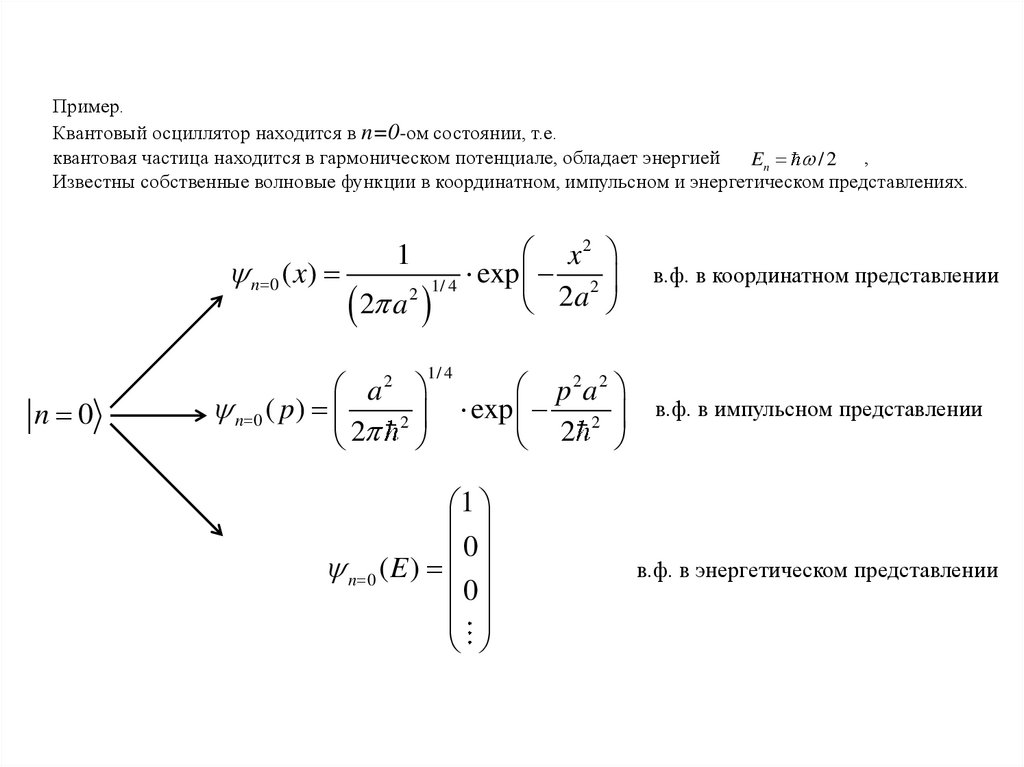
Пример.Квантовый осциллятор находится в n=0-ом состоянии, т.е.
квантовая частица находится в гармоническом потенциале, обладает энергией
En / 2 ,
Известны собственные волновые функции в координатном, импульсном и энергетическом представлениях.
n 0 ( x )
n 0
1
2 a
a
n 0 ( p )
2
2 1/ 4
2
1/ 4
2
x2
exp 2
2a
в.ф. в координатном представлении
p 2a 2
exp
2
2
в.ф. в импульсном представлении
1
0
n 0 ( E )
0
в.ф. в энергетическом представлении
3.
Как и для обычного вектора, для кет-векторов можно определить скалярное произведение. Дляэтого Дирак ввёл так называемый бра-вектор
†
Обозначение скалярного произведения
Расшифровка скалярного произведения на примере осциллятора в координатном представлении
mn
dx
m ( x) n ( x) mn
Расшифровка скалярного произведения на примере осциллятора в энергетическом представлении
m 0 n 1 1 0 0
0
1
0
0
4.
Физическая интерпретация скалярного произведенияВ случае «школьных» векторов скалярное произведение
a b a cos b
при b=1 равно проекции вектора
a на направление вектора b
Какая ситуация в случае Дираковских кет- и бра-векторов?
x кет-вектор состояния осциллятора, в котором он обладает определённой координатой
n
кет-вектор состояния осциллятора, в котором он обладает определённой энергией
Проекция кет-вектора
n
на кет-вектор
x
- скалярное произведение
xn
имеет смысл амплитуды вероятности того, что осциллятор с энергией
x n n ( x)
E nбудет обнаружен в окрестности точки x
5.
Принцип суперпозиции в обозначениях ДиракаРассмотрим произвольное состояние квантового осциллятора
Разложим кет-вектор этого состояния по собственным состояниям квантового осциллятора
an n
n
Домножим на бра-вектор
m
m an m n an mn am
n
n
Ещё одна форма записи принципа суперпозиции
n n n n
n
n
Единичный оператор
n
n
n 1̂
6.
Операторы в обозначениях ДиракаОператор - правило соответствия между двумя множествами кет-векторов
fˆ ,
k k ,
l l
k
l
В явном виде это равенство формально совпадает с действием матрицы на столбец. Покажем это на примере
квантового осциллятора.
l
l fˆ k k
l
nl
l
k
l n fˆ k k ,
n l nl
k
n n fˆ k k
k
n , k
волновые функции состояний и осциллятора в энергетическом представлении
0
0
n 1 , k 1 ,
0 f11 f12 f13
1 f 21 f 22 f 23
0
1
7.
Матричные элементы оператора в координатном представленияхn fˆ k
dx
( x) fˆ k ( x)
n
Матричные элементы оператора в энергетическом представлениях
n fˆ k 0
an 1 0
f11 f12 f13
f 21 f 22 f 23
0
ak 1 f kn
0
8.
Матричный элемент произведения операторовn fˆ gˆ k n fˆ i i gˆ k n fˆ i i gˆ k
i
i
Матрица произведения операторов в энергетическом представлениях
f11 f12 f13
n fˆ gˆ k f 21 f 22 f 23
g11 g12 g13
g 21 g 22 g 23
9.
Операторы в обозначениях Дирака.Непрерывный спектр (координатное представление)
Единичный оператор
dx
x x 1
Действие оператора
x dx x fˆ x x
x , x
волновые функции состояний
представлении
F ( x, x ) x fˆ x
и
осциллятора в координатном
ядро оператора fˆ в координатном представлении
x dx x fˆ x x ( x) dx F ( x, x ) ( x )
10.
Матричный элемент произведения операторов. Непрерывный спектрn fˆ gˆ k n fˆ
dx x x gˆ k dx n fˆ x
x gˆ k
Ядро произведения операторов в координатном представлении
x fˆ gˆ x
ˆ x x gˆ x dx F x, x G x , x
dx
x
f








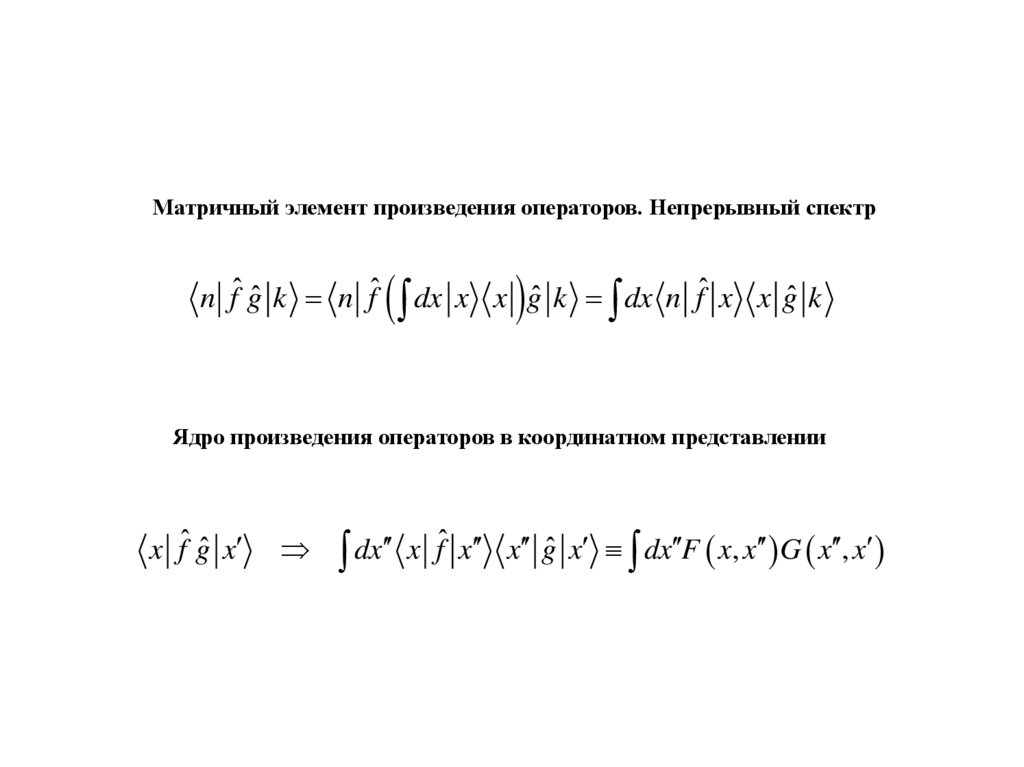
 physics
physics