Similar presentations:
Интегрирование биномиальных дифференциалов
1.
Интегралы вида x m a bx ndx .
p
Интегрирование биномиальных дифференциалов
Учебное пособие:
Кл: В157.
теория - с. 31, примеры 1.23-1.25.
dx
x 1 x
3
. В154.
3
1 4 x
dx .
x
В156.
dx
x3 1 4 x3
.
3
Д/з: B 155, 158
В 232
x
В 245
dx
В 236
3
dx
x 4
2
2
x x 1
2
dx
x x
2
3/2
(биномиальный дифференциал и
dx
x
k
ax dx c
2
)
(биномиальный дифференциал и дробно-линейная подстановка)
(биномиальные дифференциалы и подстановка Абеля)
1
2.
Интегралы вида x a bx dx .n
m
В157.
dx
x 1 x
3
p
p 1 ,
1
1
m ,n ,
3
2
x t НОК ( 2,3) t 6
1
6
2
t
1
2
t
5
dt
dt 6
t
6
t
1
2
1 t
1
6 3
6 t arctg t C 6 6 x arctg 6 x C
2
3.
Интегралы вида xВ154.
3
m
a bx dx .
n
p
1 4 x
dx
x
1
p ,
3
1
1 m 1
m , n ,
2
2
4
n
4
3
3
4
1 x t , x t 1
t 1
3
1
4
2
1
3 3
t 4 t 1 3t dt 12 t 1
12 t 3 1 t 3 dt
3
3
2
3
2 3 1 2
t
dt
12 7
t 3t 4 C , t 3 1 4 x .
7
3
4.
Интегралы вида x a bx dx .m
В156.
dx
x3 3 1 4 x3
n
p
1
p ,
3
3
3 m 1
2
m 1
m ,n ,
,
p 1 ,
2
4
n
3
n
4
4
3
1
t
4 3
x 3 1 t 3 , x t 3 1 3 ,
1
x
1
t 3 1 t 3 1
t 3 1
4 3
3 2
4 t 3 1
1 7
2
3 3
1
3
7
t 4 3
3 3t 2 dt
t
1
3
t 1 3
3
t 1 2 dt 4 tdt 2t 2 C , t 3
1
1.
3/ 4
x
4
5.
22
2
2
Интегралы вида R x , a x dx , R x , x a dx .
Тригонометрические и гиперболические подстановки
Учебное пособие:
Кл: В 149.
В 151.
теория - с. 52,
примеры 1.30-1.41.
x2
a x
2 3/2
2
dx
,
2 3/2
x a
2
dx , x a sin t .
x a tg t , x a sh t .
Д/з: B 146-148, 150
5
6.
В149.x a sin t ,
a 2 sin 2 t
sin 2 t
a 2 x2 3/2 dx a 2 x2 a 2 cos2 t a3 cos3 t a cos t dt cos2 t dt
x2
1 cos 2 t
dt tg t t C
2
cos t
sin t
1 sin 2 t
t C
x/a
x
x
x
arcsin C
arcsin C .
a
a
1 x2 / a2
a2 x2
6
7.
В151. Способ 1. Тригонометрическая подстановка x a tg t .x a tg t ,
3
dx
cos
t a dt
1
2
x 2 a 2 3/2 x 2 a 2 a a3 cos2 t a 2 cos tdt
cos 2 t
1
1
tg t
1
x/a
x
sin
t
C
C
C
C.
2
2
2
2
2
2
2
2
2
a
a 1 tg t
a 1 x / a
a a x
В151. Способ 2. Гиперболическая подстановка x a sh t .
x a sh t ,
1
1
dt
x2 a2 3/2 x2 a2 a ch t a3 ch3 t a ch t dt a2 ch 2 t
dx
1
1
sh t
1
x/a
x
th
t
C
С
C
C .
2
2
2
2
2
2
2
2
2
a
a 1 sh t
a 1 x / a
a a x
7
8.
В151. Способ 3. Подстановка Абеля.dx
x a
2
2
3/ 2
1
dx
.
2
2
2
2
x a x a
Подстановка Абеля t
x a
2
2
x
x
x a
2
2
.
t x2 a2 x .
t x a x x a a ,
2
2
2
2
2
a2
x a 1 t2 .
2
2
2
2
dt x a t
2
2
x a dx dx
2
2
,
x
dt x 2 a 2 t t dx dx
dt
dx
1 t2
x2 a2
1 t 2 dt
t
x
C
C
x2 a2 3/2 a2 1 t 2 a2
2
2
2
a x a
dx
8
9.
Интегралы вида R( x, ax 2 + bx + c ) dx .Подстановки Эйлера.
Учебное пособие:
теория - с. 35,
примеры 1.26-1.28.
Дз:
В239.
dx
x x x 2
Д1969.
2
(1, 3 подстановки Эйлера и
x x 2 3x 2
x x 3x 2
2
dx
x
k
ax dx c
2
dx (3 подстановка Эйлера)
9
)





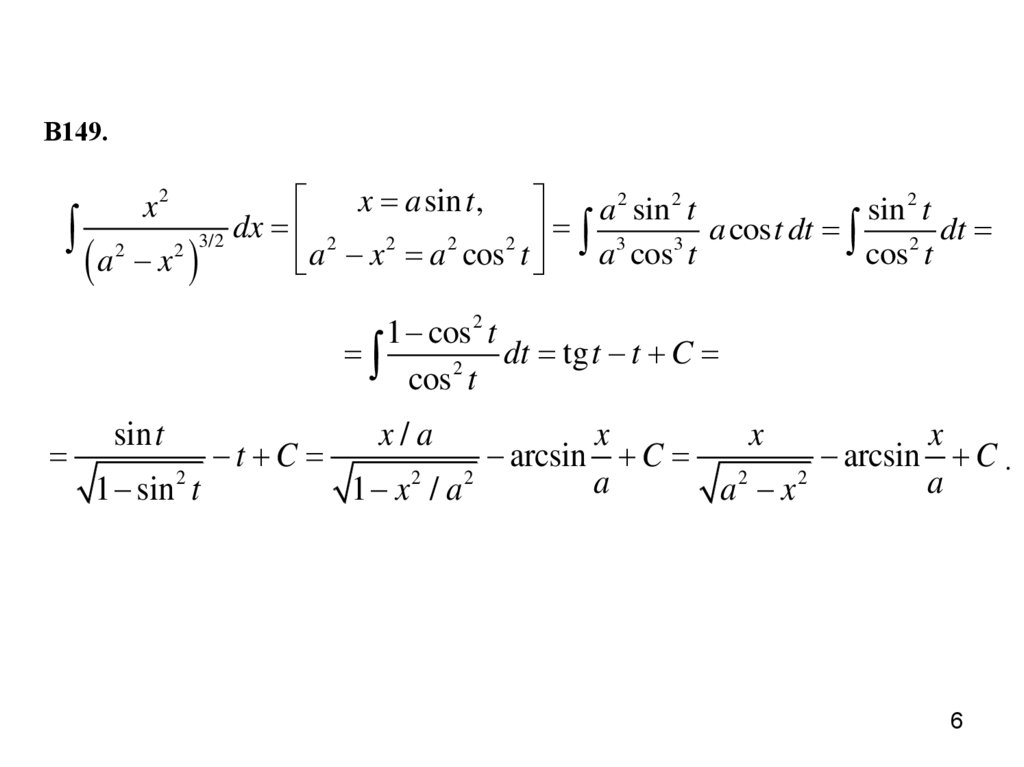



 mathematics
mathematics








