Анализ переходного процесса. Принужденный и переходные режимы

1.

Анализ переходного процесса.
Принужденный и переходные
режимы.
Омск 2024
Жавнер А.А.
Буданцев С.С.

2.

Анализ переходных процессов
Как известно, напряжения и токи в индуктивностях и емкостях являются
производными и интегралами соответствующих величин. Поэтому уравнения
Кирхгофа для электрической цепи содержащей реактивные элементы будут
дифференциальными или интегро-дифференциальными и задачей анализа
переходных процессов является их решение.
Для несложных электрических цепей с постоянными параметрами систему
уравнений Кирхгофа методом подстановки можно свести к одному
дифференциальному уравнению с постоянными коэффициентами, порядок
которого будет равен числу реактивных элементом цепи. Если в схеме цепи
после коммутации отсутствуют источники электрической энергии, то
уравнение будет однородным, т.е. его правая часть будет равна нулю, в
противном случае уравнение будет неоднородным.

3.

Свободную составляющую решения ищут в виде функции a=Aept . Эта функция зам
Частное решение неоднородного дифференциального уравнения обычно проще на

4.

В зависимости от вида корней характеристического уравнения, который
зависит только от соотношения между R, L и C, в данной цепи различают три
разных по характеру ПП: апериодический; предельный случай апериодического
и периодический. Апериодический заряд конденсатора при включении цепи R,
L, C на постоянное напряжение
Апериодическим называется заряд емкости, при котором напряжение на С
монотонно увеличиваясь достигает своего установившегося значения, т.е. не
происходит перезарядки конденсатора. Такой характер ПП имеет место, если р1 и
р2 являются вещественными и разными. Как следует из (2) это будет, когда
подкоренное выражение положительно, т.е.
Rкр называется критическим сопротивлением данной цепи – это такое наименьшее сопротивление, при кот

5.

Кривая uC начинается с нуля, но так, что , поскольку i(0)=0. Затем она
монотонно возрастает до uCпр=U . Кривая тока начинается с нуля и
возрастает до максимального значения при t1, в который кривая uC
испытывает перегиб, а затем убывает до нуля. Напряжение uL изменяется от
U (uL (0+)=U) до нуля при t1, затем становится отрицательным и при t2, когда
пергибается кривая тока, имеет минимум. Моменты времени t1 и t2 можно
рассчитать так: Изменение знака uL может быть объяснено так: когда ток
возрастает ЭДС самоиндукции противодействует его возрастанию и uL>0, а
когда ток уменьшается ЭДС самоиндукции поддерживает его и uL<0.

6.

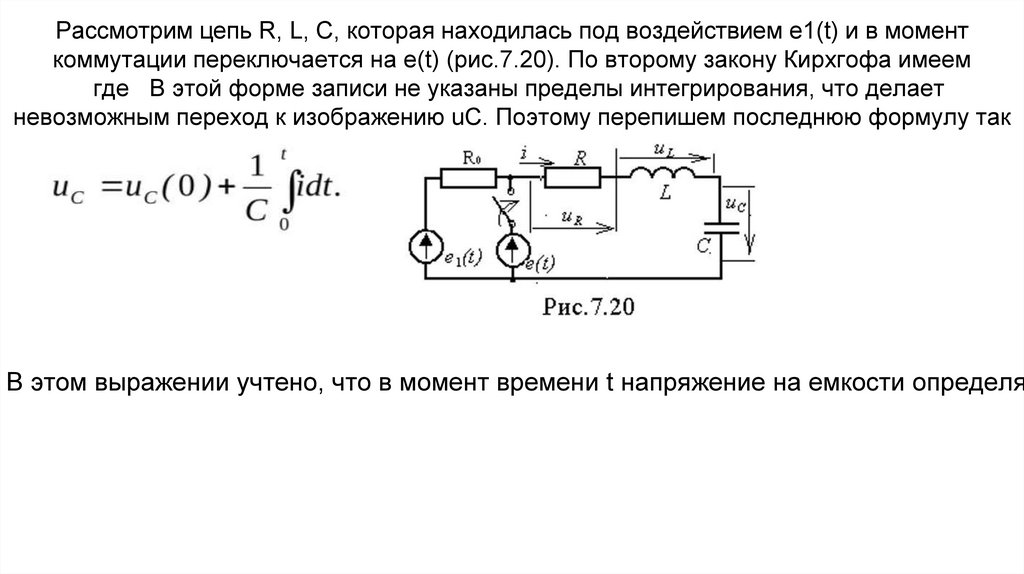
Рассмотрим цепь R, L, C, которая находилась под воздействием е1(t) и в момент
коммутации переключается на е(t) (рис.7.20). По второму закону Кирхгофа имеем
где В этой форме записи не указаны пределы интегрирования, что делает
невозможным переход к изображению uC. Поэтому перепишем последнюю формулу так
В этом выражении учтено, что в момент времени t напряжение на емкости определя

7.

Тогда
Чтобы перейти от оригиналов к изображениям умножим обе части этого
равенства на e-ptdt и проинтегрируем от 0 до .
Полагая i(t) I(p); e(t)
E(p) и учитывая каковы изображения постоянной величины (uC

8.

-это и есть закон Ома для цепи R, L, C в
операторной форме.
Выражение, стоящее в знаменателе, называется полным сопротивлением цепи R, L

9.

При нулевых начальных условиях (i(0)=0; uC(0)=0) закон Ома в операторной
форме имеет такой же вид, как и в комплексной форме.
Для любого узла разветвленной цепи во время ПП выражение первого закона
Кирхгофа для мгновенных значений имеет вид i1+i2+i3+…+in=0. Если перейти
от оригиналов к изображениям, то получим I1(p)+I2(p)+I3(p)+…+In(p)=0. Это
первый закон Кирхгофа в операторной форме, он имеет такой же вид как и в
комплексной форме.
При нулевых начальных условиях имеем
и это выражение аналогично второму закону Кирхгофа в комплексной форме.
Таким образом, законы Ома и Кирхгофа в операторной форме имеют такой же вид к

10.

Переходные процессы в
линейных электрических цепях

11.

Первый закон. В любой ветви с индуктивностью ток не может изменяться
скачком и в момент коммутации сохраняет то значение, которое он имел
непосредственно перед моментом коммутации
iL (0+) = iL (0-),
где iL (0+) - ток в ветви с индуктивностью в момент коммутации, сразу после комму
iL (0-) - ток в индуктивности непосредственно перед коммутацией.

12.

Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значе
uC (0+) = uC (0-),
где uC (0+) - напряжение на емкости в момент коммутации;
uC (0-) - напряжение на емкости непосредственно перед моментом комму

13.

В соответствии с классическим методом расчета, переходный ток в ветви схемы пре
где iпр(t) - принужденный ток, определяется в установившемся режиме после коммут
iсв(t) - свободный ток, определяется в схеме после коммутации, из которой ис

14.

Свободный ток определяют по формуле:
Количество слагаемых в формуле равно числу реактивных элементов (индуктивносте
P1, P2 - корни характеристического уравнения.
А1, А2 - постоянные интегрирования, определяются с помощью начальных услови
Начальные условия - это переходные токи и напряжения в момент коммутации, в
Начальные условия могут быть независимыми или зависимыми.

15.

Независимыми называют начальные условия, подчиняющиеся законам коммутации,
Остальные начальные условия: напряжение и ток в ветви с сопротивлением uR(0

16.

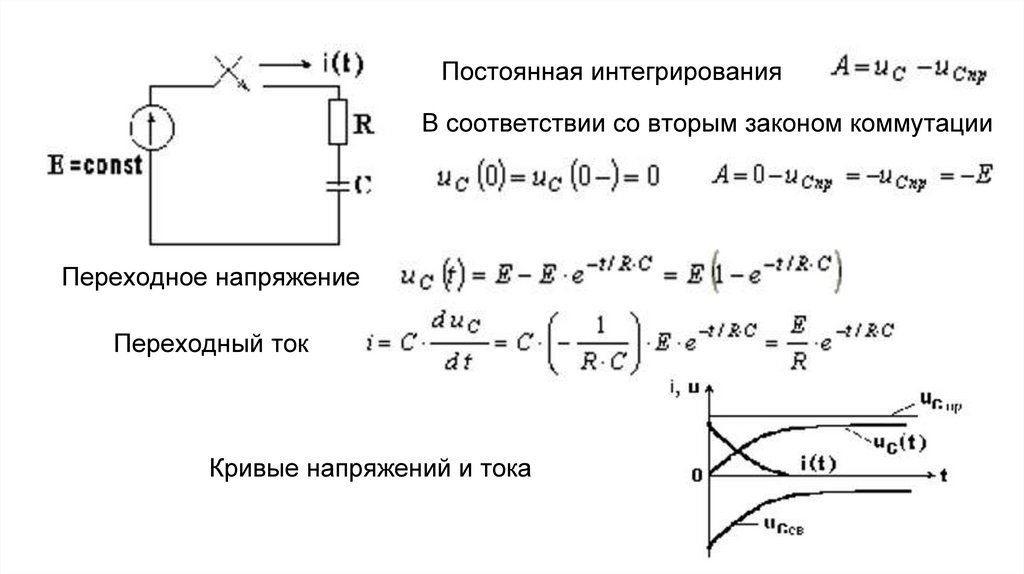
Подключение R-C цепи к источнику постоянной ЭДС
Полагаем, что до коммутации конденсатор не заряжен, напряжение на нем
uc(0-) = 0.
В результате коммутации рубильник замыкается, и конденсатор полностью
заряжается (рис. 8.7).
Принужденное напряжение на емкости равно ЭДС источника питания ucпр= E.
Переходное напряжение
В момент коммутации

17.

Постоянная интегрирования
В соответствии со вторым законом коммутации
Переходное напряжение
Переходный ток
Кривые напряжений и тока

18.

Анализ переходного процесса.
Принужденный и переходные
режимы.
Омск 2024
Жавнер А.А.
Буданцев С.С.