Similar presentations:
Определенный интеграл. Задача о вычислении площади криволинейной трапеции
1.
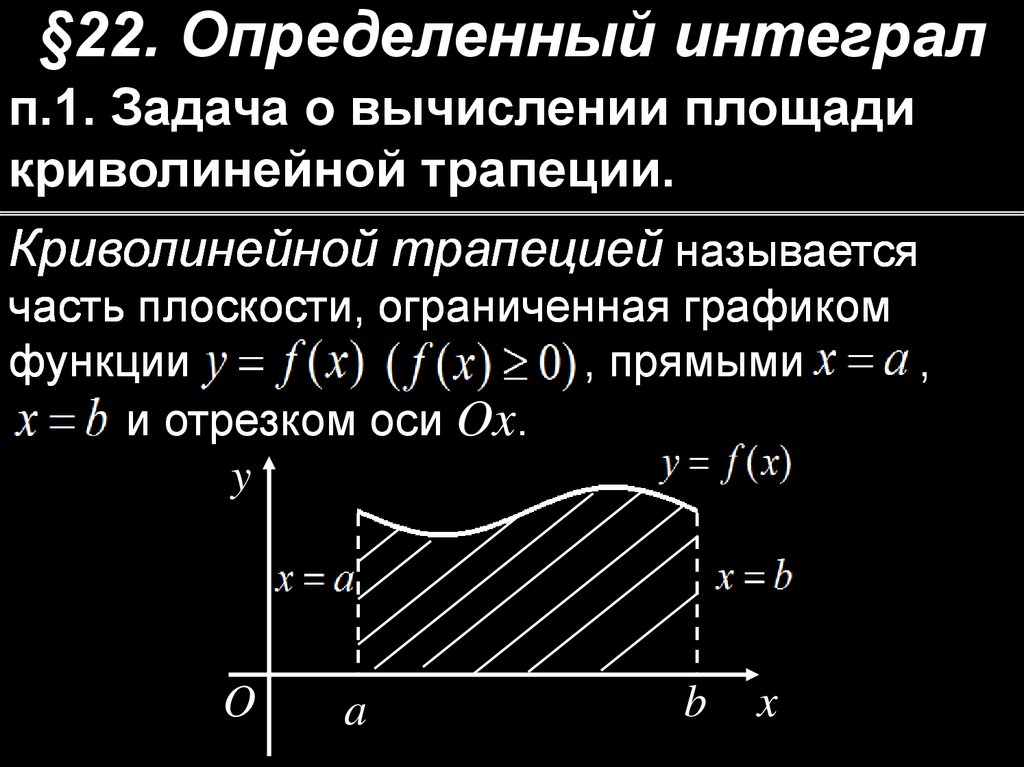
§22. Определенный интегралп.1. Задача о вычислении площади
криволинейной трапеции.
Криволинейной трапецией называется
часть плоскости, ограниченная графиком
функции
, прямыми
,
и отрезком оси Ox.
y
O
a
b
x
2.
yz1
O
a
z2
zi
zn
b
x
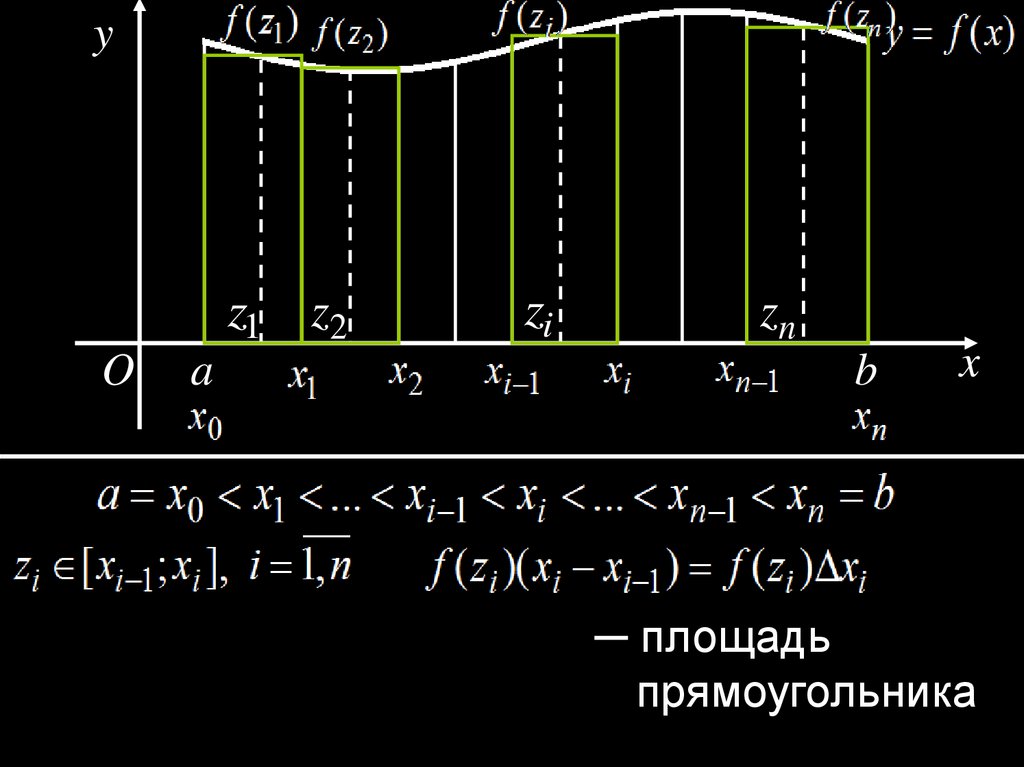
─ площадь
прямоугольника
3.
─ интегральная суммаС уменьшением
точность приближения
криволинейной трапеции ступенчатой фигурой
увеличивается.
4.
За точное значение площади S принимаетсяпредел интегральной суммы
, когда n
неограниченно возрастает так, что
5.
Если интегральная сумма имеет предел I,который не зависит ни от способа разбиения
отрезка
, ни от выбора точек , то этот
предел называется определенным интегралом
от функции
на отрезке
и
обозначается
6.
Геометрический смысл определенногоинтеграла
Определенный интеграл от неотрицательной
функции численно равен площади
криволинейной трапеции.
7.
п.2. Свойства определенногоинтеграла.
1.
8.
2.Доказательство.
9.
3.Доказательство.
10.
4.Доказательство.
─ разбиение отрезка
11.
5.Доказательство.
12.
6.Доказательство.
Св-во 3
Св-во 5
13.
7.Доказательство.
Св-во 6
Св-во 2
14.
15.
8.Теорема 1. (О среднем значении
определенного интеграла)
Пусть
функция
Тогда
существует точка
непрерывна на отрезке
такая, что
.
16.
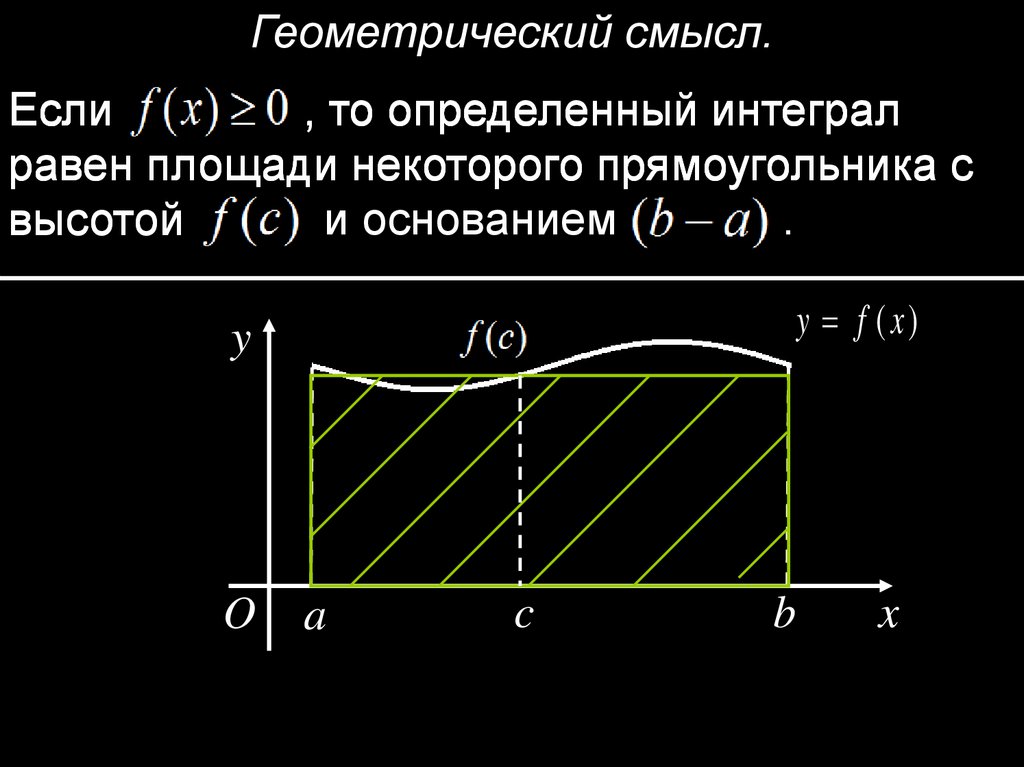
Геометрический смысл.Если
, то определенный интеграл
равен площади некоторого прямоугольника с
высотой
и основанием
.
y f (x)
y
O
a
c
b
x
17.
Доказательство.Вторая теорема Вейерштрасса §7
Св-во 7





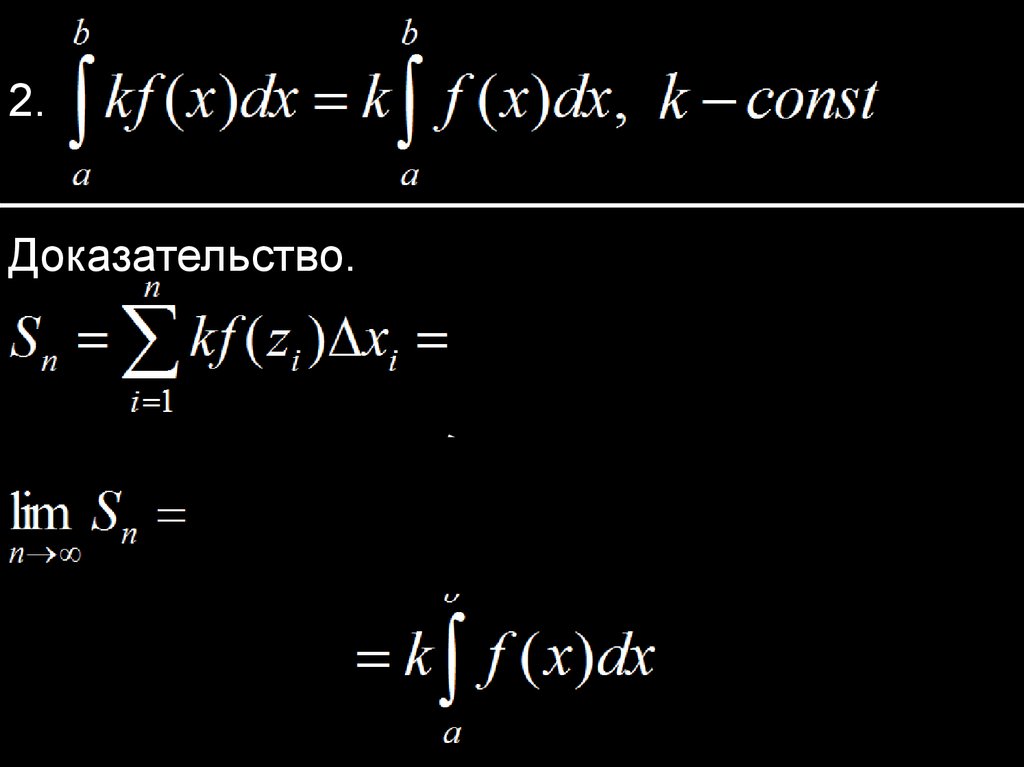
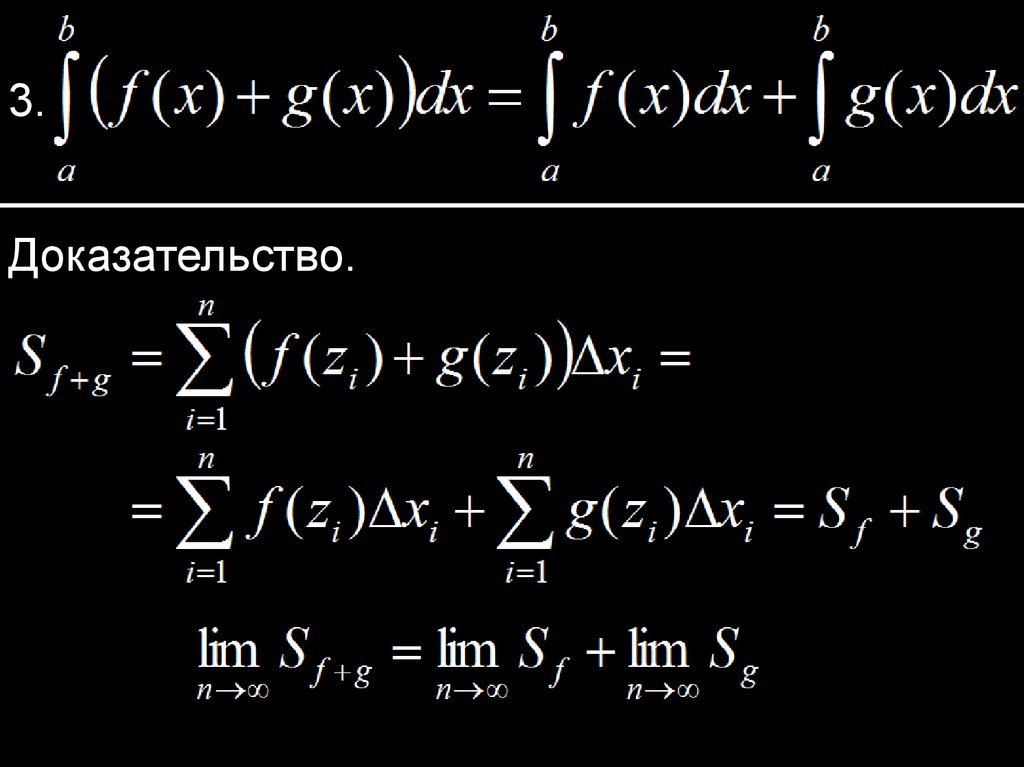


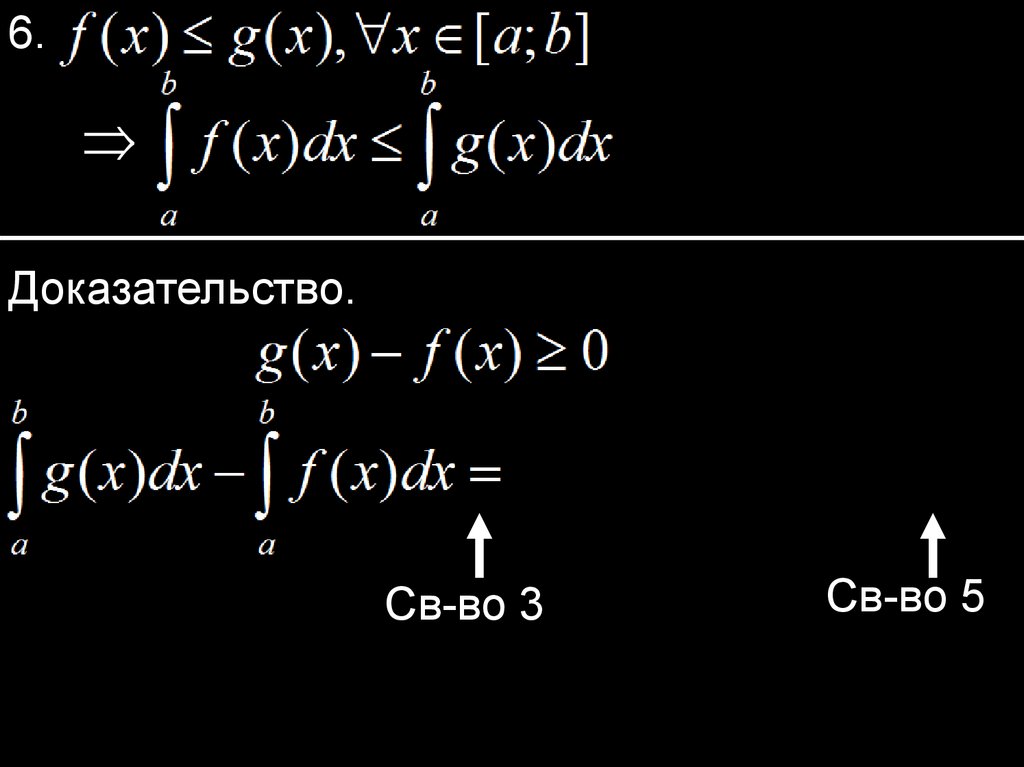
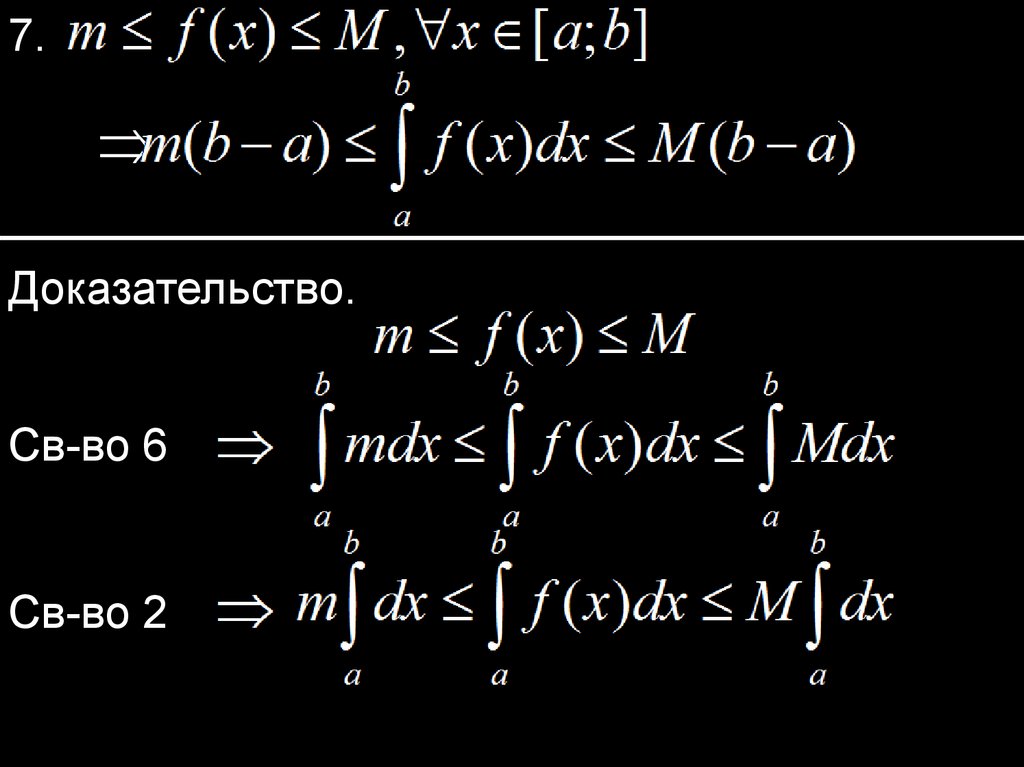
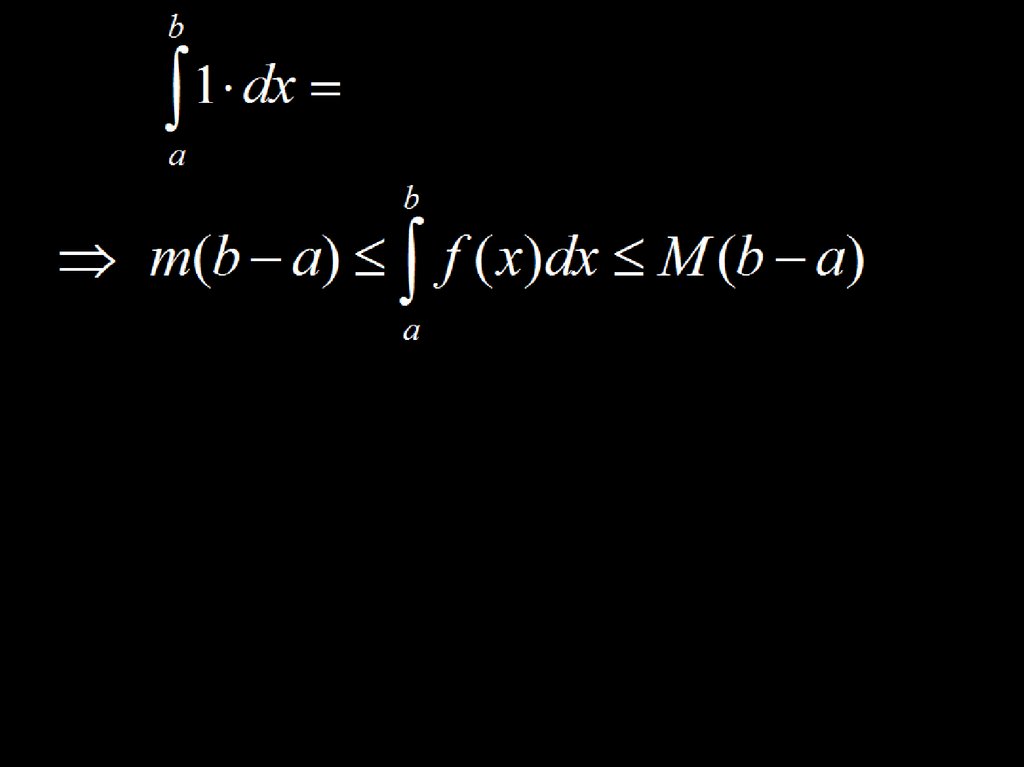


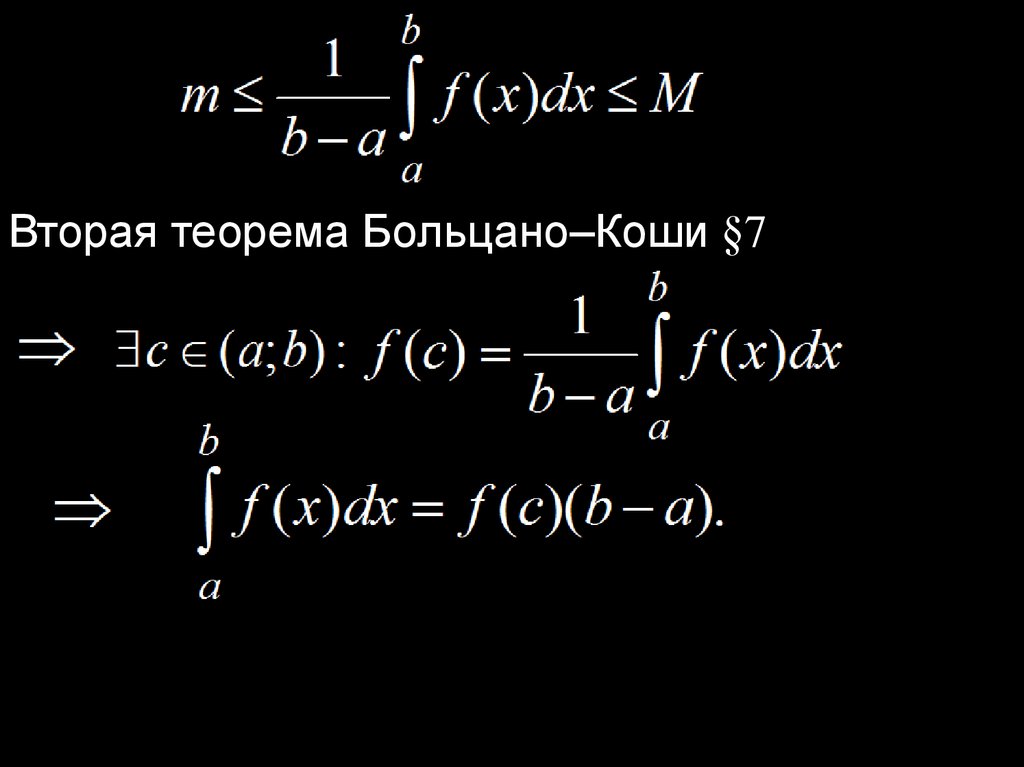
 mathematics
mathematics








