Similar presentations:
Площадь криволинейной трапеции. Определенный интеграл
1.
Урок 2Определенный интеграл.
Площадь криволинейной трапеции.
Три пути ведут к знанию:
путь размышления - это путь самый благородный,
путь подражания - это путь самый легкий,
и путь опыта - это путь самый трудный.
Конфуций
2.
Устно ответьте на вопрос задачи3.
Устно ответьте на вопрос задачи4.
Криволинейная трапецияФигура ограниченная графиком непрерывной и
неотрицательной функции
, осью абсцисс и прямыми
называется криволинейной трапецией.
Отрезок [a; b] называют основанием криволинейной трапеции.
У
х=а
x=b
y = f(x)
0
a
b
Х
5.
12
у
3
у
у
y = f(x)
y = f(x)
y = f(x)
У=1
х
х
Какие из предложенных фигур
являются криволинейными трапециями?
5
4
у
х
y = f(x)
у
6
y = f(x)
х
у
х
У=3
y = f(x)
х
6.
• Слово интеграл происходит от латинского словаinteger – «целый».
• Интеграция-восстановление, восполнение,
воссоединение; подробнее - это процесс,
ведущий к состоянию связанности отдельных
частей в целое. В построенной математической
модели речь идет о воссоединении целого по
отдельным частям (например о нахождении всей
площади – по площадям столбиков)
7.
Определенный интегралb
f ( x)dx F ( x)
b
a
F (b) F (a)
a
«определенный интеграл от a до b от функции f(x) по dx»
знак
интеграла,
f ( x) подынтегральная
функция ,
f ( x)dx подынтегральное
х переменная
F ( x) первообразная
a нижний
b верхний
выражение,
интегрирования,
подынтегральной
предел
предел
функции ,
интегрирования,
интегрирования
8.
Формула Ньютона-ЛейбницаS F (b) F (a)
b
S f ( x)dx
a
b
f ( x)dx F (b) F (a)
1643—1727
a
y f (x)
y
S
0
a
b
S F (b) F (a )
x
1646—1716
9.
Геометрический смысл определенного интеграла:Площадь фигуры S, ограниченной кривой y=f(x) ( f(x)>0 ),
b
осью абсцисс и прямыми x=a и x=b:
S f ( x)dx
a
10.
Вычислите площади фигур с рисунков 87 и 8811.
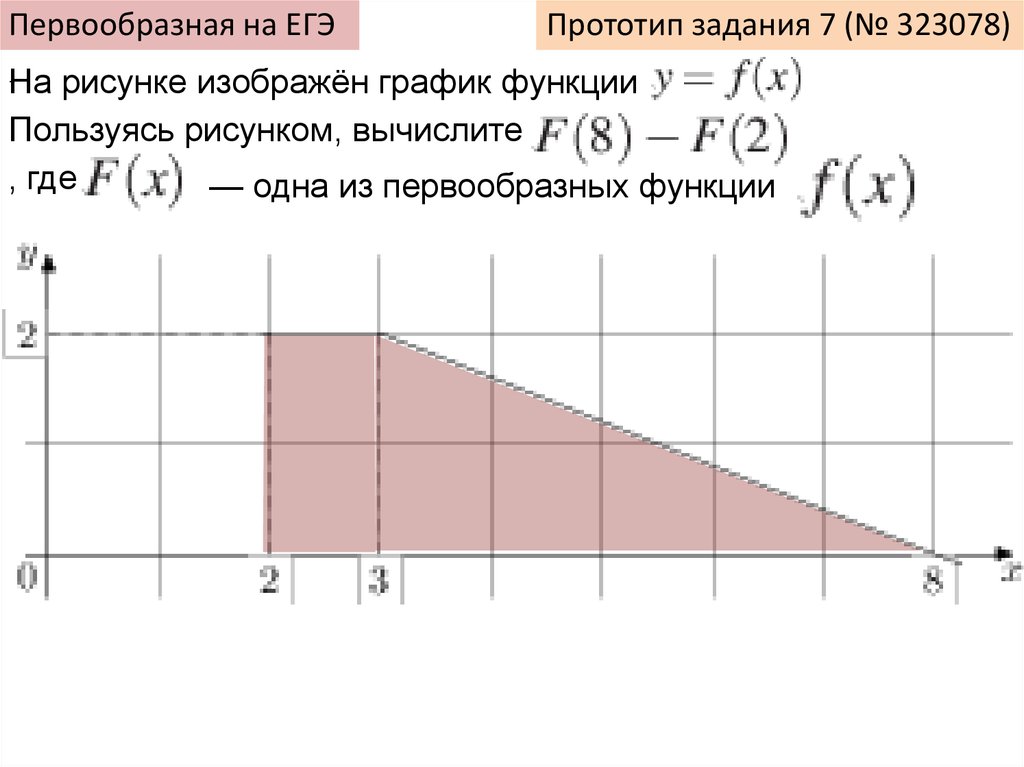
Первообразная на ЕГЭ.
Прототип задания 7 (№ 323078)
На рисунке изображён график функции
Пользуясь рисунком, вычислите
, где
— одна из первообразных функции
.
12.
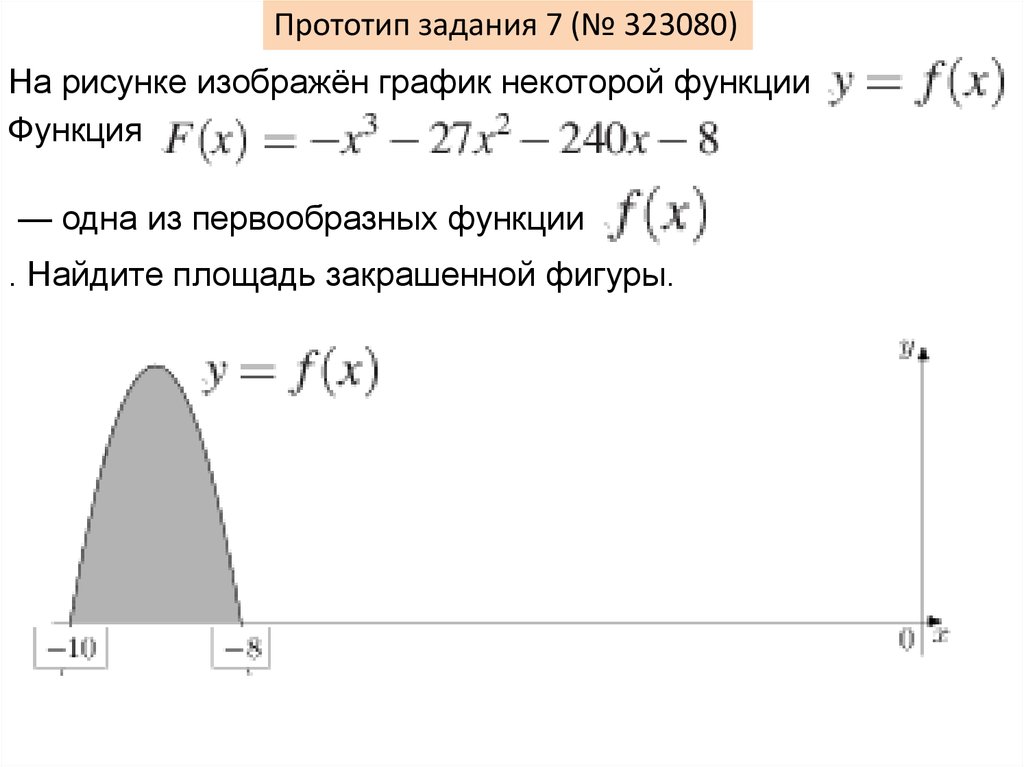
Прототип задания 7 (№ 323080)На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
13.
№ 323287 На рисунке изображён график некоторойфункции y=f(x).
Функция F(x)=2/3·x³+20x²+201x-6/7 — одна из первообразных
функции y=f(x).
Найдите площадь закрашенной фигуры.
y=f(x)
14.
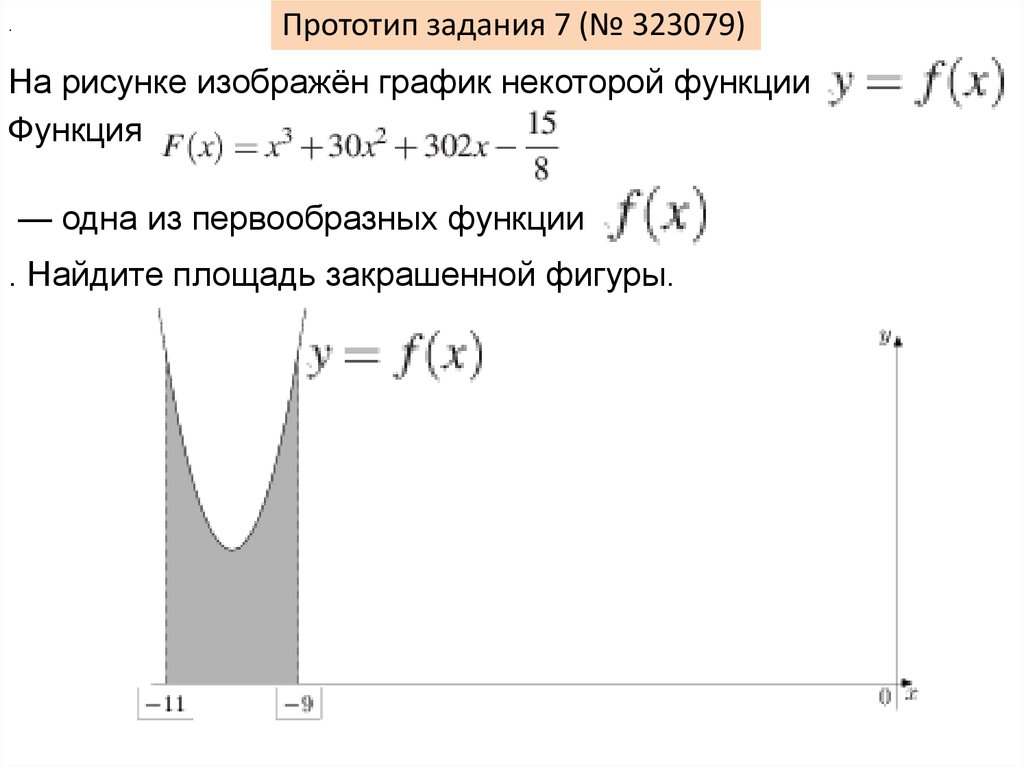
.Прототип задания 7 (№ 323079)
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
15.
1 способ9
S
f ( x)dx х
11
3
30 х 302 х
2
9
11
9 30 9 302 9 11 30 11 302 11
3
2
3
2
9 30 9 302 9 11 30 11 302 11
93 30 9 2 302 9 113 30 112 302 11
(113 93 ) (30 92 30 112 ) (302 11 302 9)
(11 9)(112 11 9 92 ) 30(92 112 ) 302(11 9)
2(11(11 9) 81) 30(9 11)(9 11) 302 2
2(11 20 81) 30 2 20 604 2(220 81) 1200 604
2 301 1200 604 602 1200 604 1206 1200 6
3
2
3
2
16.
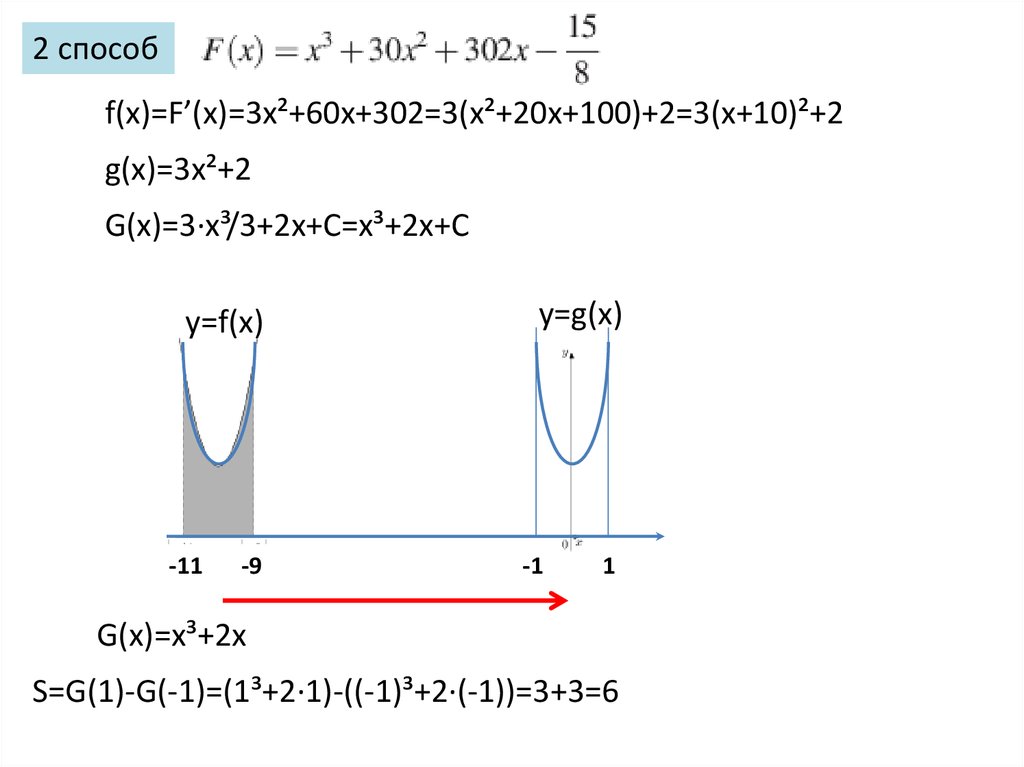
2 способf(x)=F’(x)=3x²+60x+302=3(x²+20x+100)+2=3(x+10)²+2
g(x)=3x²+2
G(x)=3·x³/3+2x+C=x³+2x+C
y=f(x)
-11
-9
y=g(x)
-1
1
G(x)=x³+2x
S=G(1)-G(-1)=(1³+2·1)-((-1)³+2·(-1))=3+3=6
17.
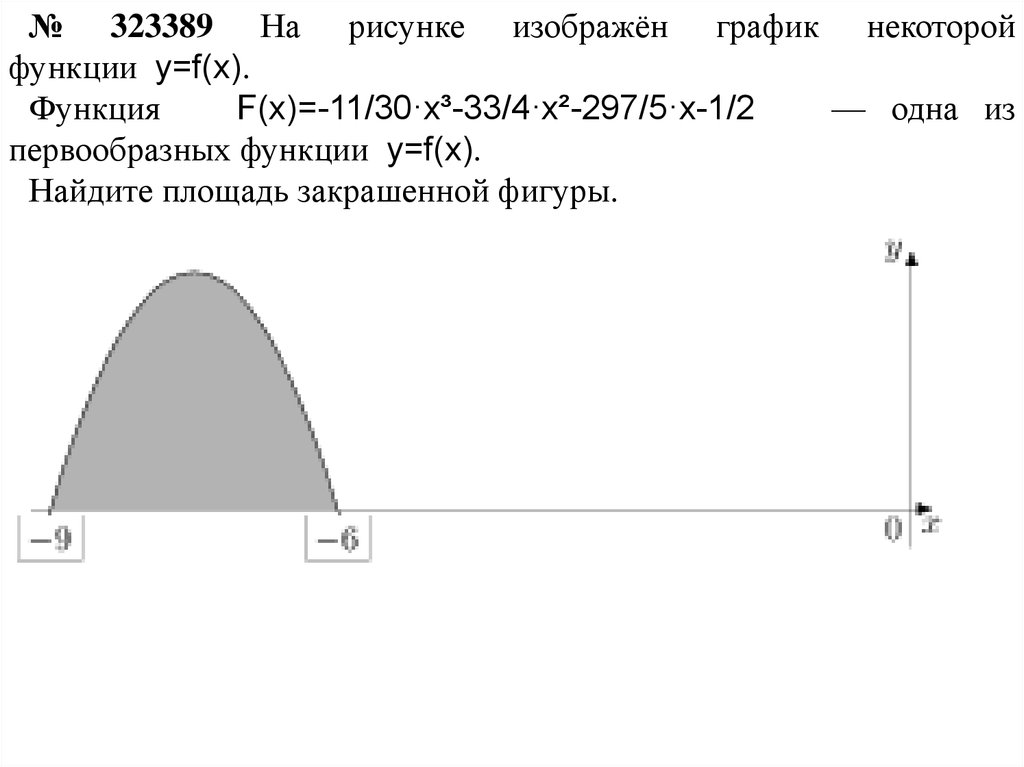
№ 323389 На рисунке изображён график некоторойфункции y=f(x).
Функция
F(x)=-11/30·x³-33/4·x²-297/5·x-1/2
— одна из
первообразных функции y=f(x).
Найдите площадь закрашенной фигуры.
18.
Домашнее задание с урока 2знать правила и формулы нахождения первообразных,
определение первообразной функции,
формулу Ньютона-Лейбница,
геометрический смысл определенного интеграла,
с сайта РЕШУ ЕГЭ выполнить 4 задачи на первообразную:
№ 323085, 323187, 323291, 323387.
Вольтер о Лейбнице
Весь мир его узнал по изданным трудам,
Был даже край родной с ним вынужден считаться,
Уроки мудрости давал он мудрецам,
Он был мудрее их: умел он сомневаться.
19.
Г.В. фон ЛейбницИ.Ньютон













 mathematics
mathematics








