Применение определенного интеграла для нахождения площади криволинейной трапеции

1. Применение определенного интеграла для нахождения площади криволинейной трапеции

2. Цель урока:

Ввести понятие интеграла и его вычисление по
формуле Ньютона – Лейбница, используя знания о
первообразной и правила её вычисления;
Проиллюстрировать практическое применение
интеграла на примерах нахождения площади
криволинейной трапеции;
Закрепить изученное в ходе выполнения
упражнений.

3.

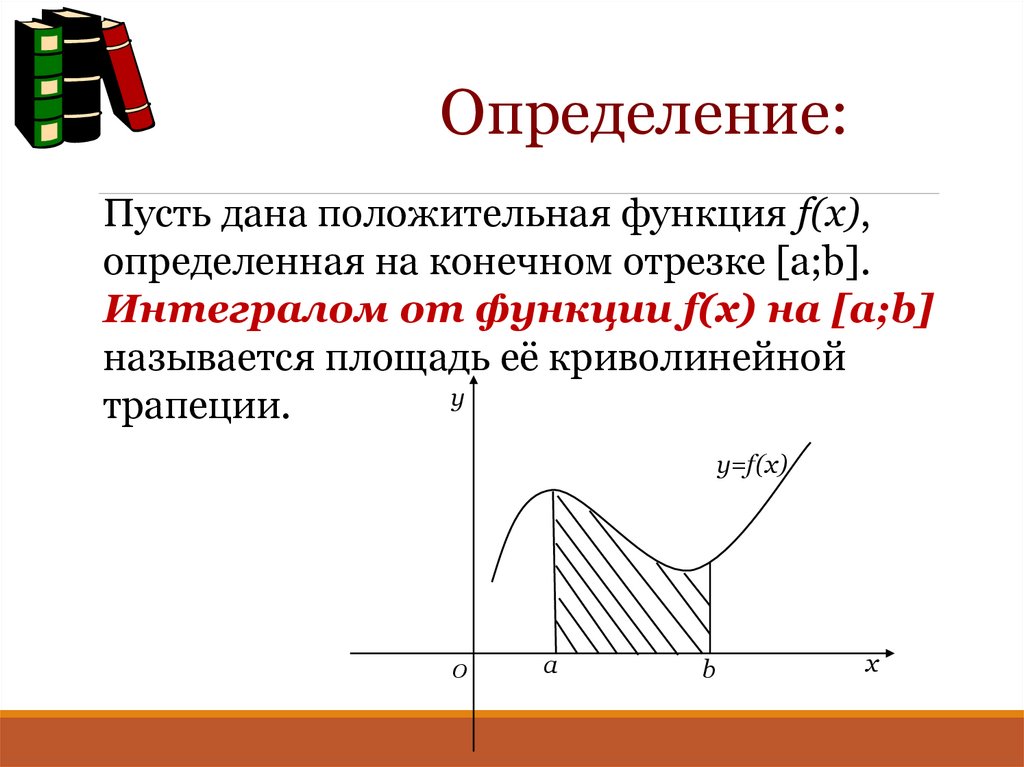
Определение:
Пусть дана положительная функция f(x),
определенная на конечном отрезке [a;b].
Интегралом от функции f(x) на [a;b]
называется площадь её криволинейной
y
трапеции.
y=f(x)
0
a
b
x

4. Обозначение:

«интеграл от a до b эф от икс дэ
икс»

5. Историческая справка:

Обозначение интеграла Лейбниц произвёл от
первой буквы слова «Сумма» (Summa).
Ньютон в своих работах не предложил
альтернативной символики интеграла, хотя
пробовал различные варианты. Сам термин
интеграл придумал Якоб Бернулли.
Готфрид Вильгельм
фон Лейбниц
Исаак Ньютон
Якоб Бернулли

6. Историческая справка:

Оформление определённого интеграла в привычном нам виде
придумал Фурье.
Обозначение неопределённого интеграла ввёл Эйлер.
Леонард Эйлер
Жан Батист Жозеф Фурье

7.

Формула Ньютона - Лейбница

8.

Пример 1.
Вычислить определённый интеграл:
Решение:
=

9.

Пример 2.
Вычислите определённые интегралы:
5
9
1

10.

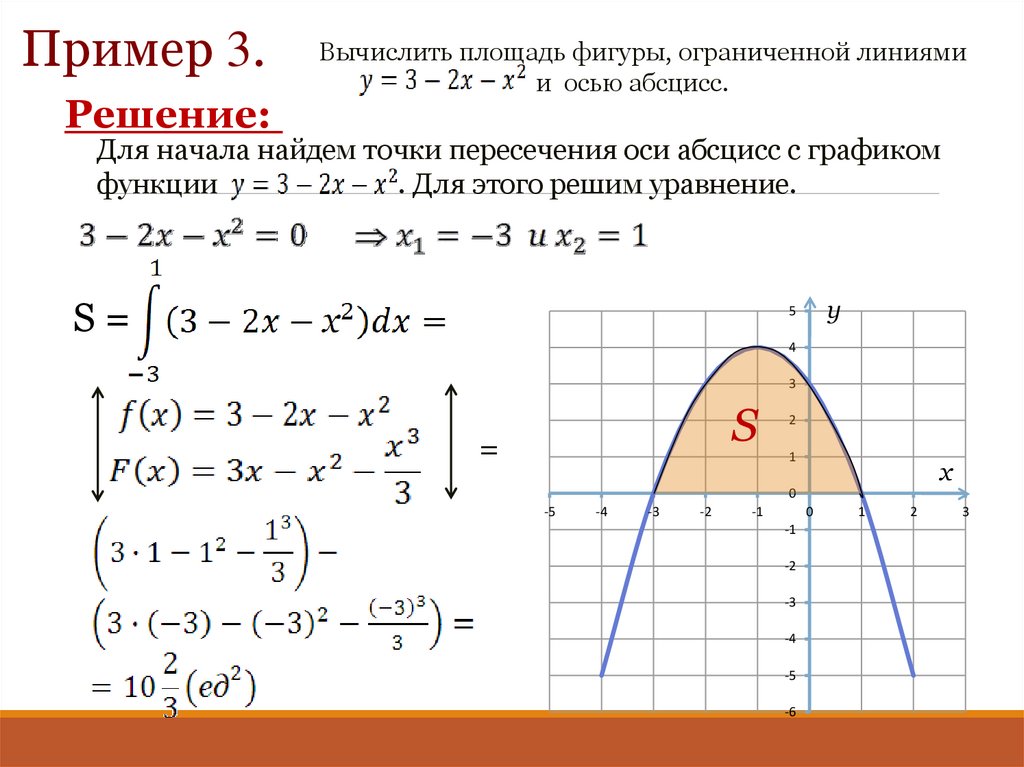
Пример 3.
Решение:
Вычислить площадь фигуры, ограниченной линиями
и осью абсцисс.
Для начала найдем точки пересечения оси абсцисс с графиком
функции
. Для этого решим уравнение.
S=
y
5
4
3
S
=
2
1
x
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
-6
1
2
3

11.

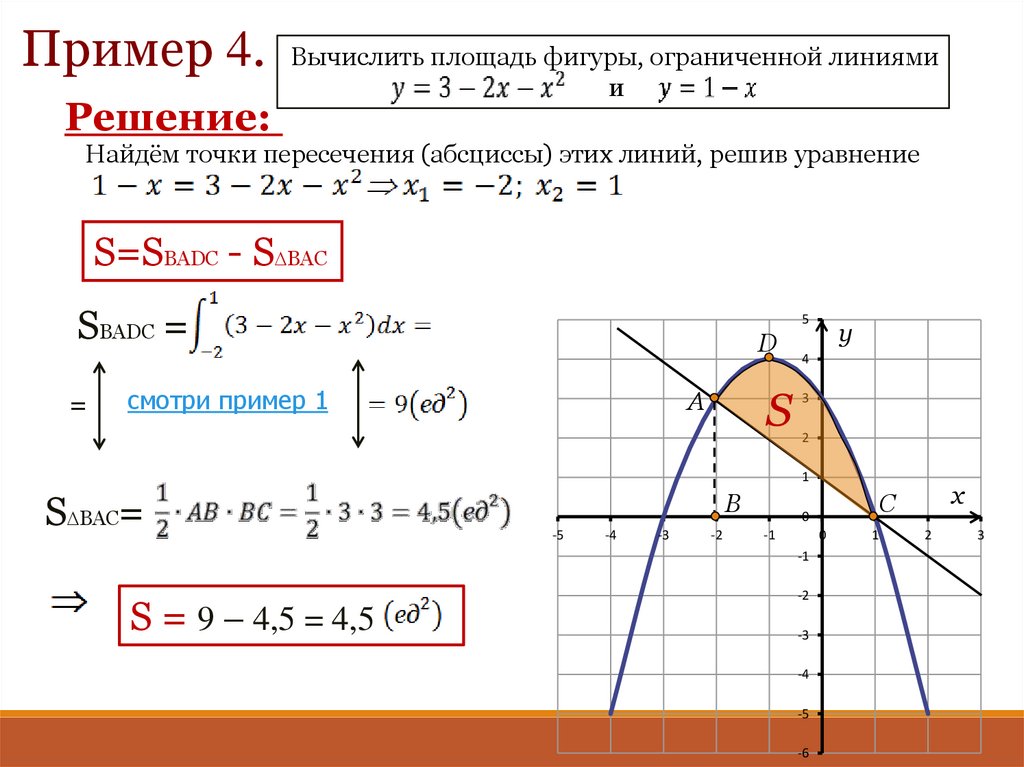
Пример 4.
Решение:
Вычислить площадь фигуры, ограниченной линиями
и
Найдём точки пересечения (абсциссы) этих линий, решив уравнение
S=SBADC - S BAC
SBADC =
=
5
D
смотри пример 1
S
A
y
4
3
2
1
S BAC=
B
-5
-4
-3
-2
-1
0
-1
S = 9 – 4,5 = 4,5
-2
-3
-4
-5
-6
x
C
0
1
2
3

12.

Составление карточек-консультаций, таблиц на тему:
«Вычисление интегралов. Формула Ньютона—Лейбница»

13.

Пример 5.
Решение:
Найти площадь фигуры, ограниченной кривой
у = х3; х = 0; х = 2 и осью 0Х
Фигура, ограниченная кривой у = х3; прямыми х = 0; х = 2 и осью 0Х криволинейная трапеция (по определению), площадь этой фигуры
можно вычислить по формуле.
Ответ: S = 4 кв.ед.
2

14.

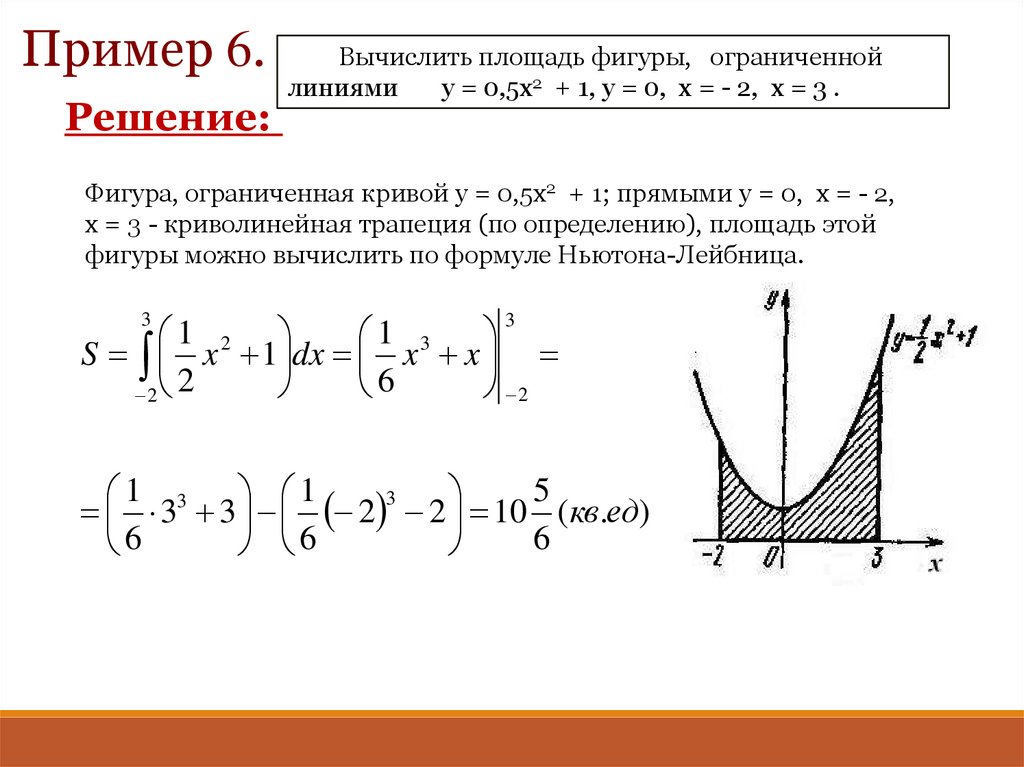
Пример 6.
Решение:
Вычислить площадь фигуры, ограниченной
линиями
y = 0,5х2 + 1, y = 0, х = - 2, x = 3 .
Фигура, ограниченная кривой y = 0,5х2 + 1; прямыми y = 0, х = - 2,
x = 3 - криволинейная трапеция (по определению), площадь этой
фигуры можно вычислить по формуле Ньютона-Лейбница.
3
1 2
1 3
S x 1 dx x x
2
6
2
2
3
5
1
1
3
33 3 2 2 10 (кв.ед)
6
6
6

15.

Фигура ограничена графиком непрерывной и неположительной
на отрезке [а; b] функции f(х), осью Ох и прямыми х = а, х = b.
Рассмотрим функцию
– f(x). Фигура аА1В1b
симметрична фигуре аАВb относительно оси Ох, а
следовательно, их площади S1 и S равны. Но
S1
b
b
a
a
f x dx f x dx

16.

Пример 7.
Решение:
Вычислить площадь фигуры, ограниченной
линиями y = - х2 - 1, у = 0, х =-1, х = 2.
Используем следующее свойство определенного
интеграла для нахождения площади
криволинейной трапеции:
b
S f x dx
a
2
S x 1 dx
1
2
x
2
2
1 dx
1
2
1
3
1 3
1
3
x x 2 2 1 1 6(кв.ед)
3
1 3
3

17.

Вычислите определенные интегралы
Задание
Ответ
4
18
1
6

18.

Найдите площади криволинейной
трапеции:

19.

20.

Пример 1.
Вычислить определённый интеграл:
Решение:
=
пример 4