Определённый интеграл. Вычисление площади криволинейной трапеции

1.

Определённый интеграл.
Вычисление площади
криволинейной трапеции

2.

ПОВТОРИМ!
1. Функция F(х) называется первообразной функции
f(x) на некотором промежутке, если для всех Х из
этого промежутка выполняется равенство:
F ( x ) f ( x )
Другими словами нахождение первообразной – это
обратное действие нахождения производной.
2. F(x)+C, где С произвольная постоянная (любое
число), называется семейством первообразных.
3. Совокупность всех первообразных данной функции
f(x) называется неопределённым интегралом и
обозначается:
f ( x ) dx F ( x ) C

3.

Таблица первообразных
Правила нахождения первообразных
f ( x) g ( x) F ( x) G ( x) C
kf ( x ) kF ( x ) C
1
f ( kx b) F ( kx b) C
k

4.

Найди ошибку в вычислении первообразных
1) f ( x) x
5
F ( x) 5 x C
4
2) f ( x) 6 x
1 7
F ( x) x
7
3) f ( x) x
1 5
F ( x) x
5
4
6
x
F ( x) C
6
F ( x) 3 x 2 C
5
x
F ( x) C
5

5.

Найдите первообразную функции
1) F ( x) x 2 C
1) f ( x) 2 x
2) f ( x) 2 sin x e
x
2) F ( x) 2 cos x e x C
3) f ( x) 25 x 3
3) F ( x) 5 x 3x
4) f ( x) x
2 3
4) F ( x )
x C
3
4
5) f ( x) (3x 1)
4
5
1
5) F ( x) (3 x 1) 5 C
15

6.

Понятие криволинейной трапеции
Фигура, ограниченная неотрицательной на отрезке
[a;b] функцией y=f(x) и прямыми у=0, x=a, x=b
называется
криволинейной трапецией.

7.

Вычисление площади криволинейной трапеции
Разобьем отрезок [а;b]
точками деления
х1, х2 …хk…xn-1 на n равных
частей. При этом х0 = а, хn = b
Рассмотрим прямоугольник с
основанием хk xk+1
Заменим площадь
криволинейной трапеции на
этом участке площадью этого
прямоугольника.
Sk = f(xk) ∙ ∆x, где ∆x = xk+1 - хk
Сделаем это на каждом
маленьком отрезке.
Тогда площадь
криволинейной трапеции
приближенно равна площади
ступенчатой фигуры
Sn ≈ f(x0)∙∆x + f(x1)∙∆x +
…f(xk)∙∆x + … + f(xn)∙∆x

8.

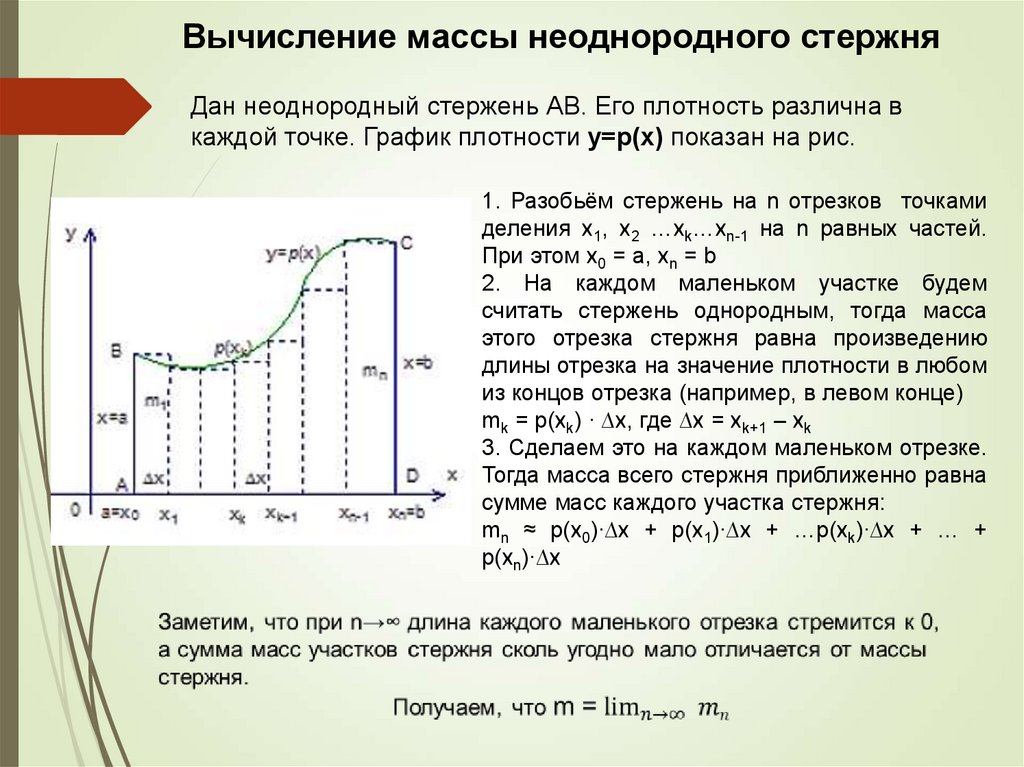
Вычисление массы неоднородного стержня
Дан неоднородный стержень АВ. Его плотность различна в
каждой точке. График плотности у=р(х) показан на рис.
1. Разобьём стержень на n отрезков точками
деления х1, х2 …хk…xn-1 на n равных частей.
При этом х0 = а, хn = b
2. На каждом маленьком участке будем
считать стержень однородным, тогда масса
этого отрезка стержня равна произведению
длины отрезка на значение плотности в любом
из концов отрезка (например, в левом конце)
mk = р(xk) ∙ ∆x, где ∆x = xk+1 – хk
3. Сделаем это на каждом маленьком отрезке.
Тогда масса всего стержня приближенно равна
сумме масс каждого участка стержня:
mn ≈ p(x0)∙∆x + p(x1)∙∆x + …p(xk)∙∆x + … +
p(xn)∙∆x

9.

Обобщение. Определение интеграла
Верхний предел
интегрирования
Нижний предел
интегрирования
b
f
(
x
)
dx
Подынтегральная
функция
a
Подынтегральное
выражение
Геометрический смысл определенного интеграла – площадь
криволинейной трапеции под графиком подынтегральной функции

10. Вопрос:

Оказывается, есть прямая связь между
этими понятиями!

11.

Формула Ньютона-Лейбница
Площадь криволинейной трапеции можно вычислить
по формуле:
S F (b ) F ( a )
Где F(x) – первообразная функции y=f(x)
Вычисление площади криволинейной трапеции
сводится к отысканию первообразной F(x)
функции f(x), то есть к интегрированию функции
f(x).

12.

Формула Ньютона - Лейбница
b
f ( x)dx F (b) F (a )
a
Таким образом:
Исаак Ньютон
1642-1727
Готфрид Лейбниц
1646-1716 гг.

13.

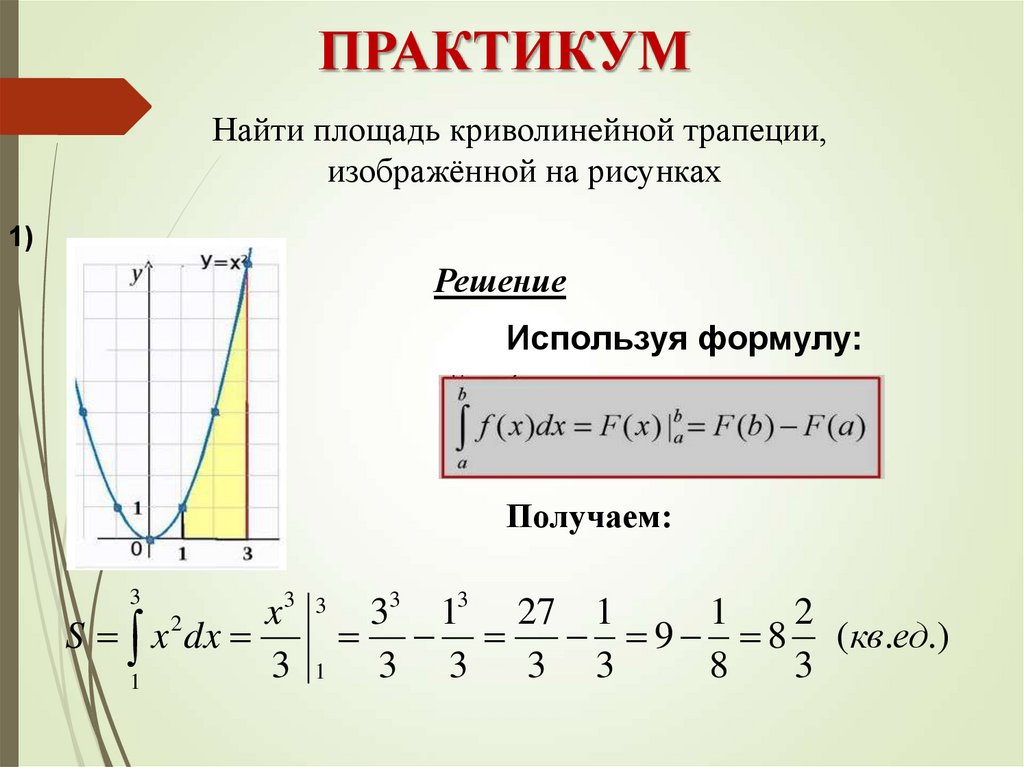
ПРАКТИКУМ
Найти площадь криволинейной трапеции,
изображённой на рисунках
1)
Решение
Используя формулу:
Получаем:
3
3 3
3
3
x
3
1
27 1
1
2
2
S x dx
9 8 (кв.ед.)
3 1 3 3
3 3
8
3
1

14.

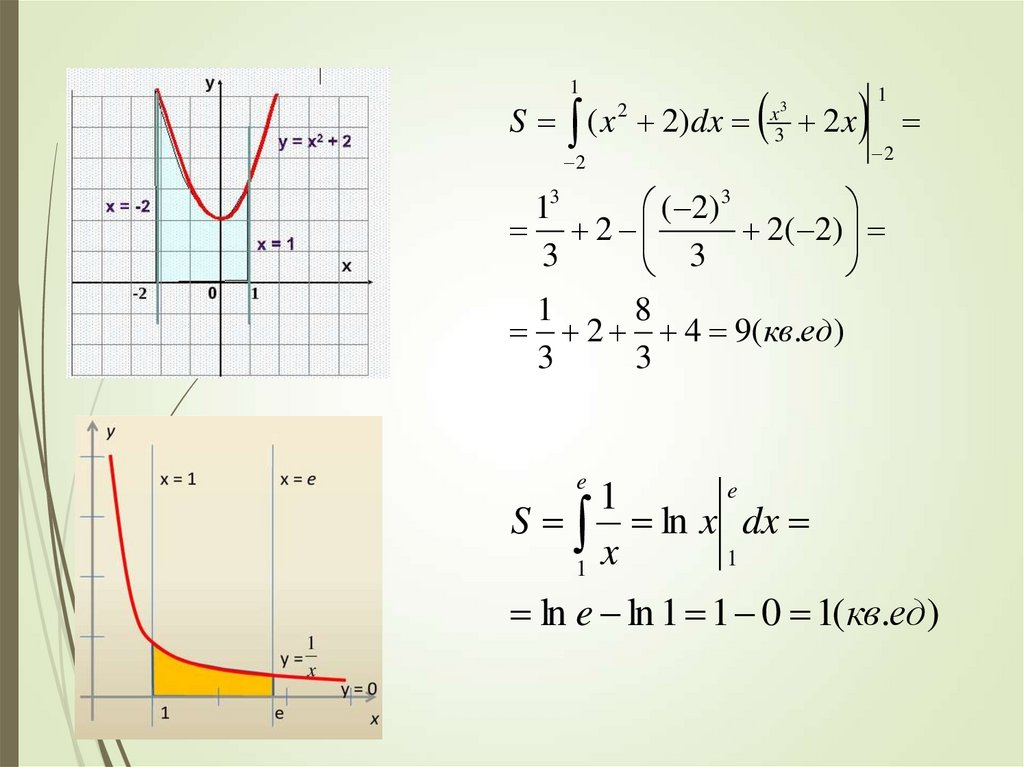
1
S ( x 2)dx
2
2x
x3
3
2
1
2
( 2) 3
13
2
2( 2)
3
3
1
8
2 4 9(кв.ед)
3
3
e
e
1
S ln x dx
x
1
1
ln e ln 1 1 0 1(кв.ед)

15.

Вычисление площадей с помощью
интегралов
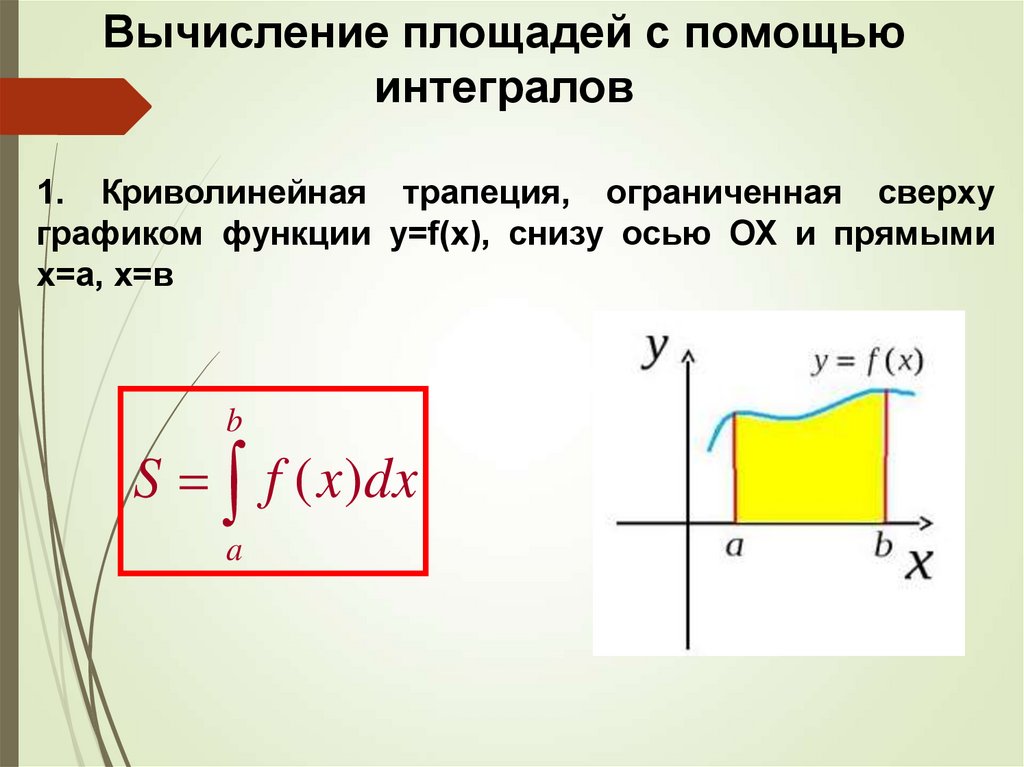
1. Криволинейная трапеция, ограниченная сверху
графиком функции y=f(x), снизу осью ОХ и прямыми
х=а, х=в
b
S f ( x )dx
a

16.

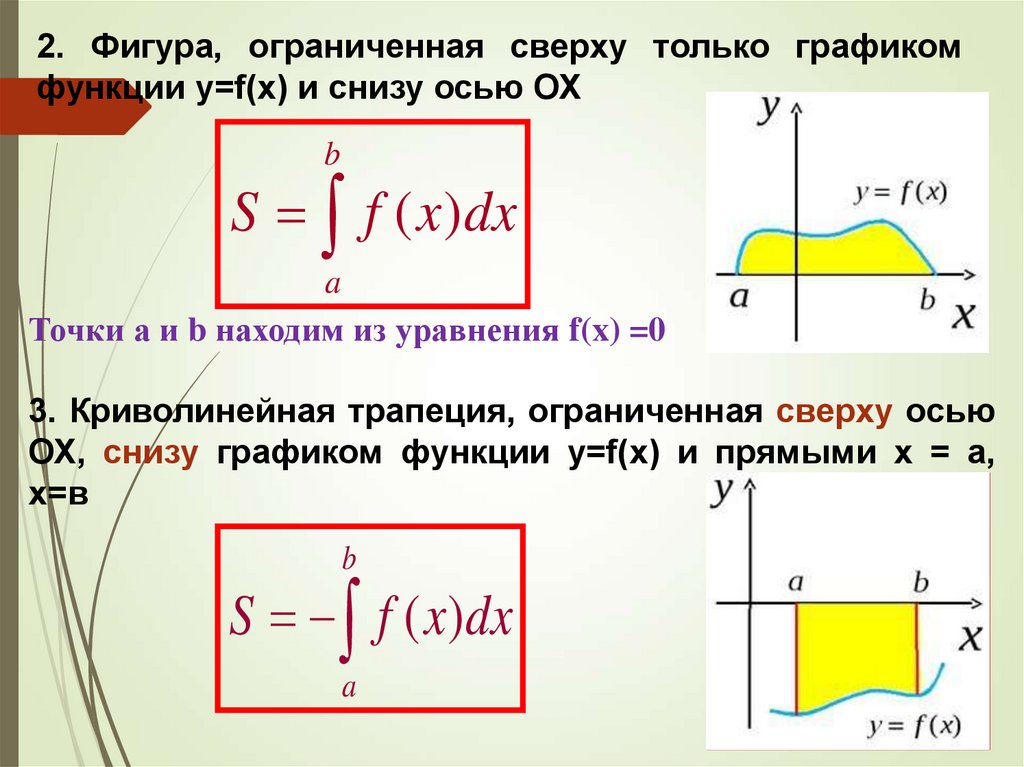
2. Фигура, ограниченная сверху только графиком
функции y=f(x) и снизу осью ОХ
b
S f ( x ) dx
a
Точки а и b находим из уравнения f(x) =0
3. Криволинейная трапеция, ограниченная сверху осью
ОХ, снизу графиком функции y=f(x) и прямыми х = а,
х=в
b
S f ( x )dx
a

17.

4. Фигура, ограниченная сверху двумя графиками
функций y=f(x) и g(x), снизу осью ОХ и прямыми х=а, х=в
с
b
a
с
S f ( x ) dx g ( x ) dx
Точку С находим из уравнения f(x)=g(x)
5. Фигура, ограниченная сверху графиком функции
y=f(x), снизу графиком функции y=g(x)
b
S ( f ( x ) g ( x )) dx
a
Точки a и b находим из уравнения
f(x)=g(x)

18.

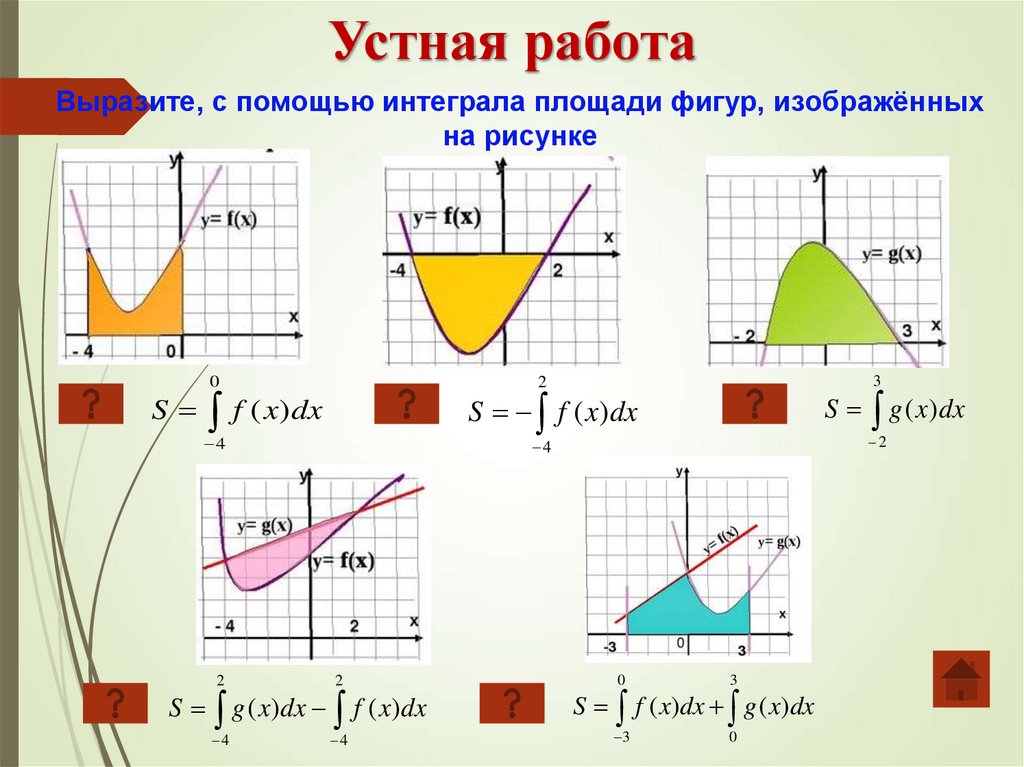
Устная работа
Выразите, с помощью интеграла площади фигур, изображённых
на рисунке
0
3
2
S f ( x ) dx
S g ( x ) dx
S f ( x)dx
4
2
4
2
2
4
4
S g ( x) dx f ( x)dx
0
3
3
0
S f ( x)dx g ( x)dx

19.

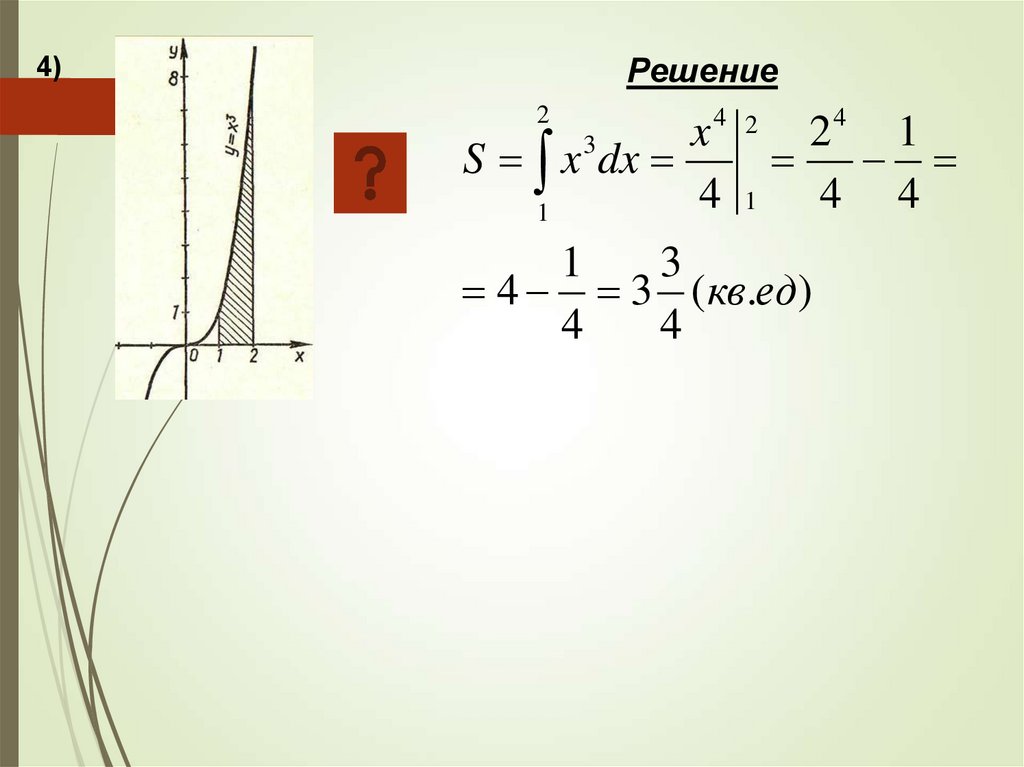
Решение
4)
2
4 2
4
x
2
1
3
S x dx
4 1 4 4
1
1
3
4 3 (кв.ед)
4
4

20.

y 4 x 2 , y 3x, y 0
6)
находится в I четверти
Решение
3x 2 1
x3 2
S 3xdx (4 x )dx
4 x
2
3 1
0
0
1
1
2
2
3 8
1 19
1
8 4 3 (кв.ед)
2 3
3 6
6
Решение
7)
x2
1 x3 1
S ( x 2)dx x dx
2 x
2
2 3 2
2
2
3
1 8 3
1
6 6 3 4 (кв.ед)
2
3 3 2
2
1
1
2

21. Задание (ПРЗ): по готовым рисункам найти площадь фигур. Решения записать в тетради.

22.

Домашнее задание
Вычислить площадь фигуры, ограниченной линиями,
предварительно сделав рисунок
1) y x ( x 0), y 1, y 4, x 0
2
2) y x 4 x 8, y 3x x , если x [ 2;3]
3) y 3x 1, y 9 x
2
2
3
4) y x 4 x 2 4, y 10, x 3, x 0
5) y x, y 5 x, x 1, x 2
6) y x 2 4 x 2, y x 2
7) y sin x, x
6
,x
3

23.

Подведём итоги
1. Познакомились с понятиями криволинейной
трапеции и определённого интеграла.
2. Научились вычислять по формуле НьютонаЛейбница площадь криволинейной трапеции,
используя знания о первообразной и правила её
вычисления.
3. Закрепили
изученное
практических заданий.
в
ходе
выполнения