Определенный интеграл. Задача о вычислении площади плоской фигуры (лекция 2.2)

1.

Определенный интеграл
Лекция 2.2

2.

Задача о вычислении площади
плоской фигуры
Решим задачу о вычислении площади
фигуры, ограниченной графиком функции
y f x , отрезками прямых
x a , x b и осью Ox.Такую фигуру
называют криволинейной трапецией
y
A
a=x0 x1 x2
y=f(x)
B
xn-1 b=xn x

3.

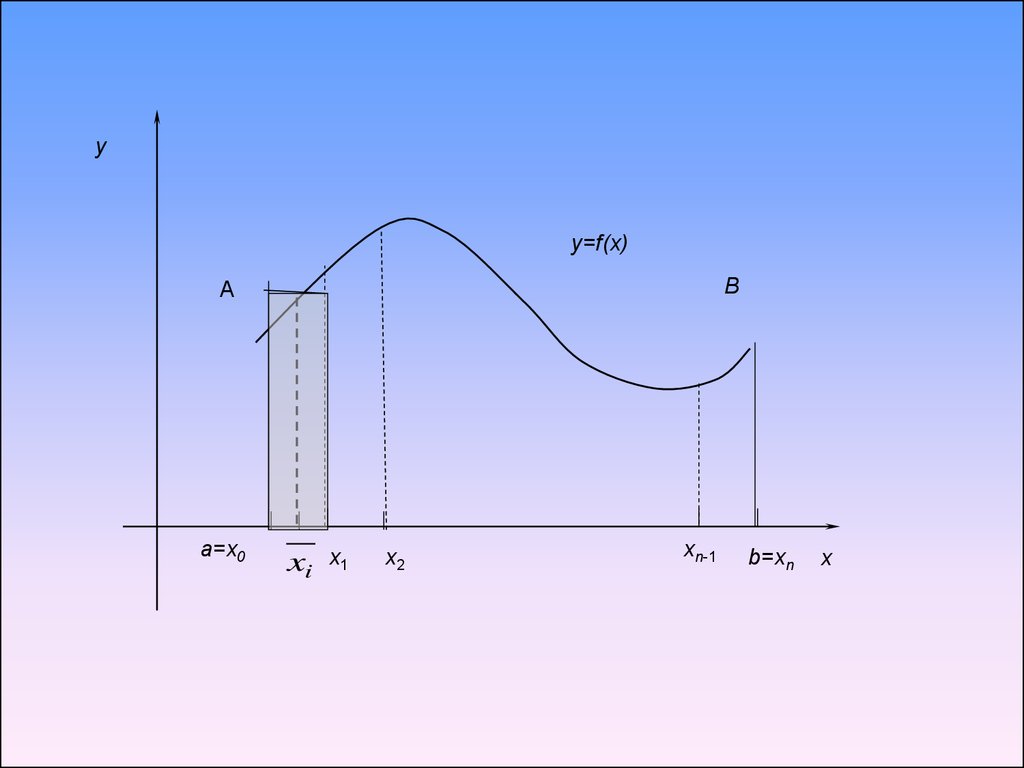
Задача о вычислении площади плоской
фигуры
Разобьем отрезок a, b на n частей
точками a x0 , x1, x2 ,..., xi 1, xi ,..., xn b .
При этом криволинейная трапеция разобьется
на n элементарных криволинейных
трапеций. Заменим каждую такую
криволинейную трапецию прямоугольником с
основанием xi xi xi 1 , где i 1,2,.., n и
высотой h f xi , где xi -произвольно
выбранная внутри отрезка xi 1, xi точка.

4.

y
y=f(x)
B
A
a=x0
xi x1
x2
xn-1
b=xn
x

5.

Задача о вычислении площади плоской
фигуры
Площадь прямоугольника будет
равна Si f xi xi , а площадь
всей криволинейной фигуры
приблизительно будет равна
сумме площадей всех
прямоугольников:
n
n
i 1
i 1
S Si f xi xi .

6.

Определенный интеграл
Определение.
n
Выражение f xi xi , где
i 1
xi xi xi 1 , называется
интегральной суммой функции f x
на отрезке a, b .

7. Определенный интеграл

Определение.
Если существует конечный
n
lim
f xi xi , не
max xi 0 i 1
зависящий ни от способа разбиения отрезка
a, b на части, ни от выбора точек xi xi 1 , xi ,
то этот предел называется определенным
интегралом функции f x на отрезке a, b и
b
обозначается f x dx .
a

8. Определенный интеграл

Замечание.
С геометрической точки зрения
b
при f x 0 f x dx равен
a
площади криволинейной
трапеции

9. Свойства определенного интеграла

a
1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a

10. Свойства определенного интеграла

b
b
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a

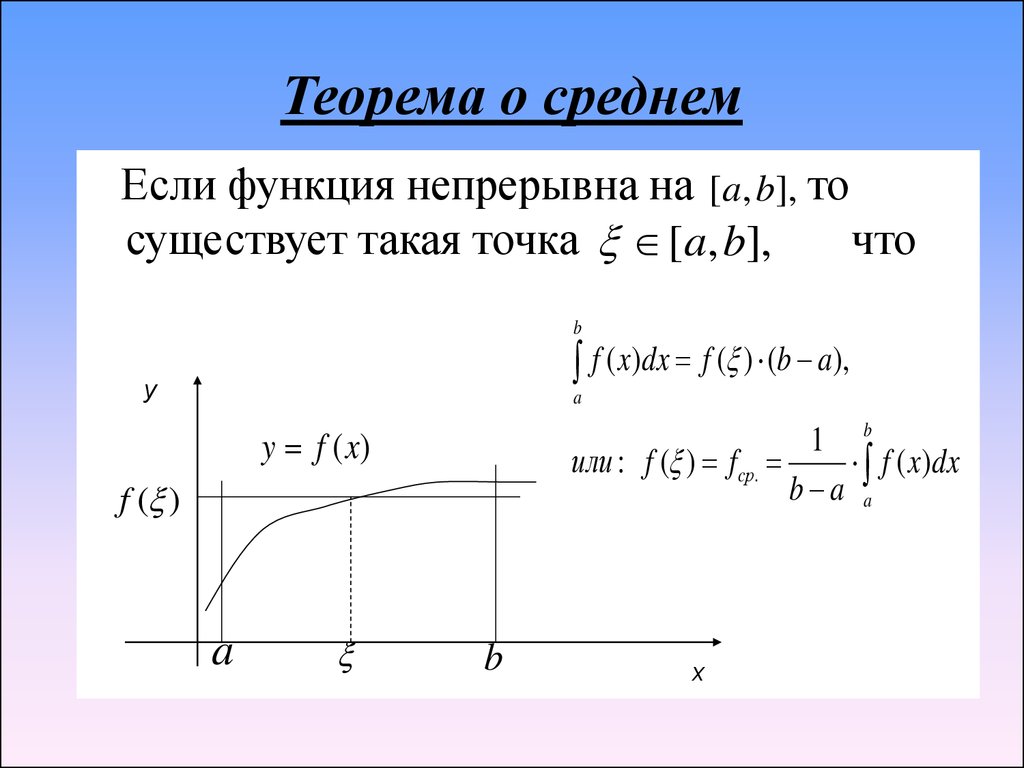
11. Теорема о среднем

Если функция непрерывна на [a, b], то
существует такая точка [a, b],
что
b
x
f ( x)dx f ( ) (b a),
y
a
y f (x)
1 b
или : f ( ) f cр.
f ( x)dx
b a a
y
f ( )
a
b
x

12. Вычисление определенного интеграла

Теорема.
Пусть F x - первообразная функции f x .
b
Тогда f x dx F b F a .
a
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.

13. Пример

Вычислить
3
e x dx
0
3
e dx e
x
x 3
0
0
e e e 1
3
0
3

14. Вычисление интеграла

Теорема (Замена переменной в
определенном интеграле).
Пусть f x непрерывна на a, b , а
функция x t непрерывна вместе
со своей производной t на
отрезке , , причем a ,
b . Тогда
b
a
f x dx f t t dt .

15. Пример

x 1 t
x 1 t 2
3
2
t
1
x t 2 1, dx 2tdt
2tdt
t
1
x 1
x 0, t 1
2
xdx
0
x 3, t 2
2
t
8 1
2 t 1 dt 2 t 1 dt 2
t 2 2 1
3
1
1
3 3
1
2
2
2
2
3
1 7
4 8
8
2 2 1 2 1 2
3 3
3 3
3

16.

Теорема (интегрирование по
частям в определенном
интеграле).
Если функции u u x , v v x и их
производные u x и
v x непрерывны на отрезке a, b , то
b
b
a
a
b
udv u v vdu .
a

17. Пример

dx
u ln x, du
e e dx
x x ln x 1 x
ln xdx
x
1
1
dv dx, v x
e
x ln
e
x1
e
e
dx e ln e ln 1 x 1
1
e e 1 1

18. Несобственный интеграл

Замечание.
f x dx не является определенным интегралом.
a
Считается по определению, что
b
f x dx lim f x dx . Если этот предел
a
b a
конечен, то f x dx , называемый
a
несобственным, сходится.
Если же этот предел не является конечным, то
интеграл расходится.

19. Пример

• Вычислить несобственный интеграл
xdx
x2 4
• (или установить его расходимость)
0
0
b
xdx
1
d ( x 2 4) 1
2
lim
lim ln( x 4)
2
2
0
b
x 4 2
x 4
2 b
0
b
1
lim (ln(b 2 4) ln 4)
2 b
• Этот несобственный интеграл
расходится.

20. Пример

Вычислить несобственный интеграл (или
установить
его
расходимость)
dx
0 x 2 4
1
b 1
lim arctg arctg ( )
b 2
2 2
2 2 4
Этот интеграл является сходящимся.

21. Геометрические приложения определенного интеграла

22. Вычисление площадей

Площадь фигуры в
декартовых координатах.
.
Площадь такой
фигуры, называемой
криволинейной
трапецией,
вычисляют по
y f x
y
b
формуле S f x dx .
0
а
b
x
a

23. Вычисление площадей

• Площадь фигуры, ограниченной кривыми
f1 ( x) f 2 ( x)
y1 f1 ( x) и y 2 f 2 ( x ) , (где
) и
x b , находят по
прямыми x aи
формуле:
b
S ( f 2 ( x) f1 ( x)) dx
a

24. Пример

• Найти площадь фигуры, ограниченной линиями
y x2 и y x
2
x
x
Решение:
x4 x
y
y x2
x4 x 0
x x3 1 0
y x
1
0
1
x
1
x 0;
x 0;
x
0
;
x 1.
3
x 1 0.
1
1
2
1
S ( x x )dx x dx x 2 dx
2
0
0
0
2 32 x3 1 2 1 1
( x ) |0 (кв.eд.)
3
3
3 3 3

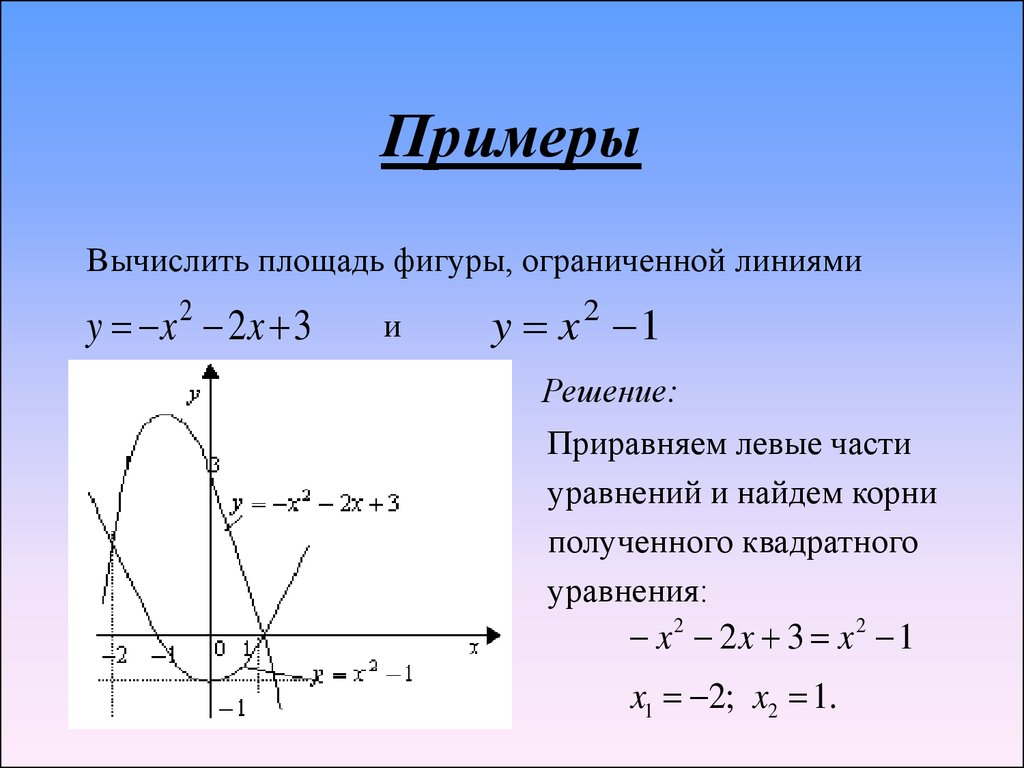
25. Примеры

Вычислить площадь фигуры, ограниченной линиями
y x 2 2x 3
и
y x 2 1
Решение:
Приравняем левые части
уравнений и найдем корни
полученного квадратного
уравнения:
x2 2x 3 x2 1
x1 2; x2 1.

26. Продолжение

Получим S x 2 2 x 3 x 2 1 dx
1
2 x
1
2
2
2
1
2 x 4 dx 2 x 2 x 2 dx
2
x3
x
2
2x
3
2
2
1
2
1 1
8
8 4
1 1
2 2 4 2 2 6
3
3 2
3 2
3 2
1
9
2 3 8 2 9 ( кв.ед.)
2
2

27. ДЯКУЮ ЗА УВАГУ!