Вычисление площади плоской фигуры с помощью определенного интеграла

1.

2. Площади фигур, расположенных над осью Ох

Пусть на отрезке a, b функция f(x) принимает неотрицательные
значения, т.е. f ( x) 0 для любого x a, b . Тогда график функции
y=f(x) расположен над осью Ох.
Если фигура, расположенная над осью Ох, является криволинейной
трапецией( рис 1), то ее площадь вычисляется по известной формуле
b
b
a
a
S f ( x )dx или S ydx
где у находится из уравнения корней.

3.

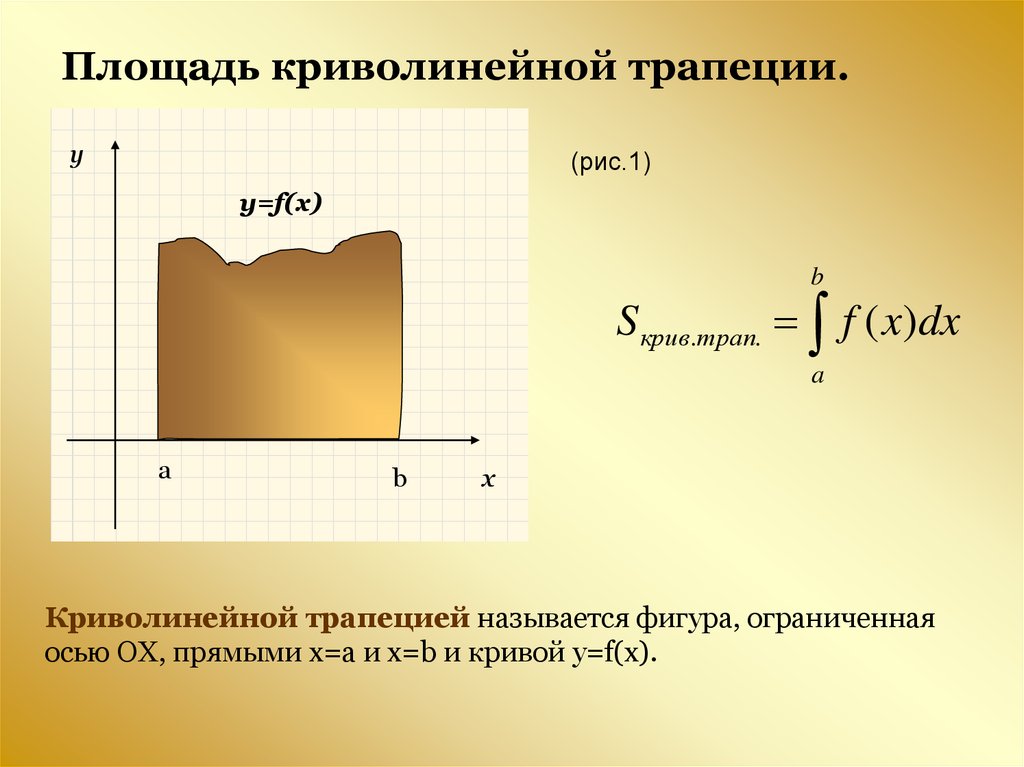
Площадь криволинейной трапеции.
y
(рис.1)
y=f(x)
b
S крив.трап. f ( x)dx
a
a
b
x
Криволинейной трапецией называется фигура, ограниченная
осью ОХ, прямыми х=а и х=b и кривой y=f(x).

4.

Вычислим площади фигур, ограниченных заданными линиями:
• Дано: y 2=9x, x=16, x=25 и y=0
• Решение:
Для любого x 16, 25 функция
y 9 x принимает положительные значения;
поэтому для вычисления площади данной
криволинейной трапеции следует
воспользоваться формулой:
25
S
16
32
x
3
32
25
16
2x x
25
16
25
9 xdx 3 x1 2 dx
16
2(125 64) 2 61 122
(кв.ед)

5.

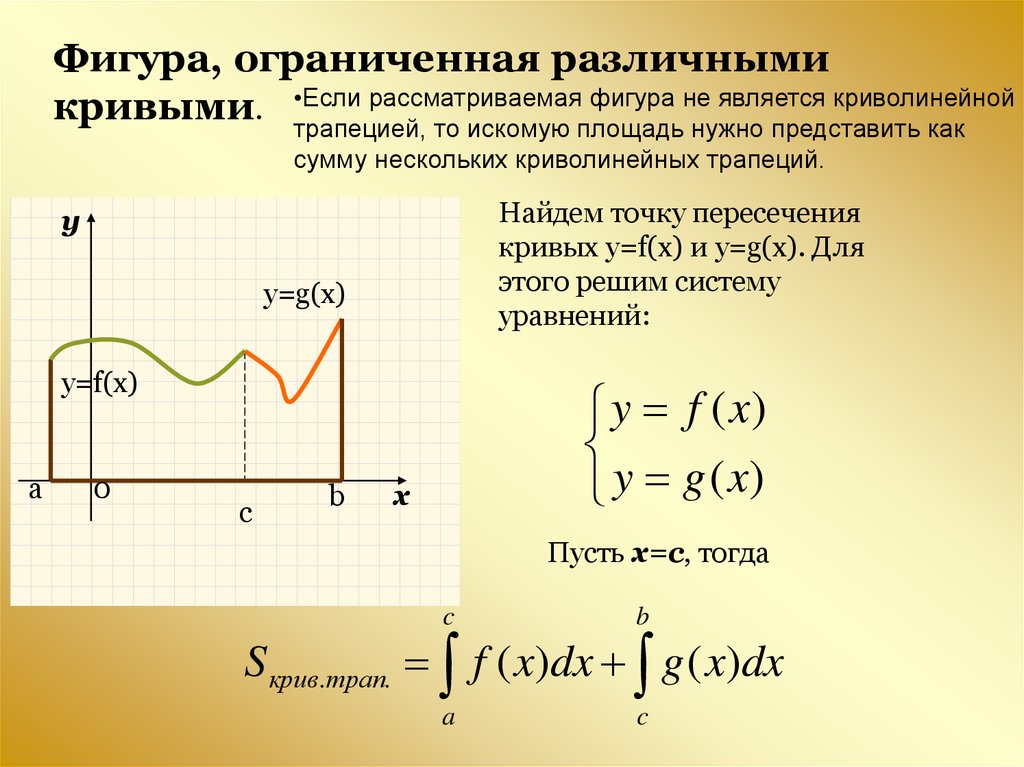
Фигура, ограниченная различными
рассматриваемая фигура не является криволинейной
кривыми. •Если
трапецией, то искомую площадь нужно представить как
сумму нескольких криволинейных трапеций.
Найдем точку пересечения
кривых y=f(x) и y=g(x). Для
этого решим систему
уравнений:
y
y=g(x)
y=f(x)
a
0
c
b
y f ( x)
y g ( x)
x
Пусть x=c, тогда
c
b
a
c
S крив.трап. f ( x)dx g ( x)dx

6.

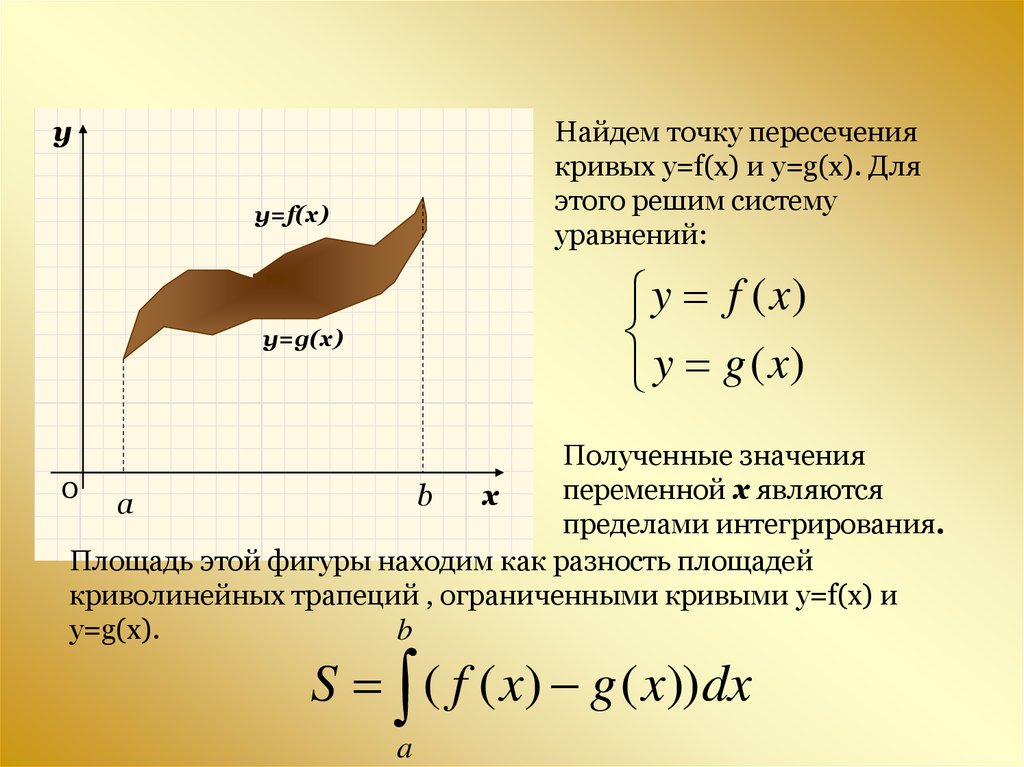
y
Найдем точку пересечения
кривых y=f(x) и y=g(x). Для
этого решим систему
уравнений:
y=f(x)
y f ( x)
y g ( x)
y=g(x)
Полученные значения
0
переменной x являются
b
x
a
пределами интегрирования.
Площадь этой фигуры находим как разность площадей
криволинейных трапеций , ограниченными кривыми y=f(x) и
y=g(x).
b
S ( f ( x) g ( x)) dx
a

7.

• Вычислить площадь фигуры, ограниченной линиями x-2y+4=0, y+x-5=0
и y=0
• Решение: 1. Выполним построение
фигуры. Построим прямую х-2у+4=0;
У=0, х=-47, А(-4, 0); х=0, у=2, В(0, 2).
Построим прямую х+у-5=0; у=0, х=5,
С(5,0); х=0, у=5, D(0,5).
2. Найдем точку пересечения прямых,
для чего решим систему
x 2 y 4 0,
x y 5 0.
Отсюда х=2, у=3,
т.е. М(2;3). Для вычисления искомой площади разобьем треугольник AMC
на два треугольника АМN и NMC, так как при изменении х от N до С –
прямой х+у-5=0.

8.

3. Для треугольника AMN имеем х-2у+4=0; y
1
1
x 2 , f x x 2 ;
2
2
а=-4; b=2. Для треугольника NMC получим х+у-5=0; у=-х+5; f(x)=-х+5;
а=2; b=5.
4. Вычислим площадь каждого из этих треугольников:
x2
1
x 2 dx 2 x
2
4
4
2
S AMN
2
4
9 (кв.ед.).
x2
x 5 dx 5x 52 4,5 (кв.ед.).
2
2
5
S NMC
Следовательно,
Проверка:
S S AMN S NMC 9 4,5 13,5 (кв.ед.).
1
1
S AMC AC NM 9 3 13,5 (кв.ед.).
2
2

9.

2
y
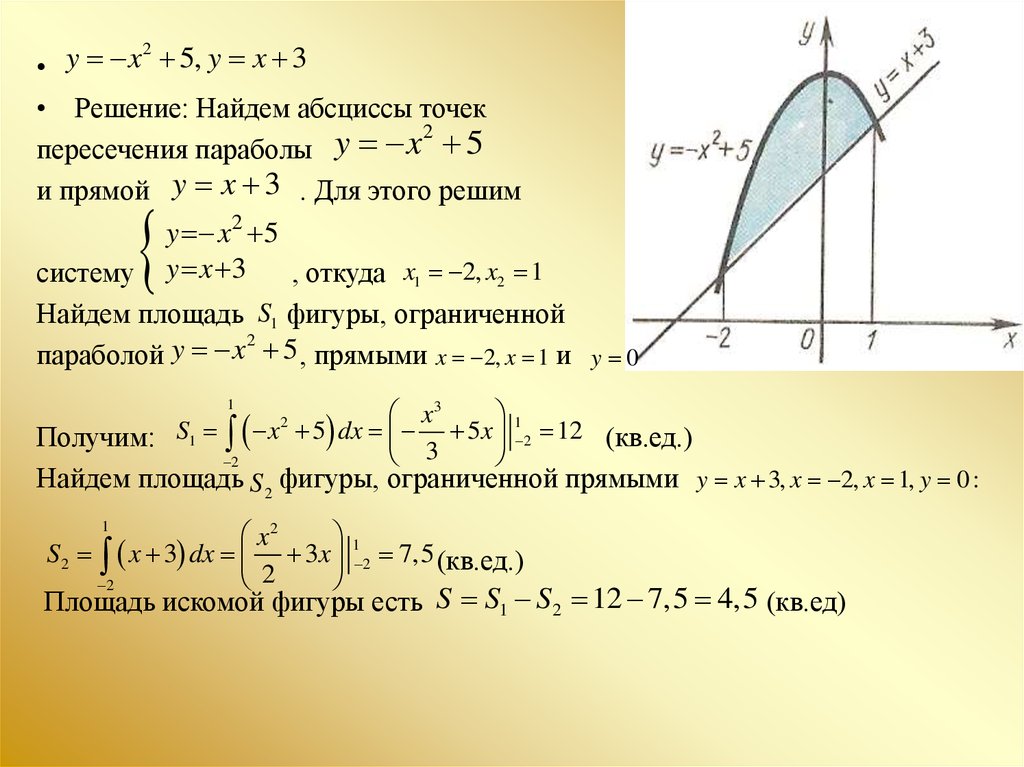
x
5, y x 3
• Решение: Найдем абсциссы точек
2
y
x
5
пересечения параболы
и прямой y x 3 . Для этого решим
y x 2 5
систему y x 3
, откуда x1 2, x2 1
Найдем площадь S1 фигуры, ограниченной
2
y
x
5 , прямыми x 2, x 1 и y 0
параболой
x3
S
x
5
dx
5
x
Получим: 1
3
2
1
2
1
2
12 (кв.ед.)
Найдем площадь S 2 фигуры, ограниченной прямыми y x 3, x 2, x 1, y 0 :
x2
S2 x 3 dx 3x
2
2
1
1
2
7,5 (кв.ед.)
Площадь искомой фигуры есть S S1 S2 12 7,5 4,5 (кв.ед)

10.

• Вычислить площадь фигуры, ограниченной
кривыми y 2 4 x, x 2 4 y
• Решение: Как видно из рисунка, площадь
фигуры ОВАМАО можно представить как
разность площадей фигур ОВМРО и ОАМРО,
где МР – перпендикуляр, опущенный из точки
М на ось Ох.
Найдем координаты точки М. Решив систему уравнений
получим х=4, у=4, т.е. М(4,4).
Следовательно,
4
S
0
4
x2
4 32
4 xdx dx x
4
3
0
3
x
4
0
12
4
0
16 (кв.ед.)
3
y2 4 x
y x2 4

11.

• Данную задачу можно решить и другим способом.
Представим искомую площадь в виде разностей
площадей фигур ОАМNO и OBMNO ( MN –
- перпендикуляр, опущенный из точки М на ось Оу),
т.е. S SOAMNO SOBMNO
Тогда:
4
S
0
4
y2
4 32
4 ydy dy y
4
3
0
3
y
4
0
12
4
0
16
(кв.ед.)
3

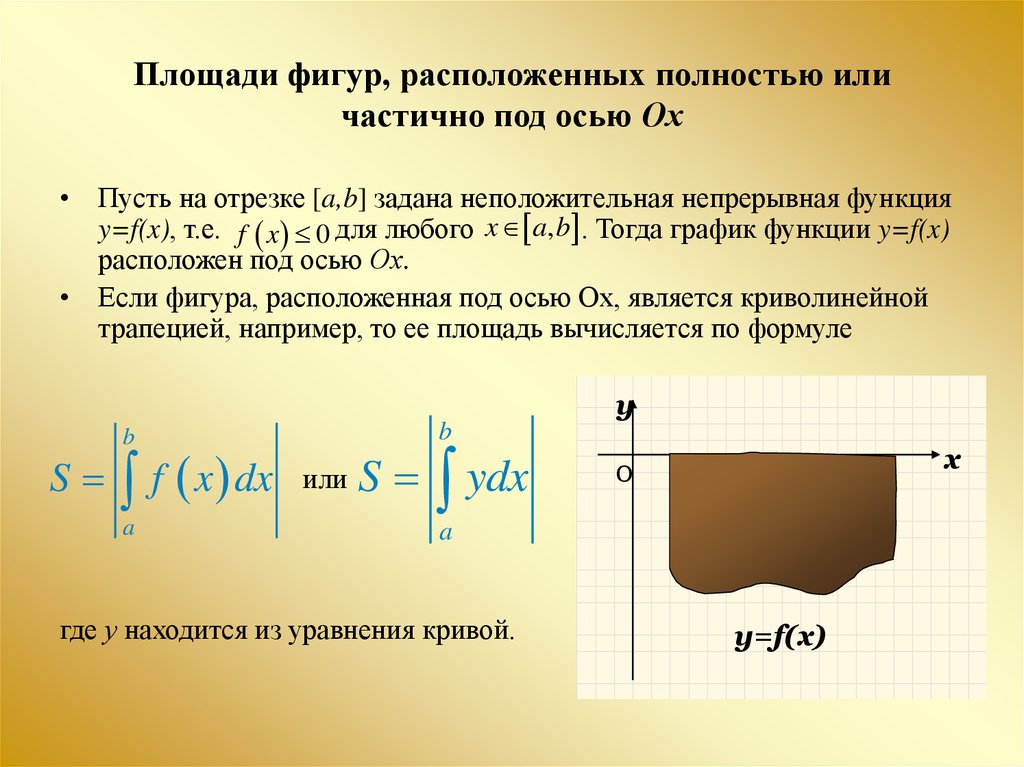
12. Площади фигур, расположенных полностью или частично под осью Ох

• Пусть на отрезке [a,b] задана неположительная непрерывная функция
y=f(x), т.е. f x 0 для любого x a, b . Тогда график функции y=f(x)
расположен под осью Ох.
• Если фигура, расположенная под осью Ох, является криволинейной
трапецией, например, то ее площадь вычисляется по формуле
y
b
b
S
f x dx
a
или
S
ydx
x
0
a
где у находится из уравнения кривой.
y=f(x)

13.

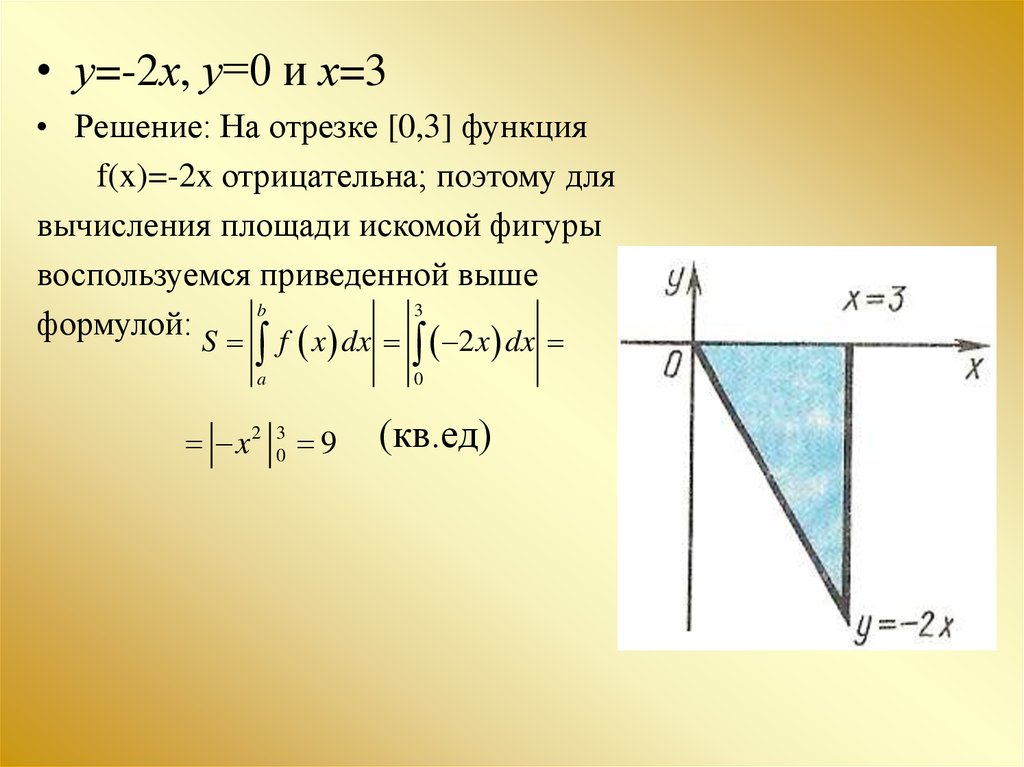
• у=-2х, у=0 и х=3
• Решение: На отрезке [0,3] функция
f(x)=-2x отрицательна; поэтому для
вычисления площади искомой фигуры
воспользуемся приведенной выше
b
3
формулой: S f x dx 2 x dx
a
0
x2
3
0
9
(кв.ед)

14.

• y 4 x x 2 , y 0, x 5.
• Решение: Парабола
пересекает ось абсцисс в точках х=0
и х=4. Фигура, площадь которой требуется
найти, отмечена голубым цветом. Пусть
s1 и S 2 - площади
частей этой фигуры, соответствующих отрезкам
[0,4] и [4,5] а S – искомая площадь; тогда
S S1 S2 .
Используя первую из рассмотренных
формул, получим:
4
2 x3
64 32
(кв.ед.),
S1 4 x x dx 2 x 32
3
3
3
0
4
2
а по второй формуле находим
x
125
64
7
2
2
4
x
x
dx
2
x
50
32
(кв.ед.)
4
3
3
3
4 3
5
S2
5
0
3

15.

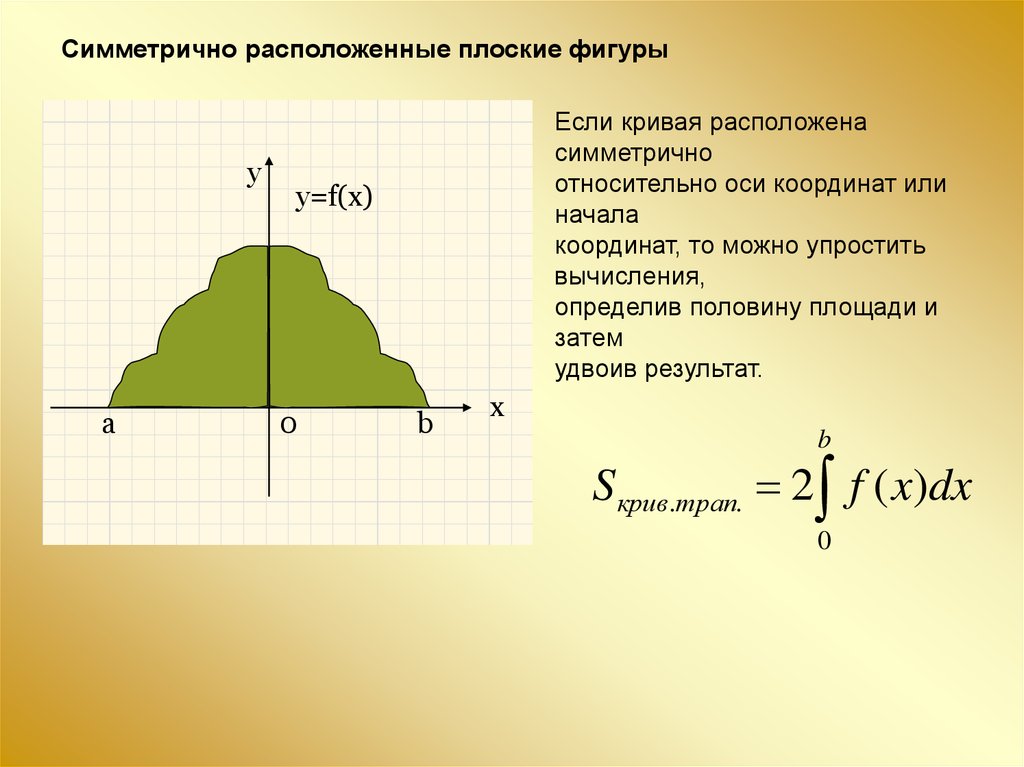
Симметрично расположенные плоские фигуры
y
a
Если кривая расположена
симметрично
относительно оси координат или
начала
координат, то можно упростить
вычисления,
определив половину площади и
затем
удвоив результат.
y=f(x)
0
b
x
b
S крив.трап. 2 f ( x)dx
0

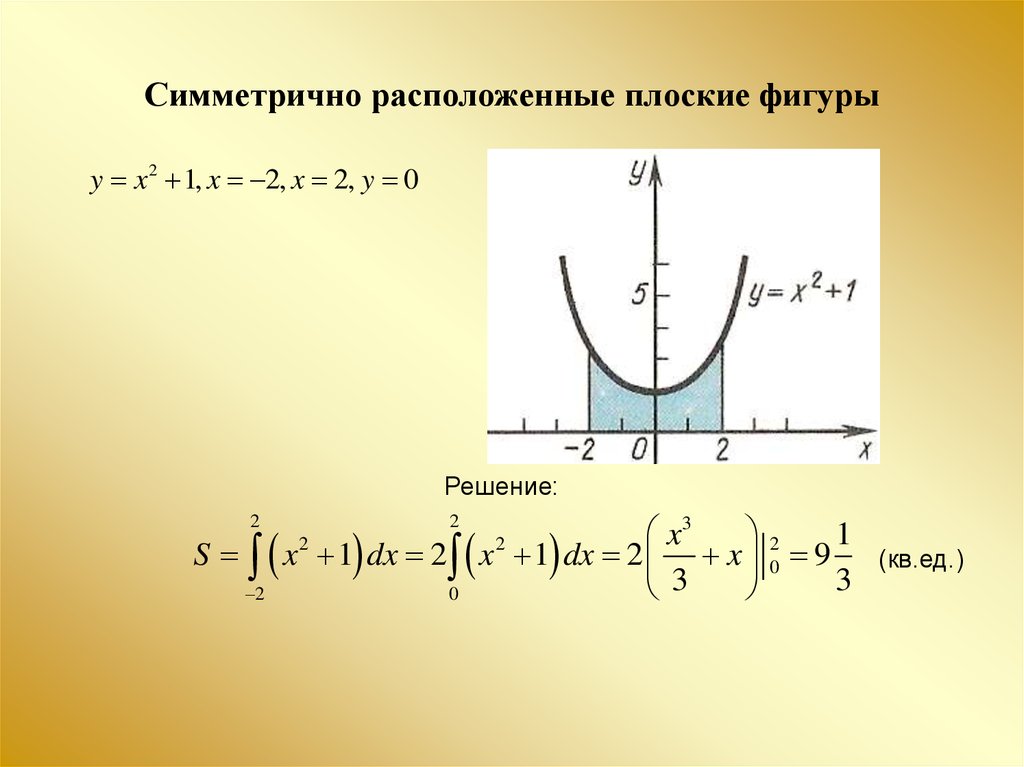
16. Симметрично расположенные плоские фигуры

y x 2 1, x 2, x 2, y 0
Решение:
x3
2
1
S x 1 dx 2 x 1 dx 2 x 0 9
3
3
2
0
2
2
2
2
(кв.ед.)

17.

• Если f(x) на отрезке [a,b] меняет знак
конечное число раз, то этот отрезок
следует разбить на части, на каждой
из которых функция знакопостоянна.
Интеграл по всему отрезку [a,b]
разбивают на сумму интегралов по
полученным частичным отрезкам.
Для вычисления суммы площадей нужно найти сумму абсолютных
величин интегралов по указанным выше отрезкам, т.е. S S1 S2
b
гдеS
c
f x dx, S1 f x dx, S2
a
a
d
b
S3
f x dx , S f x dx
3
c
d

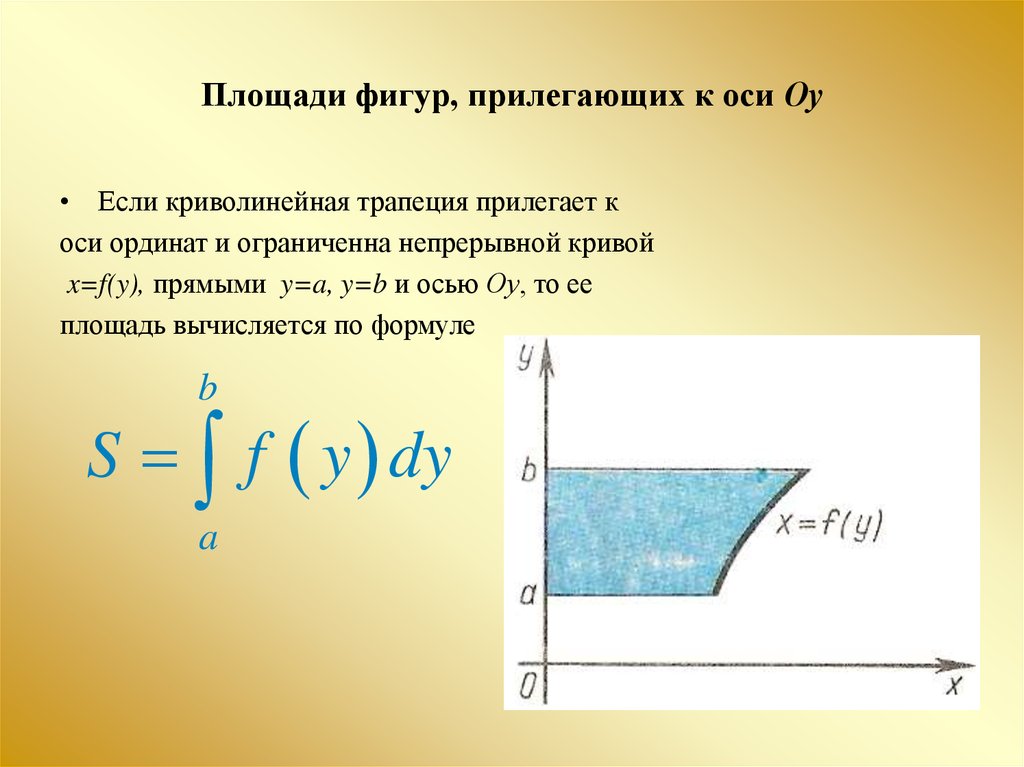
18. Площади фигур, прилегающих к оси Оу

• Если криволинейная трапеция прилегает к
оси ординат и ограниченна непрерывной кривой
x=f(y), прямыми y=a, y=b и осью Оу, то ее
площадь вычисляется по формуле
b
S f y dy
a

19.

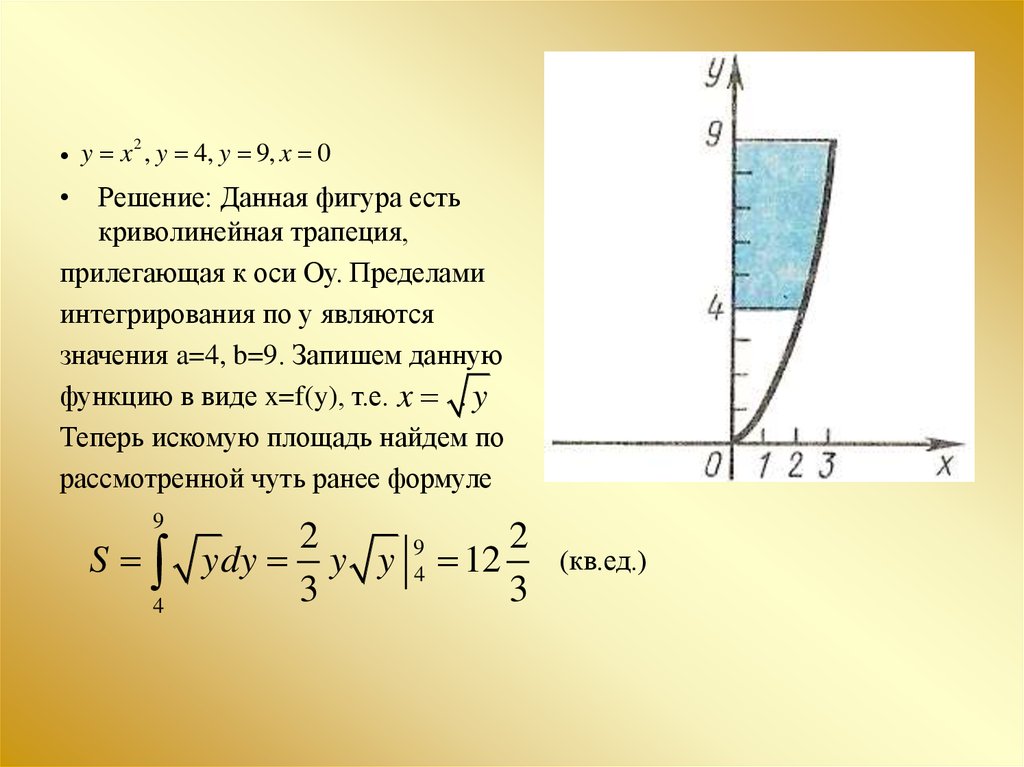
2
• y x , y 4, y 9, x 0
• Решение: Данная фигура есть
криволинейная трапеция,
прилегающая к оси Оу. Пределами
интегрирования по у являются
значения a=4, b=9. Запишем данную
функцию в виде x=f(y), т.е. x . y
Теперь искомую площадь найдем по
рассмотренной чуть ранее формуле
9
S
4
2
ydy y y
3
9
4
2
12
3
(кв.ед.)