Вычисление площадей плоских фигур с помощью определенного интеграла

1. Вычисление площадей плоских фигур с помощью определенного интеграла

2.

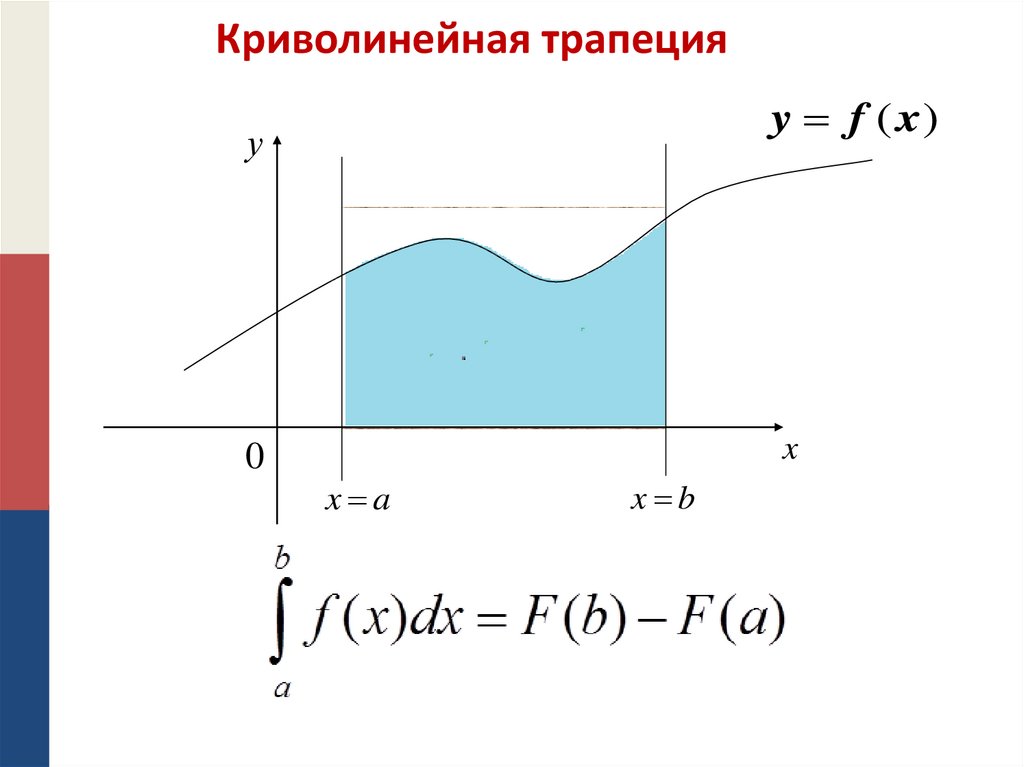
Криволинейная трапеция
y f ( x)
у
0
x
x a
x b

3.

4. Этапы работы

Информация
Оценивание
Контроль
Планирование
Принятие
решения
Выполнение

5. З А Д А Ч А

ЗАДАЧА
Перед зданием школы решено разбить клумбу. Но по
форме клумба не должна быть круглой, квадратной или
прямоугольной. Она должна содержать в себе прямые и
кривые линии. Пусть она будет плоской фигурой,
ограниченной линиями
Y = 4/X + 2; X = 4; Y = 6.
Необходимо ещё подсчитать сколько денег можно
получить за вскапывание этой клумбы, если за каждый м2
выплачивается 50 руб.?

6. Цели урока:

1) самостоятельно спланировать свою работу;
2) научиться составлять алгоритм решения задач на
вычисление площади плоских фигур;
3) уметь аргументировать свою точку зрения;
4) уметь концентрировать внимание на задании;
5) научиться применять определённый интеграл при
решении практических задач;
6) учиться анализировать выполненную работу.

7. Алгоритм последовательности действий при вычислении площади плоской фигуры (Задание 1):

1. По условию задачи сделать схематический чертеж;
2. Представить искомую функцию, как сумму или разность
площадей
криволинейных
соответствующую формулу;
трапеций,
выбрать
3. Найти пределы интегрирования (а и b) из условия
задачи и чертежа t1 и t2, если они не заданы;
4. Вычислить площадь каждой криволинейной трапеции и
площадь искомой фигуры.

8.

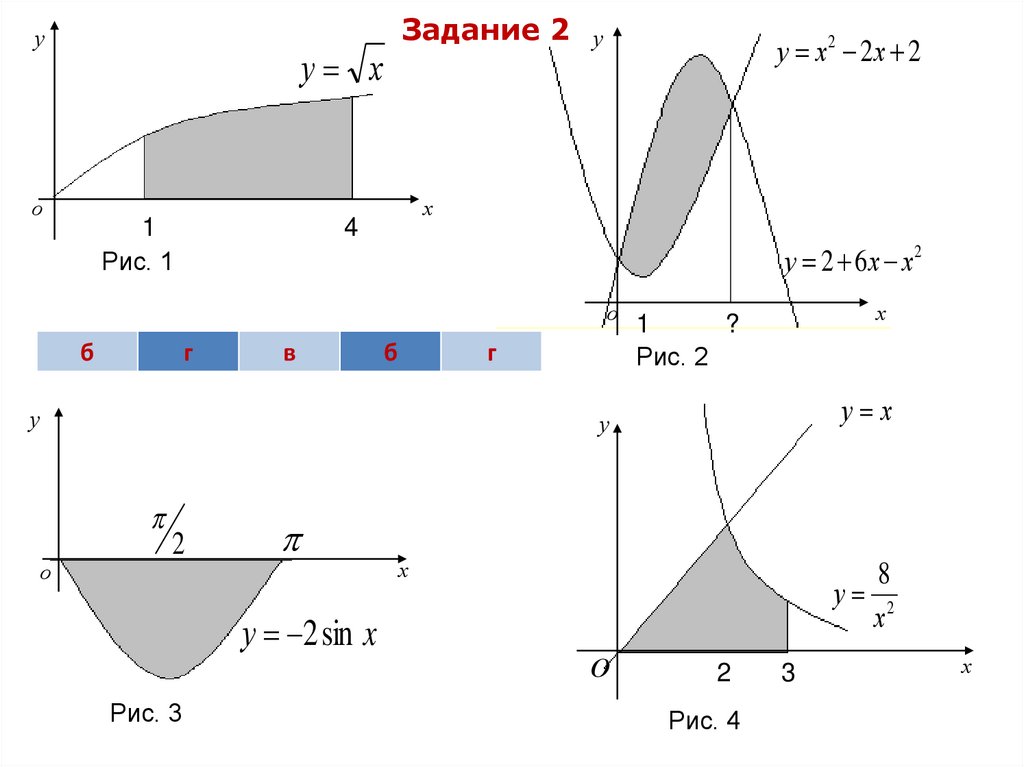
у
Задание 2 у
у х
о
1
Рис. 1
у х2 2х 2
х
4
у 2 6х х2
о
б
г
в
б
г
у
у х
у
о
х
1
?
Рис. 2
2
у 2 sin x
Рис. 3
х
у
о
2
Рис. 4
3
8
х2
х

9. Вычислить площадь земельного участка ограниченного графиком функции:

1)у = 3х2 и прямыми х=1, х=2, у=0.
2) у= 2х, прямыми х=2, х=3 и отрезком оси Ох от 2 до 3.
3) у=х3 прямыми х=1 х=3 и отрезком оси Ох от 1 до 3.
4) Вычислите площадь фигуры, ограниченной линиями
y = –x2 + 9, у=0.
5) Вычислите площадь фигуры, ограниченной линиями:
у= х2 и у= -х+2.

10. Ответы к задачам (Задание 3)

Вариант 1
7
кв. ед
Вариант 2
5
кв. ед.
Вариант 3
4 кв. ед.
Вариант 4
36
кв. ед.
Вариант 5
4,5
кв. ед.

11.

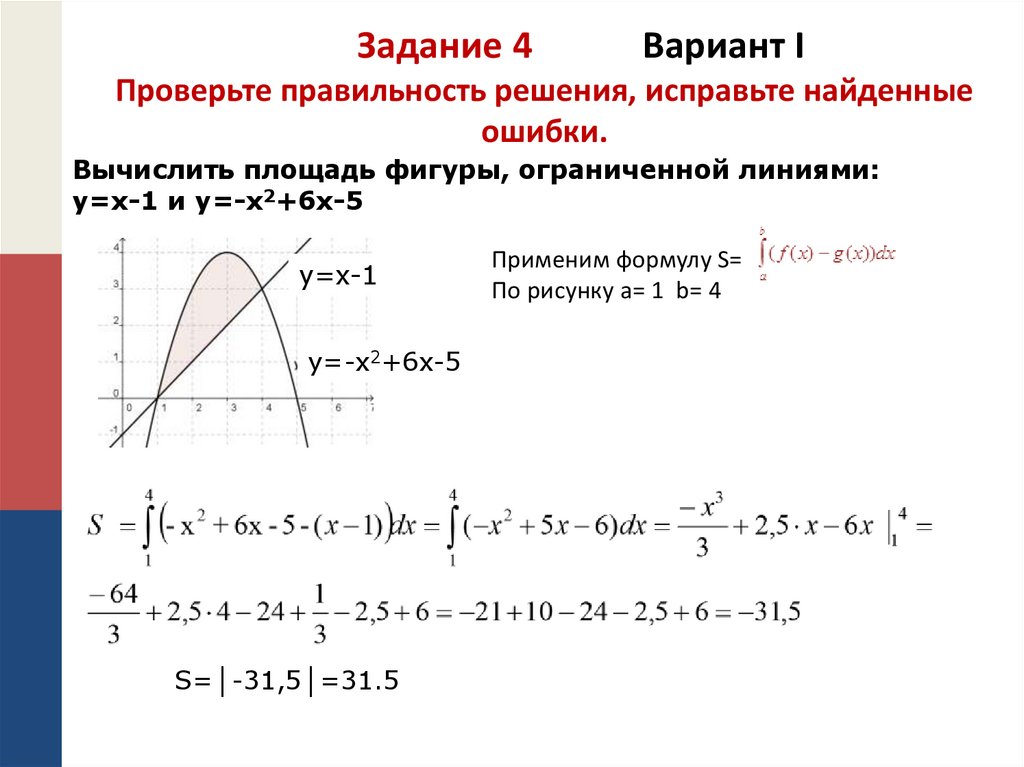
Задание 4
Вариант I
Проверьте правильность решения, исправьте найденные
ошибки.
Вычислить площадь фигуры, ограниченной линиями:
y=x-1 и y=-x2+6x-5
y=x-1
y=-x2+6x-5
S=│-31,5│=31.5
Применим формулу S=
По рисунку а= 1 b= 4

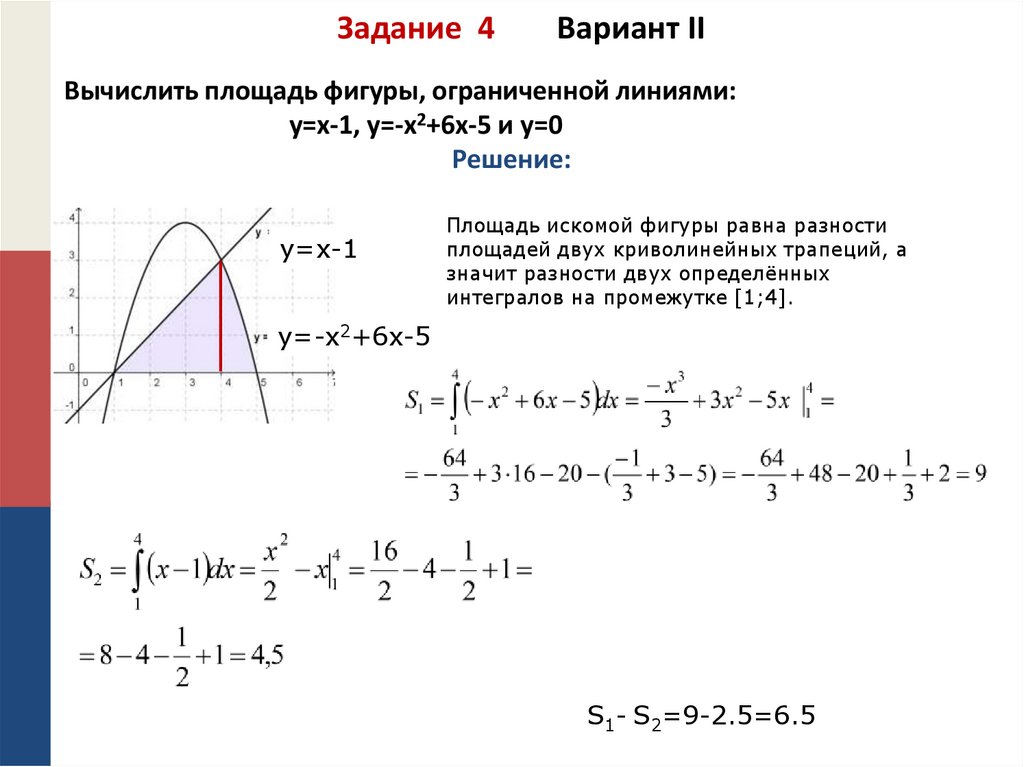
12. Задание 4 Вариант II

Вычислить площадь фигуры, ограниченной линиями:
y=x-1, y=-x2+6x-5 и у=0
Решение:
y=x-1
Площадь искомой фигуры равна разности
площадей двух криволинейных трапеций, а
значит разности двух определённых
интегралов на промежутке [1;4].
y=-x2+6x-5
S1- S2=9-2.5=6.5

13.

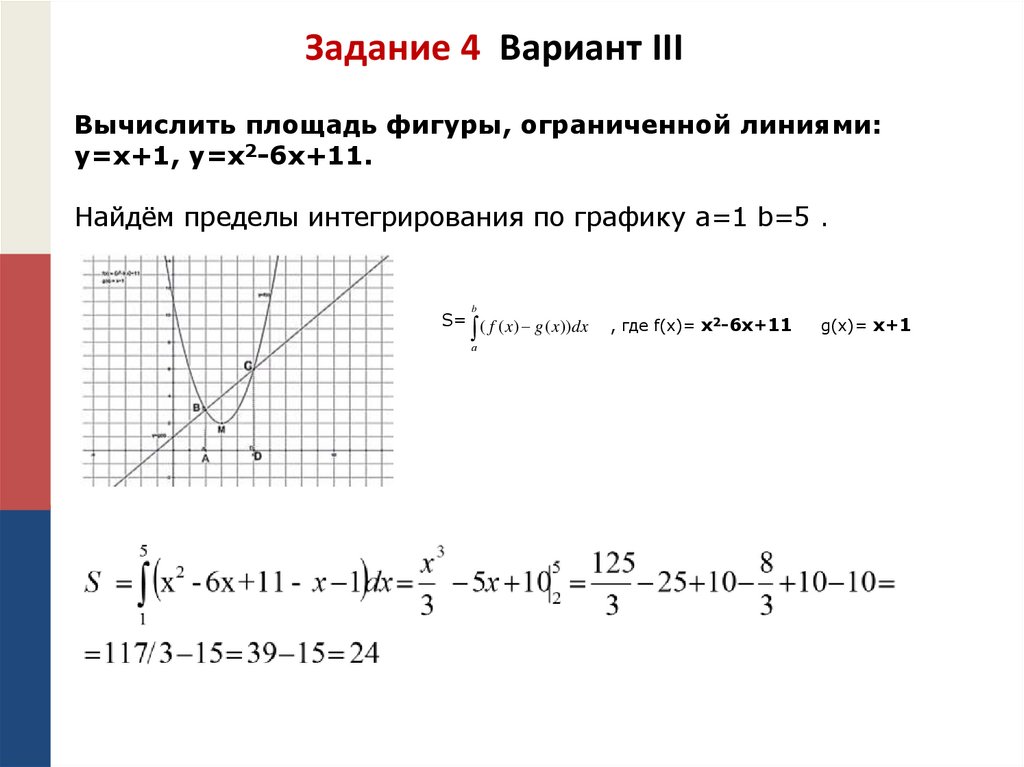
Задание 4 Вариант III
Вычислить площадь фигуры, ограниченной линиями:
y=x+1, y=x2-6x+11.
Найдём пределы интегрирования по графику a=1 b=5 .
b
S= ( f ( x) g ( x)) dx
а
, где f(x)= x2-6x+11
g(x)= x+1

14. З А Д А Ч А

ЗАДАЧА
Перед зданием школы решено разбить клумбу. Но по
форме клумба не должна быть круглой, квадратной или
прямоугольной. Она должна содержать в себе прямые и
кривые линии. Пусть она будет плоской фигурой,
ограниченной линиями
Y = 4/X + 2; X = 4; Y = 6.
Необходимо ещё подсчитать сколько денег можно
получить за вскапывание этой клумбы, если за каждый м2
выплачивается 50 руб.?

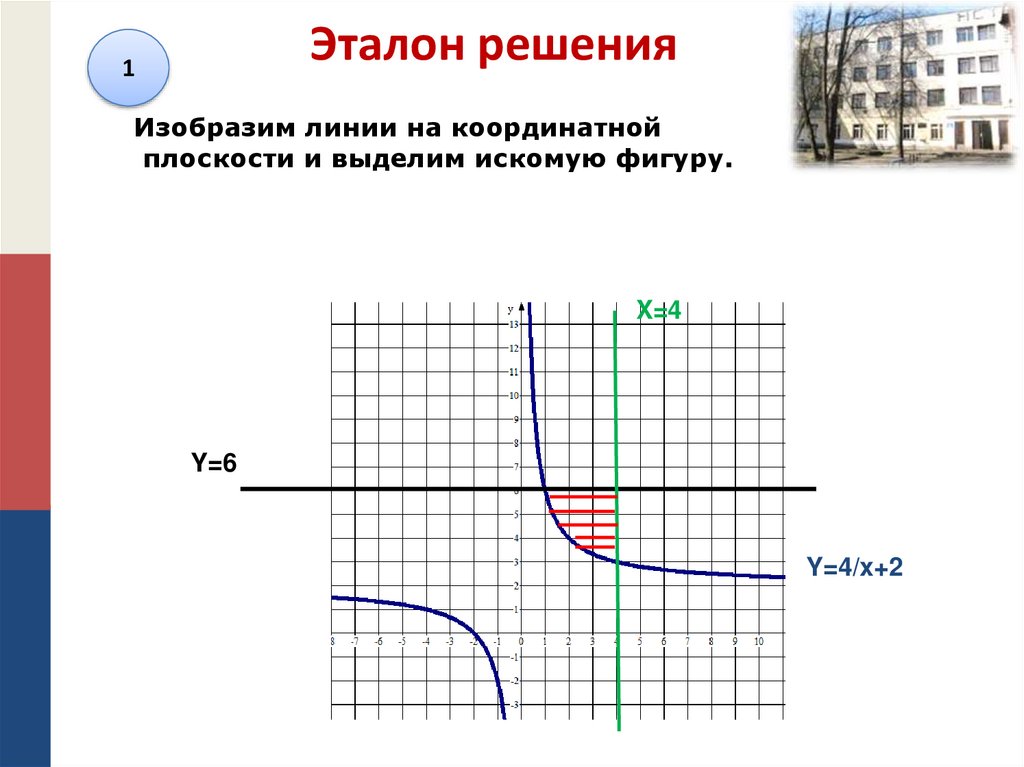
15. Эталон решения

1
Изобразим линии на координатной
плоскости и выделим искомую фигуру.
X=4
Y=6
Y=4/x+2

16. Эталон решения

2
Эталон решения
Вычислим площадь полученной фигуры по
формуле:
где f(x)= 6, а g(x)=4/x +2

17. Эталон решения

Найдем пределы интегрирования:
Х = 4 – по условию, следовательно,
абсцисса точки пересечения графиков
Y = 4/X + 4 и Y = 6.
Решим уравнение 4/X + 2 = 6;
4/X = 4
X = 1.

18. Эталон решения

4
Эталон решения
Так как за каждый квадратный метр
выплачивается 50 рублей, то заработок составит:
6,4 * 50 = 320 (рублей).

19.

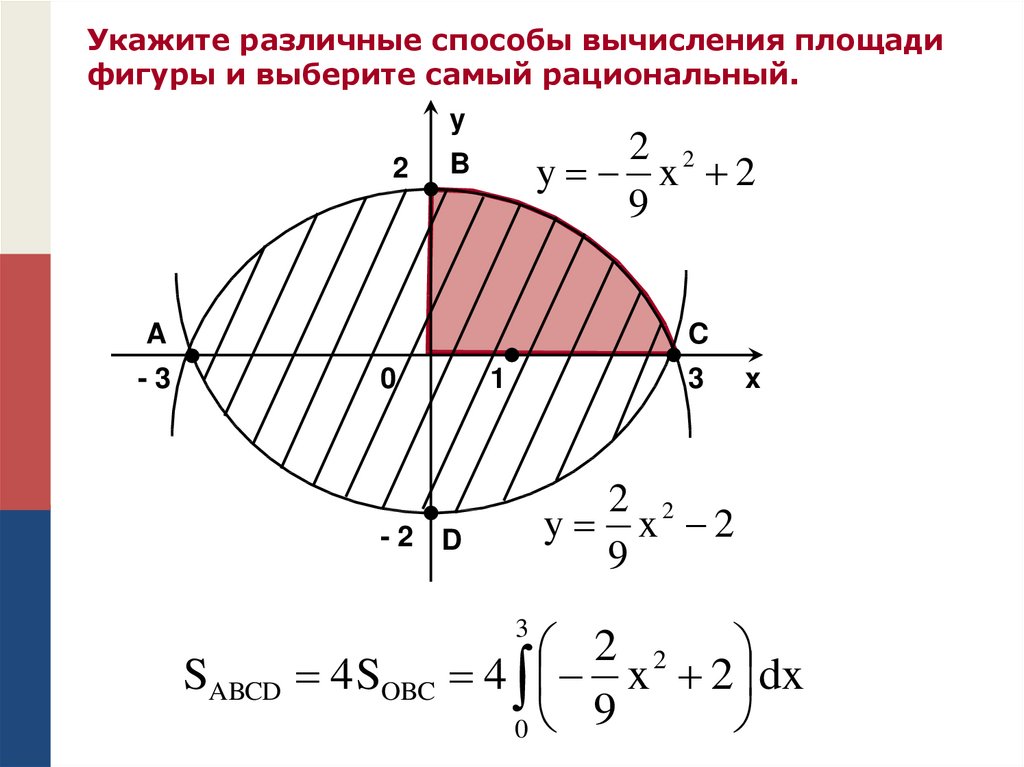
Укажите различные способы вычисления площади
фигуры и выберите самый рациональный.
y
2
2 2
y x 2
9
B
A
-3
C
0
1
3
2 2
y x 2
9
-2 D
2 2
4 x 2 dx
9
0
3
SABCD 4 SOBC
x

20. Цели урока:

1) самостоятельно спланировать свою работу;
2) научиться составлять алгоритм решения задач на
вычисление площади плоских фигур;
3) уметь аргументировать свою точку зрения;
4) уметь концентрировать внимание на задании;
5) научиться применять определённый интеграл при
решении конкретных задач;
6) учиться анализировать выполненную работу.