Обратные тригонометрические функции. Схема обратных тригонометрических функций

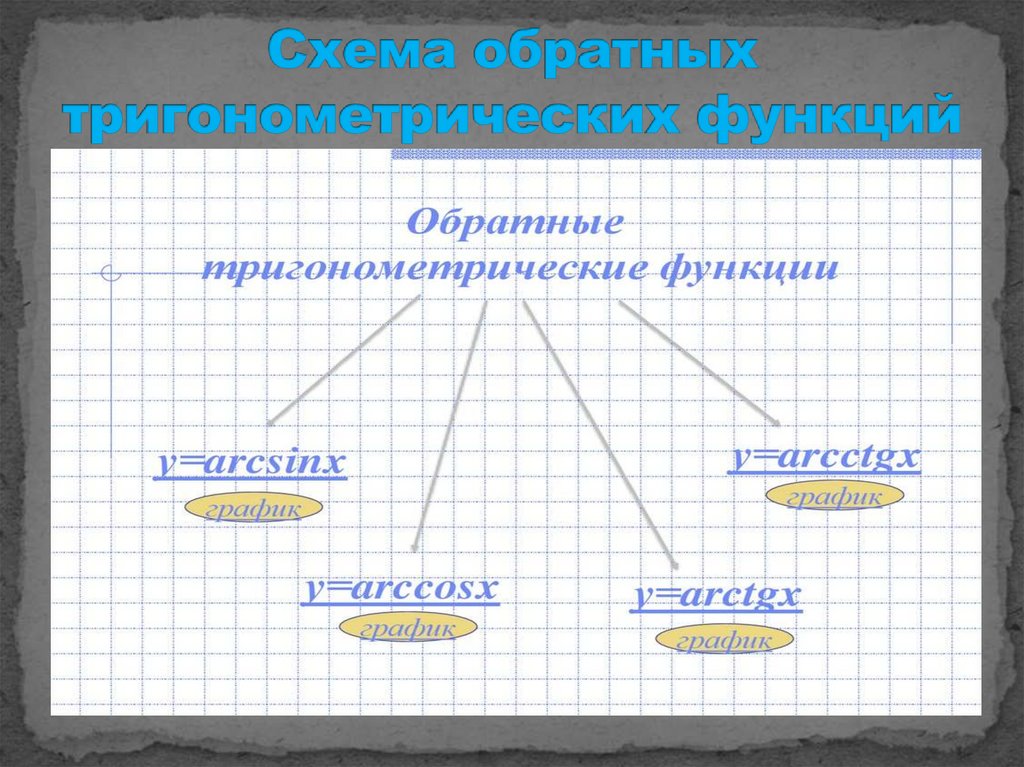
1. Обратные тригонометрические функции

12.02.2024

2. Схема обратных тригонометрических функций

3.

4.

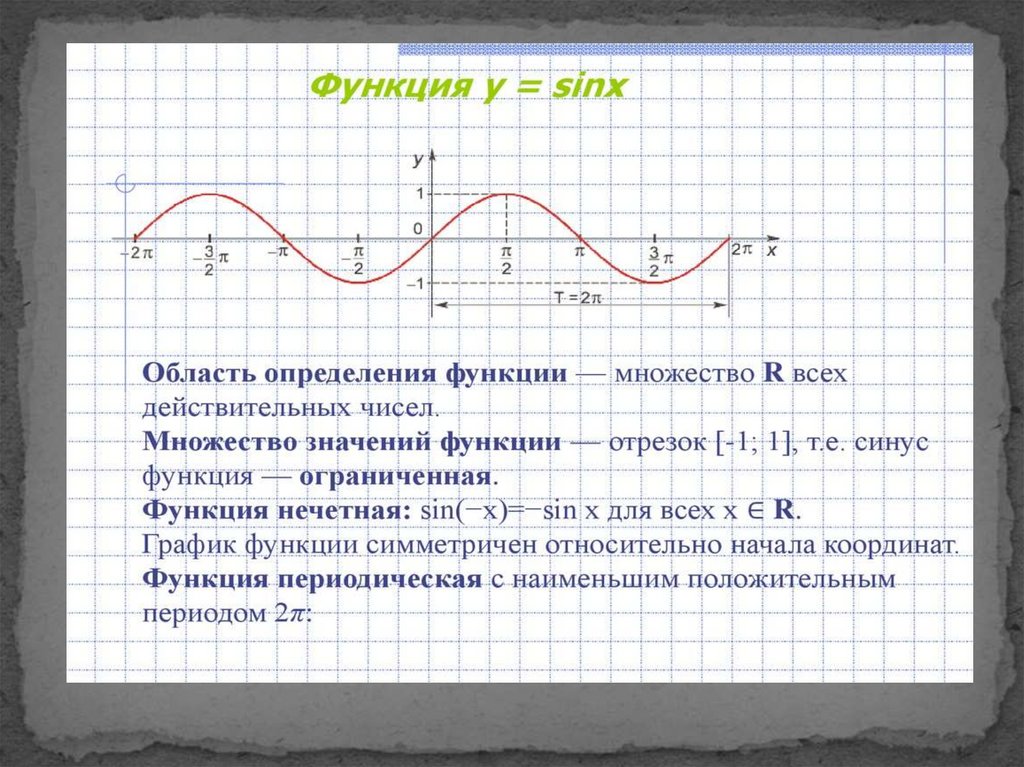
Функция у = sin x

5.

6.

7.

8.

9.

10.

11.

12. Тригонометрические операции над обратными тригонометрическими функциями

арксинус
арккосинус
арктангенс
арккотангенс
[-1;1] → [-π/2;π/2]
[-1;1] → [0;π]
R → (-π/2;π/2)
R → (0;π)
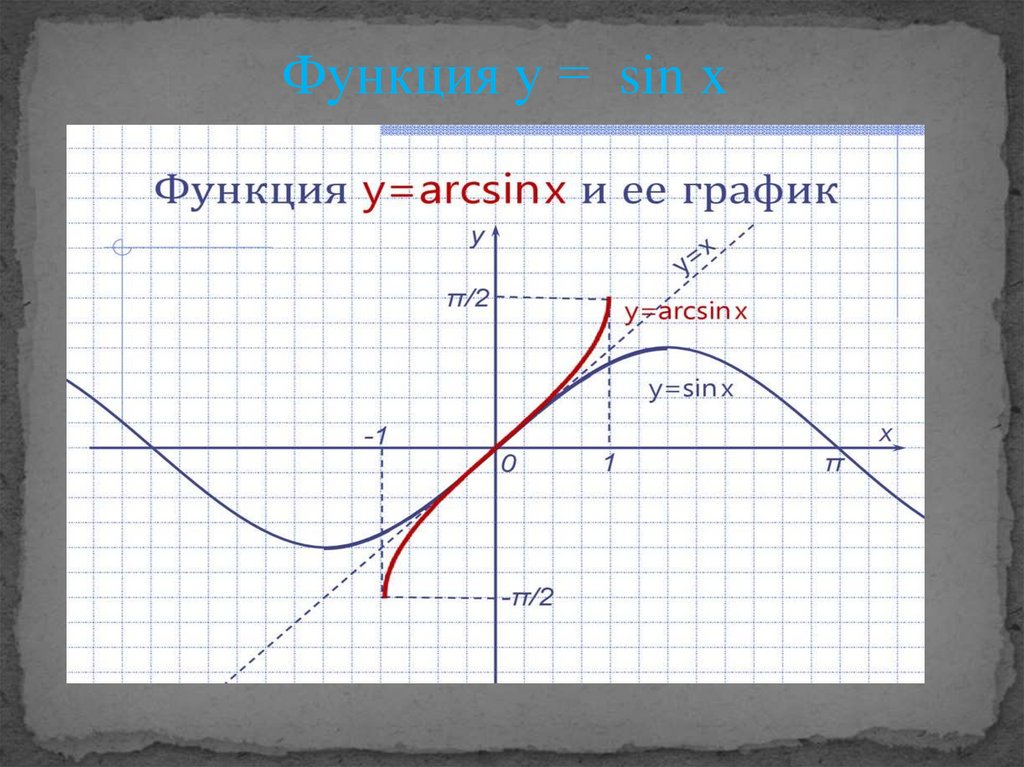
x → arcsinx
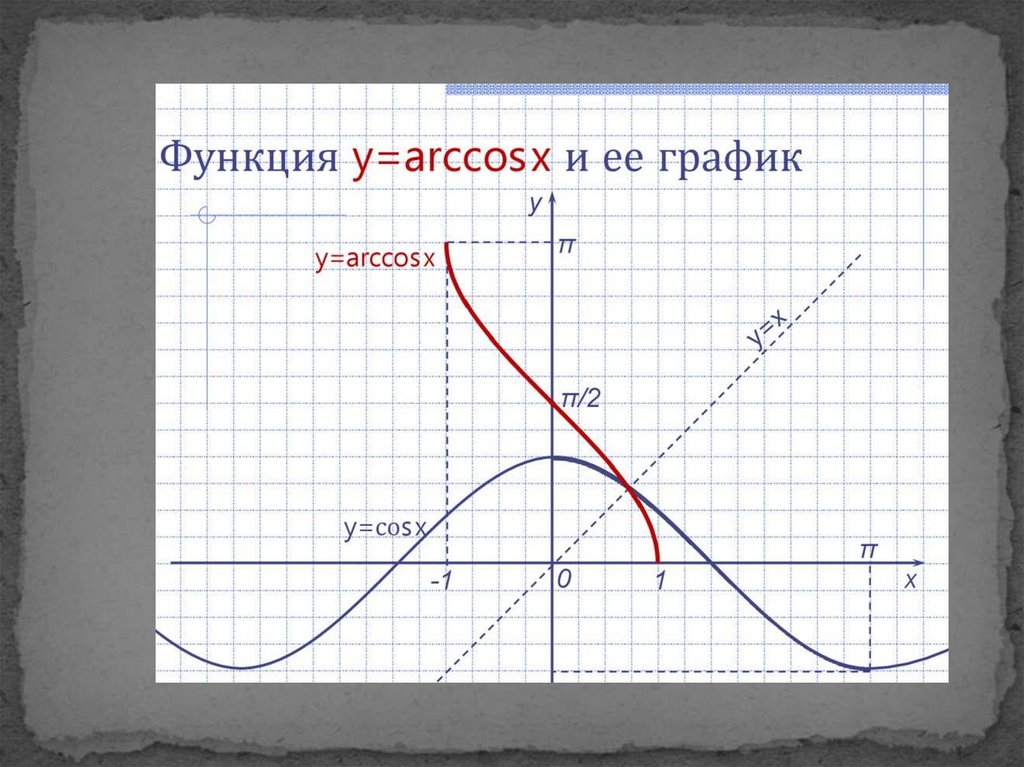
x → arccosx
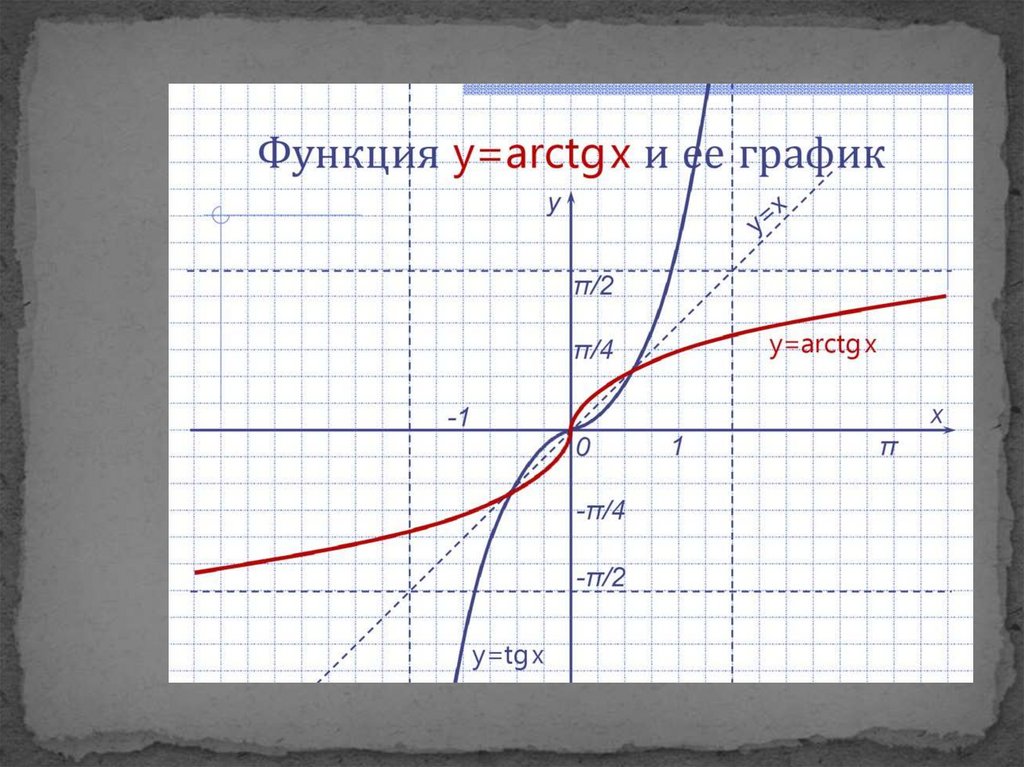
x → arctgx
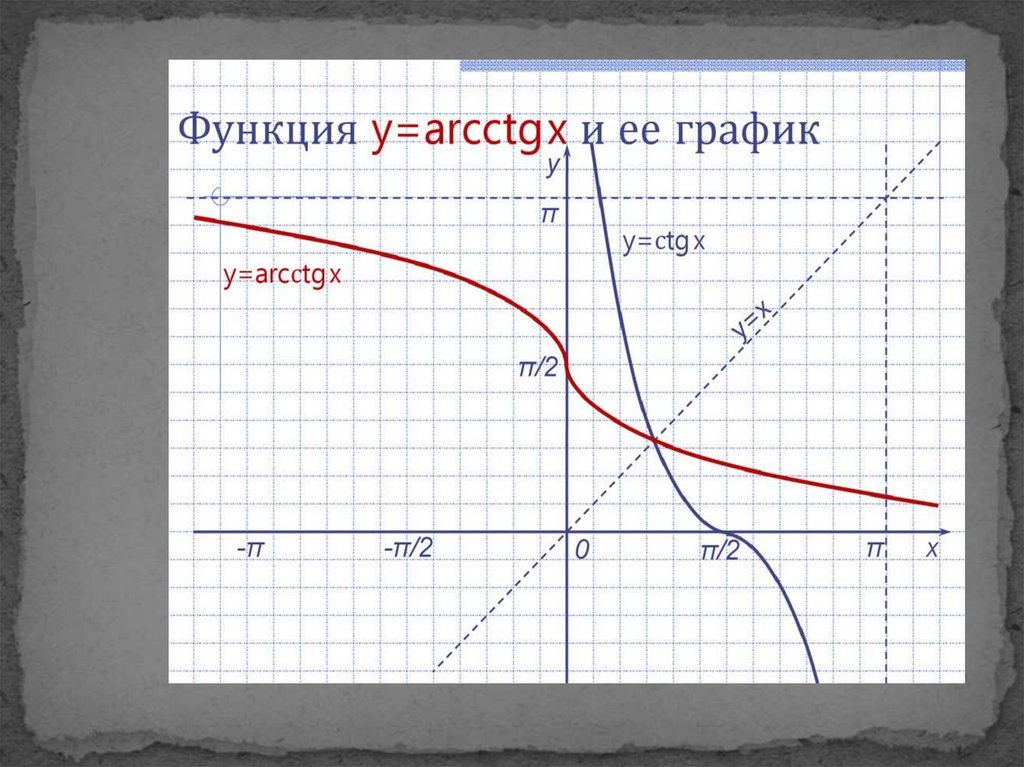
x → arcctgx
1) D (arcsinx) = [-1;1].
1) D (arccosx) =[-1;1].
1) D (arctgx) = R.
1) D (arcctgx) = [-1;1].
2) E (arcsinx) = [π/2;π/2].
2) E (arccosx) = [0;π].
2) E (arctgx) = (-π/2;π/2).
2) E (arcctgx) = (0;π).
3) arcsinx = 0 при х = 0.
3) arccosx = 0 при х = 1.
3) arctgx = 0 при х = 0.
3) arcctgx 0 при любом х R.
4) arcsinx > 0 при 0 < x ≤ 1.
аrcsinx < 0 при -1 ≤ x < 0.
4) arccosx > 0 при -1 ≤ x ≤ 1.
4) arctgx > 0 при x >0
arctgx < 0 при x < 0.
4) arcctgx > 0 при любом х R.
5) Нечетная, так как
arcsin(-x) = - arcsinx.
5) Функция общего вида.
5) Нечетная, так как arctg(-x)
= -arctgx.
5) Функция общего вида.
6) Непрерывна на всей области
определения.
6) Непрерывна на всей области
определения.
6) Непрерывна на всей области
определения.
6) Непрерывна на всей области
определения.
7) Возрастает на всей области
определения.
7) Убывает на всей области
определения.
7) Возрастает на всей области
определения.
7) Убывает на всей области
определения.
8) yнаиб = π/2 при х = 1.
yнаим = -π/2 при х = -1.
8) yнаиб = π при х = -1.
yнаим = 0 при х = 0.
8) Нет
8) Нет.
9) Асимптот нет.
9) Асимптот нет.
9) y = π/2.
y = -π/2.
9) y=π.
y=0.