Теория информации. Энтропия и информация

1.

Теория информации
Кабанов Александр Николаевич
к.ф.-м.н., доцент кафедры кибернетики

2.

1. Энтропия и информация
2

3.

Вероятностная схема
• Пусть A = {a1, a2, …, an, …} – полная группа попарно несовместных
событий (исходов), pi = p(ai) – вероятность события ai.
a
a
1 a
2 ...
n ...
pi 1
• Тогда A
–
вероятностная
схема,
i
p
p
...
p
...
n
1 2
3

4.

Дискретная вероятностная схема
• Если множество A не более чем счётно, то вероятностная схема A
называется дискретной.
• Иначе вероятностная схема A называется непрерывной.
• В этом случае вероятностное распределение на исходах задаётся
с помощью плотности распределения вероятности p(x).
• Если множество A конечно, то и схема называется конечной.
• В дальнейшем будем рассматривать конечные вероятностные
схемы.
4

5.

Количество информации по Хартли
1. Пусть сообщение T1, записанное в алфавите A1, |A1| = n1, имеет
длину l1, а сообщение T2, записанное в алфавите A2, |A2| = n2,
имеет длину l2. Тогда сообщения T1 и T2 несут одинаковое
количество информации, если n1l1 = n2l2.
2. Количество информации, содержащееся в сообщении,
пропорционально его длине.
• Количество информации в сообщении длины l, записанном в
алфавите A мощностью n:
I = log2nl
5

6.

Количество информации по Шеннону
1. Пустое сообщение не содержит информации.
2. Количество информации, содержащееся в сообщении,
пропорционально его длине.
• Пусть символы алфавита A = {a1, a2, …, an} появляются в
сообщениях с вероятностями p1, p2, …, pn.
• Количество информации в сообщении длины l, записанном в
алфавите A:
n
I
l
p
p
ilog
2
i
1
i
6

7.

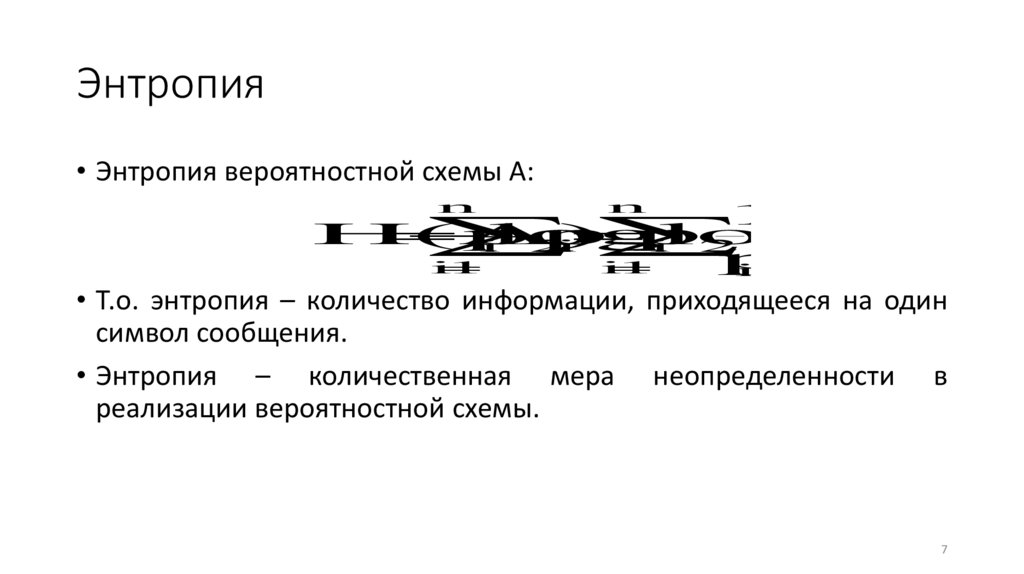
Энтропия
• Энтропия вероятностной схемы A:
n
n
1
H(A)
p
log
p
p
log
i
2
i
i
2
p
i
1
i
1
i
• Т.о. энтропия – количество информации, приходящееся на один
символ сообщения.
• Энтропия – количественная мера неопределенности в
реализации вероятностной схемы.
7

8.

Единицы измерения
• Основание логарифма определяет единицу измерения
количества информации.
• Если основание логарифма 2, то информацию измеряют в
двоичных единицах – битах.
• Если основание логарифма 10, то информацию измеряют в
десятичных единицах – дитах.
• Если основание логарифма e, то информацию измеряют в
натуральных единицах – натах.
8

9.

Аксиомы Хинчина
• Энтропия конечной вероятностной схемы с точностью до
постоянного множителя однозначно определяется системой
аксиом:
n
1.H(p1,…,pn) – ненулевая непрерывная функция, 0 ≤ pi ≤ 1, pi 1.
i 1
2.H(p1,…,pn) симметрична по переменным.
3.H(p1,…,pn,0) = H(p1,…,pn).
n
q
q
i1
im
p
,
4. H(q11,…,q1m,q21,…,q2m,…,qn1,…,qnm) = H(p1,…,pn) +
iH
p,...,
p
i
1
i
i
где pi = qi1 + … + qim.
1 1
5. H(p
,...,
p
)
H
.
,...,
1
n
n n
9

10.

Аксиомы Фадеева
• Система аксиом Фадеева эквивалентна системе аксиом Хинчина:
1.H(p,1–p) – непрерывная и положительная хотя бы в одной точке
функция, 0 ≤ pi ≤ 1,
2.H(p1,…,pn) симметрична по переменным.
q1 q2
,
3.При n ≥ 2 H(p1,…,pn-1,q1,q2) = H(p1,…,pn) + pnH
p p ,
n n
где pn = q1 + … + q2.
10

11.

Минимальная энтропия
• Докажем, что H(1,0) = 0 из аксиом Хинчина.
• По аксиоме Х3: H(½,½,0,0) = H(½,½).
• По аксиоме Х2: H(½,½,0,0) = H(½,0,½,0).
• По аксиоме Х4: H(½,0,½,0) = H(½,½) + ½H(1,0) + ½H(1,0) = H(½,½) +
H(1,0).
• Следовательно, H(½,½) = H(½,½) + H(1,0).
• Значит, H(1,0) = 0.
11

12.

Минимальная энтропия
• Докажем, что H(1,0) = 0 из аксиом Фадеева.
• По аксиоме Ф2: H(½,½,0) = H(0,½,½).
• По аксиоме Ф3: H(0,½,½) = H(0,1)+1·H(½,½) = H(1,0)+H(½,½).
• По аксиоме Ф3: H(½,½,0) = H(½,½) + ½H(1,0).
• Следовательно, H(1,0)+H(½,½) = H(½,½) + ½H(1,0).
• Значит, H(1,0) = ½H(1,0).
• Значит, ½H(1,0) = 0.
• Значит, H(1,0) = 0.
12

13.

Объединённая вероятностная схема
n
a
...
a
1
n
• Рассмотрим вероятностные схемы A
,
p
i,и
p
p
i
1
1 ...
n
m
b
...
b
1
m
B
,
q
.
j
q
q
1
1 ...
m
j
• Вероятностная схема
a
b
...
a
b
a
b
...
a
b
...
a
b
1
1
1
m
2
1
2
m
n
m
С
AB
p
...
p
p
...
p
...
p
111m
21 2m
nm
называется объединённой вероятностной схемой.
13

14.

Объединённая вероятностная схема
• Для вероятностей pij выполняются следующие соотношения:
nm
n
m
ij
i
1
j
1
ij j
i
1
ij i
j
1
p
1,
p
q
,
p
p
.
• Энтропией объединённой вероятностной схемы AB называется
величина
nm
H(AB)
p
log
p
ij
2
ij
i
1j
1
14

15.

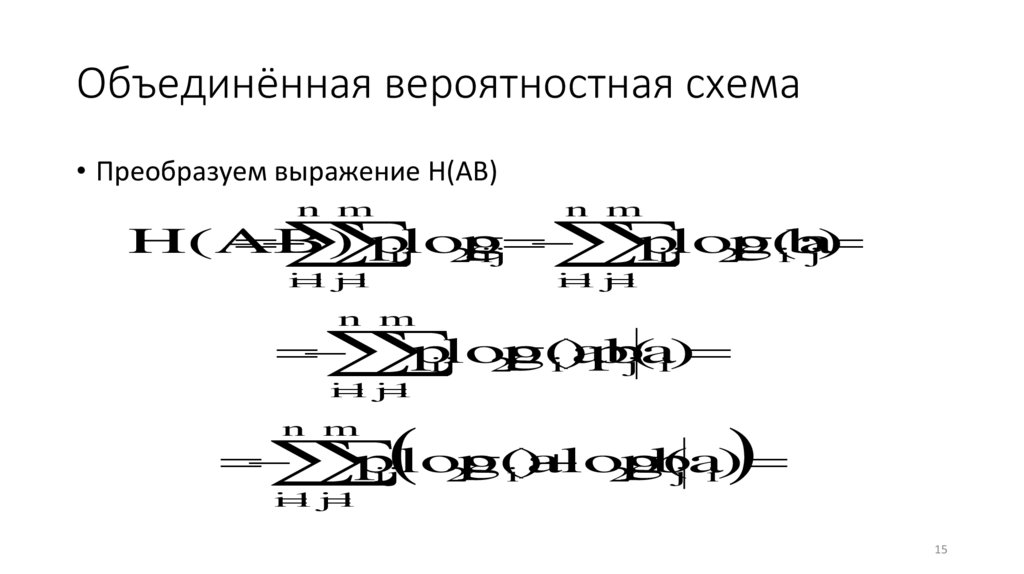
Объединённая вероятностная схема
• Преобразуем выражение H(AB)
n m
n m
i
1 j
1
i
1 j
1
H(AB)
p
log
p
p
log
p(a
ij
2
ij
ij
2
ib
j)
n m
p
log
p(a
b
ij
2
i)p(
ja
i)
i
1 j
1
n m
p
p(a
log
p(
b
ijlog
2
i)
2
ja
i)
i
1 j
1
15

16.

Объединённая вероятностная схема
n m
n m
i
1j
1
i
1j
1
p
log
p(a
p
log
p(
b
ij
2
i)
ij
2
ja
i)
n
n m
i
1
i
1j
1
p
p
p
log
p(
b
ilog
2
i
ij
2
ja
i)
nm
H(A)
p
log
p(
b
)
ij
2
ja
i
i
1
j1
16

17.

Условная энтропия
nm
H(B
|A)
p
log
p(
b
)
ij
2
ja
i
i
1
j1
• Эта величина называется условной энтропией вероятностной
схемы B относительно вероятностной схемы A.
• Т.о. H(AB) = H(A) + H(B|A).
• Аналогично, H(AB) = H(B) + H(A|B).
nm
H(A
|B)
p
log
p(a
)
ij
2
ib
j
i
1
j1
17

18.

Условная энтропия
m
H(B
|
a
)
p(
b
a
)log
p(
b
a
)
i
j
i
2
j
i
j
1
• Эта величина называется условной энтропией вероятностной
схемы B относительно исхода ai.
• Имеет место следующее соотношение:
n m
H(B
|A)
p
log
p(
b
ij
2
ja
i)
i
1 j
1
n m
p(a
b
p(
b
i)p(
ja
i)log
2
ja
i)
i
1 j
1
18

19.

Условная энтропия
m
p(a
p(
b
a
)log
p(
b
a
)
i)
j
i
2
j
i
i
1
1
j
n
n
p
|a
iH(B
i)
i
1
• Поэтому H(B|A) называют средней условной энтропией.
19

20.

Условная энтропия
• Пусть A и B – независимые вероятностные схемы. Тогда:
nm
H(B
|A)
p
log
p(
b
a
)
ij
2
j
i
i
1
j
1
n
m
n m
i
1
j
1
i
1j
1
p
q
log
q
p
q
log
q
i
j
2
j
i
j
2
j
m
q
log
q
H(B)
j
2
j
j
1
20

21.

Энтропия объединённой и составляющих
схем
• Теорема: Для любых двух конечных вероятностных схем
справедливо неравенство:
H(AB) ≤ H(A) + H(B).
Равенство имеет место тогда и только тогда, когда схемы A и B
независимы.
• Следствие 1: H(B|A) ≤ H(B).
• Следствие 2: H(A1…Ak) ≤ H(A1) + … + H(Ak).
• Следствие 3: H(A|BC) ≤ H(A|B).
21

22.

Взаимная информация
• Рассмотрим меру изменения количества информации,
содержащейся в исходе ai из A, при условии, что реализовался
исход bj из B.
p(
a
ib
j)
I(a
b
log
i,
j)
2
p(a
i)
• Это величина называется взаимной информацией исходов ai и bj.
22

23.

Взаимная информация
p(
a
b
) p(
a
b
)p(b
)
i
j
i
j
j
I(a
,
b
)
log
log
i
j
2
2
p(a
)
p(a
)p(b
)
i
i
j
p(a
b
p(a
i)p(
ja
i)
ib
j)
log
log
2
2
p(a
p(a
i)p(b
j)
i)p(b
j)
p(
b
ja
i)
log
I(b
2
j,a
i)
p(b
j)
23

24.

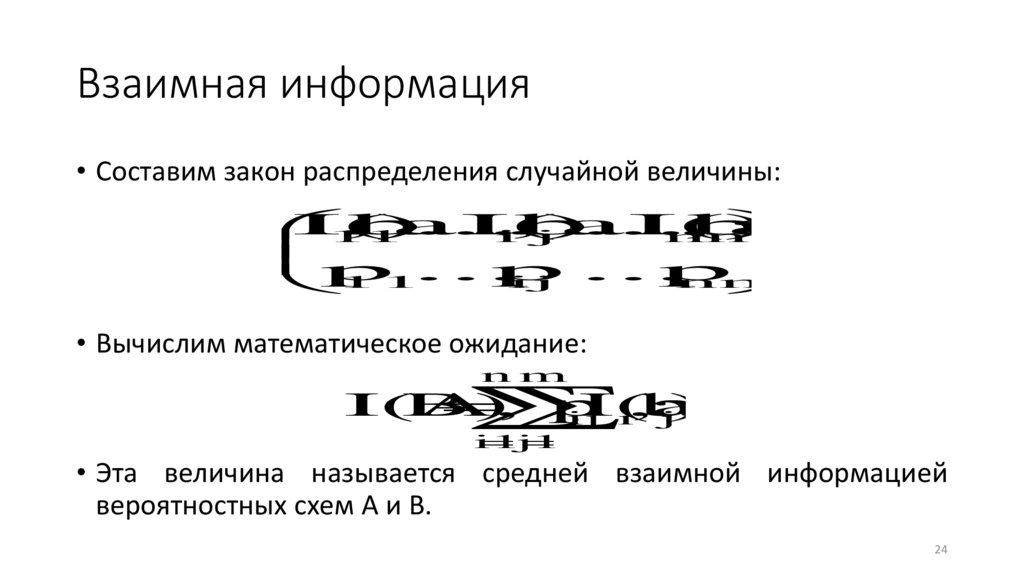
Взаимная информация
• Составим закон распределения случайной величины:
I(a
,
b
)...
I(a
,
b
)...
I(a
,
b
)
1
1
i
j
n
m
p ...
p
...
p
11
ij
nm
• Вычислим математическое ожидание:
nm
I(A,
B)
p
I(a
b
ij
i,
j)
i
1j
1
• Эта величина называется средней взаимной информацией
вероятностных схем A и B.
24

25.

Взаимная информация
n
m
n
m
i
1
j
1
i
1
j
1
I(A,
B)
p
I(a
,
b
)
p
I(b
,
a
)
I(B
A)
ij
i
j
ij
j
i
• Т.о. I(A,B) = I(B,A).
25

26.

Собственная информация
1
I(a
i) log
2
pi
• Эта
величина
называется
собственной
информацией,
содержащейся в исходе ai.
• Собственную информацию, содержащуюся в исходе ai,
интерпретируют как неопределённость события ai или как
количество информации, необходимое для разрешения этой
неопределённости.
26

27.

Собственная информация
• Составим закон распределения случайной величины:
I(a
)...
I(a
)...
I(a
)
1
i
n
p ...
p
...
p
i
n
1
• Вычислим математическое ожидание:
n
I(A)
p
iI(a
i)
i
1
• Эта величина называется средней собственной информацией
вероятностной схемы A.
27

28.

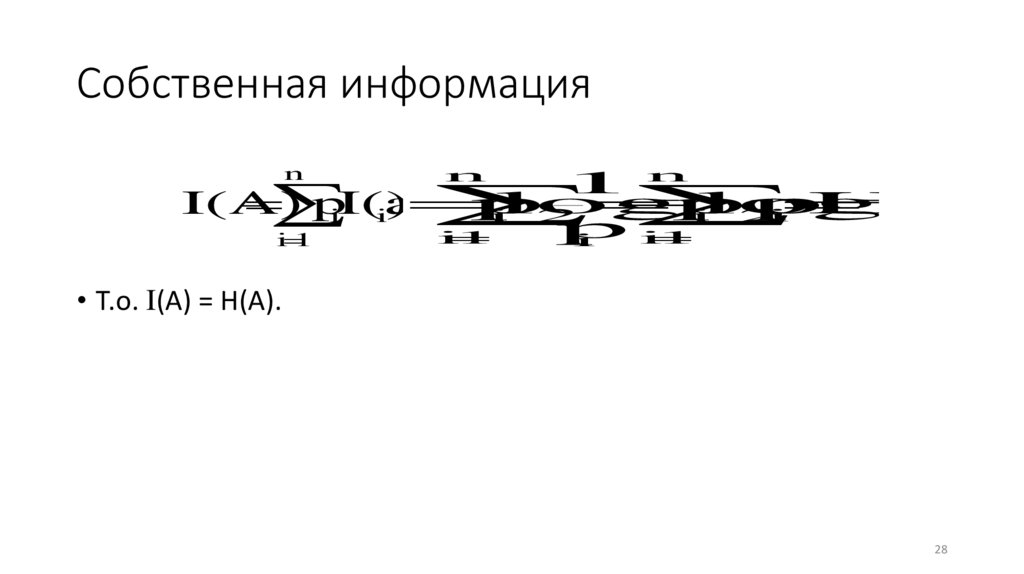
Собственная информация
n
n
1n
p
log
p
log
p
H(A
I(A)
p
i
2
i
2
i
iI(a
i)
p
i
1
i
1
i
1
i
• Т.о. I(A) = H(A).
28

29.

Условная собственная информация
1
I(
a
log
ib
j)
2
p(
a
ib
j)
• Эта величина называется условной собственной информацией,
содержащейся в исходе ai при условии реализации исхода bj.
29

30.

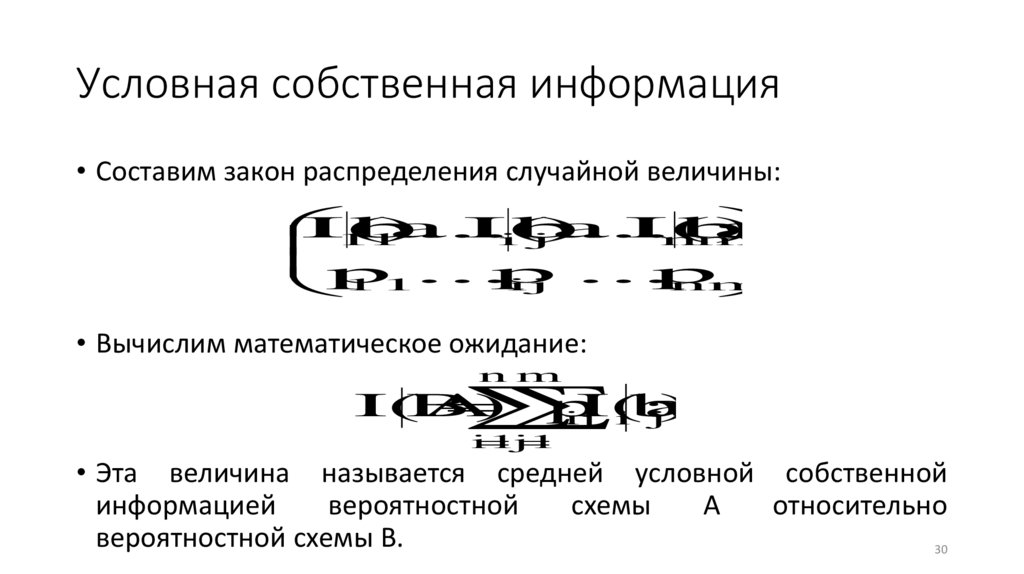
Условная собственная информация
• Составим закон распределения случайной величины:
I(a
b
)...
I(a
b
)...
I(a
b
)
1
1
i
j
n
m
p ...
p
...
p
ij
nm
11
• Вычислим математическое ожидание:
n m
I(A
B)
p
I(a
ij
ib
j)
i
1j
1
• Эта величина называется средней условной собственной
информацией
вероятностной
схемы
A
относительно
вероятностной схемы B.
30

31.

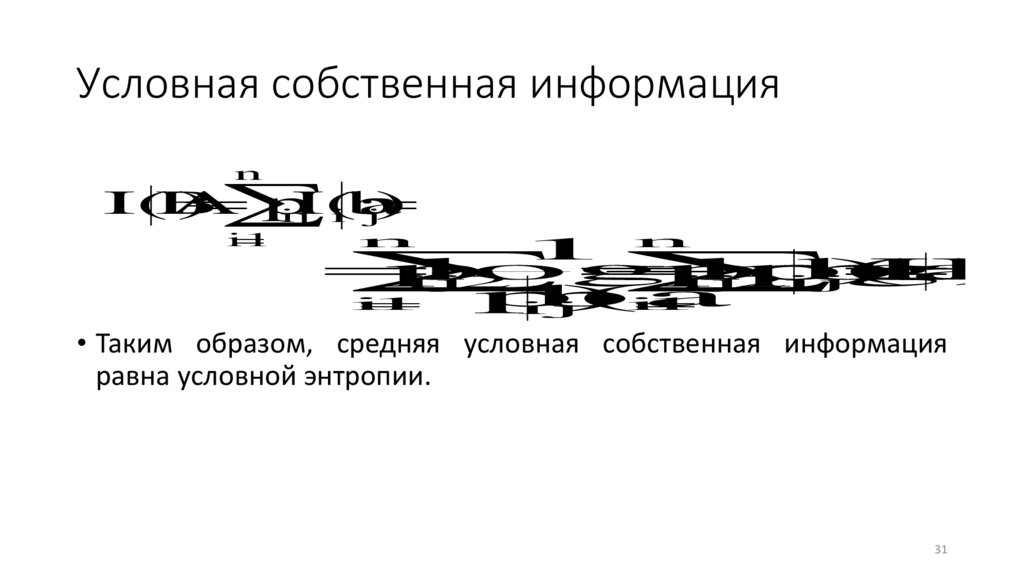
Условная собственная информация
n
I(A
B
)
p
I(a
ij
ib
j)
i
1
n
1 n
p
log
p
log
p(a
b
)
H(
B
)
ij
2
ij
2
i
j
p(a
b
)i
i
1
1
i
j
• Таким образом, средняя условная собственная информация
равна условной энтропии.
31

32.

Связь между видами информации
p(
a
b
)
i
j
I(a
,
b
)
log
log
p(
a
b
)
log
p(a
)
i
j
2
2
i
j
2
i
p(a
)
i
1
1
log
log
I(a
)
I(a
b
)
2
2
i
i
j
p(
a
b
) p(a
)
i
j
i
Аналогично
,
I(a
,
b
)
I(b
)
I(b
a
).
i
j
j
j
i
32

33.

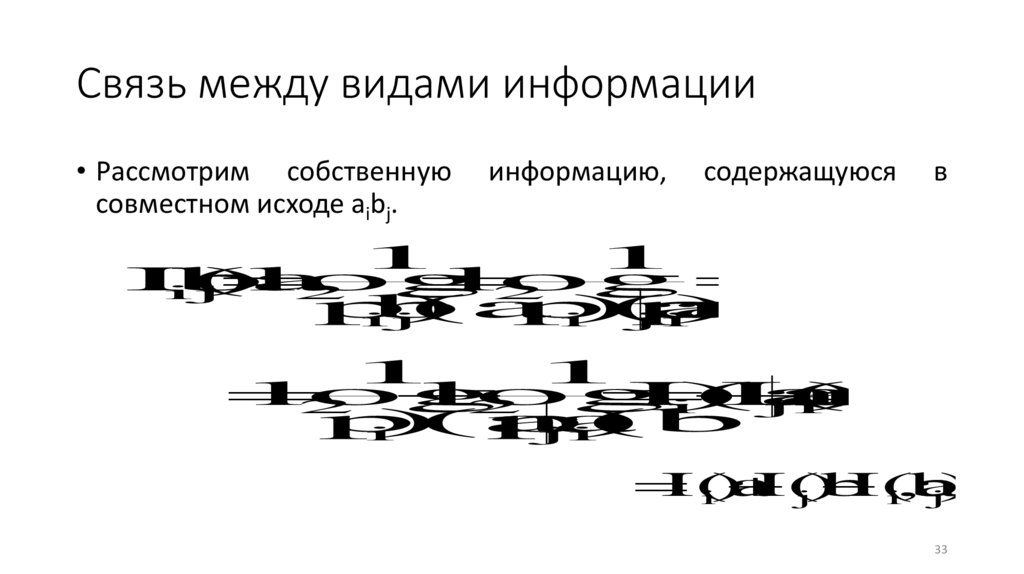
Связь между видами информации
• Рассмотрим собственную
совместном исходе aibj.
информацию,
содержащуюся
в
1
1
I(a
b
)
log
log
i
j
2
2
p(a
b
)
p(a
)p(b
a
)
i
j
i
j
i
1
1
log
log
I(a
)
I(b
a
)
2
2
i
j
i
p(a
) p(b
a
)
i
j
i
I(a
I(b
I(a
b
i)
j)
i,
j)
33

34.

Связь между видами информации
• Таким образом, I(aibj) = I(ai) + I(bj) ‒ I(ai,bj)
• Усредняя это выражение, получаем:
• H(AB) = H(A) + H(B) ‒ I(A,B)
• Отсюда: I(A,B) = H(A) + H(B) ‒ H(AB)
• I(A,B) = H(A) + H(B) ‒ H(A) ‒ H(B|A) = H(B) ‒ H(B|A)
• Так как H(B|A) ≤ H(B), следовательно I(A,B) ≥ 0.
34

35.

Свойство средней взаимной информации
• Теорема: Пусть A, B и C ‒ вероятностные схемы, ϕ: A C ‒
сюръективное отображение. Тогда I(A,B) ≥ I(C,B).
• Таким образом, средняя взаимная информация не увеличивается
при преобразовании схем.
• Равенство имеет место в том случае, если ϕ ‒ биекция.
35

36.

Непрерывные вероятностные схемы
• Пусть A ‒ непрерывная вероятностная схема. Тогда вероятностное
распределение задается функцией плотности распределения
вероятностей.
• Тогда энтропия схемы A:
H(A)
p(x)dx
2
p(x)log
36

37.

Непрерывные вероятностные схемы
• Пусть B – непрерывная вероятностная схема с плотностью
распределения q(y).
• Для объединенной вероятностной схемы AB существует
совместная плотность распределения вероятностей p(x,y).
• Энтропия объединенной непрерывной вероятностной схемы:
H(AB)
p(x,
y)log
p(x,
y)dxdy
2
37

38.

Непрерывные вероятностные схемы
• Частные распределения:
p
(
x
)
p(x,
y)dy
,q
(
y
)
p(x,
y)dx
• Условные распределения
p(xy)
p(xy)
p
(
x
y
)
,q
(
y
x
)
q(y) p(x)
38

39.

Ёмкость
• Максимальная энтропия системы равна
n
111
H
(A)
log
n
log
n
log
n
max
2
2
2
nnn
i
1
• Таким образом при равновероятных выборах формула энтропии
преобразуется в формулу Хартли.
• Hmax(A) называется ёмкостью системы A.
39

40.

Избыточность
• Абсолютной избыточностью называется величина
D
H
(A)
H(A)
max
• Относительной избыточностью называется величина
H
(A)
H(A)
max
D
отн
H
(A)
max
• Относительная избыточность показывает, насколько рационально
применяются символы данного алфавита.
40

41.

Дискретный источник сообщений
• Под дискретным источником сообщений будем понимать
устройство, порождающее последовательности, составленные из
букв конечного алфавита A = {a1, a2, …, an}. При этом буквы
последовательностей порождаются в дискретные моменты
времени.
• Любой непрерывны источник информации можно заменять с
заданной степенью точности некоторым дискретным источником.
41

42.

Дискретный источник сообщений
• Пусть ct1t2…tm(ai1ai2…aim) ‒ событие, заключающееся в том, что в
момент времени tj источник порождает символ aij.
• Для математического описания источника кроме алфавита нужно
также знать распределение вероятностей p(c) для событий
указанного выше вида.
42

43.

Стационарный источник сообщений
• Источник
сообщений
называется
стационарным,
если
p(ct1t2…tm(ai1ai2…aim)) = p(ct1+j t2+j…tm+j (ai1ai2…aim)) для любого j.
• Другими словами, источник стационарный, если вероятность
того, что источник порождает некоторую последовательность,
составленную из букв алфавита A, в моменты времени 1, 2, …, m,
равна вероятности того, что в точности такая же
последовательность порождается в моменты временя 1+k, 2+k, …,
m+k для любого k.
• Таким образом, стационарность означает неизменность во
времени всех конечномерных распределений.
43

44.

Энтропия источника
• Для стационарного источника множество всех событий
ct1t2…tm(ai1ai2…aim) можно рассматривать как вероятностную схему,
событиями которой являются всевозможные наборы символов
длины m.
• Для такой вероятностной схемы можно вычислить энтропию:
H(C
)
p(a
a
...a
)log
p(a
a
...a
).
m
i
i
i
2
i
i
i
12
m
12
m
• Здесь сумма берется по всевозможным наборам символов
алфавита A длины m.
44

45.

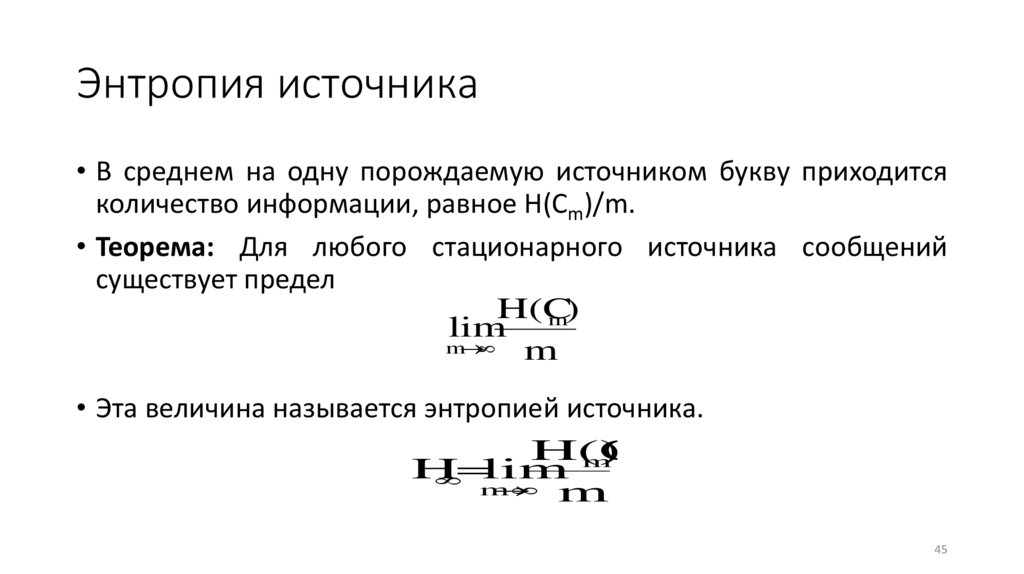
Энтропия источника
• В среднем на одну порождаемую источником букву приходится
количество информации, равное H(Cm)/m.
• Теорема: Для любого стационарного источника сообщений
существует предел
H(C
m)
lim
m
m
• Эта величина называется энтропией источника.
H(C
)
m
H
lim
m
m
45

46.

Энтропия источника
• Пусть источник порождает последовательности по схеме
независимых испытаний.
• Тогда H(Cm) = mH(C1) = mH(A).
• Следовательно, H∞ = H(A).
• Такие источники, для которых буквы, порожденные в
предыдущие моменты времени, не влияют на буквы,
порождаемые в последующие моменты времени, называются
источниками без памяти.
46

47.

Первая теорема Шеннона
• Первая теорема Шеннона: Рассмотрим источник без памяти,
имеющий энтропию H∞. Для любых чисел ε > 0 и η > 0 существует
число k0 такое, что при k > k0 все реализации источника длины k
могут быть разбиты на 2 класса: Ck = C’k U C’’k. Причем для любой
последовательности c’k из класса C’k имеет место условие:
1
1
log
H
η,
2
k p(c'
)
k
а суммарная вероятность последовательностей из класса C’’k
меньше ε.
47

48.

Первая теорема Шеннона
• Следствие 1: Вероятность p(c’k) можно оценить следующим
образом:
k(H
η)
k(H
η)
2
p(c'
)
2
.
k
• Следствие 2: Суммарная вероятность последовательностей из
класса C’k не менее 1 – ε.
48

49.

Вторая теорема Шеннона
• Вторая теорема Шеннона: Упорядочим все последовательности
длины k, полученные на источнике без памяти, по убыванию их
вероятностей. Выберем некоторое произвольное число 0 < α < 1.
Будем отбирать наиболее вероятные последовательности, пока
их суммарная вероятность не окажется такой, что добавление к
этой
сумме
вероятности
реализации
следующей
последовательности из упорядоченного списка сделает эту сумму
больше
α.
Множество
отобранных
таким
образом
высоковероятностных последовательностей обозначим Мk(α).
Имеет место следующее условие:
log
α
2M
k
lim
H
k
k
49

50.

Марковский источник
• Дискретный стационарный источник называется марковским
источником порядка m, если для любого k > m и любой
последовательности ai1ai2…aik выполняется условие:
p(aik|ai1ai2…aik-1) = p(aik|aik-maik-m+1…aik-1)
50