Similar presentations:
Теория информации (лекция 1)
1. Теория информации
Шлеймович Михаил Петрович2. Содержание
1. Информационные характеристикислучайных систем
2. Информационные характеристики каналов
связи
3. Кодирование информации
4. Сжатие информации
5. Помехоустойчивое кодирование
информации
6. Шифрование информации
3. Литература
1.2.
3.
4.
5.
6.
Ватолин, Д. Методы сжатия данных. Устройство
архиваторов, сжатие изображений и видео /Д. Ватолин, А.
Ратушняк, М. Смирнов, В. Юкин. – М.: ДИАЛОГ–МИФИ,
2002.
Вельшенбах, М. Криптография на Си и C++ в действии:
учебное пособие /М. Вельшенбах. – М.: Издательство
Триумф, 2004.
Вернер, М. Основы кодирования: учебник для ВУЗов
/М.Вернер. – М.: Техносфера, 2004.
Кудряшов, Б.Д. Теория информации: учебник для вузов /
Б.Д. Кудряшов. – СПб.: Питер, 2009.
Лидовский, В.В. Теория информации: учебное пособие
/В.В. Лидовский. – М.: Компания Спутник+, 2004.
Морелос-Сарагоса, Р. Искусство помехоустойчивого
кодирования. Методы, алгоритмы, применение / Р.
Морелос-Сарагоса. – М.: Техносфера, 2005.
4. Литература
Панасенко, С.П. Алгоритмы шифрования: специальныйсправочник /С.П. Панасенко. – СПб: БХВ-Петебург, 2009.
8. Панин, В.В. Основы теории информации. Учебное
пособие для вузов /В.В.Панин. – М.: БИНОМ,
Лаборатория знаний, 2011.
9. Смарт, Г. Криптография /Г. Смарт. – М.: Техносфера, 2005.
10. Сэломон, Д. Сжатие данных, изображений и звука /Д.
Сэлоион. – М.: Техносфера, 2004.
11. Умняшкин. С.В. Теоретические основы цифровой
обработки и представления сигналов: учебное пособие
/С.В. Умняшкин. – М.: ИД «ФОРУМ»: ИНФРА-М, 2008.
12. Яглом, А.М. Вероятность и информация /А.М. Яглом, И.М.
Яглом. Изд. 4-е, стереот. – М.: КомКнига, 2006.
7.
5. Информационные характеристики случайных систем
СистемаДискретная случайная система
Энтропия
Количество информации
Информационные характеристики
непрерывной случайной системы
6. Объем информации
1.
2.
3.
4.
5.
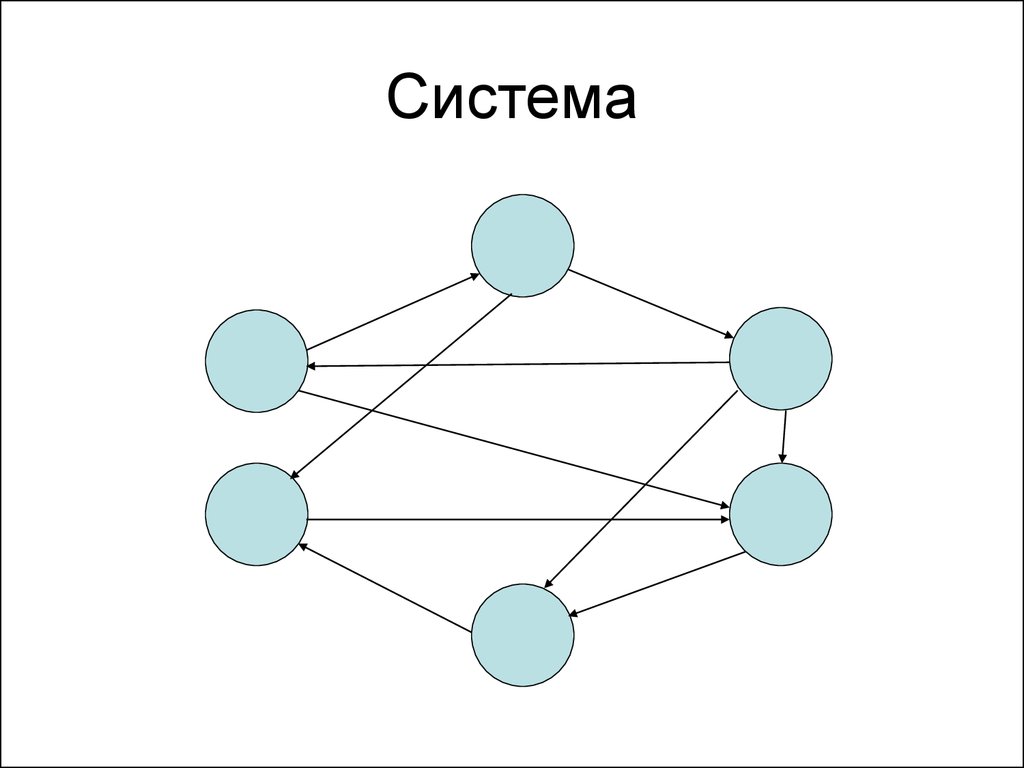
6. Система
7. Целостность системы
Система – это нечто большее, чемсовокупность ее частей.
8. Классификация систем по виду сигналов
СистемыНепрерывные
Дискретные
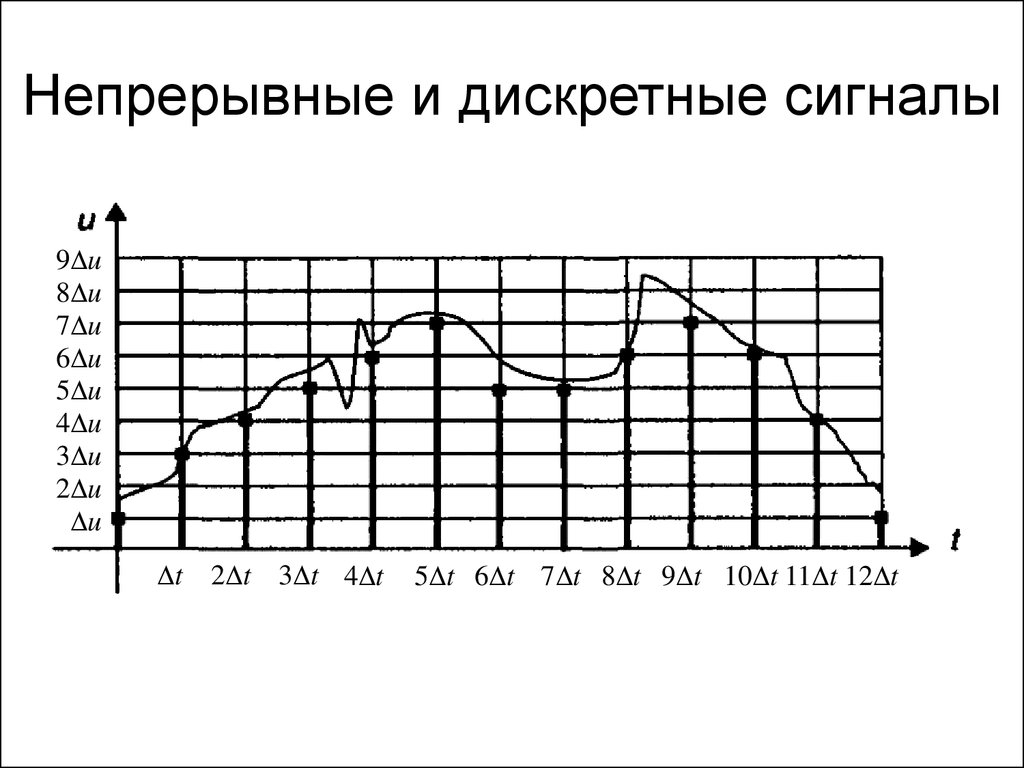
9. Непрерывные и дискретные сигналы
9 u8 u
7 u
6 u
5 u
4 u
3 u
2 u
u
t
2 t 3 t 4 t
5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 t
10. Классификация систем по определенности
СистемыДетерминированные
Случайные
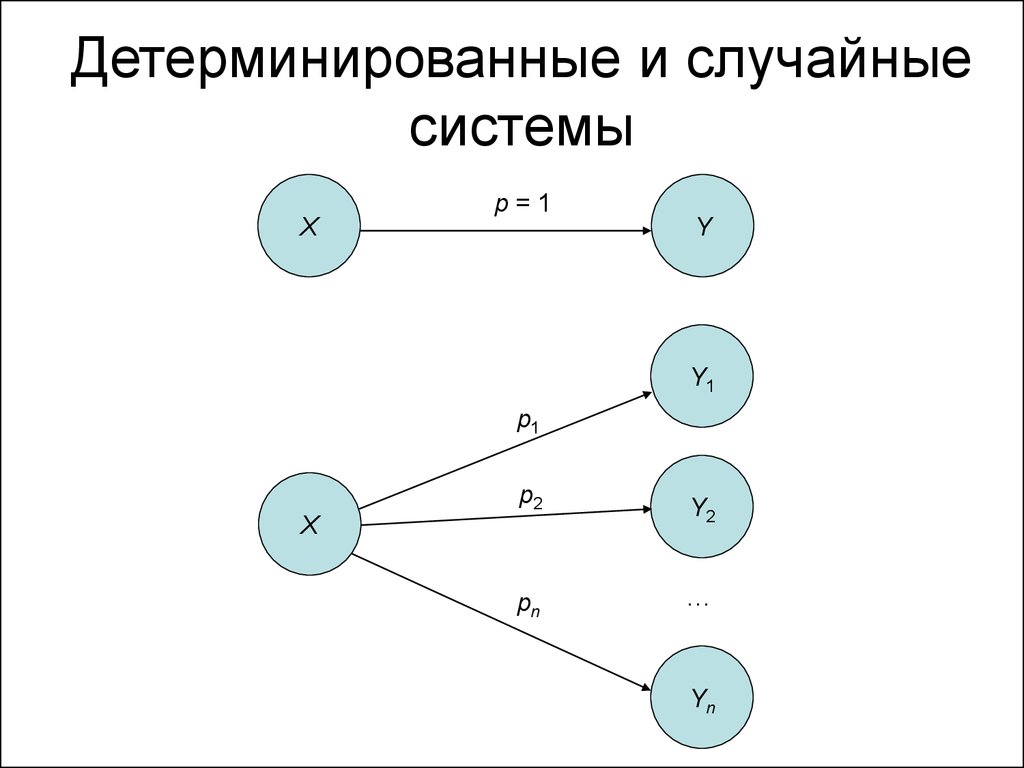
11. Детерминированные и случайные системы
Xp=1
Y
Y1
p1
p2
X
pn
Y2
…
Yn
12. Дискретная случайная система
X {x1 , x2 ,..., xn }P { p1 , p2 ,..., pn }
n
pi 1
i 1
13. Энтропия
1H ( xi ) H ( pi ) log
pi
1
H ( X ) H ( P ) M [log ]
pi
n
n
1
H ( X ) pi log pi log pi
pi
i 1
i 1
14. Основание логарифма
log a b c b a log d b c log d ac
log d b (log d a )(log a b) k1 log a b
log a b (log a d )(log d b) k2 log d b
15. Единица измерения энтропии
Двоичный логарифм: битНатуральный логарифм: нат
Десятичный логарифм: дит, харт, бан
16. Свойства энтропии
1. Энтропия – величина вещественная,ограниченная, неотрицательная
2. Система имеет максимальную
энтропию при равновероятном
распределении состояний
3. Система имеет минимальную
энтропию при наличии достоверного
состояния
17. Энтропия – величина вещественная и неотрицательная
n1
H ( X ) pi log
pi
i 1
i : 0 pi 1
1
1
pi 1 pi log 1 log 0
pi
1
1
pi 0 lim x log 0
H (X ) 0
x 0
x
1
0 pi 1 pi log 0
pi
18. Энтропия – величина ограниченная
ln x x 1n
1
H ( X ) pi ln
pi
i 1
n
1
n
1
pi 1 pi
pi
i 1
pi
i 1 pi i 1
n 1
H ( X ) n 1
n
19. Максимальное значение энтропии
ln x x 1n
n
1
1
H ( X ) ln n pi ln
ln n pi ln
pi
pi n
i 1
i 1
n
1
n
1
pi
1 pi
pi
i 1
pi n i 1 pi n i 1
1 1 0
H ( X ) ln n 0 H ( X ) ln n
n
20. Система с равномерным распределением вероятностей
1p1 p2 ... pn
n
n
n
1
1
1
H ( X ) ln
ln n
1 n i 1 n
i 1 n
1
n ln n ln n
n
H ( X ) ln n ln n max{ H ( X )}
21. Энтропия бинарной системы
X {x1 , x2 } {0,1}P { p1 , p2 } { p,1 p}
H ( X ) H ( P) H ( p)
1
1
p log (1 p ) log
p
1 p
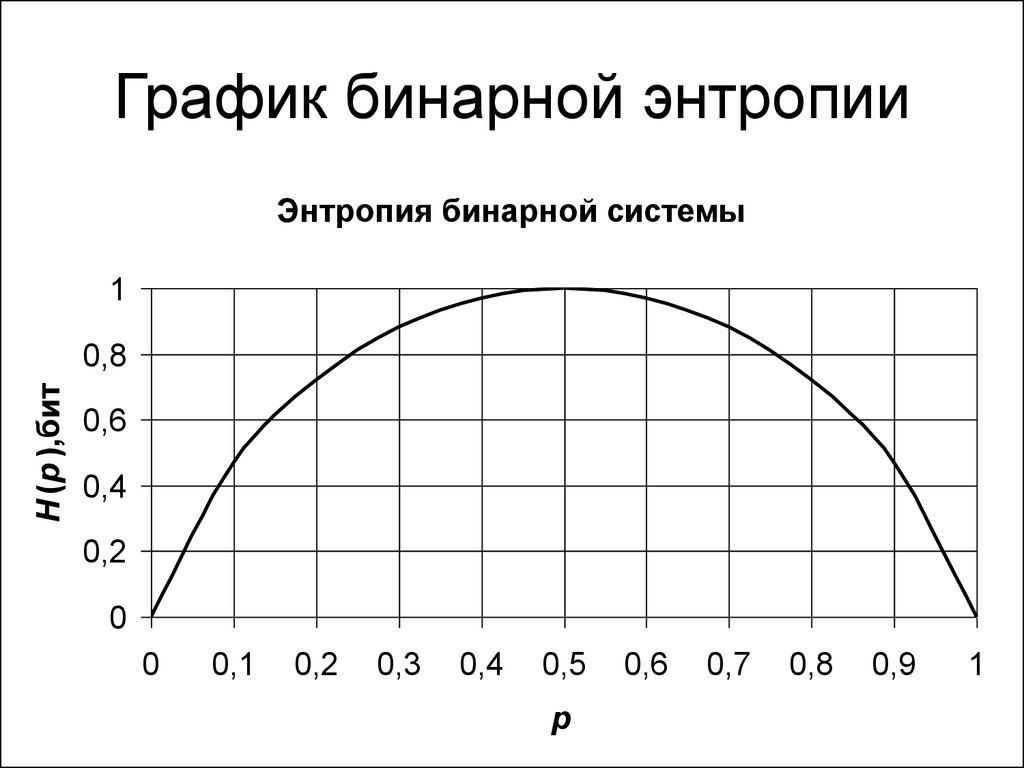
22. График бинарной энтропии
Энтропия бинарной системы1
H (p ),бит
0,8
0,6
0,4
0,2
0
0
0,1
0,2
0,3
0,4
0,5
p
0,6
0,7
0,8
0,9
1
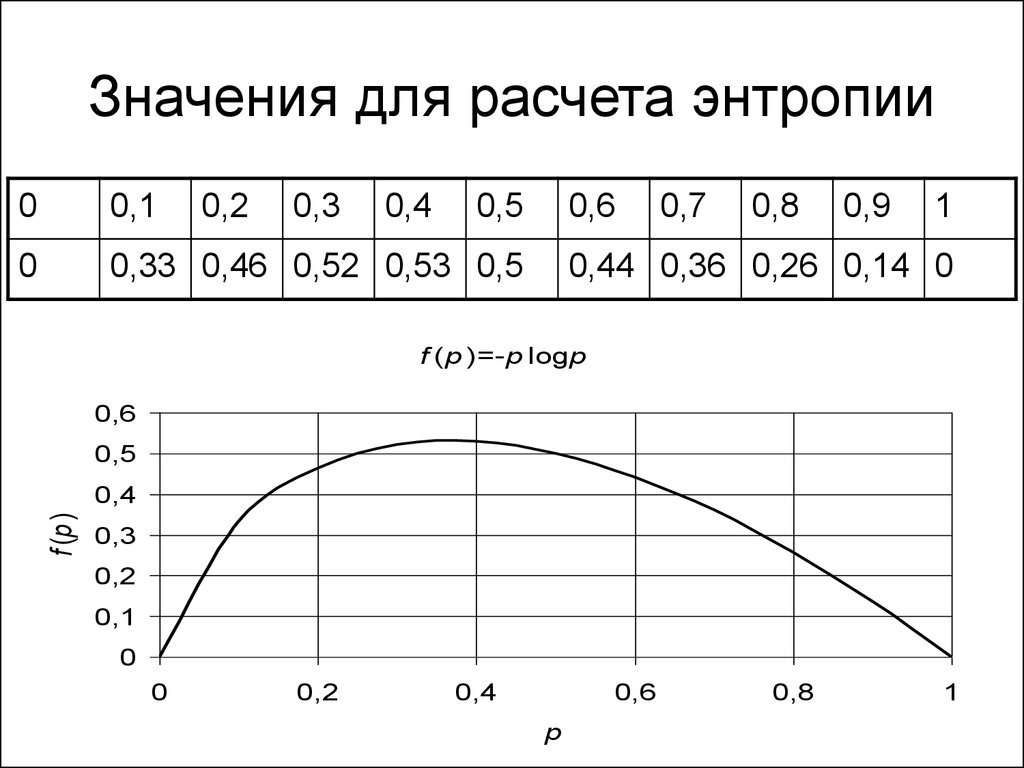
23. Значения для расчета энтропии
00,1
0,2
0,3
0,4
0,5
0
0,33 0,46 0,52 0,53 0,5
0,6
0,7
0,8
0,9
1
0,44 0,36 0,26 0,14 0
f (p )=-p logp
0,6
0,5
f (p )
0,4
0,3
0,2
0,1
0
0
0,2
0,4
0,6
p
0,8
1
24. Сложная система
XY
X
Y
X {x1 , x2 ,..., xn }, P( X ) { p( x1 ), p( x2 ),..., p( xn )}
Y { y1 , y2 ,..., ym }, P(Y ) { p( y1 ), p( y2 ),..., p( ym )}
( X , Y ) {( xi , y j )}, P( X , Y ) { p( xi , y j )
25. Энтропия сложной системы
nH ( X ) p( xi ) log p( x i )
i 1
m
H (Y ) p( yi ) log p( y j )
j 1
n m
H ( X , Y ) p( xi , y j ) log p( xi , y j )
i 1 j 1
26. Условная энтропия
p( x i , y j ) p( xi ) p ( y j / xi )p( x i , y j ) p( y j ) p ( xi / y j )
n
m
H ( X / Y ) p ( xi , y j ) log p ( xi / y j )
i 1 j 1
n
m
H (Y / X ) p ( xi , y j ) log p ( y j / xi )
i 1 j 1
H ( X / Y ) H ( X ), H (Y / X ) H (Y )
27. Энтропия объединения
H ( X , Y ) H ( X ) H (Y / X )H ( X , Y ) H (Y ) H ( X / Y )
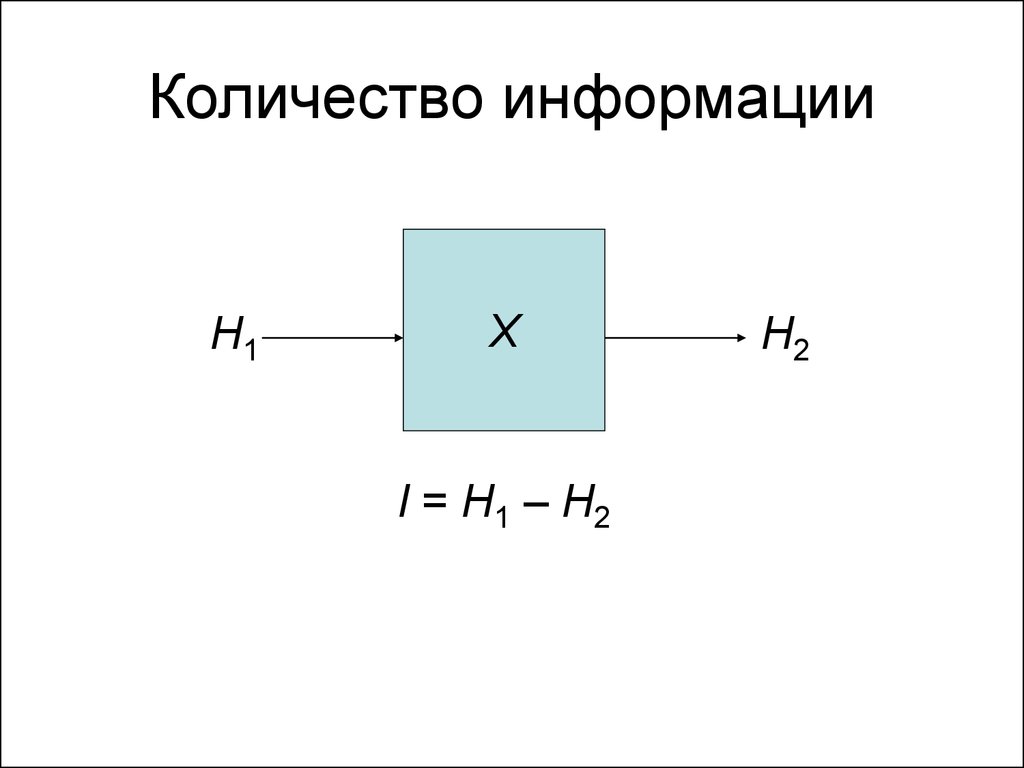
28. Количество информации
H1X
I = H1 – H2
H2
29. Количество информации по Хартли
S {s1 , s2 ,..., s N }si ai (1) ai ( 2 ) ...ai ( K )
K
ai ( k ) A {a1,a2 ,..., an }
n K
1
p( s1 ) p( s2 ) ... p( s N ) P
N
1
I ( si ) log log N
P
30. Количество информации по Шеннону
S {s1 , s2 ,..., s N }si ai (1) ai ( 2 ) ...ai ( K )
K
ai ( k ) A {a1,a2 ,..., an }
n K
n
p( si )
j 1
I ( si ) log
1
n
j 1
Kp j
pj
n
log
j 1
Kp j
pj
Kp j
pj
n
K ( p j log p j ) KH ( A)
j 1
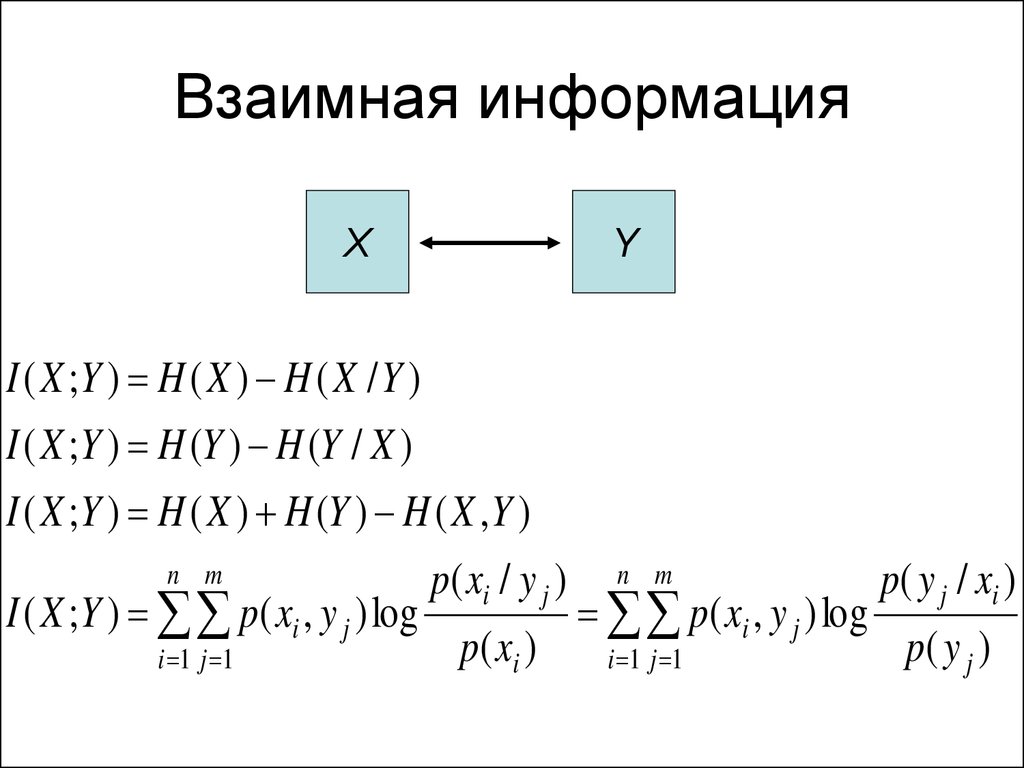
31. Взаимная информация
XY
I ( X ;Y ) H ( X ) H ( X / Y )
I ( X ;Y ) H (Y ) H (Y / X )
I ( X ;Y ) H ( X ) H (Y ) H ( X , Y )
n m
p( xi / y j )
i 1 j 1
p( xi )
I ( X ;Y ) p( xi , y j ) log
n m
p( y j / xi )
i 1 j 1
p( y j )
p( xi , y j ) log
32. Расчет взаимной информации
I ( X ;Y ) H ( X ) H (Y ) H ( X , Y )n
m
n m
i 1
j 1
i 1 j 1
p( xi ) log p( xi ) p( y j ) log p( y j ) p( xi , y j ) log p( xi , y j )
n m
n m
i 1 j 1
i 1 j 1
p( y j / xi ) p( xi ) log p( xi ) p( xi / y j ) p( y j ) log p( y j )
n m
p( y j ) p( xi / y j ) log{ p( y j ) p( xi / y j )}
i 1 j 1
n m
p( y j ) p( xi / y j )
i 1 j 1
p( xi ) p( y j )
p( xi , y j ) log
n m
p( xi / y j )
i 1 j 1
p( xi )
p( xi , y j ) log
n m
p( y j / xi )
i 1 j 1
p( y j )
p( xi , y j ) log
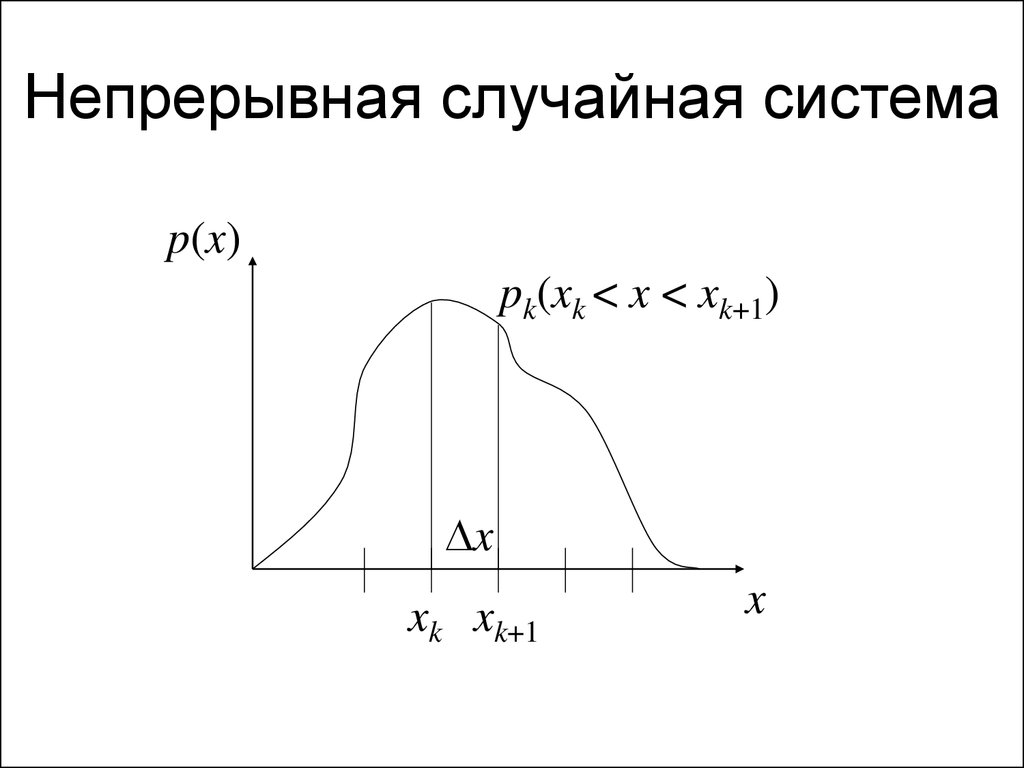
33. Непрерывная случайная система
p(x)pk(xk < x < xk+1)
x
xk xk+1
x
34. Информационные характеристики непрерывной случайной системы
pkxk x
p( x )dx p( x ) x
xk
n
H дискр ( X ) p( xk ) x log{ p( xk ) x}
k 1
n
n
k 1
k 1
p( xk ) x log p( xk ) p( xk ) x log x
H ( X ) lim H дискр ( X ) p( x ) log p( x )dx log x
x
H ( X ) H ( X ) log x
*
35. Объем информации
Q=klk – длина сообщения
l – длина кодовых слов для символов
сообщения

























 informatics
informatics








